灰色关联分位评价方法与多维相对贫困测度
2023-11-30谢玉梅
刘 震,谢玉梅,丁 松
(1.无锡学院 数字经济与管理学院,江苏 无锡 214105;2.江南大学 商学院,江苏 无锡 214122;3.浙江财经大学 经济学院,杭州 310018)
0 引言
关于贫困多维属性的论述最早出现于1998年诺贝尔经济学奖获得者阿马蒂亚·森的“自由发展”理论[1],该理论认为贫困的本质在于“可行能力”被剥夺,这种剥夺不仅体现为财富和收入,还包括教育、就业、医疗、政治权利等多个方面[2]。此后,多维贫困的概念逐渐在国际上达成共识,相关理论与方法的研究也逐渐受到重视。联合国开发计划署自2010 年开始定期发布全球多维贫困指数(MPI)[3]。在收入贫困与多维贫困的对比中,大量研究表明,收入只能反映贫困的一个方面,并不能充分反映收入之外其他维度的贫困[4,5]。还有一些学者重点关注了不同国家与地区的多维贫困特征及影响因素[6,7]。在国内,多维贫困理论也引起了广泛的探讨,但是大多围绕MPI 的基本框架展开[8—10]。
多维贫困理论提出后,学术界面临的最大挑战就是如何对多维贫困进行准确测度。目前,世界范围内的多维贫困测度方法大体可分为三类,分别是公理化方法、模糊集方法与信息理论方法[11]。这三类方法在精确性、实用性、可分解性、信息完整性等方面各有优劣。公理化方法是目前使用最为广泛的一类,其中以AF 方法(Alkire&Foster Counting Measurement)最为常见,该理论下的多维贫困指数具有可分解性[12,13]。模糊集方法采用隶属度函数的形式解决了贫困率临界值设定的难题[14]。信息理论方法最大程度地保证了信息的完整性[15]。这三类方法不同程度地推动了多维贫困理论的发展,但是也存在一些不足。一是针对相对贫困的研究尚不多见。现有多维贫困测度方法大多需要先行设定贫困临界值与最低贫困维度,这就导致这类方法只能用于识别绝对贫困,无法适应社会不断发展所带来的相对贫困问题。二是缺乏适应我国新时代特征的多维贫困标准。
灰色关联理论是一类重要的数据分析方法,其基本思想是利用线性插值将离散数据映射为连续折线,进而通过几何特征相似程度判别序列间的关系[16]。从最原始的邓氏关联[17],到考虑相似性和接近性的灰色关联[18],再到面板数据灰色关联[19,20],灰色关联理论已经积累了大量模型,相关性质也得到了广泛的验证[21,22]。由于灰色关联模型对数据间关系的描述不受统计特征约束,因此在目标识别[23]、经济分析[24]、绩效评价[25]等领域得到了广泛的应用。在贫困人口的多维信息集合中,灰色关联模型可以将贫困对象视为一个整体,在统一的时空维度下进行对比,避免临界值设定与最低贫困维度要求所带来的主观偏误,并且随着样本集合的演化,灰色关联模型可以实现对相对贫困人口的动态调整,在解决多维贫困测度中的相对贫困问题方面有良好的应用前景。
基于以上分析,本文尝试采用灰色关联理论构建一类新的可以解释相对贫困现象的多维贫困测度方法,并且立足中国国情对现有多维贫困框架进行优化。相对于现有研究成果,本文做了以下几个方面的工作:(1)优化灰色关联评价体系,延伸了针对测算结果的加总与分解方法,从广度与深度两个方面构建总体指数,并且根据指数的算术特征进行分解;(2)利用指标分位思想实现了具有相对贫困特征的多维贫困识别,通过整体化的信息集结方式避免人为设置双重临界值所带来的绝对化偏误;(3)以乡村振兴主要目标为基础构建符合现阶段中国基本国情的多维贫困指标体系,利用最新的中国家庭追踪调查(CFPS)2018年的调研数据对我国多维贫困进行测度,为全面推进乡村振兴、加快农业农村现代化提供理论依据。
1 基于灰色相对分位的多维贫困测度方法
多维贫困测度一般以家庭作为基本单位,需要先通过调查获得每个家庭在不同维度的取值,然后根据数值的大小识别家庭的总体贫困状况以及各个维度的贫困状况。区别于传统的多维贫困测度方法,灰色关联方法无需设定双重临界值(即贫困临界值与最低贫困维度)。因此本方法采用总体视角进行评估,优先进行信息集结,并且以各指标分位数为标准,形成针对相对贫困的动态识别能力。测度分为贫困识别、贫困加总与指数分解三个步骤。
1.1 贫困识别
定义被测主体在各维度的取值。设Yn,d为n×d矩阵,令矩阵元素y∈Yn,d,yij表示家庭i在维度j上的取值,其中i=1,2,…,n;j=1,2,…,d,则称Yn,d为多维贫困矩阵,yij为多维贫困元素。行向量yi=(yi1,yi2,…,yid)表示第i个主体在所有维度的取值,列向量yj=(yi1,yi2,…,yid)T表示第j个维度所有被测主体的取值。
在灰色关联模型中,由于数据的数量级可能会对结果产生影响,因此建模前需要对数据进行初始化处理。为了避免极值对结果产生影响,本文采用均值化算子。设为初始化后的多维贫困元素,则:
初始化后,利用各维度的最小值构建极端贫困向量:
分别计算各被测主体与极端贫困向量之间的灰色关联度:
需要说明的是,灰色关联模型主要通过序列间的几何特征差异判别序列间的关系。本文将被测主体与极端贫困向量均映射为空间向量,进而通过度量空间向量之间的距离对被测主体的多维贫困状态进行排序,空间距离越小表明被测主体距离极端贫困向量越近,灰色关联度越大代表多维贫困程度越深。
参考式(2)的基本形式,计算基准向量与极端贫困向量之间的灰色关联度作为多维贫困识别标准,如表1 所示。在识别标准划分出的区间中,被测主体具有不同的多维贫困特征。当关联度大于10%分位数标准时,多维贫困状况最为恶劣。当关联度处于10%至25%分位数标准之间时,可认定为一般多维贫困。依次类推,当关联度小于90%分位数标准时,被测主体的多维贫困情况最优。一般情况下,可将25%分位数作为多维贫困识别标准,此时高于25%分位数标准的灰色关联度均被识别为多维贫困,即等级Ⅰ和等级Ⅱ为多维贫困人口。当然根据实际需要也可以适当降低或提高这一识别标准。
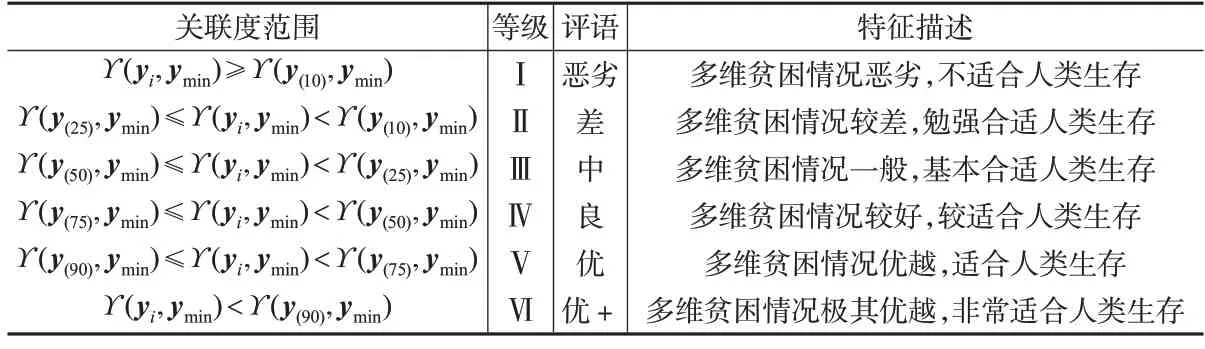
表1 多维贫困的灰色关联识别标准
1.2 贫困加总
为了进行更加深入的分析,多维贫困识别之后继续进行贫困加总,构建多维贫困指数。最简单的多维贫困指数是按贫困人口占总人口的比例计算的贫困发生率。设多维贫困发生率为H,被测贫困主体个数为n,识别的贫困主体个数为q(一般指贫困等级为Ⅰ与Ⅱ的贫困人口数),则:
这种贫困发生率的计算方法最大的优点是简单明了,但是缺点也非常明显,就是不能体现多维贫困的分布与深度。
为了解决这一问题,继续构建多维贫困分布指数。对多维贫困被测主体进行重新排序,设y1,y2,…,yq为多维贫困主体,yq+1,yq+2,…,yn为非贫困主体,第i个贫困主体的贫困维度总数为ci,i=1,2,…,q,平均贫困份额,多维贫困分布指数为M0,则:
式(5)的多维贫困分布指数M0由两个部分构成,一是贫困发生率H,二是平均贫困份额A,因此多维贫困分布指数M0体现了多维贫困的分布广度。其中:
其中,cij为多维贫困主体i在维度j下的贫困识别结果,当该主体在该维度下贫困时赋值为1,当该主体在该维度下非贫困时赋值为0。若以25%分位数为判别标准,则有:
为了更加深入地分析多维贫困情况,继续构建多维贫困深度指数。设多维贫困主体i在维度j下的贫困深度为sij,平均贫困距G=,多维贫困深度指数为M1,则:
式(8)体现了多维贫困的总体深度,其中,sij为主体i在维度j下的取值与分位数标准距离的比值,若主体i在维度j下非贫困,则sij赋值为0,由此可知0 ≤sij≤1。仍然以25%分位数标准为例,有公式:
1.3 指数分解
由于贫困发生率、多维贫困分布指数与多维贫困深度指数本质上都是不同标准下贫困水平的算术平均值,因此这三类多维贫困指数均可以按照维度、地区、省份等不同划分进行分解。假设多维贫困指数为M,维贫困矩阵Y可划分为城镇与农村两组,用u表示城镇的多维贫困矩阵,v表示农村的多维贫困矩阵,M(u),M(v)分别为城镇子集和农村子集的多维贫困指数,n(Y)、n(u)、n(v)分别表示不同多维贫困指数的算数平均基数,则有:
式(10)是多维贫困指数M的分解,说明多维贫困指数可以表示为子矩阵贫困指数的加总。这里的M可以表示贫困发生率,也可以代表多维贫困分布指数或多维贫困深度指数。分解的标准并不局限于城镇与农村,根据子矩阵的不同划分,还可以对维度、地区、省份等进行分解。分解后数值占总指数的比重表示子集的贡献率,贡献率之和等于1。以式(10)为例,设城镇贡献率为ϕu,农村贡献率为ϕv,根据定义可知ϕu+ϕv=1,则有:
2 多维贫困的测度与分解
2.1 数据来源与测度框架
本文数据来自北京大学中国社会科学调查中心(ISSS)开展的中国家庭追踪调查(CFPS)。为了保证结果的有效性,采用CFPS调查中最新的2018年的数据集。在数据处理方面,以家庭为单位,按照无缺失值且有明确回答为标准进行样本筛选,最终得到有效样本12605 个,分布在我国31个省份(不含港澳台),如表2所示。
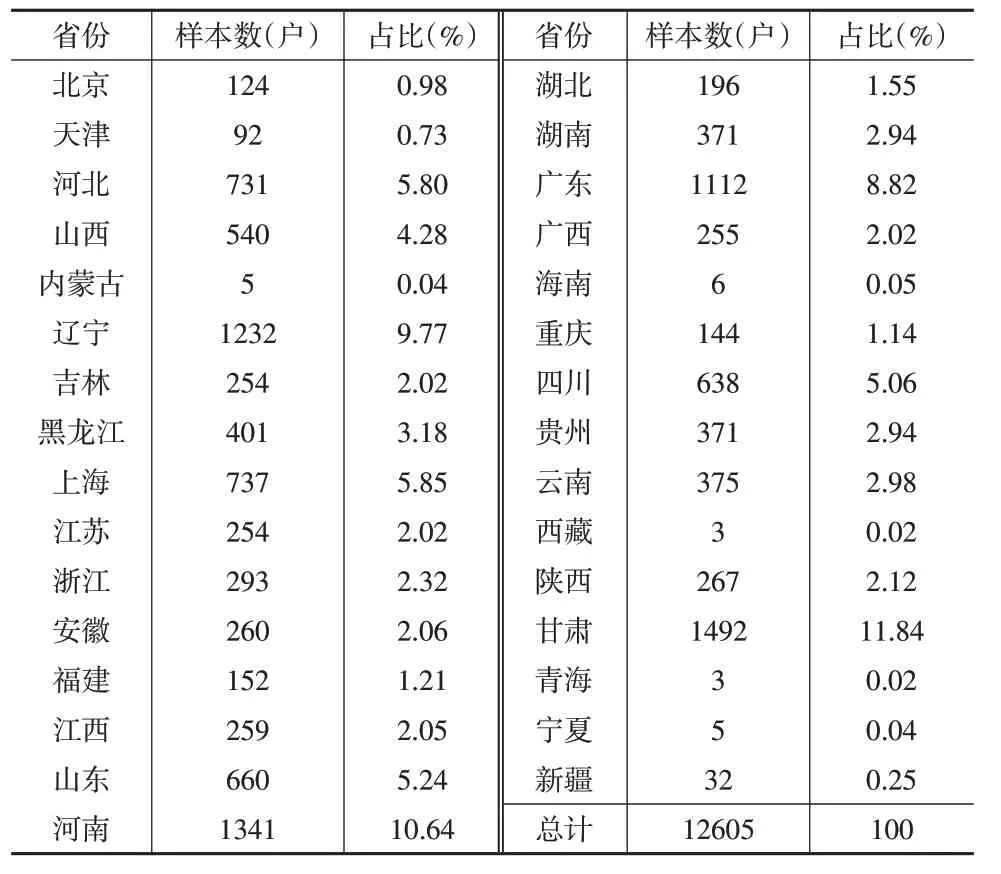
表2 样本分布情况
根据中国基本国情与调查数据结构优化多维贫困指标体系,以家庭为测度单位,综合考虑家庭内部各成员的总体情况。为了体现中国的实际情况,以《中国农村扶贫开发纲要(2011—2020 年)》为贫困维度与指标设定的主要依据,结合国内外现有研究以及数据的可获取性,得到多维贫困指标体系,如表3 所示。在权重方面,本文选择最常用的双重等权重计算方法,六个维度各占1/6,每个维度中,各指标也拥有相同的权重。
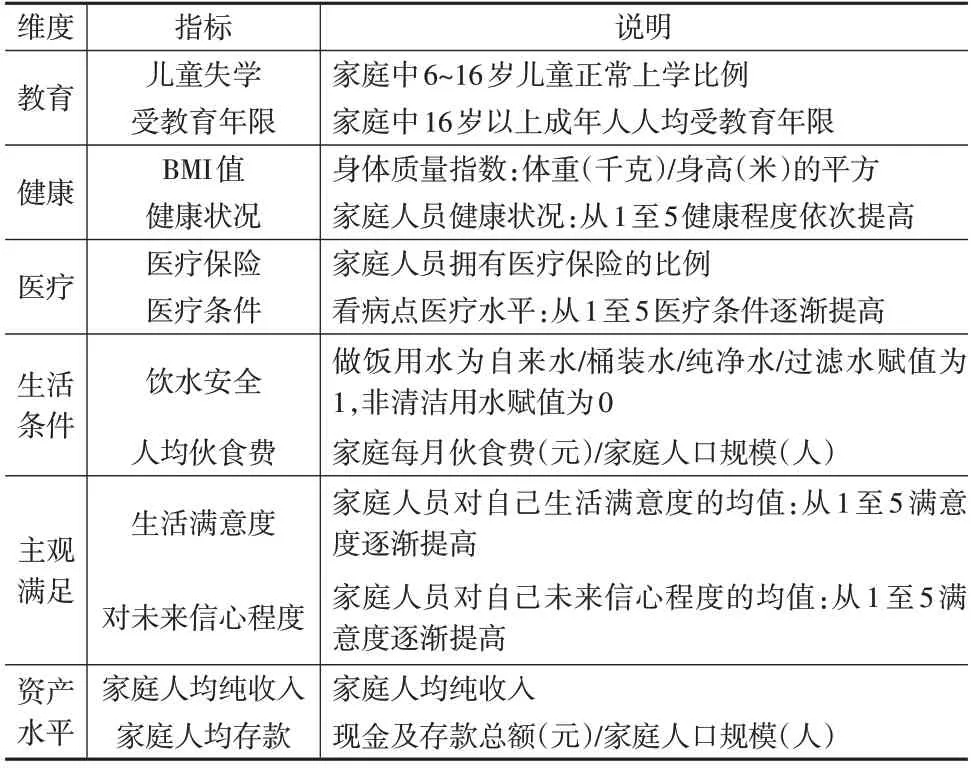
表3 多维贫困指标体系
2.2 单维贫困识别
关注多维贫困指标体系中各维度的单独贫困情况,计算贫困主体与极端贫困向量在各维度下的贫困距,六个维度的贫困距的核密度曲线如图1所示。需要说明的是,由于生活条件和资产水平维度最高值与最低值差距极大,因此图1 只展示了这两个维度贫困距在10 以下的核密度图。从图1中可以发现,教育、健康、生活条件和资产水平四个维度的核密度曲线偏向左侧,这说明在这四个维度下被测主体更多在低层次聚集。医疗和主观满足维度的核密度曲线偏右,这说明被测主体在这两个维度下更多在高层次聚集。
分别以各指标的10%、25%和50%分位数为标准,从全国、城镇和农村三个视角进行贫困识别,结果如表4 所示。可以发现,10%分位数标准下的贫困发生率最低,50%分位数标准下的贫困发生率最高,这是由于分位数越大表示贫困识别的标准越宽泛,因此纳入贫困的人口也就越多。在贫困维度方面,健康与主观满足两个维度的贫困状况最为严重,在10%分位数标准下贫困发生率分别为70.74%和46.16%,在25%分位数标准下贫困发生率分别为90.28%和78.45%,在50%分位数标准下更是分别达到了96.13%和86.16%。教育维度的贫困状况也不乐观,在三类分位数标准下的贫困发生率分别为11.50%、25.68%和50.56%。在城乡差异方面,城镇人口在教育、生活条件、资产水平维度的贫困发生率远低于农村人口,但是在健康、医疗、主观满足维度的贫困发生率高于农村人口,体现了城镇与农村贫困特征的不同。
2.3 多维贫困识别
利用中国家庭追踪调查(CFPS)2018年的数据集测度我国的多维贫困情况。根据前文介绍的方法,分别计算各贫困主体与极端贫困之间的灰色关联度,同时计算各指标分位数与极端贫困之间的关联度。可以得到,10%分位数标准为0.40。25%分位数标准为0.29,50%分位数标准为0.26,75%分位数标准为0.22,90%分位数标准为0.16。根据这些标准进行贫困等级划分,当被测主体的灰色关联度大于0.40 时,多维贫困等级为Ⅰ级;当灰色关联度介于0.29 与0.40 之间时,多维贫困等级为Ⅱ级;当灰色关联度介于0.26与0.29之间时,多维贫困等级为Ⅲ级;依此类推,可以得到多维贫困Ⅳ级、Ⅴ级和Ⅵ级的关联度区间。灰色关联度的核密度曲线与贫困划分标准如图2(a)所示,多维贫困识别结果的分布情况如图2(b)所示。
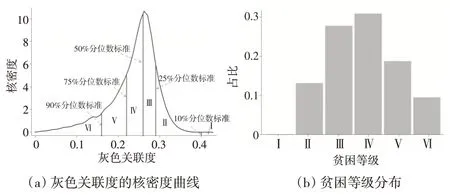
图2 基于灰色关联模型的多维贫困估计结果
利用多维贫困识别结果估算三类多维贫困指数,如表5所示。在10%分位数标准下,仅有等级Ⅰ被识别为贫困;在25%分位数标准下,贫困等级Ⅰ和Ⅱ被纳入贫困识别范围;在50%分位数标准下,等级Ⅰ、Ⅱ、Ⅲ均被纳入贫困识别范围。分位数增加代表贫困识别的范围逐渐扩大,因此分位数增加必然伴随着较高的贫困发生率。表5 验证了这一结论,我国10%分位数标准下的贫困发生率(H)为0.02%,25%分位数标准下的贫困发生率(H)为13.17%,50%分位数标准下的贫困发生率(H)为40.94%。为了在更加合理的范围内分析我国的相对贫困问题,后文主要以25%分位数标准下的结果作为分析对象。
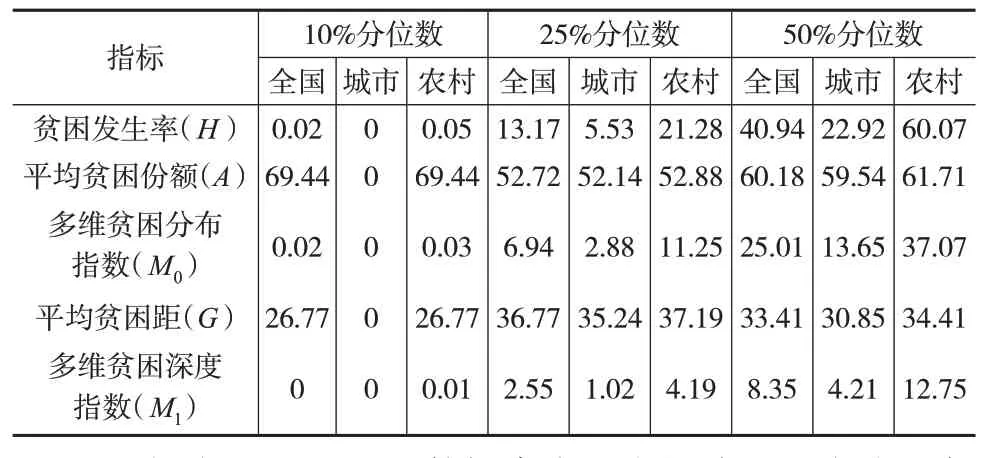
表5 中国城乡多维贫困估计结果(单位:%)
继续利用CFPS2018数据库中的省级编码测度我国各区域的多维贫困情况,分为华东(包括山东、江苏、安徽、浙江、福建、上海)、华南(包括广东、广西、海南)、华中(包括湖北、湖南、河南、江西)、华北(包括北京、天津、河北、山西、内蒙古)、西北(包括宁夏、新疆、青海、陕西、甘肃)、西南(包括四川、云南、贵州、西藏、重庆)、东北(包括辽宁、吉林、黑龙江)七个地区,25%分位数标准下的测算结果如下页表6所示。可以发现,贫困发生率(H)在华南和西南地区最高,在华东地区最低。平均贫困份额(A)在全国范围内的差距不大。但是平均贫困距(G)在华东地区最高,在西南地区最低。
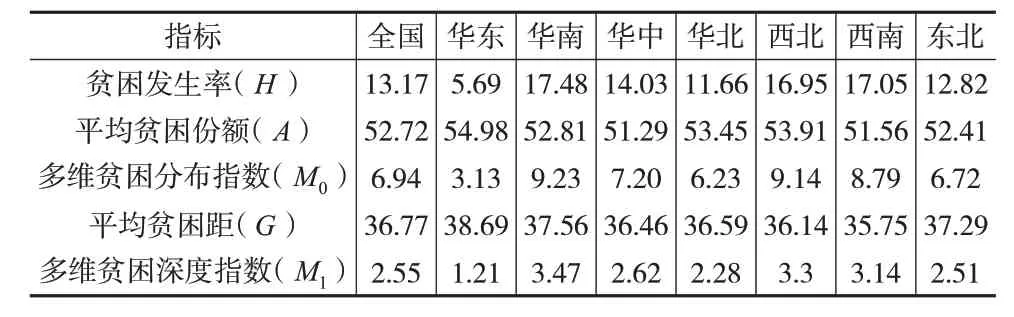
表6 中国多维贫困指数分区域测度结果(25%分位数标准,单位:%)
2.4 多维贫困指数分解
为了进一步分析三类多维贫困指数产生的原因,表7展示了不同标准下多维贫困发生率按照城乡与区域分解的结果。先关注城镇与农村的角度,在10%分位数标准下,农村的贡献率为100%,城镇的贡献率为0;在25%分位数标准下,农村的贡献率为78.37%%,城镇的贡献率为21.63%;在50%分位数标准下,农村的贡献率为71.16%,城镇的贡献率为28.84%,可以发现农村对于多维贫困指数的贡献率远高于城镇。再从区域角度对多维贫困发生率进行分解,在10%分位数标准下,东北地区的贡献率最高,为66.67%;在25%分位数标准下,华中和西北地区的贡献率最高,分别为18.31%和18.37%;在50%分位数标准下,仍然是华中和西北地区的贡献率最高,分别为17.81%和19.24%。相对而言,华东地区贡献率在不同分位数标准下均为最低。
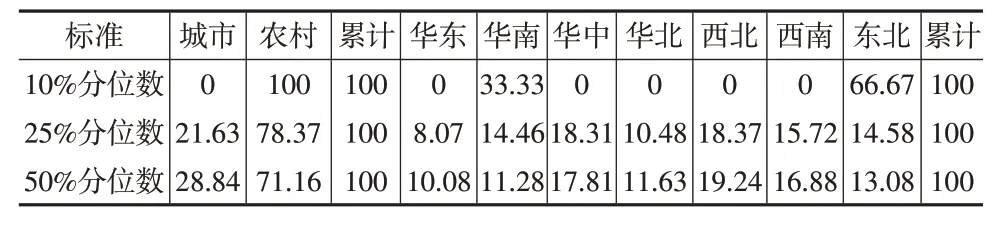
表7 中国多维贫困发生率的城乡与区域分解(单位:%)
在25%分位数标准下对多维贫困分布指数进行分解,分别得到城乡、区域和贫困维度三个视角下的分解结果,如表8 所示。在城乡视角下,城镇贡献率为21.39%,农村贡献率为78.61%,这说明农村贫困人口的贫困维度数占比远高于城镇,与贫困发生率的分解结果基本一致。在区域视角下,仍然是华中和西北地区的贡献率最高,分别为17.82%和18.79%,华东地区的贡献率最低,为8.42%。在贫困维度的视角下,教育维度的贡献率最高,这与之前单维贫困的测度结果有较大差距,这说明教育贫困虽然在总人口中出现频率不高,但是在贫困人口中教育贫困的分布是非常广泛的。医疗维度的贡献率最低,这与之前单维贫困的测度结果又有较大的差距,这说明医疗贫困虽然在总人口中占比较高,但是相对而言,我国医疗资源的分布基本能够满足绝大部分地区的需求,贫困人口的医疗需求能够得到基本保障。

表8 中国多维贫困分布指数的分解(25%分位数标准,单位:%)
在25%分位数标准下,中国多维贫困深度指数的分解结果如表9 所示,分解仍然从城乡、区域和贫困维度三个视角展开。在城乡视角下,城镇的贡献率为20.50%,农村的贡献率为79.50%。在区域视角下,华中和西北地区的贡献率最高,分别为17.67%和18.46%,华东地区的贡献率最低,为8.86%。在贫困维度的视角下,生活条件维度的贡献率最高,达到了44.24%,这说明贫困人口在生活条件方面距离脱贫还有很大的差距。健康、医疗和主观满足三个维度的贡献率较低,分别为8.65%、8.72%和7.80%。
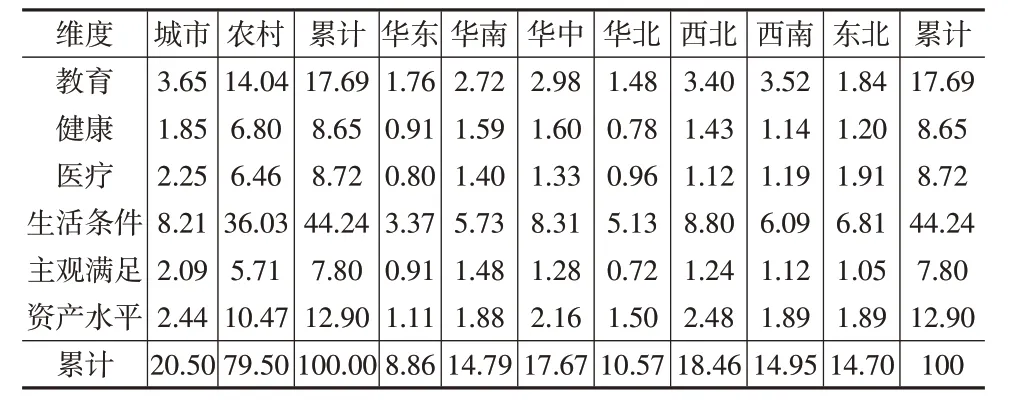
表9 中国多维贫困深度指数的分解(25%分位数标准,单位:%)
3 结论
在消除绝对贫困后,我国依然面临着相对贫困问题。为了加强对易返贫致贫人口的监测,本文从多维视角讨论相对贫困问题,基于灰色关联理论构建了一类新的多维贫困测度方法。该方法采用整体的视角进行信息整合,以分位数的视角设定具有动态特征的相对评价标准,避免了双重临界值设定所带来的主观偏误,提升了多维贫困识别的准确性。在理论层面拓展了灰色关联评价体系,建立了测度结果的加总与分解过程。在应用层面实现了具有相对贫困特征的多维贫困识别,验证了模型的有效性与实用性。主要结论如下:
(1)中国的城镇与农村都存在着多维贫困现象,若以全部指标的25%分位数作为标准,则全国的多维贫困发生率为13.17%,相应的城镇与农村的多维贫困发生率分别为5.53%和21.28%,农村的多维贫困发生率远高于城镇,但是在平均贫困份额和平均贫困距两个指标中,农村与城镇基本持平。
(2)华东地区的多维贫困发生率最低,为5.69%,华南、西北和西南地区的多维贫困发生率较高,分别为17.48%、16.95%和17.05%,华中、华北和东北地区的多维贫困发生率基本与全国持平。在平均贫困份额和平均贫困距两个指标中,全国各区域的水平基本相当。
(3)在单维贫困方面,健康、医疗和主观满足维度的单维贫困现象较为严重,但是这些并不是多维贫困的主要诱因。在多维贫困分布指数中,各维度的贡献率由高到低分别是教育、生活条件、资产水平、医疗、健康、主观满足。在多维贫困深度指数中,生活条件的贡献率远远高于其他维度。
