基于椭圆曲线的高效无证书环签名方案

朱秀萍，刘亚丽*，林昌露，李涛，董永权

基于椭圆曲线的高效无证书环签名方案

朱秀萍1，2，3，刘亚丽1，2，3*，林昌露2，李涛1，2，3，董永权1

（1.江苏师范大学 计算机科学与技术学院，江苏 徐州 221116； 2.福建省网络安全与密码技术重点实验室（福建师范大学），福州 350117； 3.广西密码学与信息安全重点实验室（桂林电子科技大学），广西 桂林 541004）（ ∗ 通信作者电子邮箱liuyali@jsnu.edu.cn）

环签名具有自发性和匿名性，被广泛用于解决用户身份和数据隐私泄露问题；而无证书公钥密码体制不仅可以解决密钥托管问题，还不需要公钥证书的管理；无证书环签名则结合了上述两者的优点，具有广泛的研究意义，但现有大多数无证书环签名方案基于双线性配对运算和模指数运算，计算成本高、效率低。为了提高签名阶段和验证阶段的效率，提出一种新的基于椭圆曲线的高效无证书环签名（ECL-RS）方案，使用了计算代价低、安全性高、灵活性好的椭圆曲线。该方案的安全性规约为离散对数困难问题和Diffie-Hellman问题，且在随机预言机模型（ROM）下证明了它能够抵抗公钥替换攻击和恶意密钥生成中心攻击，具有不可伪造性和匿名性。性能分析表明，ECL-RS方案只需（+2）（表示为环成员个数）次椭圆曲线标量乘法和标量加法运算，以及（+3）次单向哈希运算，在保证安全的情况下具有较低的计算代价和更高的效率。

环签名；椭圆曲线；无证书环签名；高效性；随机预言机模型

0 引言

环签名在2001年由Rivest等［1］首次提出，因按照一定规律首尾相连组成一个环状结构而得名。在环签名方案中，签名者可以任意选择几个成员组成一个环，没有群的建立过程，也没有群管理者，在没有其他环成员帮助的情况下生成签名。验证者使用公钥验证生成的签名是否由环中成员所产生，但是却无法确定签名是由环中哪个成员所产生。环签名有两个独特的性质：自发性和匿名性［1］。自发性允许签名者在没有任何其他小组成员的帮助或合作的情况下生成一个环签名；匿名性意味着环签名可以在不暴露实际签名者身份的情况下被验证。因此，环签名独有的自发性、匿名性以及灵活的结构等特性被广泛用于解决用户身份和数据隐私保护问题。

1976年，Diffie和Hellman［2］第一次提出了公钥密码学（Public Key Cryptography， PKC）的概念。传统的公钥基础设施（Public Key Infrastructure， PKI）［3］需要一个受信任的第三方证书颁发机构为每个用户颁发一个绑定用户身份和公钥的证书。Shim［4］提出了一个只需常数个双线性配对操作的环签名方案，在co-Diffifie-Hellman假设下，使用随机预言机模型（Random Oracle Model， ROM）证明了方案的安全性，并选择Barreto-Naehrig曲线上的最优配对来研究方案的性能；但方案需要证书管理开销和高计算代价的双线性配对，导致效率并不理想。张文芳等［5］提出了一个基于大整数分解难题和RSA公钥密码体制的环签名方案。该方案通过随机选择参数生成关联标签，使方案满足强匿名性，并在一定条件下可转换成普通数字签名。但在传统PKI的签名方案中，成员证书的传输和验证涉及相当多的通信和计算成本，因此效率低。从上述分析可以得出传统PKI不仅效率低还会带来证书管理问题，因为验证者必须检查每个用户证书的有效性，证书的管理在计算时间和存储空间方面要求非常高，使得签名方案复杂且效率低。

为了解决证书管理问题，Shamir［6］在1984年引入了基于身份的公钥密码学（IDentity Based-Public Key Cryptography， IDB-PKC）。在IDB-PKC中，所有用户的私钥都是由一个被称为私钥生成器（Private-Key Generator， PKG）的可信第三方产生。Wang等［7］提出了一种新的基于身份的可引用环签名方案，将环签名方案扩展为可引用的，任何人都可以从原始消息产生的环签名中推导出消息子串产生新的签名。该方案基于复合阶的双线性配对，证明了在子群决策困难问题假设下是匿名的，并在Diffie-Hellman困难问题假设下，针对ROM中自适应选择的消息攻击是不可伪造的。Au等［8］基于标准模型提出了一种安全且不受限制的基于身份的环签名方案。该方案在标准模型下证明了它的构造是安全的，并根据环签名中超级匿名性的定义方法，定义了一个新的基于身份的环签名的匿名级别，在此级别中，敌手可以指定用于创建用户密钥的随机性。赵艳琦等［9］采用对偶系统加密技术提出了一种基于身份的环签名方案。该方案结合了合数阶群上的双线性运算的正交性，从而将安全性规约为计算Diffie-Hellman困难问题。上述基于身份的环签名方案解决了PKI中证书管理问题，但是又存在新的密钥托管问题，因为PKG掌握着所有实体的密钥，有能力对所有实体间的通信进行监听或伪造。

为了解决上述两个问题，2003年Al-Riyami和Paterson［10］引入了无证书公钥密码学（CertificateLess Public Key Cryptography， CL-PKC）的概念。在CL-PKC中，用户的私钥由密钥生成中心（Key Generation Center， KGC）生成的部分私钥和用户自己选择的秘密值两部分组成。因此，即使恶意KGC泄露了KGC产生的部分私钥，攻击者也无法获得整个私钥来进行攻击。通过这种方式，CL-PKC不仅消除了ID-PKC系统中的密钥托管问题，也解决了PKI系统中的证书管理问题。Yuan等［11］提出了一个基于双线性映射的无证书阈值签名方案，但该方案在签名阶段需要（1）次双线性配对，因此，当相对较大时，签名阶段的计算开销相当高。张福泰等［12］对无证书加密、签名、密钥协商、签密等方面进行了总结，指出现有大多数方案都存在安全模型不合理、证明不严谨、有安全缺陷等问题。Karati等［13］在工业物联网环境下提出了一种基于双线性配对的无证书签名方案。在该方案中，签名者需执行两次指数运算，验证者执行一次双线性配对和两次指数运算，因此计算代价相对较大。然而，Zhang等［14］在方案［13］的基础上进行了改进，提出一种更轻量高效的基于椭圆曲线的无证书签名方案。并分析了四种类型的签名伪造攻击，证明了方案［13］无法实现所声称的安全特性。

综上所述，现有大多数环签名方案都存在以下问题：

1）证书管理和密钥托管问题。基于传统PKI和基于IDB-PKC的签名方案分别存在证书管理问题和密钥托管问题。

2）计算代价高。现有大多数环签名方案使用了高计算代价的双线性配对运算和模指数操作，计算代价高、效率低。

3）易遭受各种恶意攻击。没有考虑恶意KGC的攻击，KGC产生部分密钥，有能力对所有实体进行监听、伪造等，恶意用户也可以自行对实体的公钥进行替换攻击。

为了解决上述问题，本文提出了一种新的基于椭圆曲线的高效无证书环签名（Efficient CertificateLess Ring Signature， ECL-RS）方案，主要工作如下：

1）提出了一种新的基于椭圆曲线的高效无证书环签名方案，在不需要公钥证书的同时有效解决了密钥托管问题，具有自发性和匿名性，可保护用户身份和数据隐私性。

2）本文方案的安全性基于椭圆曲线离散对数问题和Diffie-Hellman问题，在随机预言机模型下证明了ECL-RS方案在公钥替换攻击和恶意KGC攻击下是不可伪造的，并具有正确性和匿名性等属性。

3）本文方案没有使用计算代价较高的双线性配对和指数操作，而是基于计算代价低、安全性高、灵活性好的椭圆曲线，与现有相关无证书环签名方案相比，ECL-RS方案具有较低的计算成本和更高的效率。

1 预备知识

本章主要介绍相关的数学基础理论。

1.1　椭圆曲线密码

ECC的密钥长度小，加密的文本和签名长度也小。此外，能更快地生成密钥，快速地签名和加解密，在硬件设备中能更快地获得椭圆曲线。

1.2　椭圆曲线离散对数问题

1.3　计算Diffie-Hellman问题

2 无证书环签名方案

本章主要对无证书环签名方案中的参数符号及其含义、无证书环签名方案的形式化定义及其安全模型进行介绍。

2.1　符号定义

本文所涉及到的相关符号说明如表1所示。

表1　符号说明

2.2　无证书环签名方案的形式化定义

2.3　无证书环签名方案的安全模型

若方案满足以下性质，则称环签名方案是安全的。

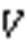
3）不可伪造性：考虑恶意用户（敌手Ⅰ）和恶意KGC（敌手Ⅱ）两种类型的攻击方法。

Ⅰ型敌手：敌手1无法访问系统主密钥，但敌手1可以用随机选择的整数来替换环中用户的公钥，因为没有公钥证书来保证用户公钥的真实性和有效性，此种攻击称为公钥替换攻击。

Ⅱ型敌手：敌手2能够访问系统主密钥，但敌手2不能获得任何用户的秘密值和私钥，也不能替换用户的公钥，此种攻击称为恶意KGC攻击。

游戏Ⅰ 在Ⅰ型敌手1和挑战者之间进行交互，详细步骤如下。

查询 敌手1执行多项式有限次查询，每次查询可能依赖于之前的查询结果。

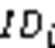
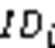
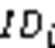
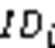
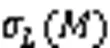
游戏Ⅱ 在敌手2和挑战者之间进行交互，详细步骤如下：

查询2进行多项式有界次查询，查询操作同游戏Ⅰ中所述，返回与游戏Ⅰ中一致的响应。但是，2可以使用系统主密钥自行计算任何用户的部分私钥。

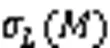
3 ECL⁃RS方案

图1　ECL-RS方案流程

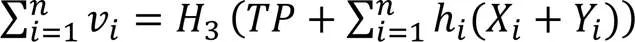
4 ECL‑RS方案安全性分析

定理1 ECL-RS方案具备正确性。

定理2 ECL-RS方案具备匿名性。

定理3 ECL-RS方案具备不可伪造性。

查询

查询

用户公钥替换：同游戏Ⅰ的用户公钥替换。

环签名查询：同游戏Ⅰ的环签名查询。

5 ECL‑RS方案性能分析

本章将ECL-RS方案与现有文献［7，18-21］中的部分无证书环签名方案进行比较。一般情况下，由于普通加减法和随机选择整数等操作运行时间少，可以忽略不计，因此仅针对以下几种操作的运行时间进行比较。使用MIRACL库在华为i5-1135G7处理器，主频2.40 GHz，16 GB内存和Windows 10操作系统的计算机上运行以下密码运算的运行时间如表2所示。

表2　密码符号表示及运算时间

表3　六种方案的计算代价对比（n=10） 单位： ms

6 结语

本文提出了一种新的基于椭圆曲线的高效无证书环签名方案ECL-RS。该方案采用了安全性高、密钥短、加密快、运算量小且灵活性好的椭圆曲线以降低计算开销，具有良好性能。ECL-RS方案的安全性依赖于ECDLP问题和CDH问题，在随机预言机模型下证明了本方案能够抵抗Ⅰ/Ⅱ型攻击，具有匿名性、不可伪造性等安全属性。性能分析表明，与现有相关环签名方案相比，ECL-RS方案在确保安全性的情况下效率更高，更加适用于轻量级物联网应用场景。

[1] RIVEST R L， SHAMIR A， TAUMAN Y. How to leak a secret［C］// Proceedings of the 2001 International Conference on the Theory and Application of Cryptology and Information Security， LNCS 2248. Berlin： Springer， 2001： 552-565.

[2] DIFFIE W， HELLMAN M. New directions in cryptography［J］. IEEE Transactions on Information Theory， 1976， 22（6）： 644-654.

[3] GUTMANN P. PKI： it’s not dead， just resting［J］. Computer， 2002， 35（8）： 41-49.

[4] SHIM K A. An efficient ring signature scheme from pairings［J］. Information Sciences， 2015， 300： 63-69.

[5] 张文芳，熊丹，王小敏，等. 基于RSA公钥密码体制的可选择可转换关联环签名［J］. 计算机学报， 2017， 40（5）：1168-1180.（ZHANG W F， XIONG D， WANG X M， et al. Selectively linkable and convertible ring signature based on RSA public key cryptosystem［J］. Chinese Journal of Computers， 2017， 40（5）： 1168-1180.）

[6] SHAMIR A. Identity-based cryptosystems and signature schemes［C］// Proceedings of the 1984 Workshop on the Theory and Application of Cryptographic Techniques， LNCS 196. Berlin： Springer， 1985： 47-53.

[7] WANG K， MU Y， SUSILO W. Identity-based quotable ring signature［J］. Information Sciences， 2015， 321： 71-89.

[8] AU M H， LIU J K， SUSILO W， et al. Realizing fully secure unrestricted ID-based ring signature in the standard model based on HIBE［J］. IEEE Transactions on Information Forensics and Security， 2013， 8（12）： 1909-1922.

[9] 赵艳琦，来齐齐，禹勇，等. 标准模型下基于身份的环签名方案［J］. 电子学报， 2018， 46（4）： 1019-1024.（ZHAO Y Q， LAI Q Q， YU Y， et al. ID-based ring signature in the standard model［J］. Acta Electronica Sinica， 2018， 46（4）： 1019-1024.）

[10] AL-RIYAMI S S， PATERSON K G. Certificateless public key cryptography［C］// Proceedings of the 2003 International Conference on the Theory and Application of Cryptology and Information Security， LNCS 2894. Berlin： Springer， 2003： 452-473.

[11] YUAN H， ZHANG F， HUANG X， et al. Certificateless threshold signature scheme from bilinear maps［J］. Information Sciences， 2010， 180（23）： 4714-4728.

[12] 张福泰，孙银霞，张磊，等. 无证书公钥密码体制研究［J］. 软件学报， 2011， 22（6）： 1316-1332.（ZHANG F T， SUN Y X， ZHANG L， et al. Research on certificateless public key cryptography［J］. Journal of Software， 2011， 22（6）： 1316-1332.）

[13] KARATI A， ISLAM S H， KARUPPIAH M. Provably secure and lightweight certificateless signature scheme for IIoT environments［J］. IEEE Transactions on Industrial Informatics， 2018， 14（8）： 3701-3711.

[14] ZHANG Y， DENG R H， ZHENG D， et al. Efficient and robust certificateless signature for data crowdsensing in cloud-assisted industrial IoT［J］. IEEE Transactions on Industrial Informatics， 2019， 15（9）： 5099-5108.

[15] KOBLITZ N. Elliptic curve cryptosystems［J］. Mathematics of Computation， 1987， 48（177）： 203-209.

[16] BONEH D， BOYEN X. Short signatures without random oracles［C］// Proceedings of the 2004 International Conference on the Theory and Applications of Cryptographic Techniques， LNCS 3027. Berlin： Springer， 2004： 56-73.

[17] POINTCHEVAL D， STERN J. Security proofs for signature schemes［C］// Proceedings of the 1996 International Conference on the Theory and Applications of Cryptographic Techniques， LNCS 1070. Berlin： Springer， 1996： 387-398.

[18] BOUAKKAZ S， SEMCHEDINE F. A certificateless ring signature scheme with batch verification for applications in VANET［J］. Journal of Information Security and Applications， 2020， 55： No.102669.

[19] YU H， WANG W. Certificateless network coding ring signature scheme［J］. Security and Communication Networks， 2021， 2021： No.8029644.

[20] ZHANG Y， ZENG J， LI W， et al. A certificateless ring signature scheme with high efficiency in the random oracle model［J］. Mathematical Problems in Engineering， 2017， 2017： No.7696858.

[21] WANG Z， FAN J. Flexible threshold ring signature in chronological order for privacy protection in edge computing［J］. IEEE Transactions on Cloud Computing， 2022， 15（9）： 1253-1261.

Efficient certificateless ring signature scheme based on elliptic curve

ZHU Xiuping1，2，3， LIU Yali1，2，3*， LIN Changlu2， LI Tao1，2，3， DONG Yongquan1

（1，，221116，；2（），350117，；3（），541004，）

Ring signature is widely used to solve the problems of user identity and data privacy disclosure because of its spontaneity and anonymity； and certificateless public key cryptosystem can not only solve the problem of key escrow， but also do not need the management of public key certificates； certificateless ring signature combines the advantages of both of the above mentioned， and has extensive research significance， but most of the existing certificateless ring signature schemes are based on the calculation of bilinear pairings and modular exponentiation， which are computationally expensive and inefficient. In order to improve the efficiency of signature and verification stages， a new Efficient CertificateLess Ring Signature （ECL-RS） scheme was proposed， which used elliptic curve with low computational cost， high security and good flexibility. The security statute of ECL-RS scheme stems from a discrete logarithm problem and a Diffie-Hellman problem， and the scheme is proved to be resistant to public key substitution attacks and malicious key generation center attacks under Random Oracle Model （ROM） with unforgeability and anonymity. Performance analysis shows that ECL-RS scheme only needs （+2） （is the number of ring members） elliptic curve scalar multiplication and scalar addition operations as well as （+3） one-way hash operations， which has lower computational cost and higher efficiency while ensuring security.

ring signature; elliptic curve; certificateless ring signature; efficiency; Random Oracle Model (ROM)

1001-9081（2023）11-3368-07

10.11772/j.issn.1001-9081.2022111801

2022⁃11⁃04；

2023⁃01⁃04；

国家自然科学基金资助项目（61702237）； 徐州市科技计划项目（KC22052）； 福建省网络安全与密码技术重点实验室（福建师范大学）开放课题（NSCL‑KF2021‑04）； 广西密码学与信息安全重点实验室（桂林电子科技大学）研究课题（GCIS202114）； 江苏师范大学研究生科研与实践创新计划项目（2021XKT1396）； 教育部产学合作协同育人项目（202101374001）。。

朱秀萍（1997—），女，四川内江人，硕士研究生，CCF会员，主要研究方向：公钥密码学、数字签名、物联网隐私保护； 刘亚丽（1981—），女，江苏徐州人，教授，博士，CCF高级会员，主要研究方向：信息安全、认证和隐私保护、区块链、车载自组织网络、密码算法和协议； 林昌露（1978—），男，福建大田人，教授，博士生导师，博士，CCF会员，主要研究方向：密码学、网络安全、秘密共享、安全多方计算、公钥密码学； 李涛（1998—），男，湖北黄冈人，硕士研究生，主要研究方向：无线射频识别认证、隐私保护、物联网安全、区块链； 董永权（1979—），男，江苏宿迁人，教授，博士，CCF会员，主要研究方向：Web信息管理、Web信息安全。

TP309

A

2023⁃01⁃10。

This work is partially supported by National Natural Science Foundation of China （61702237）， Science and Technology Planning Foundation of Xuzhou City （KC22052）， Opening Foundation of Fujian Provincial Key Laboratory of Network Security and Cryptology Research Fund， Fujian Normal University （NSCL-KF2021-04）， Opening Foundation of Guangxi Key Laboratory of Cryptography and Information Security， Guilin University of Electronic Technology （GCIS202114）， Postgraduate Research and Practice Innovation Program of Jiangsu Normal University （2021XKT1396）， Ministry of Education University-Industry Collaborative Education Program of China （202101374001）.

ZHU Xiuping， born in 1997， M. S. candidate. Her research interests include public-key cryptography， digital signature， Internet of Things privacy-preserving.

LIU Yali， born in 1981， Ph. D.， professor. Her research interests include information security， authentication and privacy-preserving， blockchain， vehicular ad-hoc network， cryptographic algorithms and protocols.

LIN Changlu， born in 1978， Ph. D.， professor. His research interests include cryptography， network security， secret sharing， secure multi-party computation， public-key cryptography.

LI Tao， born in 1998， M. S. candidate. His research interests include Radio Frequency Identification （RFID） authentication， privacy protection， Internet of Things security， blockchain.

DONG Yongquan， born in 1979， Ph. D.， professor. His research interests include Web information management， Web information security.