网格化分布式新安江模型并行计算算法

刘乾，张洋铭，2，万定生*

网格化分布式新安江模型并行计算算法

刘乾1，张洋铭1，2，万定生1*

（1.河海大学 计算机与信息学院，南京 211100； 2.南京银行股份有限公司，南京 210019）（ ∗ 通信作者电子邮箱dshwan@hhu.edu.cn）

近年来，网格化分布式新安江模型（GXM）在洪水预报中发挥了重大作用，但在进行洪水过程模拟时，模型数据量与计算量巨大，GXM的计算时间随着模型预热期的增加呈指数增长，严重影响GXM的计算效率。因此，提出一种基于网格流向划分与动态优先级有向无环图（DAG）调度的GXM并行算法。首先，对模型参数、模型构件、模型计算过程进行分析；其次，从空间并行性的角度提出了基于网格流向划分的GXM并行算法以提高模型的计算效率；最后，提出一种基于动态优先级的DAG任务调度算法，通过构建网格计算节点的DAG并动态更新计算节点的优先级以实现GXM计算过程中的任务调度，减少模型计算中数据倾斜现象的产生。在陕西省大理河流域与安徽省屯溪流域对提出的算法进行实验，在预热期为30 d、数据分辨率为1 km的情况下，相较于传统的串行算法，所提算法的最大加速比分别达到了4.03和4.11，有效提升了GXM的计算速度与资源利用率。

网格化分布式新安江模型；网格流向划分；并行计算；有向无环图；任务调度

0 引言

水文模型主要用于洪水预报，为防汛人员提供调度决策支持，在防洪减灾方面有着非常重要的意义。水文模型分为两类：集总式水文模型和分布式水文模型［1］。集总式水文模型的计算过程中没有考虑流域的空间差异性，采用一套统一、固定化的参数，在下垫面物理条件差异大、面积分布广的流域，该模型的洪水预报精度并不理想；分布式水文模型则充分考虑了流域内降雨空间分布不均以及下垫面物理参数差异对流域内产汇流的影响［2］，预报精度较高。典型的分布式水文模型有：分布式新安江模型（Distributed Xin’anjiang Model）、TOPMODEL模型（TOPography-based hydrological MODEL）［3］和TOPKAPI模型［4］等。

分布式新安江模型按照流域划分粒度又可分为：分块型分布式新安江模型与网格化分布式新安江模型（Grid-based distributed Xin’anjiang hydrological Model， GXM）。GXM是基于数字高程模型（Digital Elevation Model， DEM）实现的、以新安江模型为基础的分布式水文模型［5］。GXM将流域划分为大小一致的高精度网格单元后进行水文预报计算，计算过程主要包括对每个网格单元计算蒸散发、产流、分水源以及根据上下游依赖关系逐网格进行坡地汇流和河道汇流演算［6］。因此GXM计算过程的耦合性很高，多采用传统的串行计算方式，计算效率低，无法满足快速预报的需求。

针对上述问题，本文提出了一种基于网格流向划分与动态优先级有向无环图（Directed Acyclic Graph， DAG）调度的GXM并行算法，实现了GXM的并行计算与任务调度，提高了模型计算效率。本文的主要工作如下：

1）设计了GXM并行框架：首先从模型参数、模型构件、模型计算过程三个角度分析GXM；然后对流域进行网格流向划分，得到流域网格单元间的独立或者依赖关系，并在此基础上实现GXM的并行计算与任务调度。

2）提出了一种基于网格流向划分的多层级可并行网格划分算法，通过该算法得到可并行网格演算次序序列，从而实现GXM的并行计算，提高GXM的计算效率。

3）提出了一种基于动态优先级的有向无环图（DAG）调度算法，在计算过程中动态调整GXM资源分配，减少了GXM计算过程中数据倾斜现象的产生，提高了GXM计算资源利用率。

1 相关工作

分布式水文模型的并行化方式一般分为：空间上并行化、时间上并行化、时间和空间组合的并行化［7］。为了在计算过程中方便衡量模型并行化的性能，Liu等［8］提出了理论最大加速比（Theoretical Maximum Speedup Ratio， TMSR），即串行算法的计算时间与并行算法的计算时间的比值，并将TMSR作为分布式水文模型并行计算能力的评价指标。Liu等［9］针对分布式水文模型FSDHM（Fully Sequential Dependent Hydrological Models），基于OpenMP（Open Multi-Processing）实现了一种依据流向将模拟单元分层的并行算法，并在河北省清水河流域对该并行算法进行实验验证。在数据集分辨率为30 m，计算线程数为24的情况下，模型最大加速比达到12.49，并行算法有效提升了FSDHM的计算速度。秦泽宁等［10］针对WEP-L分布式水文模型汇流过程采用OpenMP设计了区域分解并行方法，有效提高了模型汇流过程的计算速度。目前对分布式水文模型并行化的研究大多数采用从空间上并行化的方式，通过将模型计算时相互独立的模拟单元并行处理，取得了良好的应用效果。笔者所在团队的前期工作中提出了基于流向的分布式水文模型并行计算方法［11］，实现了分布式水文模型的标准构建与并行化改造，本文在该研究的基础上从空间并行角度对GXM进行并行化研究，提出相应的GXM并行算法。

为了进一步提高分布式水文模型并行计算的效率，国内外研究人员对于模型并行计算过程中的任务调度和资源分配方式进行了大量研究。Liu等［12］针对分布式水文模型提出一种可扩展的分布式水文模型的两级并行化方法，该方法可以同时在子流域级和基本模拟单元级（例如网格单元）进行并行化。实验结果表明，两级并行化方法比仅在子流域级别并行化的方法具有更好的可扩展性，并且并行性能随着数据量和子流域数量的增加而提高。秦泽宁等［10］为了实现分布式水文模型并行计算中任务分配的负载均衡，设计了基于贪心算法的优化调度方法，有效提高了模型的并行效率。但是目前对GXM并行计算过程中的任务调度研究仍然不多。因此，本文提出一种基于动态优先级的DAG任务调度算法，以实现GXM并行计算过程中的任务调度，提升GXM并行计算的资源利用率。

2 GXM并行算法

2.1　GXM并行框架

从模型参数、模型构件、模型计算过程三个角度来对GXM进行分析，本文提出的GXM并行框架如图1所示。

图1　GXM并行框架

GXM参数主要包括集总式参数与以网格划分的模型参数。集总式参数一般为水文流域模型系数，每个流域对应一组参数；以网格划分的模型参数包含了流域下垫面条件、流域状态场与土壤含水量等信息，每个网格拥有独立的参数且不同网格之间参数独立。对上述参数采用NetCDF文件形式进行存储，NetCDF具有很强的灵活性，特别适用于大量多维度数据的传输与存储，具有读写效率高、灵活度高、压缩性高、使用与平台无关等特点［13］。

依据功能差异将GXM中的计算任务划分为四种类型的构件，分别为蒸散发构件、产流构件、分水源构件和汇流构件，以实现网格单元之间的关系解耦。每种构件内部又可以细化为不同的计算组件，构件划分如图2所示。

图2　GXM构件分类

针对各个构件在计算过程中的特点，将构件划分为两种类型：独立型构件和依赖型构件［14］。

1）独立型构件：计算过程中，独立型构件的网格计算单元之间的关系相互独立，无须考虑流域上下游计算单元间的依赖关系。独立性构件包括蒸散发构件、产流构件和分水源构件。

2）依赖型构件：计算过程中，依赖型构件需要考虑网格计算单元在时空间上的依赖性，根据计算单元上下游依赖关系计算。依赖型构件包括汇流构件。

2.2　构建网格流向矩阵

GXM依赖高分辨率的流域下垫面信息，通过提取流域内网格单元的流向信息，确定上下游网格单元间的流向关系，从而构建流域内的网格流向矩阵。

采用D8算法［15］确定网格单元水流方向，算法思路为：设定每个网格单元水流方向只有8种可能，即只流入与之相邻的8个网格中的一个网格，网格单元的8个流向用不同的数字表示，网格单元流向标记如图3所示。

图3　网格单元流向标记

在3×3的网格窗口中，首先计算中心网格与各相邻网格间的距离权落差，取距离权落差最大的网格作为中心网格的出流网格。网格间距离权落差计算公式如式（1）所示：

其中：表示需确定流向的网格单元高程，表示与之相邻的网格单元高程；指代距离权重，对角线网格取，其他正向网格取1；为网格单元边长。图4为网格流向矩阵及对应的水流流向矩阵示意图。

2.3　基于网格流向划分的GXM并行算法

2.3.1GXM过程分析

GXM以高精度网格作为模拟单元，有良好的预报精度。在GXM计算过程中，将每一个网格单元作为一个子流域处理，首先分别采用三层蒸散发模型、蓄满产流模型及自由水蓄水库结构对每个网格单元进行蒸散发计算、产流量计算、分水源计算，得到每一个网格单元的产流量与三水源；其次，按照流向顺序依次进行网格单元坡地汇流和河道汇流演算；最后，将流域内网格的地表径流、壤中流、地下径流演算至流域出口［16］。

2.3.2多层级可并行网格划分算法

GXM因为网格单元的计算耦合度较高，所以传统上多采用串行计算方法，按照流向顺序逐网格将流量演算至流域出口，导致GXM计算时间长、资源利用率低等问题。因此，本文提出一种多层级可并行网格划分算法，通过构建流域的网格流向矩阵、累积汇水面积矩阵和水系矩阵，分析挖掘出流域网格间的独立与依赖关系，找出流域内可并行网格的并行演算次序序列，实现多层级可并行网格的划分。

通过网格流向矩阵可以确定流域内所有网格单元的上游网格，按照网格流向矩阵中的流向，逐网格演算至流域出口。演算过程中所经过的网格的汇水量均增加一个单位，从而可得到流域的累计汇水面积矩阵。累计汇水面积矩阵存储了流域内每个网格单元的累计汇水量，矩阵中每一个数值代表了从上游汇流区流入当前网格的网格单元数量。当网格的集水面积超过某一阈值时，将该网格单元设定为河道网格，标记为1；低于此阈值的网格设定为非河道网格，标记为0。最后用这些标记好的网格单元构成河网水系矩阵。通过流向矩阵生成累计汇水面积矩阵以及水系矩阵的过程如图5所示。

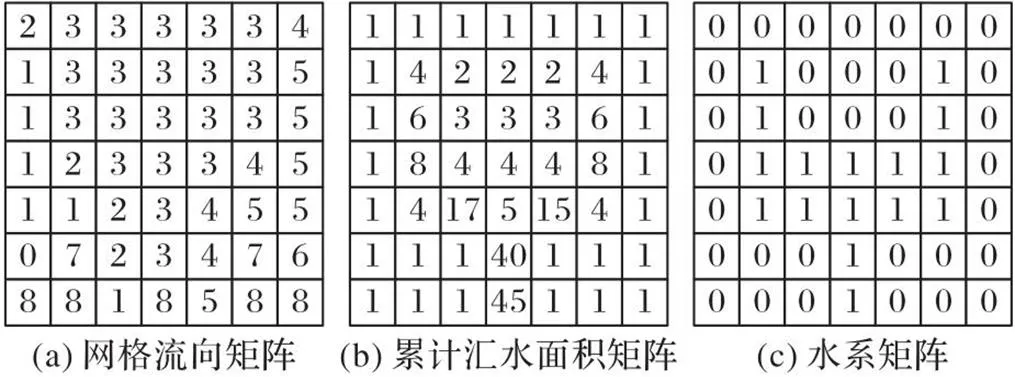
图5　累计汇水面积矩阵及水系矩阵生成过程

接着根据流域出流网格向上推演，对网格之间的演算关系进行解耦，通过多层级可并行网格划分算法计算出流域内网格的并行演算次序序列，从而实现GXM的并行计算。多层级可并行网格划分算法描述如下：

输入 网格流向，水系，累计汇水面积，累积汇水面积最大值，网格数，目标网格；

输出 返回每个网格的并行演算次序。

for←0 todo

所有网格赋初始值0；

for←0 todo

if

找出流域出口点，并赋值的演算次序为

（1）；

if1&&=

寻找流入该网格的上游网格；

返回的演算次序1；

；

break

for←0 todo

倒序排列；

while（∃=0） do

if0&&=1

返回演算次序=（1）；

break

else if0&&≠1

寻找该网格汇入的下游网格；

返回的演算次序1；

break

return 返回每个网格的并行演算次序

设流域内网格数量为，最大演算次序为，演算次序为，当前次序重复的网格数量为C，它们之间的关系如式（2）所示：

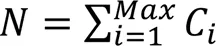
河道网格的演算次序按照河道汇流方向依次递增，并且非水系区域的网格单元在流域内的占比很大，这些网格单元的演算次序往往较小并且分布较为密集。因为具有相同演算次序的网格单元计算过程中不需要进行数据交换，完全相互独立，所以这些具有相同演算次序的网格单元可以并行计算，同时为不同层级演算次序的网格单元分配不同的计算线程，从而实现GXM的并行计算。各个网格单元间的数据通过内存进行传递交互，调度方式基于先到先服务方式。在山西省大理河流域与安徽省屯溪流域对上述提出的基于网格流向划分的GXM并行算法进行验证，发现并行算法的计算效率相较于传统的串行计算方法有着明显的提升。

3 基于动态优先级的DAG调度算法

3.1　数据倾斜

数据倾斜现象是指GXM在并行计算过程中，因为不同演算次序的任务量不同而造成的不同计算线程之间负载不平衡的问题。理想情况下，每个计算线程所分配的计算任务量接近，但在预热期长、流域面积广的情况下使用第2章提出的基于网格流向划分的GXM并行算法进行模型计算时，极易出现计算任务分配不均衡、资源浪费的问题。GXM在并行计算时产生的数据倾斜现象如图6所示。

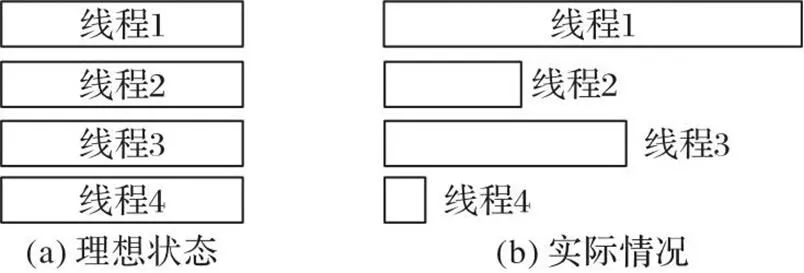
图6　数据倾斜现象

3.2　网格单元动态优先级划分算法

针对GXM计算中出现的数据倾斜现象，提出一种网格单元动态优先级划分算法。首先去除流域内无效网格，其次依据并行演算次序在网格计算节点之间添加有向边，从而形成由网格计算节点和有向边所构成的DAG，用于表达流域网格单元间的计算任务关系，如图7所示，图中的网格数值代表网格编号。DAG中的每个网格有若干个前置任务网格和一个后置任务网格。每个网格被认为是一个计算节点，每个计算节点有自身相关参数、前置任务集与后置任务集。

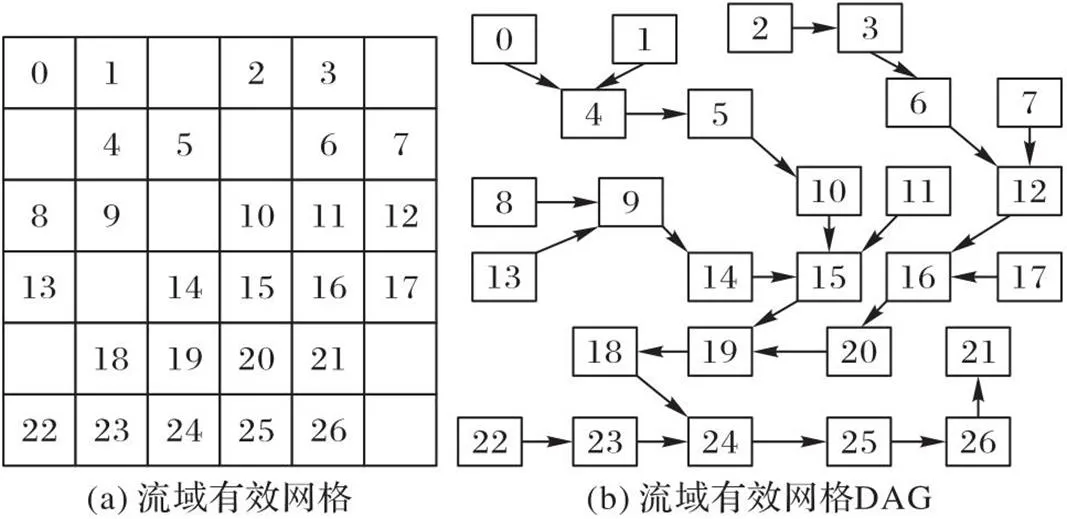
图7　流域有效网格单元的DAG

网格单元动态优先级划分算法首先会根据并行演算次序序列对计算节点的任务优先级进行初始化，并在模型计算过程中动态调整网格计算节点的任务优先级。通过定义式（3）、（4）计算节点的任务优先级：

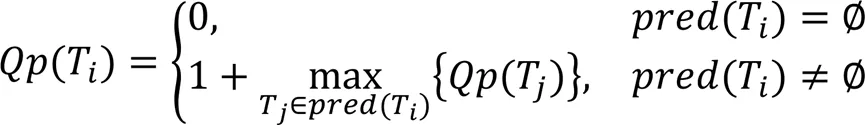
输入 节点个数，计算节点优先级，当前节点，每个网格初始演算次序， 线程数当前网格的下游网格坐标，某节点位置；

输出 剩余每个节点更新后的计算优先级。

for←0 todo

if为叶子节点

［］1；

else if为非叶子节点

［］=；

forall （in （1）） do

repeat

until

更新后置任务网格优先级［］1；

while（［］=［］） do

更新［］，节点在就绪队列等待；

返回更新后的；

break

更新［］，节点在就绪队列等待，节点更新为当前计算节点；

返回更新后的；

break

return 剩余每个节点更新后的计算优先级

3.3　基于关键路径的DAG调度算法

根据上面提出的网格单元动态优先级划分算法，提出基于关键路径的DAG任务调度算法来实现GXM并行计算中的任务调度。首先基于DAG计算任务的深度和动态优先级，建立任务状态队列包括就绪队列、运行队列和已完成队列。就绪队列包含了当前可执行的任务，即所有不存在前置任务的节点和前置任务已经执行完毕的节点；运行队列包含了正在运行的任务；任务执行完毕后，进入完成队列。其中，在任务进入就绪队列前，赋予任务节点三种属性类型：叶子节点、等待节点和关键节点。叶子节点为DAG中第一层节点，不包含前置任务，任务优先级初始化为1，在任务开始执行时就处于就绪状态；等待节点是将要执行的节点，当前任务完成时，它的后置任务进入就绪队列，成为等待节点；关键节点处于层数和深度之和最大的关键路径上，任务总体执行时间由关键节点决定，关键节点在所有等待节点中具有最高优先级［17］。

基于关键路径的DAG动态调度算法的基本思想为：将河道网格作为初始关键路径，当就绪节点进入运行队列执行完成后，从运行队列中自行剔除，并按照动态优先级划分算法更新执行结束的计算节点的后置任务优先级，从而在后续计算过程中不断更新关键路径并将计算节点按照任务优先级分配运行。GXM并行计算过程中的任务调度如图8所示。

图8　GXM并行计算过程中的任务调度

基于关键路径的DAG调度算法描述如下：

输入 计算节点个数，线程数，就绪队列中叶子节点个数，就绪队列中关键节点个数，就绪队列中等待节点个数，任务优先级，运行队列任务数，进入运行队列阈值；

输出 每个网格节点任务的计算结果。

根据流向网格构建计算任务DAG

for←0 todo

初始化任务优先级；

forall （in （1）） do

分配叶子节点进入就绪队列；

for←0 todo

while（<=） do

if［］=1 &&0

等待节点进入运行队列，计算流量，后置任务成为等待节点；

-1；

else if［］=1 &&≠0

关键节点进入运行队列，计算流量，更新后置任务；

-1；

执行计算任务，结果进入已完成队列；

if=0

返回计算结果；

break

return 每个网格节点任务的计算结果

4 实验与结果分析

4.1　实验数据准备

实验硬件环境是一台内存大小16 GB，CPU型号为Intel E5-2630，操作系统为Windows Server 2008的个人计算机。实验选取陕西省榆林市大理河2020年6月1日后30 d、60 d、90 d的流域水文数据与安徽省屯溪2020年6月1日后30 d的流域水文数据作为模型输入，对本文提出的基于网格流向划分的GXM并行算法与基于动态优先级的DAG调度算法进行实验验证。

4.2　实验结果分析

首先采用流域网格分辨率为1 km的大理河数据，设置预热期为30 d内的不同天数，对比串行算法和基于网格流向划分的GXM并行算法在大理河流域内的模型计算时间，结果如图9（a）所示，可以看出在使用并行算法后：在预热期为3 d时，GXM加速比为1.25；当预热期增加到30 d，GXM并行加速比达到4.03；并且模型预热期达到21 d以后，串行算法的计算时间明显增加，而GXM并行算法的计算时间一直没有超过80 s，与原有的串行算法相比，基于网格流向划分的GXM并行算法的计算效率得到了明显提升。

采用基于共享内存模型的OpenMP实现GXM并行算法，在大理河流域进行对比实验，结果发现GXM并行加速比在预热期为30天的情况下达到了5.01，模型计算时间进一步减少，模型计算效率得到了提高。

随后采用流域网格分辨率为1 km的屯溪数据，设置预热期为30 d内的不同天数，对比串行算法和基于网格流向划分的GXM并行算法在屯溪流域内的模型计算时间，结果如图9（b）所示。在预热期为3 d时，GXM加速比为1.1；当预热期增加到30 d，GXM并行加速比达到4.11。可以看出，基于网格流向划分的GXM并行算法的计算效率比原有的串行算法得到了明显提高。

Freitas等［18］针对MGB（Modelo de Grandes Bacias）水文模型提出了一种基于矢量化与线程并行的CPU并行算法。该算法利用AVX-512矢量指令集与基于共享内存模型的OpenMP对MGB中的STE（timestep）、DIS（discharge）、CON（continuity）三个主要程序模块进行并行化处理。在尼日尔河流域对该算法进行实验验证，实验发现基于矢量化与线程并行的CPU并行算法：在CPU型号为Intel Core i7-7820X的硬件环境下，设置计算线程数为8，MGB模型的最大加速比达到了5.27；在CPU型号为Intel Core i9-7900X的硬件环境下，设置计算线程数为10，MGB模型的最大加速比达到了5.99。与本文提出的基于网格流向划分的GXM并行算法相比，基于矢量化与线程并行的CPU并行算法同样拥有较好的并行性能，这是因为该算法不仅利用OpenMP实现了线程并行化，还利用矢量指令集实现了数据并行化。但是基于矢量化与线程并行的CPU并行算法仍然存在以下局限性：首先，该并行算法对计算机的硬件环境要求较高，因为该并行算法需要在支持AVX512矢量指令集的硬件环境下运行，然而目前很多计算机的CPU并不支持AVX512矢量指令集；其次，该并行算法是通过对模型内部中的矢量操作进行矢量化改造来实现模型的并行化，这就要求模型内部中无法进行矢量化改造的线性操作不能过多，否则无法达到算法预期的并行效果；并且该并行算法没有指出如何减少并行计算过程中线程间的通信开销。而本文提出的基于网格流向划分的并行算法是从模型自身结构出发，利用流域下垫面的DEM数据对流域网格进行区域分解，获得了流域网格的演算次序，从而实现了模型的并行计算，因此本文提出的并行算法对计算机的硬件环境没有严格要求；而且本文提出的基于动态优先级的DAG调度算法还实现了计算任务优先级的动态划分，从而实现了并行计算过程中的任务调度，能有效降低线程间的通信开销。

接着采用流域网格分辨率为0.5 km的大理河流域数据，相较于分辨率为1 km网格数据，模型的计算任务节点增加了1倍以上，模拟单元多达11 448个。设置预热期为30 d、60 d、90 d情况下，采用基于动态优先级的DAG调度算法对GXM并行计算进行任务调度，验证调度算法对于GXM并行效率的影响，实验结果如表1所示。

表1　调度算法对并行计算的影响

从表1可以看出，当预热期达到30 d时，GXM并行计算时间缩短了11.31%；当预热期达到60 d时，GXM并行计算时间缩短了30.08%；当预热期增加到90 d时，GXM并行计算时间相较于未采用调度算法的计算时间缩短了35.63%。因此，采用基于动态优先级的DAG调度算法对GXM并行计算进行任务调度能够有效提升GXM并行计算的效率。

针对90 d的预热期，设置不同的计算线程数，监测GXM并行计算的并行效率［19］，即加速比与参与计算的线程数比值，结果如表2所示。

由表2可以看出：采用了调度算法后的并行效率明显高于未采用调度算法的并行效率，在线程数为4时，采用调度算法后的并行效率达到了0.90。随着计算线程数的增加，GXM的并行效率在逐渐降低，这是因为当计算线程数增加时，用于任务调度的计算资源开销在逐渐增大，制约了并行计算性能的提升；但采用调度算法后的并行效率一直优于未采用调度算法的并行效率。这表明通过基于动态优先级的DAG调度算法能够有效缓解当计算线程数增加时出现的线程间负载不均衡的问题，减少计算线程的闲置等待时间，从而能较好地提升计算机的资源利用率。

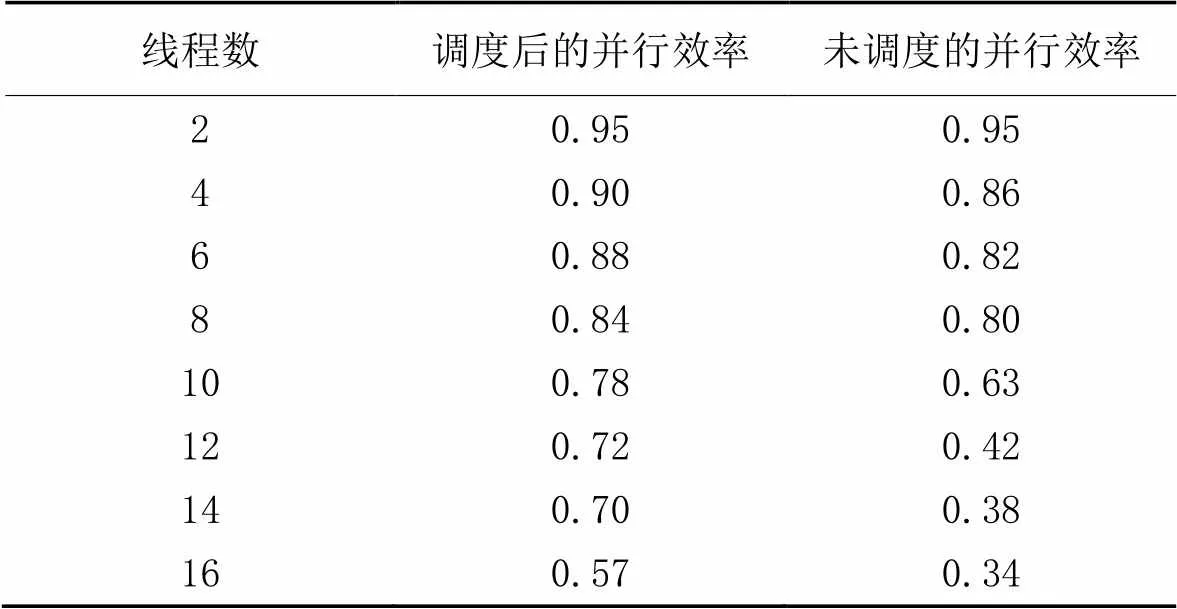
表2　并行效率对比

5 结语

针对GXM的串行计算效率低的问题，本文提出了基于网格流向划分的GXM并行算法。首先构建网格流向矩阵，利用多层级可并行网格划分算法得出流域网格的并行演算次序序列，实现GXM的并行计算，提升了GXM的计算速度；其次，针对并行计算中的任务调度问题，提出基于动态优先级的DAG调度算法，通过并行演算次序序列构建流域计算节点DAG并使用动态优先级划分算法动态更新网格计算节点优先级，实现GXM并行计算中的任务调度，有效提升了GXM并行计算的资源利用率。未来会考虑如何在并行计算中减少网格计算单元间的大量数据交互并利用矢量指令实现GXM的数据并行化，进一步提升GXM的并行计算效率。

[1] 芮孝芳. 对流域水文模型的再认识［J］. 水利水电科技进展， 2018， 38（2）： 1-7.（RUI X F. More discussion of watershed hydrological model［J］. Advances in Science and Technology of Water Resources， 2018， 38（2）： 1-7.）

[2] 芮孝芳. 论流域水文模型［J］. 水利水电科技进展， 2017， 37（4）：1-7， 58.（RUI X F. Discussion of watershed hydrological model［J］. Advances in Science and Technology of Water Resources， 2017， 37（4）：1-7， 58.）

[3] BEVEN K J， KIRKBY M J， FREER J E， et al. A history of TOPMODEL［J］. Hydrology and Earth System Sciences， 2021， 25（2）： 527-549.

[4] LIU Z， MARTINA M L V， TODINI E. Flood forecasting using a fully distributed model： application of the TOPKAPI model to the Upper Xixian Catchment［J］. Hydrology and Earth System Sciences， 2005， 9（4）： 347-364.

[5] 姚成. 基于栅格的分布式新安江模型构建与分析［D］. 南京：河海大学， 2007： 16-20.（YAO C. Development and application of grid-based distributed Xin’anjinag model［D］. Nanjing： Hohai University， 2007： 16-20.）

[6] 姚成，李致家，张珂，等. 基于栅格型新安江模型的中小河流精细化洪水预报［J］. 河海大学学报（自然科学版）， 2021， 49（1）：19-25.（YAO C， LI Z J， ZHANG K， et al. Fine-scale flood forecasting for small and medium-sized rivers based on Grid-Xin’anjiang model［J］. Journal of Hohai University （Natural Sciences）， 2021， 49（1）：19-25.）

[7] 叶翔宇，李强，郭禹含，等. 高性能并行分布式水文模型研究进展［J］. 地理科学进展， 2022， 41（4）：731-740.（YE X Y， LI Q， GUO Y H， et al. Progress of research on high-performance parallel distributed hydrological model［J］. Progress in Geography， 2022， 41（4）： 731-740.）

[8] LIU J， ZHU A X， QIN C Z. Estimation of theoretical maximum speedup ratio for parallel computing of grid-based distributed hydrological models［J］. Computers and Geosciences， 2013， 60： 58-62.

[9] LIU J， ZHU A X， LIU Y， et al. A layered approach to parallel computing for spatially distributed hydrological modeling［J］. Environmental Modelling and Software， 2014， 51： 221-227.

[10] 秦泽宁，黎曙，周祖昊，等. 分布式水文模型区域分解并行计算方法及其应用［J］. 水电能源科学， 2020， 38（10）：1-4， 12.（QIN Z N， LI S， ZHOU Z H， et al. Domain decomposition parallel computing method of distributed hydrological model and its application［J］. Water Resources and Power， 2020， 38（10）：1-4， 12.）

[11] 河海大学. 基于流向的分布式水文模型并行计算方法： 202210254598.1［P］. 2022-05-10.（Hohai University. Parallel computing method for distributed hydrological models based on flow direction： 202210254598.1［P］. 2022-05-10.）

[12] LIU J， ZHU A X， QIN C Z， et al. A two-level parallelization method for distributed hydrological models［J］. Environmental Modelling and Software， 2016， 80： 175-184.

[13] 王想红，刘纪平，徐胜华，等. 基于NetCDF数据模型的海洋环境数据三维可视化研究［J］. 测绘科学， 2013， 38（2）： 59-61.（WANG X H， LIU J P， XU S H， et al. Visualization of marine environment data based on NetCDF data model［J］. Science of Surveying and Mapping， 2013， 38（2）： 59-61.）

[14] 刘军志，朱阿兴，秦承志，等. 分布式水文模型的并行计算研究进展［J］. 地理科学进展， 2013， 32（4）： 538-547. （LIU J Z， ZHU A X， QIN C Z， et al. Review on parallel computing of distributed hydrological models［J］. Progress in Geography， 2013， 32（4）： 538-547.）

[15] 邬伦，汪大明，张毅.基于DEM的水流方向算法研究［J］. 中国图象图形学报， 2006， 11（7）： 998-1003. （WU L， WANG D M， ZHANG Y. Research on the algorithms of the flow direction determination in ditches extraction based on grid DEM［J］. Journal of Image and Graphics， 2006， 11（7）： 998-1003.）

[16] 李致家，姚成，汪中华. 基于栅格的新安江模型的构建和应用［J］. 河海大学学报（自然科学版）， 2007， 35（2）： 131-134.（LI Z J， YAO C， WANG Z H. Development and application of grid-based Xin’anjiang model［J］. Journal of Hohai University （Natural Sciences）， 2007， 35（2）： 131-134.）

[17] 王命全，于炯，田园，等.网格环境中基于负载均衡的工作流调度算法［J］.计算机应用，2010，30（12）：3184-3186.（WANG M Q， YU J， TIAN Y， et al. Workflow scheduling algorithm based on load balance in grid［J］. Journal of Computer Applications， 2010， 30（12）：3184-3186.）

[18] FREITAS H R A， MENDES C L， ILIC A. Performance optimization and scalability analysis of the MGB hydrological model［C］// Proceedings of the IEEE 27th International Conference on High Performance Computing， Data， and Analytics. Piscataway： IEEE， 2020： 31-40

[19] ZHANG A， LI T， SI Y， et al. Double-layer parallelization for hydrological model calibration on HPC systems［J］. Journal of Hydrology， 2016， 535： 737-747.

Parallel computing algorithm of grid-based distributed Xin’anjiang hydrological model

LIU Qian1， ZHANG Yangming1，2， WAN Dingsheng1*

（1，，211100，；2，210019，）

In recent years， the Grid-based distributed Xin’anjiang hydrological Model （GXM） has played an important role in flood forecasting， but when simulating the flooding process， due to the vast amount of data and calculation of the model， the computing time of GXM increases exponentially with the increase of the model warm-up period， which seriously affects the computational efficiency of GXM. Therefore， a parallel computing algorithm of GXM based on grid flow direction division and dynamic priority Directed Acyclic Graph （DAG） scheduling was proposed. Firstly， the model parameters， model components， and model calculation process were analyzed. Secondly， a parallel algorithm of GXM based on grid flow direction division was proposed from the perspective of spatial parallelism to improve the computational efficiency of the model. Finally， a DAG task scheduling algorithm based on dynamic priority was proposed to reduce the occurrence of data skew in model calculation by constructing the DAG of grid computing nodes and dynamically updating the priorities of computing nodes to achieve task scheduling during GXM computation. Experimental results on Dali River basin of Shaanxi Province and Tunxi basin of Anhui Province show that compared with the traditional serial computing method， the maximum speedup ratio of the proposed algorithm reaches 4.03 and 4.11， respectively， the computing speed and resource utilization of GXM were effectively improved when the warm-up period is 30 days and the data resolution is 1 km.

Grid-based distributed Xin’anjiang hydrological Model (GXM); grid flow direction division; parallel computing; Directed Acyclic Graph (DAG); task scheduling

1001-9081（2023）11-3327-07

10.11772/j.issn.1001-9081.2022111760

2022⁃11⁃24；

2023⁃02⁃15；

国家重点研发计划项目（2018YFC1508106）。

刘乾（1998—），男，江苏南京人，硕士研究生，CCF会员，主要研究方向：分布式水文模型并行计算； 张洋铭（1997—），男，江苏徐州人，硕士研究生，CCF会员，主要研究方向：分布式水文模型并行计算； 万定生（1963—），男，江苏溧阳人，教授，CCF会员，主要研究方向：数据管理、数据挖掘。

P333

A

2023⁃02⁃17。

This work is partially supported by National Key Research and Development Program of China （2018YFC1508106）.

LIU Qian， born in 1998， M. S. candidate. His research interests include parallel computing of distributed hydrological models.

ZHANG Yangming， born in 1997， M. S. candidate. His research interests include parallel computing of distributed hydrological models.

WAN Dingsheng， born in 1963， professor. His research interests include data management， data mining.