精准把握学习节点，促进学生知识建构

［摘  要］ 学习节点是基于学习目标，在学生探究知识过程中必须经历的关键节点（环节）。教师要关注学生学习的节点，在关键的位置精心设计环节，认真实施教学流程，使学生在数学学习中经历知识生成，体验知识建构过程中的快乐，不断提升数学核心素养。

［关键词］ 学习节点；知识建构；数学思考；思维品质；学科素养

作者简介：陈丽华（1982—），本科学历，中小学一级教师，常熟市学科带头人，从事小学数学教学研究工作，曾获苏州市中小学教师专业素养大赛一等奖，“一师一优课”部级优课。

节点，通常来说，是指局部的膨胀（像一个个绳结一样），抑或是一个交会点。其实质，就是关键环节。学习节点是基于学习目标，在学生探究知识过程中必须经历的关键节点（环节）。在数学教学时，教师准确定位每个学习节点，利于激发学生的数学思考，不断深入探究知识，引领学生的数学思维向纵深发展，在经历知识形成的过程中，发展学生的深度学习，从而使学生获得更好的学习能力。笔者结合自己的教学实践，从关键的学习节点出发，探究学生深度学习、促进知识建构的策略。

一、定位已有经验，把握知识生长节点

学生学习数学是基于已有认知经验进行知识建构的过程。在教学中，教师要善于从学生的已有经验出发，引导学生进行新知探究。在生长新知识时，要突出已有经验的支撑作用，就需要教师深入了解学生真实的学情，具体来说包含学习个体的生长环境、生活经验、已具有的学习经验。通过前测练习，深入了解学生的学习起点。在此基础上，结合学习内容的编排特点和学生的认知规律，合理设计教学环节，精心组织每个教学流程，引导学生进行高效的数学学习，让学生的已有经验助推新知的生长，有效进行数学知识的建构，形成良好的认知结构。

例如，教学“认识几之分之一”时，教师基于学生的已有认知经验，从具体生活实例中展开对话，帮助学生建构分数的初步认知。

1. 分物：认识分数产生的基础

师：明明和红红去公园野餐，他们两人怎样分配食品才公平？

生1：把4个苹果平均分成2份，每人分得1份是2个。

师：怎样用式子表示苹果的分法？

生1：4÷2=2（个）。

生2：把2瓶矿泉水平均分成2份，每人分得1份是1瓶水，2÷2=1（瓶）。

师：刚刚分的苹果和矿泉水的总数都是2的倍数，可以直接平均分给2人。现在分1个蛋糕，该怎样分呢？

生3：把1个蛋糕平均分成2份，每人分得1份，是蛋糕的一半或半个蛋糕。

师：怎样列式表示呢？

生3：1÷2是半个。

师：半个蛋糕可以用怎样的数来表示呢？

生3：半个蛋糕可以用来表示。

师：真棒！你知道。你来写一写这个数。是啊，个就是半个。这个数与我们之前学过的数长得不太一样。你能说一说它的样子吗？

生3：中间有一条线，线上一个数，线下一个数。

师：是的，这个数与之前我们认识的数不一样。像这样的数，就是我们要认识的新数——分数。板书：认识分数。

师：分数是怎样产生的呢？我们来看一段视频。

教师播放《分数的产生》视频，使学生了解分数的演变过程。

师：原来分数是在分物品的过程中逐步产生的，经过了漫长的演变，才变成了我们今天见到的这个样子。谁来说一说，我们刚才是怎样得到这个分数的。

生4：把1个蛋糕平均分成2份，每份是蛋糕的一半，就是蛋糕的。

师：怎样写呢？

师生共写，读出二分之一。

2. 分图：理解分数形成的过程

师：怎样用1张长方形的纸表示出它的呢？

学生自己尝试动手操作，教师分组展示。

师：刚刚三位同学展示了自己的。这些分法有什么共同的地方？

生5：虽然分的形状不同，但都是把这个长方形平均分成2份，涂色都是它的。

师：空白部分是多少呢？

生5：空白部分也是长方形的。

师：表示长方形的，与每份的形状有关系吗？与什么有关系。

生5：与每份的形状无关，关键是要把这个长方形平均分成2份。

……

教师准确定位学生的已有“平均分”的知识生长节点，从分“野餐的食物”出发，经历分“4个苹果、2瓶矿泉水”开始，结合用除法算式表示，呈现平均分的过程和结果，扩充数域范圍到“把一个蛋糕平均分成2份，怎样表示一半”，沟通了分数与除法之间的内在联系，让学生体会不能用整数表示平均分的结果时，可以用新的数（分数）来表示。结合分物，从外在形式和内在含义的角度认识的含义，进一步拓展分数的数域。

二、通过实践操作，开启内化节点

动作是思维的起始，学生的思维离不开动作的伴随。实践表明：学生通过自己的实践活动发现的知识，理解得比较深刻，掌握得也比较牢固。因此，在小学数学教学中，教师要结合学生的认知规律，精心选择动手操作的学习材料，为学生的探究发现创设活动空间，给予学生实践操作的机会，使学生在操作中体验，进一步感悟和思考数学知识，把握知识的内化节点，不断开启已有经验向新知的升级改造之路，深度建构新知。

例如，教学“射线、直线和角”时，教师利用实践操作，让学生经历图形的抽象过程，引导学生理解“无限长”，进一步内化射线、直线、线段的特征，建立角的概念。

1. 点动成线，初步建构新知

教师先出示一个点。

师：这是一个什么图形？

生（齐）：点。

师：点是最基本的图形。想一想，通过点在一个平面上运动，轨迹会是什么样的图形？

生（齐）：直线、线段……

教师由课件演示点动成线的过程。

师：刚刚，一个点沿着固定的方向，做不同方式的运动，可以形成不同的线。谁能说一说已经认识了哪些线，它有什么特点？

生1：第一个图形是线段，它直直的，有两个端点。

生2：第二个图形是直线，直直的，没有端点。

师：没有端点，就是说明它可以怎么样？

生2：直线可以向两边无限延伸，说明长度是无限的。

师：第三个图形呢？有什么特点？

生3：也是直直的，只有一个端点，可以向没有端点的另一端延伸。

2. 实践操作，感悟图形特征

（1）想象射线射出的轨迹

师：想一想，把点继续向一端延伸，不停歇，会出现什么情况？

学生想象后，教师动画演示：一个光源（点）射出一条线，直至射出地球，射向浩瀚的宇宙。

师：像这样一直延伸下去，有没有尽头？

学生惊叹：一直延伸，没有尽头，从一点射出无限长。

师：像这样的线，就是射线。说一说，与刚才的直线、线段相比，射线有什么特点？

生（齐）：直直的，只有一个端点，无限长。

（2）动手画射线

师：如果要你在纸上画一条射线，你怎样画出射线的特点呢？

学生动手画射线后，教师找出有特点的展示，并让学生说一说自己的想法。

生4：射线从一点出发。为了表示它无限延伸，我一直画到纸的最边上，外面还有，长度是无限的。

生5：射线从一点出发，后面画细一点，表示还在延伸中。

生6：射线从一点出发，后面用小点表示，说明点还在向后延伸。

在纠正错误的画法后，教师示范画射线。

师：画射线，只需要在一端画出端点，表示射线的起点。

（3）说一说生活中哪些线可以看作射线

师：你在生活中，见过哪些线可以看作射线？

学生举例：城市楼顶上的射灯射出的光线、手电筒的光线……

在上述的教学环节中，教师从点与线的联系出发，紧扣“点动成线”，让点沿着固定的方向运动，描出轨迹，使学生复习“线段、直线的特征”，按顺序引入射线，顺应学生的认知，体现知识的逻辑结构，并使学生在动态的想象中认识射线，内化“无限长”，特别是突出射线的无限长时，教师采用课件演示射出地球、射向浩瀚的宇宙的场景，给学生留下了无法磨灭的印记。结合学生的实践操作，教师让学生进一步感悟射线的特征，内化认知，实现了旧知“线段、直线”和新知“射线”的无缝衔接。

三、进行应用拓展，掌握深入节点

学生通过探究活动发现新知、建构新知后，需要及时通过应用练习来巩固新知、深化理解，这样掌握的知识就不易遗忘。教师可以引导学生从实际问题中发现数学问题，应用数学知识解决问题，巩固认知。教师还可以引导学生通过应用拓展，掌握知识的深入节点，不断实现学生的数学智慧的生长。

例如，教学“长方形的周长”时，教师安排了这样一道练习，让学生进一步拓展周长的应用。

王叔叔要用篱笆围一个长5米，宽4米的鸡圈，鸡圈一面靠墙，需要篱笆多少米？

学生独立画图计算后，教师分组出示，进行集体交流。

生1：把长靠墙（图1），这样需要的篱笆的长度就是一条长加上两条宽的长度。即5+4×2=13（米）。

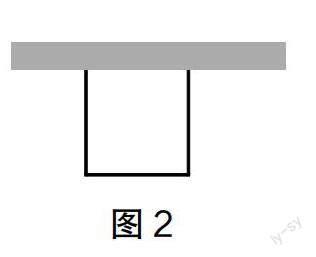
生2：把宽靠墙（图2），这样需要的篱笆的长度就是两条长加上一条宽的长度。即4+5×2=14（米）。

生3：也可以依据长或宽靠墙的情况，先求出长方形的周长，再减去一条长或宽，就可以求出实际需要篱笆的长度。即（5+4）×2=18（米），长靠墙：18-5=13（米），宽靠墙：18-4=14（米）。

学习长方形的周长后，教师安排这样的练习，既让学生经历用数学知识解决实际问题的过程，又在分类拓展中发展学生的思维，使学生深入理解知识，掌握知识的深入节点，不断激活学生的认知，修正对知识的不足认知，进行系统的知识建构，引导学生从不同角度分析问题，感受不同思考对于解决问题的价值，进一步培养学生灵活运用知识解决问题的能力，提升学生对数学学习的兴趣。

四、有效回顾总结，感悟反思节点

学生数学学习的过程，是主动建构知识的过程。在这个过程中，往往伴生着不间断的对数学知识的质疑、生成与反思的过程。只有经过回顾与反思，学生才能对知识有深刻的理解，真正达到融会贯通的程度。教师在数学教学活动中，要有意识地创设让学生回顾与反思的时机，给予学生充足的反思时间，不走过场，不流于形式，引导学生踏踏实实地做好知识的反思活动，认真梳理新知的探究过程，整理在学习过程中获得数学思想和方法，总结学习经验。在反思的节点，教师要深化学生的认知经验，使学生对知识的理解从零碎化、片面化走向系統化和整体化，进一步使学生的学习能力和思考能力得到长足的发展。

例如，教学“圆的面积计算”时，教师引导学生进行回顾总结所学习的内容，引导学生感悟数学思想方法，进一步发展学生的数学反思能力。

师：回顾我们刚刚经历的圆的面积计算公式的推导过程，你有什么收获？

生1：利用割补法，把圆这个不熟悉的图形转化成熟悉的图形（长方形、三角形、梯形），真是一个很好的方法。

生2：不管把圆转化成什么图形，改变的只是图形的形式，面积大小始终不变。

生3：推导圆的面积时，要找准转化后的图形与圆之间的等量关系。

师：图形面积转化的关键是什么？

生4：关键就是把复杂的新知转化为简单的旧知，由陌生到熟悉。

生5：转化的策略是解决面积公式推导问题的利器。

生6：在推导面积公式进行转化前，大胆的想象也是不可缺少的。

……

通过回顾与总结，进一步感悟所得。在知识的反思节点中，教师及时让学生寻找知识点的共性，沟通内部关联，帮助学生更好地建立知识网络，实现整体建构。

总之，数学教学中，教师要关注学生学习的节点，在关键的位置精心设计环节，认真实施教学流程，使学生在数学学习中经历知识生成，体验知识建构过程中的快乐，不断提升数学核心素养。