在探究中深化 在经历中发展

［摘  要］ 为了引导学生自主发现“最优”方案，教师以学生熟悉的情境为切入点，凸显了数学学习的现实意义，有效地激发了学生的数学学习热情。在解决问题的过程中，教师坚持“以生为主”，关注学生发展，鼓励学生通过思考、分析、比较等数学活动逐渐优化思想，从而提炼出数学模型，以此提升学生解决实际问题的能力。

［关键词］ 最优方案；学生发展；数学模型

作者简介：吕庆华（1976-），本科学历，中小学一级教师，从事小学数学教学与研究工作。

在“打电话”教学中，为了让学生体会“最优”的价值，教师以解决实际问题为起点，通过有效的启发和指导，鼓励学生积极参与、积极探索，以此发展学生的数学思维，提升学生的数学建模能力。

一、教学实录

1. 创设情境，引出问题

数学知识是抽象的、枯燥的，若在教学中只关注知识的讲授，而不重视学生学习兴趣的激发，这样的数学课堂一定是乏味的、低效的。因此，在教学中，为了激发学生的数学学习兴趣，让学生更好地体验生活中的数学味，教师在引出问题时常常会借助情境来淡化数学的抽象感和枯燥感，从而让数学课堂焕发无限活力。

某日深夜，119指挥中心接到报警，某小区发生煤气爆炸，需要紧急救援。因火势蔓延较快，需要召集正在休息的15名队员一同参与救援。（教师演示动画）

师：如果你是队长，你想用什么样的方式通知其他队员呢？

生1：微信或者QQ。

生2：电话。

生3：发短信。

生4：邮件。

……

師：非常好，大家知道得真多。火灾发生在深夜，你认为哪种方式既快捷又方便，同时确保通知到每名队员呢？

生齐声答：打电话。

师：你们和队长的想法不谋而合，他也选择了同样的方式。

师：想一想，如何打电话才更高效呢？

在引入阶段，教师以“救援”为切入点，让学生切身体会“高效”在生活中的价值，从而为后面的探究“最优”方案做好了铺垫。同时，通过演示火灾场景，让学生切实感知火灾的危害，从而培养安全用火、安全用电的好习惯。

2. 分析比较，探究“最优”

在探究“最优”的过程中学生大多需要经历比较、分析、交流、争论等过程，从而使解决问题的方案向“最优”转化，以此提升解决问题的效率。

师：如果每打一个电话需要1分钟，确保通知到每名队员需要多少分钟呢？

生5：如果逐一打，15个人需要15分钟。

师：这个时间太长了，大家刚刚也看到了，火势蔓延得很快，第一批救援人员只能控制火势，很难迅速将火扑灭。现在大家必须帮队长想一个更快的解决方案。（学生积极交流）

生6：可以大家一起打。

师：具体说说你的想法。

生6：可以将15人分成几个小组，这样队长只要通知组长，组长再通知队员就可以了。

师：很好的想法，如果将15人分为3组，这样确保通知到每名队员需要几分钟呢？（师生共同交流）

生7：这样队长打电话需要3分钟，组长打电话需要4分钟，所以一共需要7分钟。

师：很好，采用分组的方法打只需要7分钟，极大地提高了通知效率。谁来说一说，为什么这样打会更省时呢？

生8：如果逐一打就只能1个人打，分组后是4个人一起打，打的人多了自然也就快了。

师：说得很好，抓住了问题的本质。确实，打的人越多也就越省时。

师：这样分组后确实省时了，不过7分钟对于救援来讲还是动作太慢了，所以还需要对刚刚的打电话的形式进一步优化，你还有其他方案吗？

生9：可以让更多的人参与打电话。

师：具体怎么打呢？

生9：让所有的人都参与进来，接到通知就立刻把消息传递出去。

师：大家想一想，这样较前面的分组方案来比，哪个方案更快呢？

学生齐声答：后面的方案更快。

师：谁来分析一下，为什么后面的会更快呢？

生10：只要知情人都打电话，这样参与的人会越来越多，自然信息传播得也越快。

师：确实是个不错的想法，大家立了大功了。

这样，通过对比分析发现，若只是1个人打电话将会浪费很多的救援时间，为此学生提出了新方法，即“知情人都打电话”，从而通过交流、分析使问题解决逐渐向“最优”方案转化。

3. 优化思想，建构模型

在小学阶段，学生的建模意识不强，究其原因主要是学生在小学数学课堂并未摆脱应试教学的束缚，教师在教学中依然以考试为价值定向，忽视了数学建模思想的渗透，使得学生在与数学沟通时出现了障碍，继而影响了教师教学质量的提升和学生思维能力的开发。因此在教学中，教师应以学生熟悉的生活化的情境为切入点，充分调动学生参与学习的积极性，培养他们主动探究的好习惯，从而让他们在经历中更好地理解数学、理解教学，自然形成数学模型思想。

（1）模拟演示，体验“最优”方案

师：想一想，改进方案后，需要多长时间呢？（学生沉思）

师：这个好像是有点复杂，现在我们一起模拟一下打电话的过程，你们愿意吗？

学生齐声答：愿意。（听说要模拟演示，学生个个精神百倍）

师：很好。为了便于观察现在我们来确定一下规则。首先15人站成一排，接到电话后就需要转换身份，变为知情人，这时知情人请站在另外一排。

规则讲好后，有些学生还并未完全理解，教师先选择5个人表演，学生通过启发、提醒弄明白了游戏规则。接下来教师选择16人上台表演，指定1人为队长，其他学生为待通知的队员。有了前面的演练，学生很快完成角色的转换。

师：通过刚刚的实验，请大家思考一下，2分钟可以通知几人？3分钟可以通知几人？4分钟呢？

生11：2分钟可以通知4人；3分钟可以通知8人；4分钟可以通知16人。

师：很好，通过上面的实验你有什么发现呢？

生12：后一次通知的人数与知情人的人数相同。

生13：后一次知情人刚好是前一次知情人的2倍。

师：很好！通过刚刚的表演和推算，通知15人需要几分钟呢？

生齐声答：4分钟。

师：很好，这样我们的方法进一步得到了优化，由原来的7分钟缩短到了4分钟。

（2）画图演示，抽象模型

师：刚刚我们是通过“游戏法”完成了方案的优化。游戏法虽然很直观、很生动，不过它有很大的局限性，我们能否将刚刚的游戏过程换个形式来表达呢？

生14：可以用画图法。

师：很好，不过应该怎么“画”呢？请以小组为单位，探究一下，如何画最合理、最清晰。

学生以小组为单位积极交流，共同探究“最优”方案，几分钟后，有的小组已经完成了画图，教师选择两个有代表性的图示让学生上台展示并讲解。

师：结合图形和讲解，你是否理解了这两种画法具体表达的含义了？

学生齐声答：理解了。

师：很好，两种画法你更喜欢哪个呢？

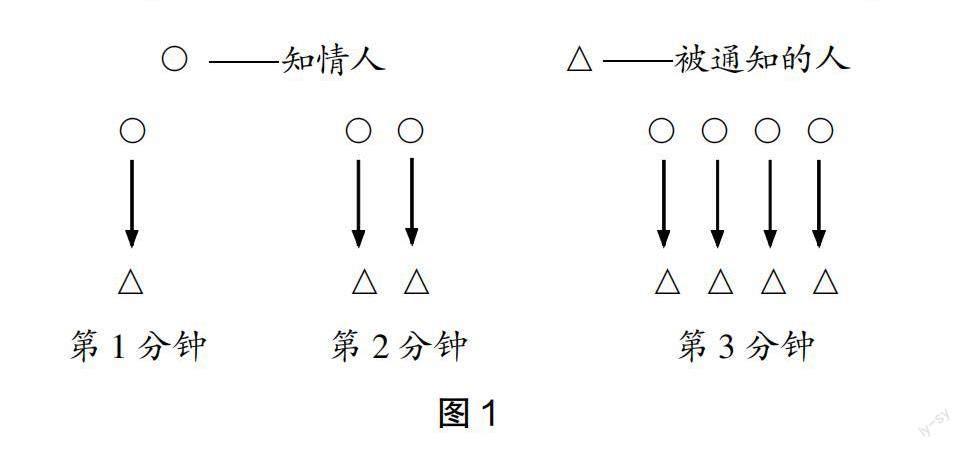
生15：我比较喜欢图1的画法，它与我们刚刚游戏的过程正好一致。

生16：我也喜欢图1，清晰、直观，更容易发现蕴含的规律。

生17：是的，图2看得有些眼花缭乱。（生17补充）

师：看来大家意见很统一。确实，图1表达得更加清晰，完美地呈现了一一对应关系，更易于理解和发现规律。

（3）探究规律，逐渐深化

师：利用画图法表达虽然直观、简洁，但是需要花费较多的时间，我们必须要找到一种更简洁的方法来表达，想一想有没有更好的方法呢？

生18：可以用算式来表达。

師：很好，现在我们结合图1分析一下，看看我们能找到怎样的数量关系呢？

师：第1分钟开始的时候共有几个人接到通知了呢？

生齐声答：1人。

师：1分钟结束后，变成了几人呢？

生齐声答：2人。

师：现在是原来的几倍呢？（用算式表达）

生齐声答：1×2倍。

师：第2分钟结束后，接到通知的有几人？

生齐声答：4人。

师：现在是原来的几倍呢？（用算式表达）

生19：1×2×2倍。

师：按照这样的规律，4分钟后，接到通知的共有多少人？又如何用算式表达呢？

生20：16人，算式为1×2×2×2×2。

师：想一想，这里面的“1”代表的是什么呢？（生沉思）

生21：代表第1个得到通知的人。

师：假如有4个人同时得到消息，你知道4分钟后共有多少人收到通知吗？

生22：就将算式中的“1”变成“4”，即4×2×2×2×2=64（人）。

师：真棒，看来大家已经弄清了问题的来龙去脉。

师：在实际打电话的过程中，为了确保“最优”方案的顺利实施，我们需要注意什么呢？

生23：要提前设计好流程图，确定好谁通知谁，这样才能做到不重复、不遗漏。

师：说得非常好，大家想问题想得真周到。

在建构模型、探究规律的过程中，教师不惜花费大量的时间带领学生亲身体验，并在亲身体验的过程中去抽象、去提炼、去优化，从而帮助学生认清了问题的实质，逐渐建构起“最优”模型。

4. 应用模型，稳固提升

练习是检测学生实际掌握情况的必经之路，是引导学生感悟“学以致用”教学价值的有效手段，为此，教师有必要精心设计一些练习帮助学生来检测知识、巩固知识，从而深化理解，便于学生更好地认识知识，提升解题技能。

师：既然大家掌握了“最优”方案，并建立了数学模型，现在大家想不想尝试用它来解决其他的实际问题呢？（经历了刚刚的探究，学生信心满满，迫不及待地想去体验一番）

问题1：某合唱团共有50人，在春节期间接到了一个紧急演出任务，团长若通过打电话的方式通知大家，每通知1人用时1分钟，请问最少多长时间能够通知完成？

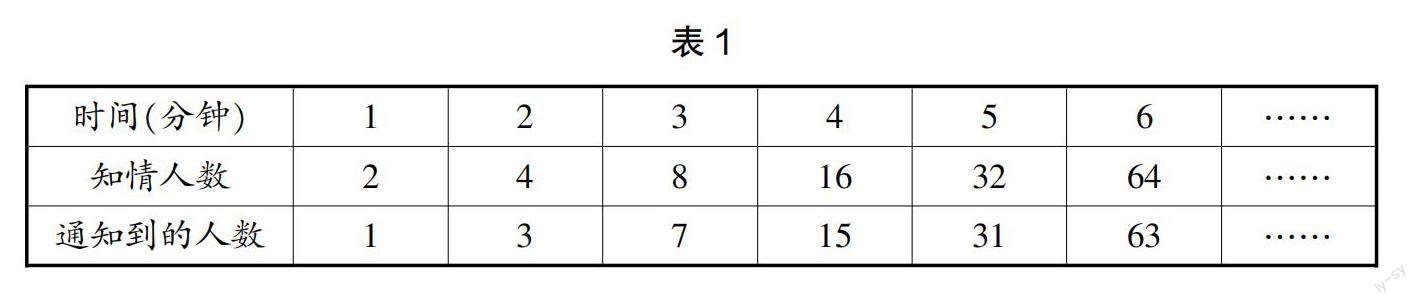
有了前面的探究经验，学生很快得到了答案。从学生的反馈来看，学生对列算式求解已经了如指掌了。为了进行有效的拓展和延伸，教师又鼓励学生尝试用其他形式来表示，在教师的引导下，学生又想到了应用表格法来表示，如表1。

通过表1，学生可以清晰地知道，若要通知16人到31人，需要5分钟，若通知的人数是32人到63人，则需要6分钟。

师：生活中类似的案例有很多，只要多观察、多探究，就会发现数学的无限魅力。

在练习阶段，学生熟练地应用模型解决了问题，为了有效拓展和延伸，在图形法、算式法的基础上，教师又指导学生应用表格法进一步体验模型，感悟一一对应关系。

5. 总结归纳，认识升华

在完成相应的练习后，教师鼓励学生进行总结归纳。教师耐心听取学生的反馈，并进行总结、归纳和补充，内容如下。

（1）为了节省时间，提高通知效率，可以让尽量多的人参与进来，例如在打电话通知时，让每个知情人都参与打电话可以有效缩短通知时间。

（2）打电话所反映的数学实质是一一对应关系。

（3）有时候“最优”方案在生活中并不具备可操作性，因为在实际生活中，很难提前预设好这个一一对应关系，即使提前制定好流程图，但是在实施过程中难免会遇到一些突发情况，这样就会使这种对应关系发生中断。不过，在现实生活中，研究打电话“最优”方案所建构的数学模型却有着广泛的应用价值，例如在认识和理解细胞分裂、传染病扩散等现实问题时，往往需要这类模型。

通过总结、归纳、反思，教师带领学生回顾模型，不仅使打电话的数学实质变得更加清晰，而且也让学生对模型有了更清晰的认识。同时，教师通过有效的补充，让学生体会到“最优”不一定是“最实用”的，应根据实际情况灵活应用“最优”方案。

二、教学反思

在教学中，教师以学生的认知为起点，借助生活情境引导学生在解决实际问题的过程中更好地认识数学、理解数学，使数学课堂既有浓厚的生活味，又不缺失厚重的数学味，整个教学过程自然、和谐。以上教学过程有以下两个亮点。

第一，重难点突出。整个过程紧紧围绕“最优”方案展开，学生凭借已有经验给出了“逐一打”和“分组打”两个方案后，教师又启发和引导学生对方案进行比较分析，从而联想到让更多的人参与进来。这样看似平淡无奇的过程，却激发了学生探究数学的热情，让学生在探究“最优”的过程中发现了最本质的东西，最终建构起了数学模型，顺利突破了教学难点。

第二，关注学生发展。在教学过程中，教师借助生活情境，激发了学生探究“最优”的迫切感、责任感和积极性。整个过程教师“以生为主”，通过“表演—画图—列式—建表”的过程，逐渐引导学生完成了模型的提炼。在此过程中，学生积累了数学活动经验，培养了数学学习热情，提升了数学思维能力。

总之，教师在备课时应该深思熟虑，既要尊重课堂生成，又要做好引导，促使学生有效提升数学思维能力，培养数学思维习惯，建立情感价值观念。