运用综合解题思路解答多项选择题的探索
2023-11-25钱宁
钱宁


摘要:所谓综合解题思路,就是面对难度较大的多项选择题时,要集中联系、分析、判断、推理于一体,以某一种解题方法为主,同时综合运用比较、计算、作图、验证、排除等多种方法,以达到“准确、快速、灵活、巧妙”解题的目的.
关键词:数形结合法;公式计算法;各个击破法;综合处理
选择题具有“小巧灵活、概括性强、知识覆盖面广、考查容量大、数学思想丰富、解题思路广、有一定的综合性与深度”等特点[1],是每年高考的重点题型,在高考试卷中数量大,占分比例高,全国卷和部分自主命题省份的高考试卷中选择题占60分(单项选择题40分,多项选择题20分).其中,多项选择题是近年来全国高考卷中出现的一种新题型,以2022年新高考卷为例,共设4个小题,每小题5分,共20分;在每小题给出的A,B,C,D四个选项中,有多项符合题目的要求,要全部选对才能得5分,部分选对只能得2分,只要有一项选错就不得分(0分).在单项选择题中,只需要在四个选项中选一个正确答案即可,而在多项选择题中,要在四个选项中,选出多个答案,而且要全部选对才能得满分.从上述的给分标准和答题的要求来看,其难度可窥见一斑!当然,无论是从试题的整体难度、选项的迷惑性,还是从筛选的复杂性等相比较,多项选择题的解答远比单项选择题麻烦,难怪许多考生面对多项选择题会发出“得分不易失分易”的槪叹.
不管是单选题还是多选题,它们都是选择题,其解法既有区别又有联系.当然,解答一些较复杂的多选题时,往往需要综合运用几种方法.下面重点探索如何运用综合解题的思路来解答多项选择题.
1 数形结合法
例1 (2022年新高考Ⅰ卷第9题)已知正方体ABCD-A1B1C1D1,则().
A.直线BC1与DA1所成的角为90°
B.直线BC1与CA1所成的角为90°
C.直线BC1与平面BB1D1D所成的角为45°
D.直线BC1与平面ABCD所成的角为45°
解析:如图1,连接B1C,BC1.因为DA1∥B1C,所以直线BC1与B1C所成的角即为直线BC1与DA1所成的角.因为四边形BB1C1C为正方形,则B1C⊥BC1,所以直线BC1与DA1所成的角为90°.
故选项A正确.
连接A1C,因为A1B1⊥平面BB1C1C,BC1平面BB1C1C,所以A1B1⊥BC1.
因为B1C⊥BC1,A1B1∩B1C=B1,所以BC1⊥平面A1B1C.又A1C平面A1B1C,所以BC1⊥CA1.
故选项B正确.
连接A1C1,设A1C1∩B1D1=O,连接BO.
因为BB1⊥平面A1B1C1D1,C1O平面A1B1C1D1,所以C1O⊥B1B.又C1O⊥B1D1,B1D1∩B1B=B1,所以C1O⊥平面BB1D1D.
因为C1C⊥平面ABCD,所以∠C1BC为直线BC1与平面ABCD所成的角,易知∠C1BC=45°.
故选项D正确.
故本题答案应选:A,B,D.
方法探索:以数形结合法为主,充分利用立体几何知识,通过作图、分析图形,综合使用观察、对比、验证、排除等方法依次对照选项进行筛选判断.
2 公式计算法
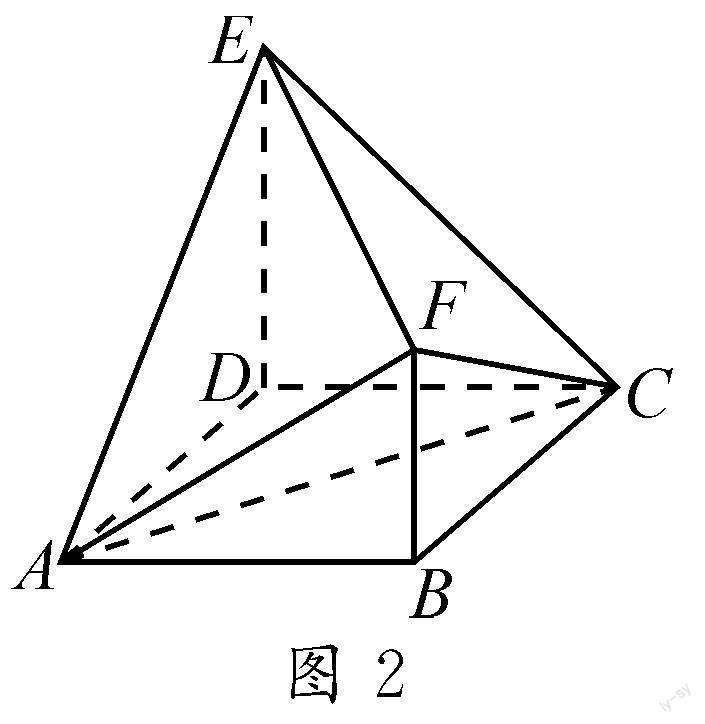
例2 (2022年新高考Ⅱ卷第11题)如图2,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则().
A.V3=2V2
B.V3=2V1
C.V3=V1+V2
D.2V3=3V1
解析:如图3,设AB=ED=2FB=2a,因为ED⊥平面ABCD,FB∥ED,所以
连接BD,交AC于点M,连接EM,FM,可知BD⊥AC.又因为ED⊥平面ABCD,AC平面ABCD,所以ED⊥AC.又ED∩BD=D,ED,BD平面BDEF,所以AC⊥平面BDEF.
综上,2V3=3V1,V3=3V2,V3=V1+V2.
把上述计算的结果与选项逐一对照,发现选项A,B错误,选项C,D正确.故本题答案应选:C,D.
方法探索:本题主要采用以三棱锥的体积计算结果与选项对照的方法进行判断,求解过程中还综合运用了作图(添加辅助线)、观察、证明、对照比较等方法.
3 各个击破法
例3 (2022年新高考Ⅰ卷第10题)已知函数f(x)=x3-x+1,则().
A.f(x)有兩个极值点
B.f(x)有三个零点
C.点(0,1)是曲线y=f(x)的对称中心
D.直线y=2x是曲线y=f(x)的切线
解析:根据题意可知,f′(x)=3x2-1.令f′(x)>
令h(x)=x3-x,该函数的定义域为[WTHZ]R[WTBX],h(-x)=(-x)3-(-x)=-x3+x=-h(x),
则h(x)是奇函数,点(0,0)是h(x)的对称中心.
将h(x)的图象向上移动一个单位得到f(x)的图象,所以点(0,1)是曲线y=f(x)的对称中心.故选项C正确.
令f′(x)=3x2-1=2,可得x=±1.又f(1)=f(-1)=1,则当切点为(1,1)时,切线方程为y=2x-1;当切点为(-1,1)时,切线方程为y=2x+3.故选项D错误,排除.
故本题答案应选:A,C.
方法探索:本题综合应用了定义法、比较法、验证法、代入法、分析法、排除法等多种方法,采用各个击破的策略,一种方法解决一个选项.首先根据极值点的定义判断A选项正确;再结合函数f(x)的单调性、极值等判断B选项错误;利用函数图象的平移判断C选项正确;根据导数的几何意义得出切线方程判断D选项错误.
从上述的解题探索中可以看出,多项选择题由于涉及到的知识点多,很难用单纯的某一种方法去解答,很多情况下需要运用综合处理的解题思路,直接方法与间接方法相结合,几种方法交替或同时并用[2],这样才有可能达到“又快又准”“小题小做”的目的.
参考文献:
[1]欧阳群壮.高考数学选择题的解答方法与技巧探析[J].中学教学参考,2016(23):28,103.
[2]杜雨轩.试析考试中如何快速解答高中数学选择题[J].数理化解题研究,2017(19):29-30.
