解无定法，但有法可寻

蔡宏梅

摘要：求解符合某种条件的动点运动规律问题，其实质就是利用题设中的已知条件，用“坐标化”将其转化为寻求变量间的关系；求轨迹方程的主要思路就是充分利用已知的几何条件，通过“解析化”将其转化为代数方程.本文中以研究2022年全国高考甲卷抛物线与直线方程大题的解法为切入点，通过相似题型的变式演练，探究了此类问题的常用解法.

关键词：真题展示；解法探究；思路分析；点评与总结

求抛物线与直线的方程是解析几何中最基本、最重要的问题之一，是用代数方法研究几何问题的基础.这类题目把基本知识、方法技巧、逻辑思维能力、解题能力融于一体，成为历年数学高考的高频考点与重点题型之一[1].

由于动点运动规律所给出的已知条件不同，因此求解方法也不相同，虽然解题的方法不固定，但是却有法可寻.下面结合高考真题来具体探究这类问题的思路与解法.

1 真题展示

例1 （2022年高考全国数学甲卷第20题）设抛物线C：y2=2px（p>0）的焦点为F，点D（p，0），过F的直线交C于M，N两点.当直线MD垂直于x轴时，|MF|=3.

（1）求C的方程；

（2）设直线MD，ND与C的另一个交点分别为A，B，记直线MN，AB的倾斜角分别为α，β.当α-β取得最大值时，求直线AB的方程.

2 解法探究

2.1 第（1）问的解法

所以抛物线C的方程为y2=4x.

点评与总结：定义法是求抛物线方程最常用的一种方法.

2.2 第（2）问的解法

點评与总结：解决第（2）问的关键是利用抛物线方程对斜率进行化简，最后利用韦达定理即可得出坐标间的关系.

3 变式演练

（Ⅰ）第（1）问的解法

（Ⅱ）第（2）问的解法

由第（1）问可先求A，B两点的坐标，用λ表示出点C，代入求值即可.

整理得（2λ-1）2=4λ+1，解得λ=0或λ=2.

点评与总结：解决此类问题通常采用“设而不求”的方法，首先设出直线与抛物线两交点的坐标，根据抛物线的方程正确表示出焦点弦长，再利用已知条件求解.

思路分析：先将|MN|转化为焦半径|AF|，|BF|的关系式，再变形，应用基本不等式即可求最大值.

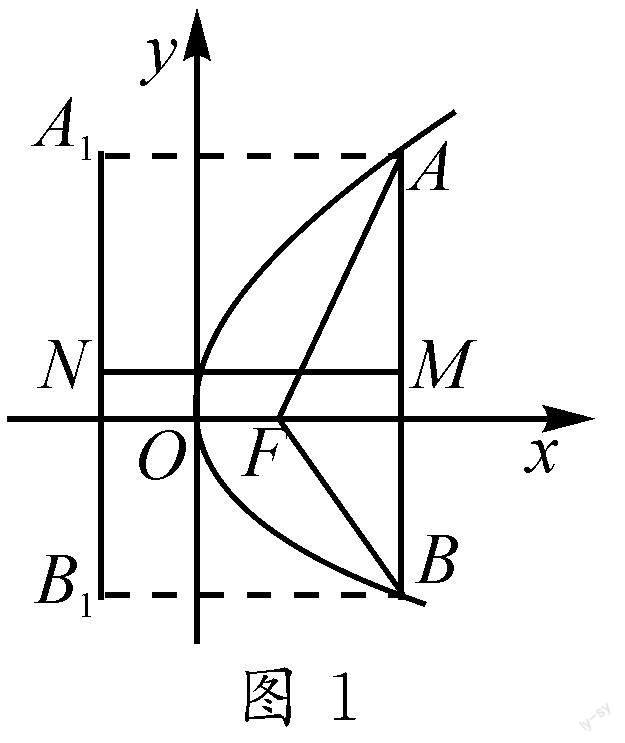
解析：如图1，过点A，B分别作抛物线准线的垂线，垂足分别为A1，B1.由题意，可知

综上所述，求解抛物线与直线的有关运动规律类问题，虽然没有可套的通用模式，但是有灵活的方法可寻.大多要经过审题、寻找并确定求解途径、逐步转化推演、综合陈述、完整作答或给出恰当的结论等必不可少的环节[2].在具体的解题过程中，在积极寻找恰当方法的同时，还要注意挖掘一些隐含条件，注明x，y的取值范围；要针对轨迹的不同情况，分别讨论，确保解题的完整性.

参考文献：

[1]谭著名.寻找解析几何解题的突破口[J].高中生，2011（15）：22-24.

[2]朱细秀.一道高中联赛解几试题的结论探源[J].中学数学研究，2015（4）：45-46.