三轴正交组合线圈结构参数优化设计

赵子豪,张永顺,郭小熙,董 海

(大连理工大学高性能精密制造全国重点实验室,辽宁 大连 116024)

0 引言

传统多自由度运动关节系统通常存在机械奇点、效率低、响应缓慢和动态性能变差等问题[1]。利用球型电机直接驱动的关节系统可以简化关节的复杂度,提高其动态性能和控制精度,同时缩小关节的体积。其中,基于永磁式球型电机[2-3]的电磁驱动球形关节具有占用空间小、系统效率高、磁能积高和转矩密度较高等特点,受到国内外学者的极大关注。

目前,研究人员提出了多种永磁球型关节结构和理论,现有永磁球型关节的定子绕组一般采用多个圆柱形空心线圈组成,通过冗余输入电流产生复杂磁场驱动转子运动,如Lee等[4]设计的变磁阻球型关节,定子为11个绕组线圈,转子为5个磁极;Kang等[5-6]提出了三自由度永磁球型轮式关节,转子由4个均匀分布的永磁体组成,定子分为2层,每层均分布6个线圈;Chai等[7-9]提出了一种定子分层设计的永磁球型关节,关节由球形转子和3层定子构成,球形转子上嵌有20个圆弧状永磁体,每层定子上开有21个定子槽。但过多的定子绕组使球型关节内部三维电磁场十分复杂,电流计算工作也具有挑战性,精确控制难度大。

为在电磁驱动球型关节磁场建模精度和稳定控制2方面取得实质性突破,本文在实现空间万向旋转磁场数字化控制基础上,依据空间万向旋转磁场的旋转定轴效应驱动原理,提出一种新型电磁变刚度球型手腕。

目前,均匀的空间万向旋转磁场一般采用三轴正交亥姆霍兹线圈叠加产生[10-11],实际应用的亥姆霍兹线圈外廓形状有圆形、正方形、正六边形以及八角形,但三轴正交亥姆霍兹线圈结构不够紧凑,装配后集成度低,无法满足球型手腕关节需求。

为了实现球型手腕的实际应用,需要设计新型的驱动线圈。鞍形线圈也可以在内部产生均匀稳定的磁场,可用于叠加产生空间万向旋转磁场,且鞍形线圈输出能量密度更高。将鞍形线圈与圆形亥姆霍兹线圈组合,得到了一种三轴正交组合线圈,线圈由内部2对正交鞍形线圈及外部1对亥姆霍兹线圈组成,线圈为嵌套紧凑结构,便于球型手腕设计。但现阶段对三轴正交组合线圈的研究很少,缺少面向新型电磁变刚度球型手腕的三轴正交组合线圈结构设计和参数优化方法。

本文针对三轴正交组合线圈的结构优化设计展开研究。

1 球型手腕结构

电磁驱动球型手腕结构如图1a所示,包括三轴正交组合线圈和随动机构。图1b的三轴正交组合线圈由内部2对正交鞍形线圈及外部亥姆霍兹线圈紧凑嵌套组成;随动机构包括外部十字万向节、NdFeB(钕铁硼)永磁体转子、固定端、输出端以及电磁制动装置。手腕采用多层嵌套,随动机构结构紧凑、转动灵活,可实现2个自由度的运动解耦、测量与控制;三轴正交组合线圈结构紧凑,磁场均匀区域大,能量输出密度大。

图1 电磁驱动球型手腕结构

2 模型建立

2.1 磁感应强度建模

根据 Biot-Savart 定律,单轴线圈的中心磁感应强度为

Bi=Ki·Ii

(1)

Ii(i=1,2,3)分别为通入线圈1、线圈2和线圈3中电流,设I0(取值9 A)为线圈电流幅值;Ki(i=1,2,3)分别为线圈1、线圈2和线圈3的结构系数,其表达式为:

(2)

(3)

(4)

其中,真空磁导率μ0=4π×10-7H/m;Ni(i=1,2,3)分别为线圈1、线圈2和线圈3的匝数。Ni、Ci、Di、Ei、Fi(i=1,2,3)表达式为:

(5)

(6)

(7)

(8)

(9)

kη为导线排绕系数(取值1.05);kβ为导线叠绕系数(取值1.15);d0为带有漆包线的导线直径(取值0.85 mm)。

内鞍形线圈1、外鞍形线圈2和外亥姆霍兹线圈3依次嵌套组成三轴正交组合线圈,线圈结构如图2所示,2Hi(i= 1,2,3)为各线圈总高;2h1、2h2为内外鞍形线圈上下圆弧导线段的距离;2h3为亥姆霍兹线圈距离;Ri、ri(i= 1,2,3)分别为各线圈外侧、内侧半径;φ1、φ2为内外鞍形线圈竖直导线段外侧张角;θ1、θ2为内外鞍形线圈竖直导线段内侧张角。

图2 三轴正交组合线圈结构

2.2 球型手腕输出力矩建模

为实现球型手腕输出力矩的解耦计算,建立坐标系对手腕运动过程进行描述,如图3所示。

图3 手脓包运动过程描述

O-XYZ为电磁变刚度球型手腕固定坐标系,坐标原点在线圈组的中心;o-x0y0z0为平动坐标系,坐标原点在永磁体转子中心;o-x1y1z1为跟从随动部分摆动的赖柴坐标系,是由坐标系o-x0y0z0绕y0轴旋转α角得到中间坐标系o-x1y1z1,再绕x1轴旋转β角后得到。根据上述坐标系,球型手腕任意时刻的摆动角度可由侧摆角和俯仰角,即(α,β)确定。

假设初始位置旋转磁场法向量nB与球型手腕输出轴的轴线nm重合,并在固定坐标系O-XYZ内竖直向上,则在固定坐标系下旋转磁矢量BH为

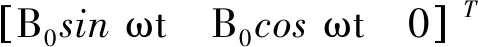
(10)

B0为旋转磁场磁感应强度;ω为旋转磁场的角速度。球型手腕内部永磁体磁矩矢量m在固定坐标系O-XYZ下可表示为

m=[m0sin(ωt-δ)m0cos(ωt-δ) 0]

(11)

m0为永磁体磁矩值;δ为转差角。

控制电流使旋转磁场法向量nB在固定坐标系中侧摆角为0,俯仰角为β,此时旋转磁矢量B1在固定坐标系O-XYZ内可以表示为

B1=A·BH

(12)

A为相应的齐次变换矩阵,具体为

(13)

根据磁力矩耦合公式T=m×B1,联立式(10)～式(13),最终耦合磁力矩T在固定坐标系O-XYZ下为

(14)

Tx、Ty、Tz均为周期函数,通过周期等效控制力概念的引入,可对周期力进行简化[12]。则单个周期内三轴的平均磁力矩为

(15)

一般情况下转差角很小,取手腕转差角等于0,此时球形手腕平均磁力矩为

(16)

此时旋转磁场法向量nB与球型手腕输出轴的轴线nm之间的夹角为β,手腕平均磁力矩是驱动永磁体的主要力矩,磁力矩的大小与nB、nm之间的夹角有关,且永磁体在磁力矩的作用下始终具有跟随旋转磁矢量法线方向的趋势,即旋转定轴效应。

3 优化设计指标分析

电磁驱动球型手腕内置永磁体如图4所示。依据旋转定轴效应,空间万向旋转磁场同轴随动磁矩直接驱动永磁体实现手腕的俯仰、侧摆运动,空间万向旋转磁场的均匀区域需要时刻包围着运动的永磁体,手腕的输出力矩才能达到最大,因此,永磁体体积V应当小于磁场均匀区域体积Ve,设空间内某点磁感应强度与线圈中心点磁感应强度偏差值e≤1%的空间区域为磁场均匀区,那么永磁体体积应为

图4 永磁体结构

(17)

其中,永磁体半径Rm=0.3r1,高度Hm=0.41H1[13]。

永磁体的磁矩值为

(18)

Br为牌号N52的永磁体剩磁;V为永磁体体积。联立式(16)～式(18),可得手腕的最大输出力矩应为

(19)

由式(19)可知,球型手腕的输出力矩与线圈的结构参数有关,也和内部永磁体的体积有关。永磁体的体积与线圈1的尺寸直接相关,同时三轴正交组合线圈由内而外依次嵌套装配,如图2所示。线圈1结构参数直接影响三轴正交组合线圈所占空间体积,因此,首先优化设计鞍形线圈1,再以线圈1为标准,设计线圈2、线圈3。设计过程如下所述。

a.鞍形线圈1的优化设计是一种多目标优化问题,既要使球型手腕的输出力矩最大,又要缩小线圈1所占的空间体积,在对线圈1设计时,球型手腕的输出力矩为

(20)

线圈1所占空间体积V1为

(21)

综上所述,线圈1优化目标函数为

(22)

优化参数:H1,h1,R1,r1。

约束条件如下所述。

正常装配的鞍形线圈1尺寸满足:

r1>0,R1>r1,H1>h1

鞍形线圈1生成空间万向旋转磁场均匀区最大时,线圈尺寸应满足:

(φ1+θ1)/2=120°,(H1+h1)/(R1+r1)=2

b.根据设计的线圈1,对线圈2与线圈3进行单目标优化设计,线圈2优化目标函数为

(23)

优化参数:H2,h2,R2,r2。

约束条件如下所述。

与线圈1结构系数匹配并嵌套装配的线圈2尺寸满足:

K2=K1,r2>R1,R2>r2,H2>h2

线圈2生成空间万向旋转磁场均匀区最大时,线圈尺寸应满足:

(φ2+θ2)/2=120°,(H2+h2)/(R2+r2)=2

c.线圈3优化目标函数为

(24)

优化参数:H3,h3,R3,r3。

约束条件如下所述。

与线圈2结构系数匹配并嵌套装配的线圈3尺寸满足:

K3=K2,r3>R2,R3>r3,H3>h3

线圈3生成空间万向旋转磁场均匀区最大时,线圈尺寸应满足:

(R3+r3)=2(H3+h3)

(25)

4 优化求解

NSGA-II算法通过将待优化问题转换为二进制数码串(个体),同时随机产生一群码串(种群)置于求解的编码空间中。根据适者生存原则,从种群中选择出对环境适应能力较强的个体进行交叉和变异操作以产生新一代更能适应环境的个体。新个体继承上一代个体的优秀基因,性能更优于上一代个体。再从新个体中选出优秀个体进行下一代进化,经过不断进化,种群向最优解不断靠近最后收敛于1个解集,便求得Pareto最优解。Pareto最优解表示在1个解空间中的1个解向量X,如果没有任何1个解向量能够支配该解向量X,就把该解向量称为此优化问题中求得的Pareto最优解。

NSGA-II算法的一般过程为:首先,随机生成1个包含N个体的种群即父代种群,计算个体拥挤度,并对父代种群当中的个体进行非支配排序;然后由个体拥挤度大小决定所在层级,选出适当的个体投入交配池中对池中的个体进行交叉、变异等操作产生新的下一代种群;最后,进行精英策略操作把所得的N个体作为新的父代继续重复上述过程,直至达到终止条件,流程如图5所示,算法的约束条件设置如表1所示。

表1 算法约束条件

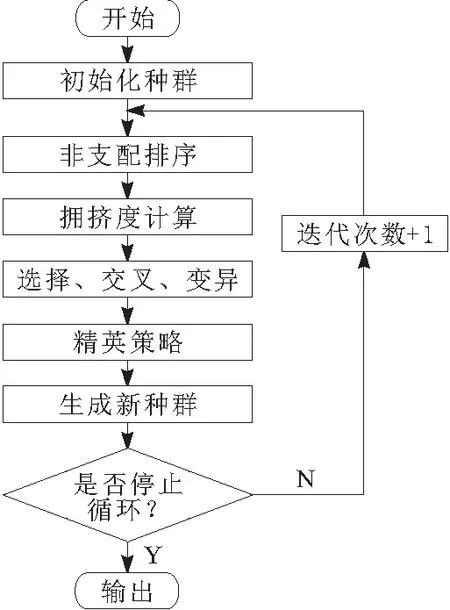
图5 算法流程

算法以手腕输出力矩和线圈1所占空间体积为最优解目标,获得Pareto最优解集在保证手腕输出力矩能够实际应用的前提下,考虑以体积较小为目标,选择线圈1结构参数的优质解。

线圈2、线圈3为单目标优化,以线圈1为标准可以设计得到线圈2和线圈3的结构参数具体值, 根据实际三轴正交组合线圈匝数为整数以及球型手腕装配和性能的要求,需要微调优化数据,最后得到各线圈参数如表2所示。

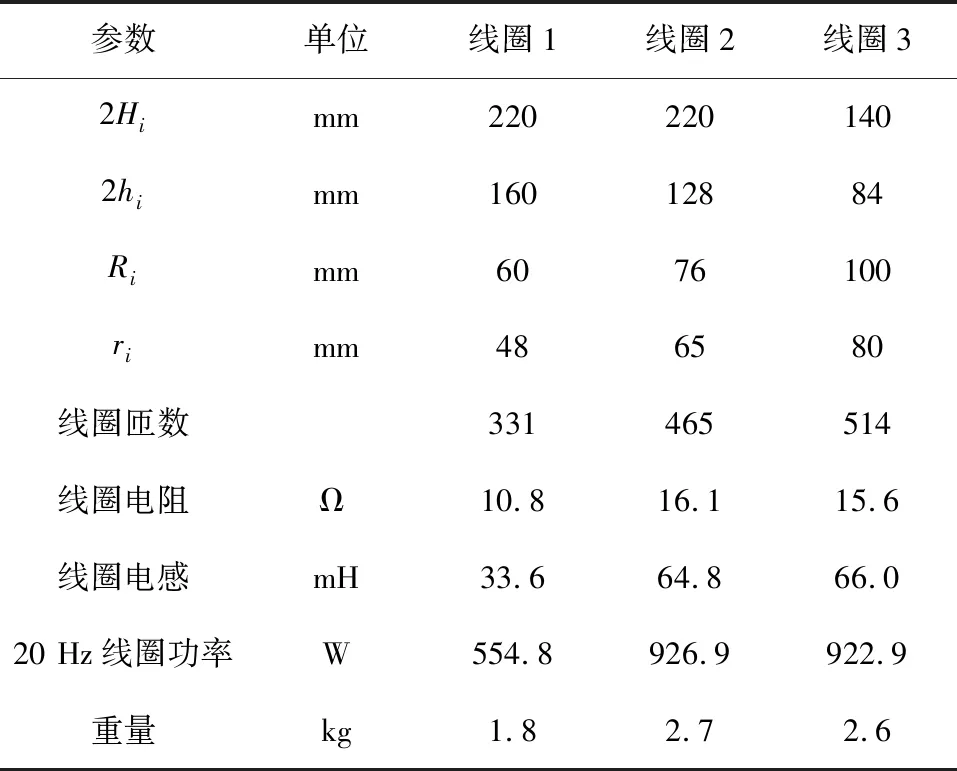
表2 线圈结构参数

5 仿真与试验验证

根据表2线圈结构参数,结合式(2)～式(4)可求得线圈的结构系数为K1=4.38×10-3,K2=4.42×10-3,K3=4.40×10-3。

向三轴正交组合线圈通入电流幅值为I0(取值9 A)的电流,线圈内可生成磁感应强度为39.6 mT的空间万向旋转磁场。

为验证三轴正交组合线圈可以生成空间万向旋转磁场,研制了电磁变刚度球型手腕样机以及试验平台,如图6所示。试验平台由上位机、控制器和变压器组成,在试验中,通过绝对编码器测量手腕摆动角度,使用传感器测量球型手腕在不同磁场参数下输出的力矩,并通过录像机全程采集手腕运动信息。

图6 球型手腕试验平台

如图7所示,向三轴正交组合线圈中通入可以产生磁场轴线侧摆角、俯仰角为(10°,0)的电流,同时切断电磁制动,手腕轴线开始向着磁场轴线运动,由图7a的初始状态,在耦合磁力矩的作用下,经过图7b和图7c,最终稳定在图7d的目标方位,并在目标方位处由空间万向旋转磁场驱动内置永磁体转子稳定旋转。

图7 球型手腕运动过程

由于空间万向旋转磁场很难直接检测,本文采用仿真分析线圈磁场均匀度。进行仿真验证时,仿真参数如表3所示。

表3 仿真参数

由于三轴正交组合线圈由内外鞍形线圈和圆形亥姆霍兹线圈嵌套组成,为了充分分析线圈内磁场的分布情况,取图8所示坐标系X-O-Y、X-O-Z和Y-O-Z截面分析磁场均匀性,同时取时间点t=0.2 s,对磁场的相对误差分布图进行仿真。

图8 线圈截面

图9为磁场偏差等值线图,图中白色区域为与中心的磁场强度偏差e≤1%区域。随着仿真截面不同,图9a～图9c磁场均匀性分布也不相同,因此,线圈内部均匀磁场大小应为不同截面均匀区域的共有空间范围,将该均匀区看作一个中心点在原点的圆柱体。

图9 t=0.2 s线圈内部磁场偏差等值线图

表4 各种线圈均匀区占比

三轴正交组合线圈均匀度是三轴正交方形亥姆霍兹线圈的1.57倍,是三轴正交圆形亥姆霍兹线圈的1.76倍[15]。

设计三轴正交亥姆霍兹线圈结构参数[14],保证其相同内部活动空间和磁感应强度与三轴正交组合线圈相同,三轴正交亥姆霍兹线圈参数如表5所示。

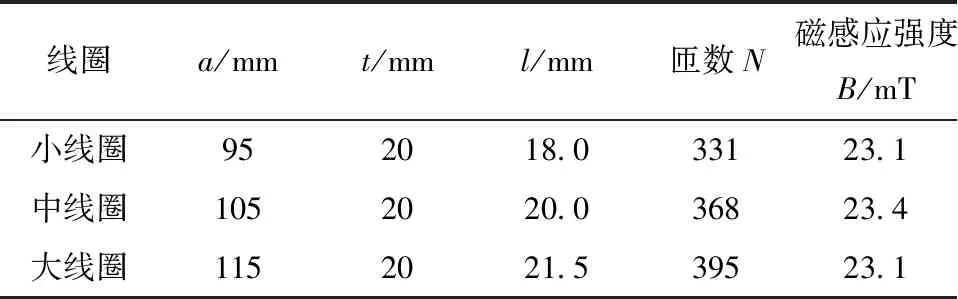
表5 三轴亥姆霍兹线圈结构参数

三轴亥姆霍兹线圈空间体积为0.011 4 m3,而三轴正交组合线圈所占空间体积为0.006 9 m3,中心点磁感应强度为39.6 mT。三轴正交组合线圈具有更大的旋转磁场均匀区,且线圈嵌套装配,空间利用率更高,磁感应强度更高,输出力矩更大。

6 结束语

针对电磁变刚度球型手腕对高集成度和高能量输出密度的实际需求,提出了组合线圈驱动方案,具体包括2组鞍形线圈和1组亥姆霍兹线圈。并根据建立的模型以手腕输出力矩和线圈空间体积为优化指标,基于遗传算法对三轴正交组合线圈优化设计,最终得到了最优的线圈结构参数。

通过计算与仿真验证三轴正交组合线圈性能,与三轴正交亥姆霍兹线圈对比分析,三轴正交组合线圈产生的旋转磁场均匀度更高(约为三轴正交方形亥姆霍兹线圈的1.57倍,三轴正交圆形亥姆霍兹线圈的1.76倍),并且在更小体积的情况下磁感应强度更大,具有更高的能量输出密度与集成度,更适用于电磁变刚度球型手腕。