基于Autogluon算法绳驱动手术器械运动补偿控制
2023-11-25牛国君汪巍巍朱姚俊
牛国君,汪巍巍,朱姚俊
(浙江理工大学机械工程学院,浙江 杭州 310018)
0 引言
机器人辅助微创手术与传统微创手术相比,具有手术器械自由度数多、操作灵活、手眼一致好及改变手术操作方式降低医生手术强度等优点,因此广泛应用于临床外科手术中[1]。受灭菌方式、无菌环境以及手术操作空间限制,手术器械前端的小爪驱动采用钢丝绳驱动,而钢丝绳受预紧力、摩擦力和滞回等非线性影响[2],无法建立准确钢丝绳数学模型,且手术器械前端不能安装传感器,无法形成全闭环控制,从而导致手术器械小爪的具体运动位置往往不准确,进而影响手术器械前端姿态和主手姿态的一致性。
针对该问题主要有2种解决方法,第1种方法是通过对钢丝绳进行传统数学建模,通过模型补偿方式来实现。如Naerum等[3]提出了一种钢丝绳指数刚度模型和库伦粘滞模型;Do等[4]提出了一种高效的滞回模型作为前馈用于柔性内窥镜系统中位置控制;Xu等[5]提出通过摩擦前馈补偿方法提高钢丝绳位置精度;Kosari等[6]提出了在绳驱动机构的控制系统中引入钢丝绳张力补偿来提高系统精度,但误差精度大约为5°;王文杰等[7]提出基于关节转角估计器的绳驱动手术微器械位置全闭环控制;Xue等[8]建立末端执行器张力和位移传递模型,通过前馈控制实现位置补偿;Palli等[9]建立粘弹模型来补偿钢丝绳非线性效应;Zhou等[10]提出了钢丝绳的直线位移模型,通过该模型进行补偿提高运动精度。但是该方法并不能很好描述一些非线性影响因素,故而导致位置估计不准确及位置补偿精度低。第2种方法是借助人工智能方法对采集数据进行学习,进而实现对钢丝绳运动位置补偿,该方法在描述和逼近非线性方面具有优势[11]。Xu等[11]提出了应用回归方法学习钢丝绳非线性特性,以提高钢丝绳驱动手术机器人运动精度;Mahler等[12]提出了应用高斯过程回归方法学习钢丝绳驱动手术机器人运动学模型,实现精确运动;Haghighipanah等[13]提出了应用无迹卡尔曼滤波提高钢丝绳驱动手术器械位置精度;Giorelli等[14]提出应用前馈神经网络学习非线性逆运动学模型,提高钢丝绳运动精度;Porto等[15]提出了应用机器学习方法提高绳驱动手术器械运动位置精度;Liang等[16]提出了基于支持向量机方法实现对绳驱动手术器械运动补偿。本文采用机器学习Autogluon[17]算法来实现对手术器械末端位置估计,并将该位置估计作为前馈来实现对手术器械末端的补偿控制,进而提高手术器械末端位置精度。
1 微创手术机器人手术器械
1.1 自由度配置
手术器械采用钢丝绳驱动,其末端共有俯仰、偏摆、开合和绕手术器械轴线回转4个自由度。简化机械结构,采取R-P-Y结构,即回转-俯仰-偏摆-开合的自由度配置。夹爪设计如图1所示。小爪的俯仰、偏摆和开合均由钢丝绳传动。
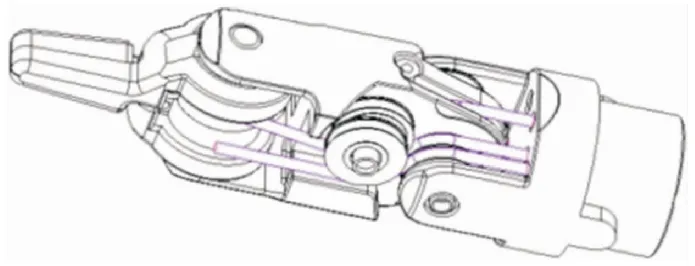
图1 手术器械末端执行器
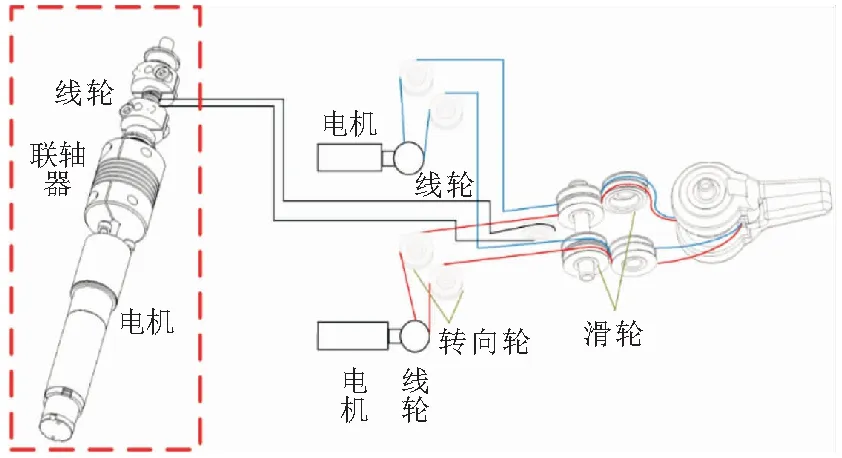
图2 手术器械钢丝绳传动

图3 钢丝绳迟滞效应
1.2 手术器械驱动方式
手术器械末端执行机构采用丝传动的方式,相比于齿轮传动,丝传动具有占用空间小、传动平滑和无传动间隙的优点,适合于机器人的末端执行机构。同时,丝传动也具有迟滞效应和传动不精确的问题。本文实验平台如图 2所示。
1.3 小爪的滞回特性
小爪运动过程中,电机运动曲线和小爪的运动曲线存在错位的情况,如图 3所示。其原因如下:
a.手术末端执行机构通常有较长的柔性传动距离,从电机到小爪的执行端通常有40~60 cm的钢丝绳传动距离。
b.为保证小爪能够有效传递电机的力,通常手术末端执行机构会设置较大的预紧力,因此在器械内部往往会有较大的摩擦力。
钢丝绳迟滞性不仅会降低系统的控制精度,还会产生与输入信号幅值相关的相移和谐波失真,从而降低了控制精度。钢丝绳迟滞性表现为:多映射、记忆性、非线性、非对称性和环中环。
常见的迟滞补偿方式分为3种:第1种是基于模型的前馈补偿方法,即建立小爪的摩擦力、动力学以及钢丝绳传动模型,把模型建出来后辨识,辨识后直接前馈补偿;第2种是采用传感器或者视觉[18-20]对小爪的运动位置进行实时的测量;第3种是采用机器学习的方法对小爪的状态进行辨识,同时对电机的运动轨迹和位置进行修正。本文采用第3种方法实现对手术器械小爪位置补偿。
2 手术器械末端执行器轨迹估计算法
2.1 位置估计实验平台设计
实验平台如图4所示,采用Maxon公司的DCX12L电机,GPX12A齿轮箱,传动比83∶1,电机编码器为ENX 10 EASY 1024IMP,驱动器是鸣志ipos-2401驱动器。本次实验测量电机的转动角度、转动速度、小爪两端绳位移、钢丝绳张力及小爪转动角度。采用欧姆龙E6B2-CWZ1X编码器测量电机和小爪的转动位移,采用天先数智科技公司的LMD2000增量式磁栅编码器测量钢丝绳位移。采用常州瑞尔特测控的拉力传感器测量钢丝绳张力,量程为500 N。上位机使用EtherCAT通信协议通信。钢丝绳采用DMC公司R45钢丝绳,最大负载200 N。直线导轨采用上银SSEB10G-95直线导轨。

图4 实验平台
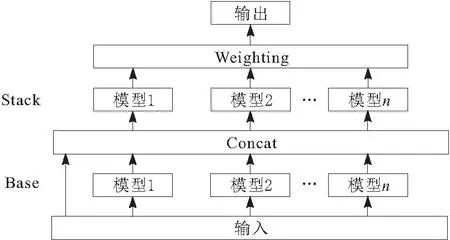
图5 Autogluon的多层堆叠模型
微器械单关节原理样机实验系统首先运用线轮调节预紧力,使系统处于预紧状态,位移传感器提供位移数据。线轮将电机的旋转运动转化为钢丝绳的直线运动,同时为小爪运动和负载提供动力。欧姆龙编码器用于修正电机转动的回程差,以及测量小爪旋转角度,小爪旋转角度的测量值用于修正电机对小爪转动角度的估计值。
2.2 手术器械末端轨迹估计
2.2.1 Autogluon机器学习算法
a.特征工程。
计算机无法区分电机的“正加速”、“正减速”、“负加速”和“负减速”这样分类,故采用“是不是正加速”、“是不是正减速”、“是不是负加速”和“是不是负加速”来分开表示电机的运动特征。采用独热向量编码对电机的不同运动特征加以区分。区分结果如表1所示。

表1 电机特征工程建立
b.集成学习。
集成学习面临着很多问题,如训练模型选择困难、超参数难以确定及训练时间长等。由于传统的集成模型等缺点,采用亚马逊设计的全新的机器学习训练框架Autogluon[17]模型。该模型主要采用多层堆栈融合、Bagging、Stacking及K折交叉验证技术,大幅提高集成模型的运算效率和估计精度,组合来自多个模型的集成优于单个模型,通常会大大降低最终预测的方差。
Autogluon采用常见的机器学习模型对1组单独的基础模型进行单独训练,随后,使用基本模型的聚合预测作为其特征来训练堆叠模型,堆叠模型可以改进单个基础预测的缺点,并利用基础模型之间的交互来增强模型的预测能力。
多层堆叠将堆叠器模型输出的预测作为输入提供给额外的更高层堆叠器模型。但是常见的多层堆叠过分依赖于系统的调参,往往稍作改动,模型就需要重新调参,调参费时费力,经常需要花费大量时间和计算资源同时需要具有专业知识和经验的数据工程师参与操作。
Autogluon引入了一种新的多层堆栈集成方式,如图 5所示。 第1层有多个基础模型,输出被连接起来,然后反馈送到下一层,它本身由多个堆叠器模型组成。这些堆叠器充当附加层的基础模型。
Autogluon通过2个方式改变来扩展传统的堆叠方法,以提高其结果的准确性。 Autogluon为了避免过拟合问题,采用比基础层更简单的模型。 Autogluon只是简单地将所有基础层模型堆叠,这种技术可以被视为一种利用分层训练的深度学习的替代形式,其中,层之间连接的单元可以是任意的模型。
2.2.2 基于Autogluon机器学习算法转角位置估计
当电机实际轨迹为正弦函数时,采用Autogluon对小爪实际轨迹进行估计,如图6得到小爪最大误差为0.43°,平均误差为0.028°。当电机实际轨迹为多项式函数时,采用Autogluon对小爪实际轨迹进行估计,如图7得到小爪最大误差为0.77°,平均误差为0.046°。

图7 基于Autogluon多项式转角估计预测误差
为验证Autogluon算法有效性,当电机轨迹为正弦函数和多项式函数时,分别应用线性回归、支持向量机、高斯过程、神经网络和决策树方法对小爪实际轨迹进行估计。
当电机轨迹分别为正弦函数和多项式时,基于线性回归对小爪实际轨迹进行估计,如图8和图9所示,最大误差分别为3.37°和2.96°,平均误差分别为1.14°和0.79°。

图8 基于线性回归三角函数转角估计预测误差
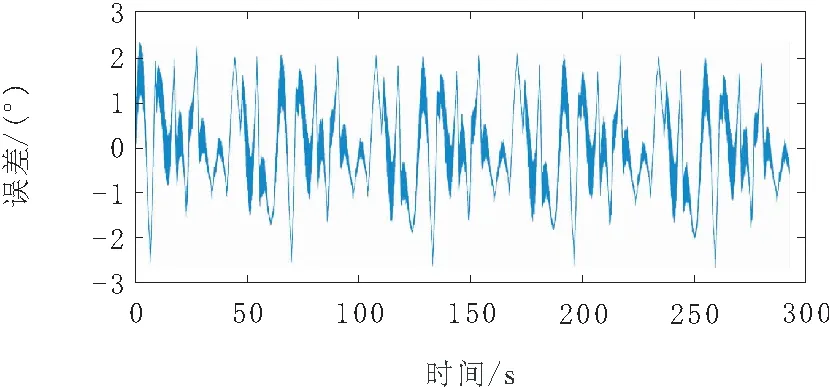
图9 基于线性回归多项式转角估计预测误差
当电机轨迹分别为正弦函数和多项式时,基于支持向量机对小爪实际轨迹进行估计,如图10和图11所示,最大误差分别为4.15°和2.28°,平均误差分别为1.95°和0.82°。
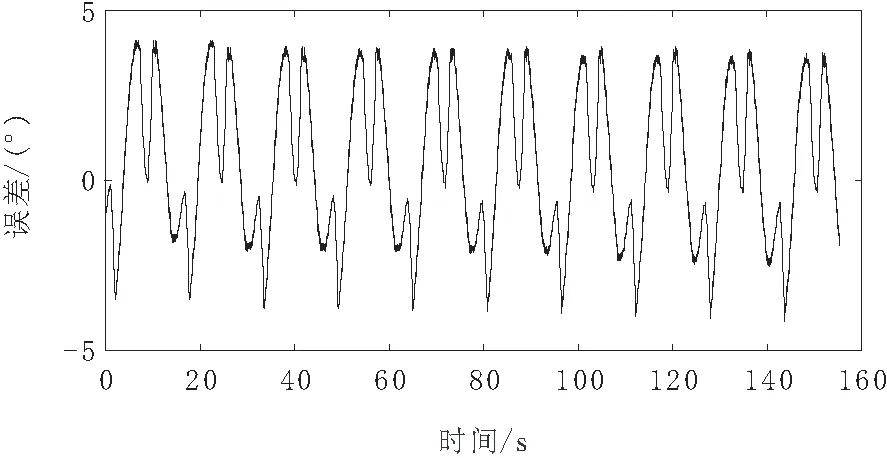
图10 基于支持向量机三角函数转角估计预测误差
当电机轨迹分别为正弦函数和多项式时,基于高斯过程对小爪实际轨迹进行估计,如图12和图13所示,最大误差分别为2.53°和1.21°,平均误差分别为0.13°和0.10°。
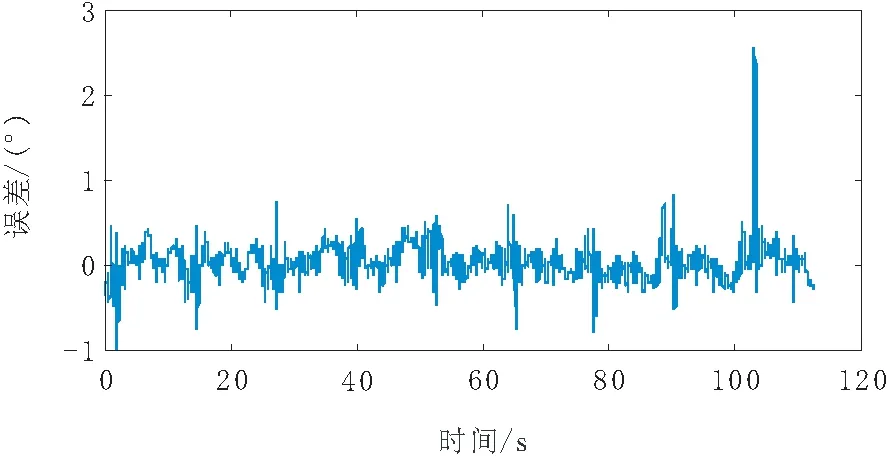
图12 基于高斯过程三角函数转角估计预测误差

图13 基于高斯过程多项式转角估计预测误差
当电机轨迹分别为正弦函数和多项式时,基于支持神经网络对小爪实际轨迹进行估计,如图14和图15所示,最大误差分别为0.66°和1.92°,平均误差分别为0.22°和0.39°。

图14 基于神经网络三角函数转角估计预测误差
当电机轨迹分别为正弦函数和多项式时,基于决策树对小爪实际轨迹进行估计,如图16和图17所示,最大误差分别为2.72°和2.74°,平均误差分别为1.11°和0.24°。

图16 基于决策树三角函数转角估计预测误差

图17 基于决策树多项式转角估计预测误差

图18 手术器械末端执行器运动补偿
将Autogluon和线性回归、支持向量机、高斯过程、神经网络和决策树5种方法相比较,分别测试末端运动预测均方误差(MSE)、平均绝对误差(MAE)、最大误差(ME)和标准差(SD)。对比结果如表2和表3所示,Autogluon方法的均方误差、平均绝对误差、最大误差和标准差4个指标最小,因此,Autogluon方法转角估计效果最好。

表2 当电机轨迹为三角函数时转角估计效果对比
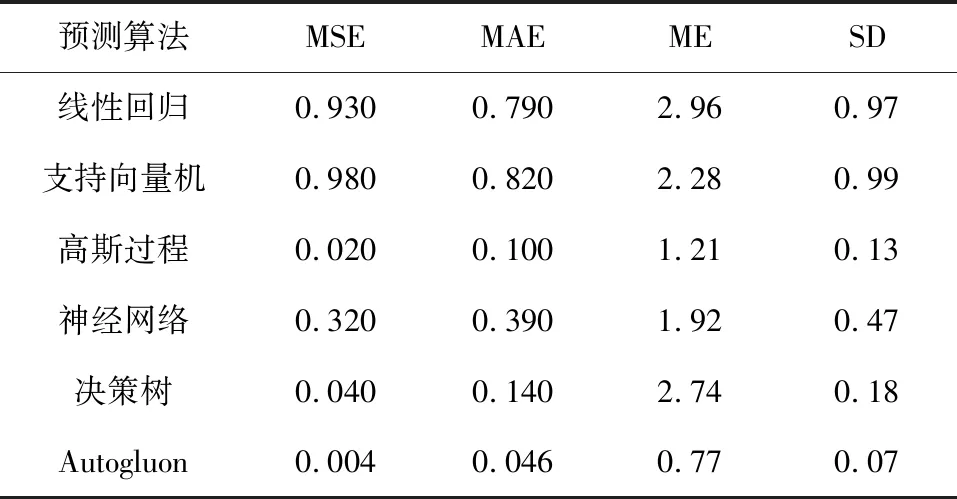
表3 当电机轨迹为多项式函数时转角估计效果对比
2.2.3 基于Autogluon机器学习算法转角位置补偿
根据手术器械的运动规律,采用反馈和前馈结合的方式解决小爪运动误差问题。 实验中,通过转向加速的方式进行前馈补偿,减小迟滞效应和电机的回程误差,同时用机器学习的方式计算小爪的运动误差,对小爪的运动进行补偿。补偿方式如图 18所示,将Autogluon和线性回归、支持向量机、高斯过程、神经网络和决策树5种方法相比较。6种补偿效果如表4所示。分别测试其转角补偿的均方误差(MSE)、平均绝对误差(MAE)、最大误差(ME)和标准差(SD)。Autogluon方法的转角补偿的均方差、平均绝对误差、最大误差和标准差4个指标最小,因此,Autogluon方法转角补偿效果最好。

表4 转角补偿效果误差对比
3 结束语
本文提出基于Autogluon算法手术器械末端执行器位置估计,与基于线性回归、支持向量机、高斯过程、神经网络和决策树相比,该方法位置估计精度最高。将基于Autogluon算法估计位置作为反馈对手术器械末端执行器运动进行补偿,与上述5种方法估计位置作为反馈进行运动补偿效果相比,该方法运动补偿效果最优,证明该方法有效。
