单侧受压密封圈摩擦力的建模与辨识

万 禹,张 波

(上海交通大学机械与动力工程学院,上海 200240)

0 引言

橡胶密封圈因其结构简单、安装便捷和成本低廉等优点,在工业实践中得到了广泛应用,如液压油缸、气缸、制动器/离合器的密封等[1-2]。密封圈的摩擦特性是密封领域研究的重要问题之一。密封圈在受到单侧的介质压力时会发生明显的单向变形,其摩擦特性受到影响,关于速度呈现不对称性。当前,国内外相关文献主要研究密封圈材质、几何尺寸、压缩率、介质压力、运动速度和润滑条件等因素对摩擦力大小的影响,通过优化密封圈的结构设计与选型、改善摩擦接触面润滑条件和调整介质压力等方式降低密封圈摩擦力,提高机构性能。刘莹等[3]研究了不同润滑条件下密封圈摩擦系数的变化;李双喜等[4]分析了密封圈压缩量及滑移速度对摩擦力的影响;吴琼等[5-6]测量了O型密封圈摩擦力,但测试速度较低,主要研究了启动过程的动态特性;朱启惠等[7-8]和朱得磊等[9]讨论了氟橡胶O型密封圈粘滞、回弹和微动等摩擦学行为特性;童悦等[10]研究了运动速度对密封圈摩擦力的影响,发现其随着速度的增加而增大;姚春峰等[11]分析了不同边界条件下的O型密封圈等效应力、接触应力和剪切应力等,得到了上述因素之间的变化关系;肖士珩[12]对O型密封圈进行应力和应变分析,从理论上计算了其摩擦力;Tadic等[13]研究了高真空度下气缸密封圈的摩擦力,发现真空度越大摩擦力也越大;Wang等[14]探究了活塞杆速度、颗粒尺寸和颗粒质量分数等对密封圈摩擦力的影响规律;Aghdasi等[15]发现密封圈摩擦力在边界区、混合润滑区、流体动力区以及预滑动区均存在滞回现象。

上述研究均假设密封圈两侧压力对称,或假设不对称的压力不会影响摩擦力的对称性。然而实际应用中密封圈主要工作在单侧受压的工况,如气缸中密封圈两侧分别受高的介质压力和大气压力作用。这种不对称的压力导致了密封圈摩擦力的不对称,而目前对此的相关研究较少。桑建兵等[16]分析了单侧受压O型密封圈的大接触变形,发现随介质压力的增加,密封圈接触宽度和接触应力的峰值也明显增加;Raparelli等[17]探究了高压下Y型密封圈的挤出现象,并测量了单向摩擦力;迪力夏提·艾海提等[18]研究了单侧受压Y型密封圈向不同运动方向时的摩擦力,发现外行程方向的摩擦力显著大于内行程方向。这些文献完成了单侧受压密封圈摩擦力的测量,但并未对摩擦力进行建模与辨识,无法用于控制中的摩擦力补偿。

本文首先分析单侧压力对密封圈摩擦力对称性的影响,使用改进的Stribeck模型对密封圈摩擦力进行建模;然后,基于提出的摩擦力模型构造带约束非线性最小二乘问题,使用信赖域法求解得到摩擦力模型的参数;最后,使用密封圈摩擦力测试台测量不受压和单侧受压工况下的密封圈摩擦力,并使用本文提出的摩擦力模型和辨识方法进行建模与辨识。

1 单侧受压密封圈摩擦力分析

1.1 单侧受压对密封圈摩擦力的影响

受气压负载的密封圈摩擦力情况较为复杂,根据行程不同,密封圈有4种不同的运动状态:第1种为完全静止;第2种为完全黏滑,此时密封圈只产生剪切变形,与试验阀杆杆壁之间没有宏观的相对滑动;第3种是部分滑动,此时密封圈的部分与试验阀杆杆壁之间产生宏观的相对滑动,但仍有部分区域处于黏结状态;第4种为密封圈相对杆壁产生完全滑动,此时摩擦力最显著的特征是不随着位移而改变。本文以第4种运动状态为重点,研究产生宏观位移时密封圈摩擦力随速度变化的关系。

在本文研究的工况下,密封圈受到单侧气动负载。根据实际测量结果,在相同速率下,密封圈在朝气动负载源头方向移动和远离气动负载源头方向时所受的摩擦力有显著的差别。这主要是由于密封圈受到单侧压力产生非对称变形,使得机构相反运动时密封圈与机构的接触状态不同,导致对应的摩擦力不同。针对此情形, Karaszkiewicz[19]提出了如图1所示的O型密封圈在外界压力下产生变形时等效接触力的理论计算模型。

图1 O型密封圈的理论分析模型

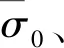
Δg=d-g

(1)

ε=Δg/d=(d-g)/d

(2)

s0=d(2ε+0.13)

(3)

(4)

σ0m=0.67E(2ε+0.13)

(5)

N0=π2E(D+d)•d(2ε+0.13)2/6

(6)

[1-exp(-4.6p/E)]+(2ε+0.13)

(7)

(8)

(9)

根据上述理论计算分析可知,在单侧气动负载作用下,密封圈向低压侧产生变形,使得其与阀杆杆壁接触区域的形状、面积和等效接触力发生变化。使用Stribeck摩擦模型对接触点间的摩擦力建模,通过对接触区域积分可以得到密封圈与阀杆之间的总摩擦力。经过仿真分析可得,单侧受压密封圈在单个方向运动时,摩擦力与运动速度之间的关系可以由Stribeck模型很好地近似,但朝相反方向运动时Stribeck模型的参数存在显著差异。因此,使用具有对称性的Stribeck模型无法准确描述单侧受压密封圈的摩擦力与运动速度之间的关系,需要研究单侧受压密封圈摩擦力的建模与辨识。

1.2 经典摩擦力模型问题分析

当前,摩擦力模型已多达数十种[20-22],这些模型从不同角度反映了摩擦力的最大静摩擦特性、库伦摩擦特性、粘性摩擦特性、Stribeck效应、预滑动特性、摩擦滞后特性、可变静摩擦效应和摩擦记忆等静、动态特性[23]。

Stribeck摩擦模型是使用最为广泛的静态摩擦模型。LuGre模型等动态摩擦模型相比于静态摩擦模型可以更全面地描述摩擦现象,包括摩擦滞后、可变静摩擦效应、预滑移位移阶段的摩擦效应。同时,连续性良好,可以更平滑地在不同摩擦状态间过渡。但其引入了包含不可测量状态变量的动态参数,使得摩擦模型参数辨识变得十分复杂。因此,静摩擦模型在工程实践应用中仍然经常使用。此外,动态摩擦模型相较于静态摩擦模型的精度提升有限。文献[24]发现Tustin静摩擦模型和动摩擦模型对于位置控制系统中摩擦引起极限环的预测效果近乎一样;文献[25]表明一个好的静态摩擦模型能够以90%的精确度近似拟合真实摩擦。

Stribeck模型是经典的静态摩擦模型之一,低速段摩擦力随速度增大而减小,高速段随速度增大体现出粘性摩擦特性。摩擦力与速度的关系如图2所示。

图2 Stribeck摩擦力曲线

Stribeck模型为

Ff=(Fc+(Fs-Fc)e-(v/vs)2+σ|v|δ)sgn(v)

(10)

Ff为非线性摩擦力;v为接触表面之间的速度;Fc为库伦摩擦力;Fs为最大静摩擦力;vs为Stribeck速度;σ为粘性系数;δ为非线性粘性系数;sgn(·)为符号函数。

根据1.1节分析,单侧受压下密封圈摩擦力关于速度呈不对称性。结合实测数据进行分析,其不对称性体现在以下几个方面:两侧运动方向的最大静摩擦力有差异;一侧Stribeck效应较明显,另一侧不明显;两侧粘滞摩擦现象不同,一侧斜率较大,另一侧斜率较小。

由于Stribeck模型是关于速度对称的,无法准确完整描述上述密封圈摩擦力的不对称性。但单独对一个运动方向的摩擦力进行分析,Stribeck模型可以实现较好的拟合。因此,可以选择Stribeck模型为密封圈摩擦力建模与辨识的基础,并加以改进。

2 密封圈摩擦力辨识方法

2.1 改进的非对称Stribeck摩擦模型

为了全面、精确地描述单侧受压密封圈摩擦力关于速度的不对称性,需要对Stribeck模型进行改进。工业实践中非对称摩擦现象很普遍,文献[26]发现了柴油机可变气门系统摩擦力的非对称性,并将LuGre模型改进为关于速度的分段函数以描述摩擦力的不对称现象;文献[27]采用改进的非对称LuGre模型以解决低负载电液系统的自适应摩擦补偿方案。对于情况相近的单侧受压密封圈,可采用类似的方法进行建模。

Stribeck模型可较好地描述朝某一侧方向运动时的密封圈摩擦力,可将原Stribeck模型修正为关于速度非对称的Stribeck模型,其表达式为分段函数,即

(11)

Fc1、Fs1、vs1、σ1、δ1与Fc2、Fs2、vs2、σ2、δ2分别表示速度为正、负时对应的摩擦模型参数,速度为正代表阀杆朝远离气源方向运动。

由于摩擦力模型(11)使用2套独立的参数分别描述正、负运动速度下的摩擦力,所以能够完整地描述密封圈摩擦力的不对称现象。

2.2 摩擦力参数辨识

2.2.1 带约束非线性最小二乘的摩擦力辨识模型

摩擦力参数辨识可视为一种优化问题,通过算法得出1组参数,使辨识模型输出的摩擦力Ff尽可能与实测数据吻合,即在解空间搜索1组最佳参数x=[Fc1,Fs1,vs1,σ1,δ1,Fc2,Fs2,vs2,σ2,δ2],使摩擦力理论模型与实测摩擦力之间的误差最小。故目标函数可以设计为两者的平方和为最小,即最小二乘拟合。由于待辨识的模型参数为库伦摩擦力、最大静摩擦力和粘性系数等正值物理量,故设定的约束是辨识参数均为正值。因此,密封圈摩擦力辨识模型为

(12)

N为密封圈摩擦力测量数据总个数;vi为第i次测量时的阀杆速度;Fi为第i次测量时的密封圈摩擦力实测值。

2.2.2 基于信赖域法的摩擦力参数求解

由于待优化的目标函数为非线性方程,需采用非线性最小二乘法进行求解。非线性最小二乘法主要包括搜索算法和迭代算法。本文采用信赖域法,属于迭代算法。这类方法实现简单、精度高及适应性强。

信赖域法主要分为以下4步。

a.设定待辨识参数初值x0和初始优化半径μ。

b.对于第k次迭代,在高斯牛顿法的基础上加上信赖区域,求解

(13)

J为Ff(x)的雅可比矩阵;D为系数矩阵;λ为拉格朗日乘子。

c.判定信赖区域近似的好坏程度,即

(14)

若ρ>3/4,则令μ=2μ,返回至步骤b;若ρ<1/4,则令μ=0.5μ,返回至步骤b;若ρ大于设定的阈值,则令xk+1=xk+Δxk。

d.若Δxk小于设定阈值,则结束流程,否则返回至步骤b。

参数辨识整体流程如图3所示。

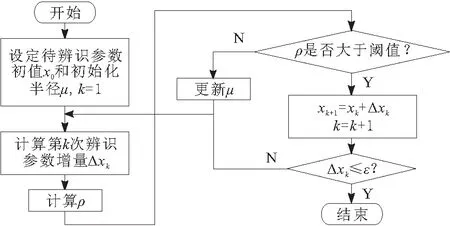
图3 基于信赖域法的非线性最小二乘法辨识流程

3 试验验证

3.1 密封圈摩擦力测试台

为了测量单向受压密封圈的摩擦力,采用基于无摩擦气缸、直线气浮轴承及电动伺服缸的密封圈摩擦力测试台,其结构如图4所示。

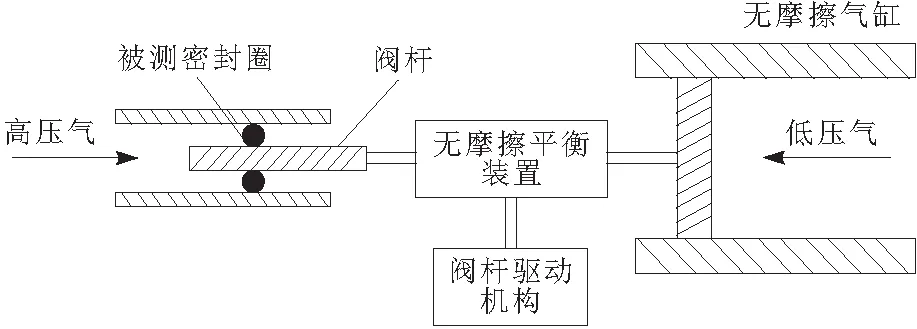
图4 密封圈摩擦力测试台

测试台主要由以下几部分组成。

a.气路系统:左侧高压气腔生成高压气作用于待测密封圈,模拟实际单侧受压工况。右侧低压气通过无摩擦气缸提供与高压气压力平衡的作用力。

b.无摩擦平衡装置:采用气浮导向机构,使用直线气浮轴承,在平衡左、右两侧高低气腔产生的作用力时,极大地降低了阀杆运动过程中其余环节产生的摩擦力,甚至达到无摩擦的效果,避免对密封圈摩擦力的测量带来干扰。

c.阀杆驱动机构:采用丝杠驱动方案,由有杆电缸、伺服电机和电机控制器等组成,可通过I/O控制实现配置速度、加速度和定位等功能。与无摩擦平衡装置相连,驱动阀杆左右移动。

d.测量系统:包括测量高低压腔压力的压力传感器、测量阀杆运动的位移传感器、测量阀杆驱动机构输出力的力传感器以及相应的控制系统等。

e.密封圈:测试台可选用不同材料、不同尺寸的密封圈进行测量,本文试验采用了丁腈橡胶密封圈,规格为8 mm×10 mm×1.8 mm,压缩率约为15%。

系统通过高压气罐产生高压气,模拟密封圈实际工况,使密封圈产生单侧受压的变形,并对阀杆产生向右的作用力。同时,另一侧的低压气供给低摩擦气缸驱动中间的无摩擦平衡装置,从而在阀杆上产生向左的作用力。通过调节左、右两腔的压力使得两侧的气压力近似相等,使装置处于近似平衡状态,此时装置的运行只受待测密封圈的摩擦力影响。再将阀杆驱动机构加载到无摩擦平衡装置,则可以带动阀杆克服密封圈摩擦力左右运动。

具体试验步骤如下:

a.设定高压气腔内的工作压力。

b.根据平衡方程,设定低压气腔内的平衡压力。

c.设定不同的运动速度,由阀杆驱动机构驱动,使机构保持匀速运动,测量高压腔压力p1、低压腔压力p2、阀杆驱动力F1,按照式(15)计算得出对应工作压力、运动速度时的密封圈摩擦力Ff。其中,A1、A2分别为高压腔、低压腔工作面积。

Ff=F1+(p1A1-p2A2)

(15)

d.根据上述步骤,建立特定工作压力下,密封圈摩擦力大小随运动速度变化的数据库。

3.2 单侧受压密封圈摩擦力辨识结果与分析

设定系统在无气压负载和单侧1 bar气压负载下进行试验,测量不同速度时的密封圈摩擦力,并采用Stribeck模型进行辨识,结果如图5所示。

图5 Stribeck模型辨识结果

由图5可以看到,在两侧无气压负载时,辨识模型拟合曲线能反映摩擦力大致变化趋势,但没有体现Stribeck效应,辨识值与真实值存在偏差。单侧1 bar气压负载时,辨识模型与试验值有-8～-5 N的偏差,误差较大。这也说明了Stribeck模型对密封圈摩擦力建模的不适用性。

用改进的非对称Stribeck模型进行辨识,结果如图6所示,辨识得到的模型参数如表1所示。

表1 密封圈摩擦力模型辨识参数

图6 密封圈摩擦力测量与辨识

改进的非对称Stribeck摩擦模型基本能描述密封圈在无气压负载和单侧受1 bar气压负载时的摩擦力变化情况。在低速段,密封圈摩擦力先达到一个较大值,随速度增大而逐渐减小,呈现一段下降趋势。超过某一临界点后,摩擦力又随速度增大而增大,呈正相关关系。

由于无法直接得到摩擦力模型参数的真值,为了判别识别模型精度,在此提出一种指标计算方法:首先沿纵坐标平移辨识后的模型,使其在零速度时的摩擦力为0;再用式(16)计算模型误差。

(16)

根据式(16)计算得到,无气压负载时模型误差为4.33%,单侧1 bar气压负载时误差为4.02%,模型精度较高。而用Stribeck模型建模时无气压负载时模型误差为13.80%,1 bar气压负载时误差为60.26%,模型精度低,完全不能使用。这也说明了用非对称Stribeck模型建模的合理性。

相同速度下,1 bar气压负载下的密封圈摩擦力要明显大于无气压负载情况。主要原因是施加气压负载时,密封圈与气缸壁和阀杆壁的接触面积与接触应力增大。

在1 bar气压负载下和相同运动速率时,阀杆朝远离气压源方向运动时的摩擦力显著大于朝气压源运动时摩擦力,呈现出关于速度的强不对称性。可能的原因是阀杆远离气压源运动时,密封圈的变形加剧,与阀杆的接触宽度和接触力明显增大,导致摩擦力增大。

4 结束语

为准确描述单侧受压密封圈的摩擦力,本文提出了改进的非对称Stribeck摩擦模型与带约束非线性最小二乘摩擦力辨识模型。使用密封圈摩擦力测试台分别测量两侧不受压与单侧受压2种工况下密封圈的摩擦力。结果表明:单侧受压会导致摩擦力关于速度呈现不对称特性;以远离高压侧的方向为正方向,则正方向的最大静摩擦力高于负方向的最大静摩擦力;负方向摩擦力以库仑摩擦和粘滞摩擦为主,无明显Stribeck现象。使用本文提出的模型与辨识方法完成了密封圈摩擦力辨识,验证了本文方法的有效性。