空间弱撞击对接机构精度分析与优化

汪 捷,王 峰,王鸿宇,张 锦,吴 红

(上海航天电子技术研究所,上海 201109)

0 引言

作为新一代的对接机构,不同于过去主要依靠传统机械阻尼缓冲的工作机理,空间弱撞击对接机构(low impact docking mechanism,LIDM)参考了周边式对接机构的经验,以机电一体化的设计思路,将对接过程分为柔性捕获阶段与刚性连接阶段,拥有独立的执行机构、控制系统以及配套的传动组件与动力系统[1]。

国内外众多学者设计并研究了不同对接机构在不同场景下的性能指标。张晓天等[2]针对一种模块化微小型卫星对接机构,分析了其运动学机构原理;沈涛等[3]计算了缓冲元器件的参数对于一种新型抱爪式对接机构捕获性能的影响;王文龙等[4]提出了一种新型的柔性杆式弱撞击对接机构;邹恒等[5]分析了一种航天器三指式对接机构运动学分析及尺寸优化;王勇等[6]提供了一种三爪式通用对接机构抓捕控制方法;刘洋等[7]设计了一种面向空间服务的新型变拓扑多面体对接机构;常娟等[8]设计了新型运载火箭捆绑对接机构,探讨了助推器与芯级对接距离与拉力的关系;侯文伟等[9]针对某新型GEO卫星与其他航天器的对接过程,设计了一种卫星对接装置;Salisbury等[10]提出了采用运动雅可比矩阵的条件数作为机器人的灵巧度用以衡量对接系统的精度判别;Yoshikawa[11]提出了一种可操作度的概念来衡量对接系统的灵巧性;黄剑斌等[12]阐述了一种弱撞击交会条件的对接补加一体化机构;韩伟等[13]研究了对接锥的型面设计方法;慕忠成等[14]创新移植电磁原理和“笔帽式”锁紧原理,提出了一种适用于立方体纳卫星的1U微型电磁对接技术;刘艳浩等[15]针对传统的6-UPS型空间对接装置进行了运动学分析;王文龙等[16]阐述了一种低功耗、小质量、小包络尺寸的柔性杆式弱撞击自动对接机构。

现阶段众多学者针对不同的对接环境提出了各类新型的对接机构,而对于新型的弱撞击对接机构,南航聂宏团队具体研究了相关技术:陈传志等[17-18]建立弱撞击对接机构全刚体目标系统下的多体动力学模型,将力雅可比矩阵分解为2个分别与力和力矩传递相关的子矩阵,并计算出力和力矩传递性能的分布规律;徐敏等[19-20]分析了机构构型单一参数对于空间弱撞击对接机构的对接精度影响。但是对于弱撞击对接机构构型参数的多元优化设计资料较少,大多采用了过往经验或案例来进行误差精度分析。在对接过程中,对接精度研究成果对于机构构型的最优设计、对接机构传递运动与力的认知、控制算法等研究至关重要。

本文描述了在捕获阶段中弱撞击式对接机构(LIDM)的多约束精度优化问题,建立了弱撞击对接机构的运动学模型,推导了运动学正反解过程与误差模型。研究了在不同工况下工作空间对于LSR对接环的对接精度影响特征,并依据误差模型建立性能评价指标,利用改进后的遗传算法计算出在相应工作空间中LIDM的最优构型参数。最后利用数值仿真建模验证了最优构型参数的正确性和合理性。研究内容为对接机构的精度结构设计、误差的标定补偿工作提供了数据支撑,具有一定的工程应用价值。

1 运动学模型

空间弱撞击对接机构结构上拥有机电一体化的机构特点,如图1所示。捕获阶段中6根驱动臂通过控制相应的工作行程完成对接环LSR的位姿变换。相比以往常见的刚性对接机构,弱撞击对接机构借用这种特殊的六自由度机构,搭配上相应控制算法,可以实现低碰撞力与力矩。

图1 弱撞击对接机构

1.1 坐标系建立

LIDM拥有1个六自由度动平台,即对接环,通过控制6根执行推杆的伸出量来完成期望的对接环位姿。现将LIDM在空间中的尺寸抽象成结构,如图2所示。机构的固定平台与动平台分别分布有6个虎克铰,相应上、下铰链连接有执行推杆。每根执行推杆包含有1个移动副。现以固定平台的中心点O建立基坐标系O-XYZ,Z轴垂直固定平台的基准平面指向LSR,X轴与Y轴在固定平台基准平面,构成右手坐标系。以LSR环心O1为中心,建立随体坐标系O1-X1Y1Z1,Z1轴平行LSR纵向对称轴朝外,与X1轴和Y1轴构成右手坐标系。记O-XYZ的6个铰链点为A1～A6,O1-X1Y1Z1的6个铰链点为a1～a6。这12个铰链点在各坐标系中是固定的。现为研究方便,令A1～A6处于半径为R0的外接圆上,a1～a6处于半径为r0的外接圆上,相邻较近的一对铰链点与中心的夹角记为θ,且沿中心对称分布。对接环上铰接点在随体坐标系中坐标记为ai,固定底环上铰接点在基坐标系中坐标记为Ai。

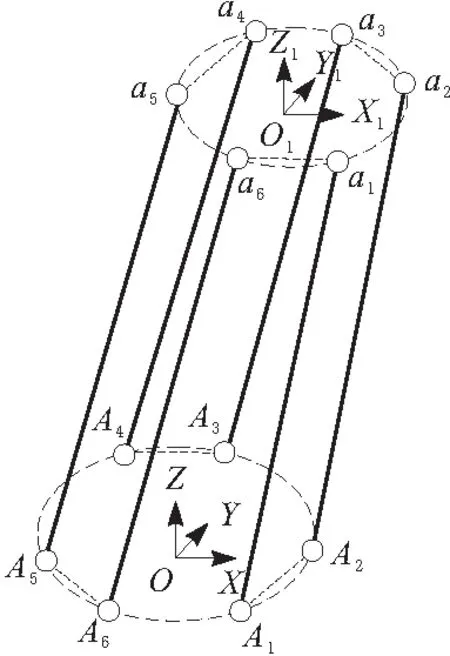
图2 弱撞击对接机构结构

1.2 运动学反解

6根执行推杆的长度为操作空间,O1-X1Y1Z1相对于O-XYZ的位姿为相应的映射空间。运动学反解过程中采用RPY角的描述形式,即已知对接环的位姿[xyzαβγ]T,求出该状态下执行推杆的长度。

由位置关系可知O1在O-XYZ的坐标表示为

(1)

由姿态角关系可知O1-X1Y1Z1相对于O-XYZ的旋转变化矩阵,即

(2)

执行推杆的长度可以由相应的Aiai两铰接点距离决定。利用旋转变化矩阵将ai转换到O-XYZ。根据几何关系易得第i根推杆上下铰接点的距离为

ldi=|li|=|P+R×ai-Ai|

(3)

i=1,2,…,6

由式(3)可由对接环位姿得到相应的执行推杆上铰接点在O-XYZ的坐标,其模长即为执行推杆长度。

1.3 运动学正解

运动学正解问题将已知机构的6个杆长li(i=1,2,…,6)输入,求解末端运动平台的姿态变量。考虑到运动学正解中,解析解的求解难度较大,这里采用数值解法,即利用多元牛顿迭代法处理联立的六元非线性方程组。

正解过程等价于求解式(4),即

(4)

利用数值解法解决正解问题的具体过程为:

(5)

(6)

(7)

进而得到迭代一次的值为

X1=X0+δ

(8)

反复迭代至最终值趋于稳定,规定最终迭代次数j满足|δ|./Xj<ε时,认为精度达到要求,正解问题得到解决。

LIDM运动学模型的建立为结构优化提供了基础。

2 LIDM捕获系统精度分析

2.1 速度雅可比矩阵

运动传递性能利用速度雅可比矩阵描述,如果该雅可比矩阵的行列式为0,意味着该系统运动不确定,而处于病态矩阵的状态下,求解精度会大大下降[21],即很小的驱动臂行程误差会引发巨大的姿态误差,故在结构设计上必须避免弱撞击对接机构呈现特殊的形位。

速度雅可比矩阵为

(9)

驱动臂沿杆速率可看成上铰链速度沿杆的速度分量,即

vi=ui·[ω×(Rai)+v]

(10)

ui为第i根驱动臂的沿杆单位向量。

对式(10)化简并处理为矩阵形式,即

(11)

可得雅可比矩阵的表达式,速度雅可比矩阵主要考虑了执行推杆行程误差带来的精度影响。而仅仅考虑执行推杆带来的误差是不够准确的,2.2节将综合考量误差来源与产生的精度影响。

2.2 误差模型建立

弱撞击对接机构在捕获阶段的对接精度主要与对接环LSR的位姿精度决定,包含有位置误差和姿态误差。误差的来源主要来自2个方面:执行推杆的长度误差和各铰接点的定位误差。

对式(3)中的向量表达式取微分可得

δldi·ui+ldi·δui=δp+δR·ai+R·δai-δAi

(12)

δp为LSR的位置误差,是由LSR质心位置p引起的定位误差;δR为对接环的姿态函数,即

(13)

处理为矩阵形式可得:

(14)

事实上,Jp正是弱撞击对接机构的速度雅可比矩阵。当Jp为非奇异矩阵时,系统存在对接环LSR精度为

(15)

根据式(15),对于某一确定构型LIDM的捕获对接阶段,只要获知执行推杆的杆长误差与各铰链的定位误差,即可求得当下对接环的位姿误差。

3 LIDM捕获系统结构优化设计

合适的初始对接位置可以有效提高弱撞击对接机构的对接精度,但LIDM的结构参数对于对接精度的影响会更大。综上可知,对接环的位姿误差取决于执行推杆的杆长误差、各铰链的定位误差、工作空间以及系统结构参数。LIDM作为机电一体化的对接机构代表,结构参数对于LIDM的运动、力学性能传递影响极大,且结构参数本身具有高度的相关性。现以LIDM的对接精度为主要优化目标,探求LIDM的最优结构参数。

3.1 优化设计变量

弱撞击对接机构为机构优化设计的设计变量,主要由几何构型参数与位姿参数决定。选取优化的几何构型参数为

X=[rRαβH]

r、R分别为上、下虎克铰所对应的LSR外接圆、基座外接圆半径;α、β分别为LSR对接环与基座的结构角;H为初始状态下的LSR距基座的平衡距离。

3.2 优化设计变量的线性约束

考虑到弱撞击对接机构的技术要求和工作空间限制,需要先给出几何构型参数X的线性约束,即

(16)

同时,几何构型参数X还受到工作空间限制,主要包括驱动臂总长的限制、转动副转角的限制和结构框尺寸限制。

3.3 优化设计变量的非线性约束

弱撞击对接机构在捕获过程中,上下铰链对应位置之间的距离决定了驱动臂的总长,但驱动臂有最大与最小距离限制,即

(17)

P和R为LSR相对于基座的位置矢量和旋转矩阵;ai和Ai为第i根驱动臂的上、下铰链点于动、基坐标系下的坐标。则存在长度限制为

lmin≤ldi≤lmax

(18)

弱撞击对接机构的上下铰链在设计上类似虎克铰链,存在2个自由度,对接环LSR、底座与各驱动臂之间通过转动副连接,该转动副的限制角可以由沿相应驱动臂轴向的单位向量ni与相应所属固连坐标系的沿Z轴的单位向量na和nA的夹角计算得出,具体表达式为

(19)

θamax、θAmax与转动副、驱动臂自身结构特点有关。

结构框安装于基座上,结构上起到支撑与保护的作用,在捕获工作初期,对接环收拢在结构框内部,准备对接时依靠6根驱动臂的工作行程来伸出,这要求6根驱动臂在工作行程期间不可与结构框产生干涉现象。根据结构设计,最容易发生干涉的位置出现在结构框的最大高度h处,受限于结构框内径r。

第i根驱动臂所在直线的空间直线参数方程为

(20)

令z=h,可得

(21)

为满足结构框的结构限制,驱动臂在伸缩过程中不可与结构框发生干涉,需要满足

x2+y2

(22)

3.4 性能评价函数

为提高LIDM的对接精度,综合评判工作空间中对某一结构构型参数下的位姿精度[22]。以6种工况下偏差期望加权求和的倒数作为性能评价指标,其值越大则误差越小,代表该构型参数越优秀。

(23)

3.5 改进遗传算法

遗传算法是一种常见的用于机械结构优化的算法,本质上是一个具有定向制导的随机搜索技术。遗传算法的循环过程包括选择、交叉和变异,在生成初始种群后,依据适应度函数对种群中每个个体进行评估,在接下来的循环过程中不断淘汰劣等个体(适应度较低),保留高适应度个体,在一定的循环次数后得到最终种群,由此得到优化的一个或多个可行解。

鉴于算法研究对象是一个复杂的非线性多目标优化过程[23],标准遗传算法经多次试验并不能很好地收敛全局最优解,对标准遗传算法进行改进,增设局部搜优算子与全局寻优算子,并增加精英保留策略保留当代最优的子种群。

局部搜优算子以当代适应度较高的个体子群二进制编码为基础,对于其有效位的后半段进行基本位变异,加强算法局部搜优能力。全局寻优算子改进了原有的变异算子,则当算法整体达到收敛时,对种群有针对性地施加一定程度的变异来打破可能存在的局部最优欺骗。程序整体框架流程如图3所示。

图3 改进遗传算法流程

4 算例及结果分析

弱撞击对接机构的对接初始条件和技术要求如表1所示。表1数据参考了以往国内外的成功经验以及现有的对接机构的设计参数等,结合任务需求给出。为了模拟LIDM的工作环境,工作行程的设定参考表1的数据。

表1 LIDM技术要求

按照设计要求,设计基座环结构角β=20°,对接环结构角α=20°,上虎克铰链对应铰点圆半径r=600 mm,下虎克铰链对应铰点圆半径R=800 mm。初始状态下的LSR距基座的平衡距离H=500 mm。执行推杆直线精度取0.05 mm,铰接点定位安装精度偏差不超过0.1 mm。LIDM在捕获对接过程中的工作空间范围参考表1,定义径向x、y方向上为-130～130 mm,轴向z方向参考原初始位置为-300～300 mm,姿态角偏差为5°。

改进遗传算法的最优解优化过程如图4～图6和表2所示。

表2 LIDM优化前后对比

图4 结构长度变化趋势

图5 结构角变化趋势

图6 位姿偏差期望之和变化趋势

图4～图6显示改进遗传算法程序共计算24代获得全局最优解,并展现了变量的优化过程。表2显示出最优解:顶、底环外接圆半径为698.7 mm和780.0 mm,顶、底环结构角为27.3°、35.3°,初始平衡距离为812.5 mm。在满足设计工作空间和多种约束条件的前提下,弱撞击对接机构拥有最高的对接精度,优化后的位姿偏差期望总和为0.054 7 mm,相比优化前的0.067 2 mm,误差降低18.6%。

改进遗传算法体现出多目标约束条件下优化设计的优越性和高效性,算法的改进具有通用性,可为机械设计等领域优化提供借鉴思路。通过误差模型建立相应的评价指标,并以LIDM的结构参数为优化变量,有效提高了LIDM的对接精度,研究结果为弱撞击对接机构的结构参数提供了数据支撑,具有一定的工程应用价值。

为验证基于误差模型与改进遗传算法优化得来的结构参数,选取Z轴工况以及结构优化得来的构型参数,以运动学正反解为模型基础,基于MATLAB建立数值仿真验证模型,用以求解在捕获对接的调姿过程中,质心位姿偏差的变化过程。

其中,执行推杆直线精度为0.05 mm,铰接点定位安装精度偏差不超过0.1 mm。

图7给出了LSR位姿偏差的变化趋势,其中,x、y、z表示LSR质心位置姿态偏差,α、β分别表示LSR质心的翻滚、俯仰、航偏姿态偏差。从图7中可以看出,LSR的6个方向上的位姿偏差,在数值上最大值在0.03附近,满足表1中的弱撞击对接机构的精度要求,验证了误差模型与改进遗传算法的正确性与合理性。

图7 LSR位姿偏差变化趋势

5 结束语

本文结合弱撞击对接机构的构型特点,建立推导了运动学模型,给出了运动学正反解的具体方法。为提高弱撞击对接机构的对接精度,推导建立了系统的误差模型,并研究了工作空间中不同工况下精度的变化趋势,得到了位姿精度的变化特征。结合误差模型,设计了一种改进的遗传算法对弱撞击对接机构的构型参数进行优化,进一步提高了系统的对接精度。基于运动学模型,利用数值仿真给出了纵向方向下弱撞击对接机构的精度变化,验证了改进后的LIDM构型参数满足设计要求。