基于可操作性指标的球型腕优化*

王 新，张永顺

(大连理工大学精密与特种加工教育部重点实验室，辽宁大连116024)



基于可操作性指标的球型腕优化*

王 新，张永顺

(大连理工大学精密与特种加工教育部重点实验室，辽宁大连116024)

可操作性是机器人结构设计时，需要考虑的一项重要性能指标。在研制的三自由度高集成球型腕的基础上，提出一种基于球型腕全域可操作性的均值和标准差的优化方法。该方法能够得到偏置斜面的最优角度，对机器人优化设计具有重要借鉴意义。

高集成度球型腕 可操作性指标 优化设计

机器人是一个将关节运动转换成末端执行器空间运动的机械系统，其可操作性描述了机器人对力和运动的全局转换能力。机器人雅克比矩阵是末端执行器速度与关节速度之间的映射关系，同时也反映末端受力与关节力矩之间的关系。因此，基于雅克比矩阵的可操作性不仅可以评估其灵活性，也能作为其结构参数优化的依据。本文通过可操作性对球型腕结构进行优化，这种方法对机器人优化设计具有重要借鉴意义。

机械手腕是连接末端执行器与机器人前臂的核心部件，承担着改变执行器姿态的任务。手腕的集成度和灵活性直接决定机器人的工作性能。本文在研究一种高集成球型手腕基础上，提出一种基于全域可操作性的均值和标准差的优化方法，并建立球型腕的偏置斜面角度的优化问题，这种方法对机器人优化设计具有重要借鉴意义。

1 球型腕结构及运动学分析

1.1 机械结构

三自由度高集成球型手腕的机械结构如图1所示，它由动力系统、传动系统和执行系统三部分组成。动力系统是由三个Maxon公司生产的RE26-118775型直流电机构成；传动系统由行星减速器、齿轮减速器和内外双十字万向节构成，内部万向节中心与空腔球体的中心重合，用于驱动球型腕的上半球，外部万向节中心也与空腔球体的中心重合，用于驱动悬浮输出端；执行系统由下半球、上半球和悬浮输出端构成，上下半球通过偏置斜面构成空腔球体，斜面倾斜角为φ，悬浮输出端通过轴承连接到上半球的输出轴。

图1 球型手腕三维模型

球型腕内外双万向节的轴线交点、上下双半球回转轴线交点都与球型腕球体中心重合，悬浮输出端轴线延长线过球体中心。因此，从结构上使得球型腕三个姿态的运动解耦，球型腕结构更加紧凑、运动灵活。

1.2 运动学分析

对球型腕进行运动学分析，通过D-H法建立坐标系如图2所示：坐标系Σ0为建立在球心的基坐标系，坐标系Σ1通过球心并与下半球固结，坐标系Σ2通过球心与上下半球偏置斜面固结，坐标系Σ3通过球心与上半球固结，坐标系Σ4与腕部输出端固结，S为末端输出轴参考点。

图2 球型腕运动坐标系

采用RPY角[10]描述球型腕的姿态，选取末端输出轴的S为参考点，由球型腕的正运动学得到经度角为α、纬度角为β、自转角为η。

(1)

球型手腕的雅克比矩阵表示手腕工作空间速度与关节空间速度的映射，即：

(2)

式中，σ的表达式为：

2 球型腕可操作性指标

球型腕是将关节速度和关节力矩转换为末端执行器速度和力的机械装置，可操作性指标是衡量球型腕系统对速度和力的转换能力，任意姿态下球型腕可操作性为：

(3)

当Kω越大时，认为球型腕的灵活性越好，在任意方向运动和施加力的能力越强，当Kω= 0时，球型腕处在奇异点上。球型腕运动过程中，雅克比矩阵J会改变，可操作性只能描述球型腕的某一个姿态的性能。

针对全操作空间内的可操作性，一般是以其平均值评估，即：

(4)

式中，W为球型腕整个工作空间。

球型腕的平均可操作性并不能反映性能的稳定性和波动大小，因此，本文采用标准差评估可操作性的波动程度：

(5)

球型腕的全域可操作性的均值和标准差不仅与姿态有关，而且与上半球和下半球的偏置斜面角度有关。考虑到万向节传动角度的限制，本文选择倾斜角φ的范围为[8°，22°]，球型腕的倾斜角φ为8°、12°、16°和20°时的可操作性指标如图3所示。

图3 球型腕可操作性

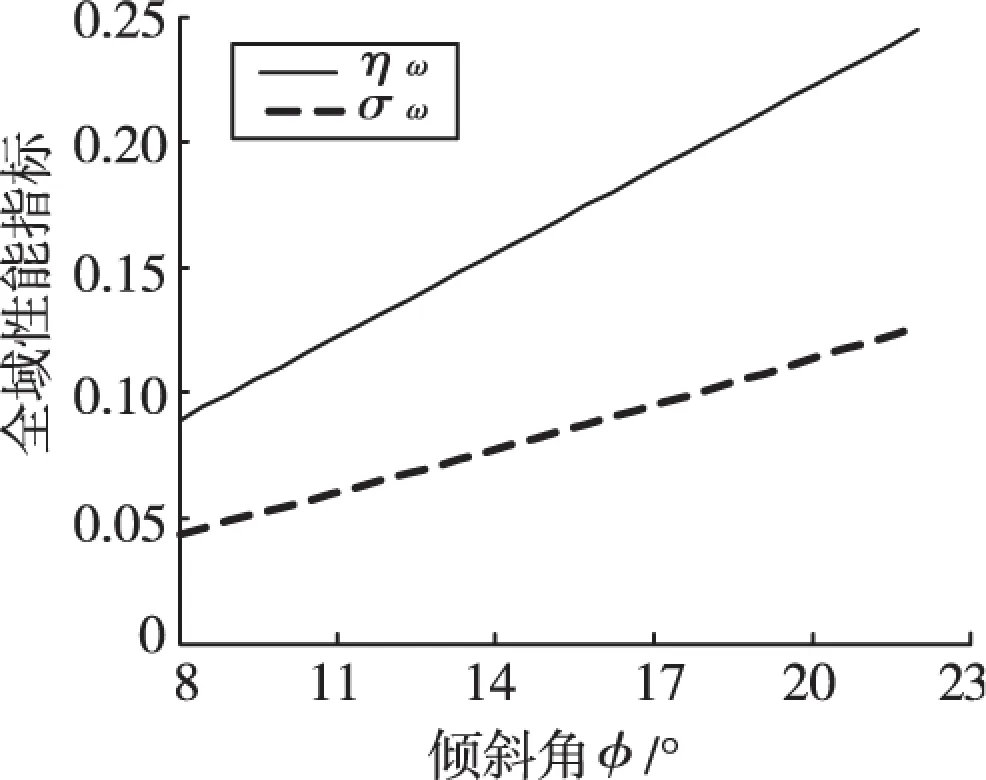
图4 球型腕全域可操作性能指标

球型腕全域可操作性的均值和标准差与倾斜角φ有关，其关系如图4所示。

由图3和图4可知，球型腕的全域可操作性ηω、σω与偏置斜面倾角φ呈线性关系。倾斜角越大，球型腕的可操作性越好，手腕越灵活，但可操作性波动程度也会增大。

3 球型腕结构优化

球型腕是连接机器人末端执行器与前臂的关键部件，既要求全域性均值较大，又要求波动程度尽量小。本文综合考虑球型腕可操作性均值和标准差，建立两目标函数：

(6)

将式(6)采用线性加权和法处理，即：

(7)

式中，λ1、λ2为权系数，且λ1+λ2=1，λ1>0，λ2>0。

(8)

根据α-方法，权系数λ1、λ2的表达式分别为：

(9)

由式(7)可得，权系数分别为λ1=0.347 6、λ2=0.652 4，即评价函数为：

F=0.347 6ηω-0.652 4σω

(10)

图5 评价函数随倾斜角变化曲线

评价函数F与倾斜角φ的关系如图5所示。由图5可知，Fmax=3.723 1×10-3，对应的全域可操作性能指标ηω=0.174 7，σω=0.087 4，此时斜面倾角φ=15.724 1°。在实际球型腕结构设计时，通常将斜面倾角取整为φ=16°。

4 结论

在机器人结构设计时，通过可操作性建立优化函数，是为了满足机器人较大可操作性和较小可操作性的波动程度。本文基于全域可操作性的均值和标准差构造球型腕偏置斜面角度的优化目标函数，得到偏置斜面的最优角度，球型腕具有良好的可操作性， 且可操作性的波动程度较小。该方法从结构上保证了机器人具有良好的性能，对机器人优化设计具有重要借鉴意义。

[1] 刘迎春, 余跃庆, 姜春福. 机器人可操作性研究进展[J]. 机械设计与研究, 2003, 19(4):34-37.

[2] Huang C，Xie C，Zhang T.Determination of optimal measurement configurations for robot calibration based on a hybrid optimal method[C]// International Conference on Information and Automation, 2008,12(4):281-285.

[3] Salisbury J K, Craig J J. Articulated hands force control and kinematic issues[J]. International Journal of Robotics Research, 1982, 1(1): 4-17.

[4] Gosselin C M, Angeles J. A global performance index for the kinematic optimization of robotic manipulators[J]. Journal of Mechanical Design, 1991, 113(3): 220-226.

[5] Klein C A, Blaho B E. Dexterity measures for the design and control of kinematically redundant manipulators[J]. International Journal of Robotics Research, 1987, 6(2):72-83.

[6] Liegeois B A. Automatic supervisory control of the configuration and behavior of multibody mechanisms[J]. Systems Man and Cybernetics IEEE transactions on, 1977, 7(12): 868-871.

[7] Kokkinis T, Paden B. Kinetostatic performance limits of cooperating robot manipulators using force-velocity polytopes[C]// Proceedings of the ASME Winter Annual Meeting. 1989: 151-155.

[8] 陈安军, 马学文. 双臂机器人机构力方向可操作性研究[J]. 机械设计与制造, 2005(1):107-109.

[9] 陈安军, 许佩霞, 李国梁. 双臂机器人机构速度方向可操作性研究[J]. 南京理工大学学报(自然科学版), 2005, 29(2):202-205.

[10] 张彤晓, 程顺足, 见浪護,等. 基于形状变化的冗余机械手可操作性分析[J]. 机械工程学报, 2011, 47(19):38-48.

Optimization of spherical wrist based on maneuverability

WANG Xin，ZHANG Yongshun

Maneuverability is an important performance index to be considered in the design of robot structure. An optimization method based on the mean value and standard deviation of global maneuverability of the spherical wrist is proposed, on the basis of the newly development of 3-DOF highly integrated spherical wrist structure. The optimal angle of the offset slope is obtained by using the optimization method, which demonstrates that the proposed method is of great implications in designing robot structure.

highly integrated spherical wrist，maneuverability index，optimization design

TP242.2

A

1002-6886(2016)06-0001-04

国家自然科学基金资助项目(61175102，51277018)。

王新(1990-)，男，硕士研究生，主要研究方向：机器人控制。

2016-05-15