基于混沌理论和CNN-OSVM的水轮机空化状态识别方法
2023-11-21李显伟邹淑云王文豪周泽华
刘 忠, 李显伟, 邹淑云, 王文豪, 周泽华
(长沙理工大学 能源与动力工程学院, 长沙 410114)
空化是影响水轮机安全稳定运行的主要因素之一,对其进行准确有效的状态识别已成为水力机械研究领域关注的重点和难点[1]。声发射(Acoustic emission,AE)作为一种无损检测方法,可用于采集水轮机空化状态下产生的频率范围为20~1×103kHz的AE信号[2]。
空化发生的不同阶段,其AE信号具有不同的特征,因此可以通过挖掘不同空化状态下的AE信号隐藏特征进行空化的状态识别。在水力机械研究领域,一系列状态识别模型被相继提出。Azizi等[3]利用经验模态分解方法处理空化振动信号,将得到的模态分量作为特征参数,通过蜜蜂算法结合交叉验证算法优化广义神经网络分类器,有效提高了空化状态分类准确率。Shervani-Tabar等[4]通过经验模态分解方法提取离心泵振动信号特征,再输入到支持向量机(Support vector machine,SVM)完成空化状态识别。Bordoloi等[5]建立了基于优化算法的SVM离心泵空化振动信号诊断模型,使用网格搜索算法对SVM参数进行全局寻优,提高模型精度。因水力机械空化故障机理复杂、工况多变,导致空化振动信号和AE信号具有强烈的非线性和非平稳性[6]。传统的时频分解方法虽然可以分解AE信号且提取到一部分信号特征,但由于AE信号非线性较强,仅通过时频分解方法容易遗漏故障特征关键信息,造成特征提取不够完整,使得信号特征结合机器学习模型的识别准确率不高。
近年来,深度学习在机械故障识别领域得到了广泛应用。作为经典的深度学习模型,卷积神经网络(Convolution neural network,CNN)能够在减少模型训练参数量的同时避免发生过拟合现象而备受青睐[7]。Zhang等[8]将原始时间序列直接输入到CNN模型中进行训练,避免了人工特征提取的影响,证实该模型在克服噪声影响的同时可以提升识别精度。魏晓良等[9]提出了一种基于长短时记忆网络结合卷积神经网络(LSTM-CNN)的高速柱塞泵空化故障识别方法,实现了对不同进口压力下振动信号的空化等级识别。以上研究证实,将一维数据直接输入到CNN模型有助于解决信号特征提取不完整导致模型准确率低的问题。实际上,由于CNN模型局部连接、权值共享、池化的结构特性,其更适合处理二维图像数据,在基于图像处理的识别诊断方面取得了较好的效果。张安安等[10]将一维轴承振动信号转化为二维时域波形图(以下简称时域图)作为输入数据集,通过CNN模型完成故障识别。李恒等[11]对轴承振动信号进行短时傅里叶变换得到频谱图样本,将其输入到CNN模型中得到较高的识别精度,并通过增加故障种类提升模型的鲁棒性。
将信号时域图、频谱图直接输入CNN模型进行故障分类识别,能够最大化CNN模型的结构优势。但对于非线性较强的信号,不同类型故障的时域、频域信号的故障信息区分度较低,导致CNN故障识别模型准确率和泛化能力提升不高。刘忠等[12]利用最大Lyapunov指数证实水轮机空化AE信号具有混沌性。兰朝凤等[13]采用混沌相空间重构技术,将相图、Poincaré截面图等混沌特性图像分析方法应用到水轮机压力脉动信号特性研究上。可见,采用混沌理论的相空间重构技术将空化AE信号还原至混沌空间,完整复原混沌空间中的非线性动力学特征,可以解决时域图数据集、频谱图数据集故障特征信息区分度较低的问题。因水轮机空化AE信号的非线性程度较高,传统的CNN模型会引入过多训练参数,容易产生过拟合和减弱模型泛化能力的问题。而采用基于结构风险最小化原则、泛化能力强、计算速度快[14]的SVM代替传统CNN模型的Softmax可以弥补这一不足。
因此,笔者将经过网格搜索算法结合K折交叉验证算法全局寻优的SVM分类器(OSVM)代替传统CNN模型的Softmax分类器,建立CNN-OSVM模型。以混沌相空间重构相图代替水轮机空化AE信号时域图、频谱图作为模型输入数据集,以提升模型识别精度和泛化能力,为水力机械空化状态识别提供一种新的方法和思路。
1 理论基础
1.1 相空间重构
利用相空间重构可以将含有重要信息系统分量的混沌吸引子从高维空间中还原出来。对离散时间信号z(i)重构相空间,其中i=1,2,…,N。
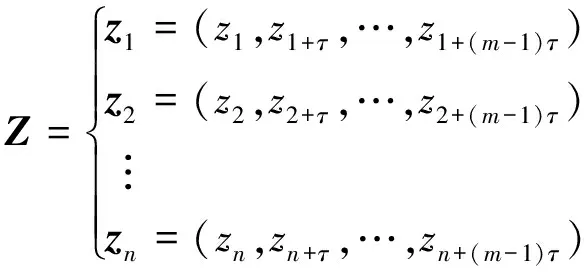
(1)
式中:Z为重构之后的相空间;τ为延迟时间;m为嵌入维数;n=N-(m-1)τ。
在相空间重构中,延迟时间τ及嵌入维数m的选择非常关键。分别采用互信息法和虚假最近邻点法来确定最佳延迟时间τ0和最佳嵌入维数m0[15]。
获得相图的步骤如下:
(1) 确定相空间重构的参数τ0和m0。
(2) 对非线性信号按式(1)进行相空间重构,将该信号重构为m0维相空间。
(3) 在相空间内选取任意分量及其相邻分量,即可得到二维相图。
1.2 卷积神经网络
CNN是一种具有卷积运算和深度结构特性的前馈神经网络。常见的CNN模型结构如图1所示。输入层可以执行多维数据的处理,将输入的数据进行归一化;输出层则要根据模型的实际使用情况和模型的具体构造来确定;隐含层包括卷积层、池化层和全连接层[16]。
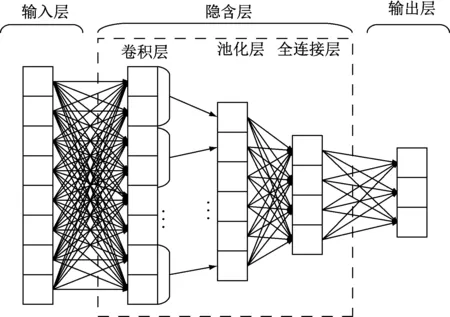
图1 CNN结构Fig.1 Structure of CNN
(1) 卷积层
卷积是一种特殊的积分变换方法。在卷积运算的基础上,利用线性滤波器对输入的图像数据集进行特征提取。在卷积层中,每个卷积核都可以进行特征提取。通过式(2)的卷积运算,对所有图像进行特征提取。在卷积运算之后,将线性、不可分割的多维特性映射到多维线性可分性的空间,输出新的特征图。
(2)
式中:h为卷积层数;j为卷积核个数;i为特征图数目;a(h,j)为第h层第j个特征图;a(h-1,i)为h-1个卷积层输出的特征图;k为卷积核;b为偏置项;x(·)为激活函数,激活函数为ReLu函数[7]。
(2) 池化层
经过卷积层完成特征提取步骤后,其输出会被输入到池化层。池化层能够提高特征图像的主要特性,同时还能压缩特征图像,降低模型训练的参数。最大池化和平均池化是2种常见的方式。
(3) 全连接层
在输入图像经卷积和池化多次迭代之后,全连接层将各局部特征非线性地整合为全局特征,从而求出最终各类别输出。
1.3 优化支持向量机
SVM在结构风险最小化原则和VC维理论的基础上,利用核函数对样本进行映射,从低维到高维构造出最佳分类超平面,其分类性能优于 CNN的 Softmax分类器[17]。SVM的数学表达式为:

(3)
式中:ω为最优平面法向量;ρ为惩罚因子;ζi为松弛因子;P为样本特征集合中特征的数量;mi为第i个样本的类别;li为第i个输入样本特征向量;d为分类阈值;z为样本集合。
通过非线性径向基核函数构造决策函数f(l):
(4)
惩罚因子ρ和参数γ的选取决定SVM能否达到全局最优。采用网格搜索算法结合K折交叉验证算法[18]对这2个参数进行全局寻优,步骤如下:
(1) 设置网格搜索算法搜索步长及范围,生成网络,任意相交节点就是一组(ρ,γ)。
(2) 采用K折交叉验证方法,将训练集随机分为K(K≥2)个数目大致相等、不相交子集,然后将第2个子集到第K个子集作为训练集进行训练,第1个子集作为测试样本,得到第1个模型分类准确率,重复训练K次可得K个模型测试集下的分类准确率,再对这些准确率取平均,作为分类器的性能指标。
(3) 将每一节点采用K折交叉验证进行评估,平均准确率最高时,将该节点作为SVM的全局最优参数。
2 基于混沌理论和CNN-OSVM的水轮机空化状态识别方法
针对水轮机空化状态识别准确度不高的问题,建立基于混沌理论和CNN-OSVM的水轮机空化状态识别方法,如图2所示。
1.整合现有资源,推广六方合作模式。由种猪场提供父母代种猪和商品仔猪,饲料企业配送饲料,担保公司为种猪场和养猪户提供贷款担保,协会(专业合作社)负责产前、产中、产后服务,农户负责养猪,保险公司提供保险服务。
其主要步骤为:
(1) 将采集到的同一工况下水轮机空化AE信号按照不同的空化系数进行空化状态分类。

图2 基于混沌理论和CNN-OSVM的水轮机空化状态识别方法Fig.2 State recognition method of hydraulic turbine cavitation based on chaos theory and CNN-OSVM
(2) 确定不同空化状态AE信号的最佳延迟时间τ0和最佳嵌入维数m0,进行相空间重构,得到相图数据集。
(3) 将相图数据集根据空化状态设置类型标签,将其输入到CNN-OSVM模型。其中:
① 利用测试集数据实时验证CNN模型的准确率和损失值。在规定的迭代轮次内,若模型的准确率和损失值满足要求,则保存CNN模型的最优参数和权重;否则,对CNN模型初始参数进行调整。
② 将CNN模型中全连接层的输出数据作为OSVM的输入数据,通过网格搜索算法结合K折交叉验证算法对SVM参数进行全局寻优,完成空化状态识别。
3 试验分析
3.1 水轮机空化AE信号来源及预处理
笔者在闭式水力机械试验台上进行了混流式水轮机模型空化试验[19]。同一工况下根据空化系数将水轮机空化分为无空化、空化初生、空化发展和严重空化4种状态。
同一工况下4种不同空化状态下的AE信号时域图如图3所示。通过互信息法和虚假最近邻点法计算样本数据集的相空间重构参数τ0和m0,结果见表1。分别对4种不同空化状态的AE信号进行相空间重构,选取每个相空间内前2个相邻分量画出二维相图,如图4所示。
分别从采集到的4种空化状态数据中以2 048采样长度截取水轮机空化AE信号数据组成样本序列,并全部进行相空间重构,根据空化严重程度对数据划定标签,数据集分布及标签如表2所示。
3.2 模型参数
对CNN模型进行反复训练调试,确定模型参数见表3。将训练好的CNN模型和全连接层输出的数据输入到OSVM分类器进行全局寻优。设置网格搜索算法搜索范围[2-5,25],步长为0.5,每一节点采用K折交叉验证进行评估,设置K=10。平均准确率最高时,得到SVM最优参数。
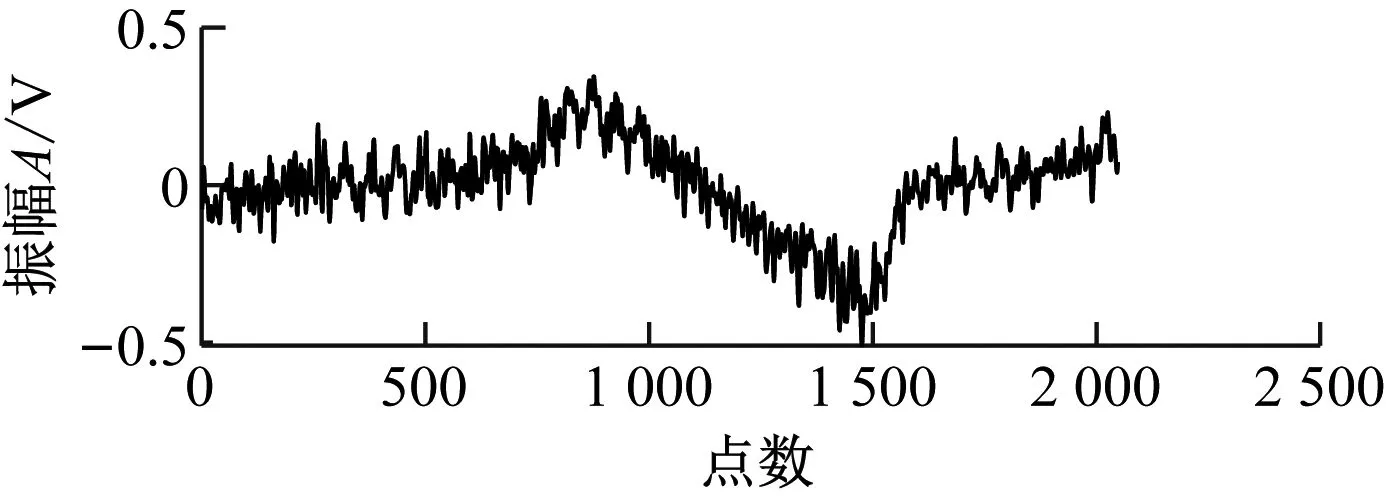
(a) 无空化

(b) 空化初生
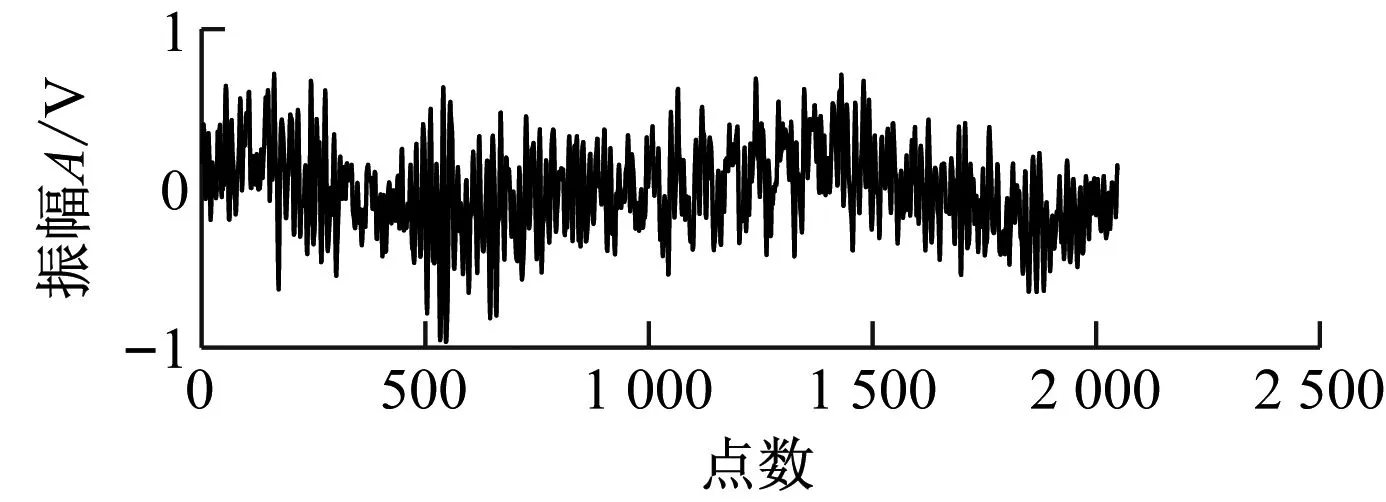
(c) 空化发展

(d) 严重空化图3 水轮机空化AE信号时域图Fig.3 Time domain waveform of hydraulic turbine cavitation AE signals

表1 不同空化状态AE信号相空间重构参数Tab.1 Phase space reconstruction parameters of AE signals under different cavitation conditions

(a) 无空化

(b) 初生空化

(c) 空化发展

(d) 严重空化图4 水轮机空化AE信号相图Fig.4 Phase diagram of hydraulic turbine cavitation AE signals
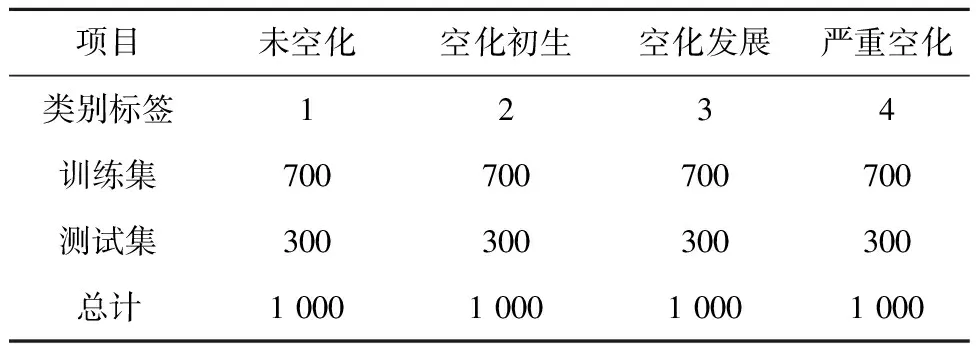
表2 数据集分布及标签Tab.2 Dataset distribution and labels

表3 CNN-OSVM模型参数
3.3 结果与分析
3.3.1 本文方法的测试结果
通过测试集验证,得到某一次模型测试的混淆矩阵如图5所示。图中坐标数字1~4为4个空化状态的类别标签(见表2),对角线数值代表每类状态的识别准确率。
由图5可知,CNN-OSVM模型对于无空化、严重空化的状态测试集识别准确率达到100%,对于空化初生和空化发展状态也有较高的识别准确率,测试总识别准确率达到98.8%。
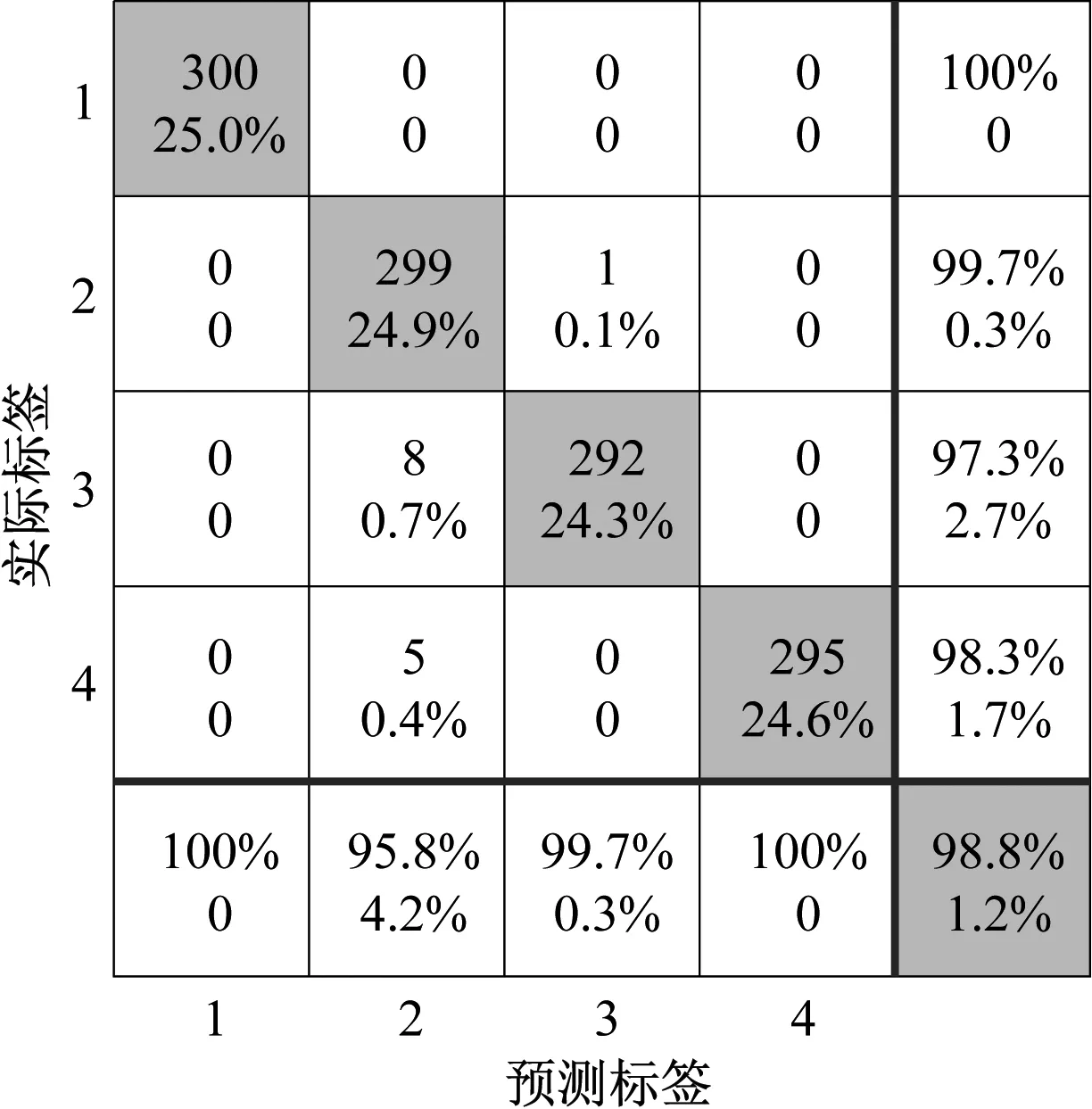
图5 混淆矩阵Fig.5 Confusion matrix
3.3.2 与其他图像数据集的对比
为验证CNN-OSVM模型结合混沌理论的效果,将表2的输入样本生成时域图样本数据集(见图3),经快速傅里叶变换生成频谱图样本数据集(见图6)。将2种图像数据集分别输入到CNN-OSVM模型中进行10次测试,每个空化状态的平均识别准确率如图7所示。由图7可知,时域图数据集模型测试平均识别准确率为78.1%,频谱图的平均识别准确率为92.4%,相图的平均识别准确率为98.8%。
不同类型图像数据集的CNN-OSVM模型识别准确率差异较大,原因是混沌相图相较于时域图、频谱图可以更好地表征空化AE信号的非线性特征。水轮机内部的空化是由过流部件真空压力逐渐降低引起的,在无空化状态下流体运动情况良好,通过AE信号反映出的混沌程度较轻,其时域图、频谱图、相图都与空化之后的信号有较明显的区别。因此,3种类型数据集对无空化状态的识别都有较高的识别准确率。随着真空压力逐渐升高,空化初生到空化发展,大量空泡阻塞部分流道,流体的连续性和稳定性受到破坏。在空化初生和空化发展阶段,AE信号时域图和频谱图特征信息区分度较低,CNN-OSVM模型识别二者AE信号时域图的识别准确率仅为62.8%和67.1%,CNN-OSVM模型识别空化初生、空化发展AE信号频谱图的准确率为86.6%和86.7%。而通过相空间重构处理,可以还原AE信号的动力学特征,放大空化初生和空化发展阶段AE信号的区别,CNN-OSVM模型识别空化初生和空化发展相图的准确率为98.0%和99.7%。严重空化阶段,大量的空泡随流体流动到高于压力临界值的区域发生溃灭,流体流态的紊乱程度剧增,混沌特性更强,空化AE信号特征频率更加凸显。因此,模型在严重空化时频谱图和相图数据测试准确率较高,而严重空化的时域图振幅与波形变化相对较小,模型识别AE信号时域图的准确率仅为84.1%。

(a) 无空化
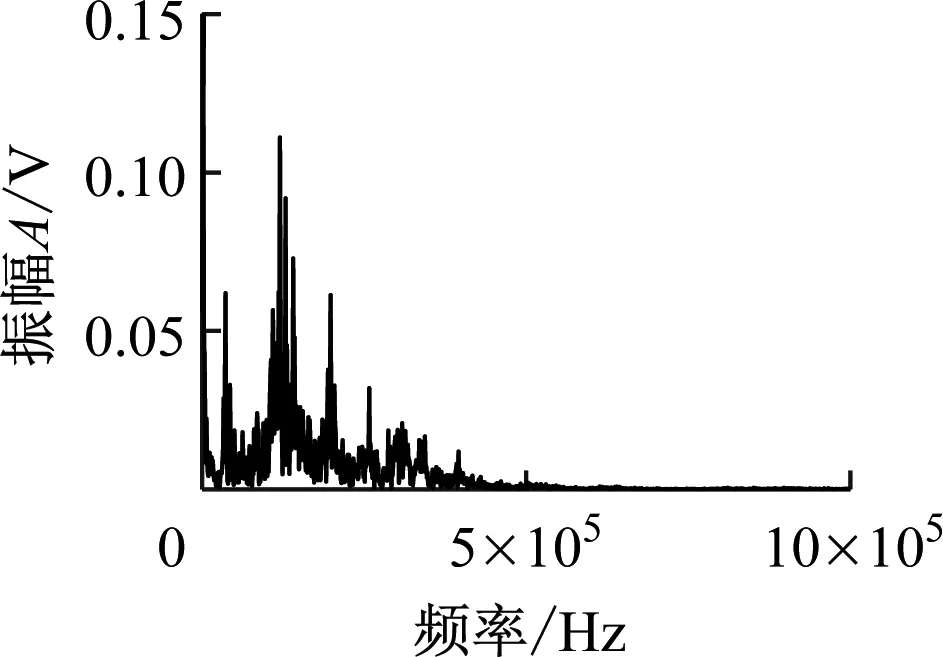
(b) 空化初生

(c) 空化发展
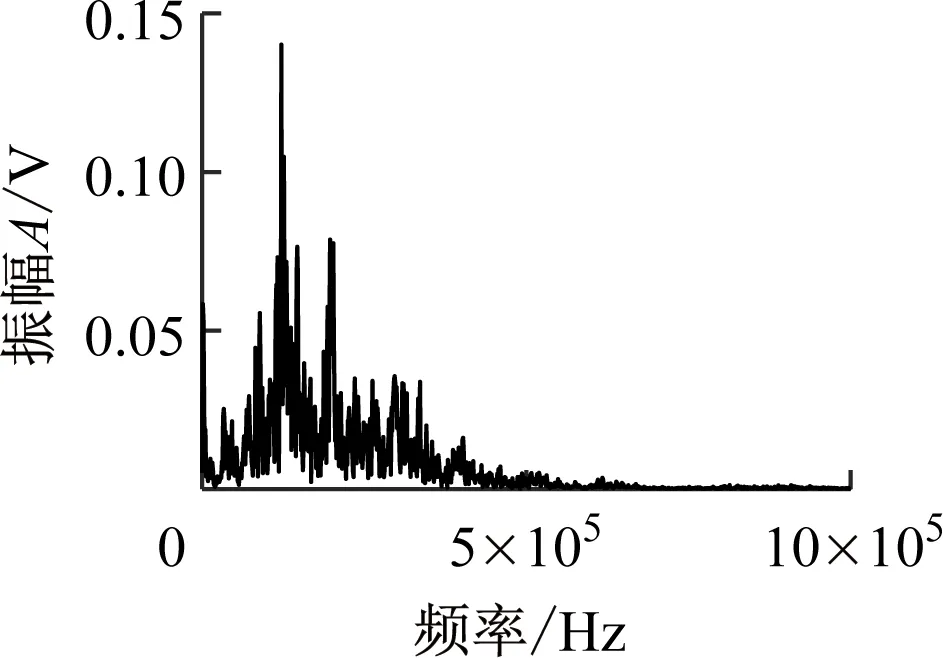
(d) 严重空化图6 水轮机空化AE信号频谱图Fig.6 Frequency spectrogram of hydraulic turbine cavitation AE signals

图7 不同数据集空化状态测试准确率Fig.7 Accuracy of cavitation sate in different datasets
通过CNN-OSVM模型识别4种空化状态准确率的对比分析,无空化、严重空化状态下识别准确率都较高,证明CNN-OSVM模型对3种数据集均有较好的识别能力,模型具有较高的泛化性。空化初生、空化发展状态相图数据集的识别准确率远高于时域图数据集和频谱图数据集,证明采用混沌理论相空间重构方法,还原AE信号的混沌动力学特征,可以大幅提升空化状态渐变的识别准确度。
3.3.3 与其他模型的对比
为验证CNN-OSVM模型的优势,将该模型与传统CNN模型以及OSVM模型进行对比分析。CNN模型与CNN-OSVM模型结构类似,采用Softmax分类器对全连接层提取的特征进行分类。将相图数据集通过方向梯度直方图进行特征提取,生成特征向量输入到OSVM模型。每个模型都采用相同的相图数据集进行训练测试,10次训练测试结果准确率如图8所示。
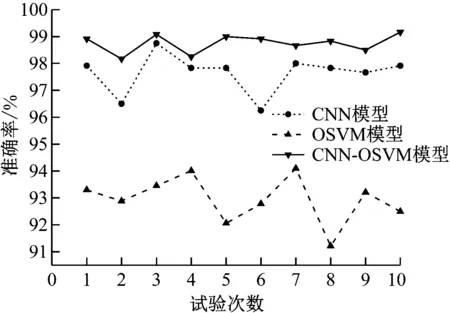
图8 不同模型准确率对比Fig.8 Accuracy of different models
对10次模型训练结果准确率求平均可得,CNN-OSVM模型测试集准确率为98.8%,CNN模型测试集准确率为97.7%,OSVM模型测试集准确率为92.9%。采用OSVM分类器来代替传统Softmax分类器,可以有效提升模型识别准确率,CNN-OSVM模型测试集准确率比CNN模型测试集准确率提高了1.1百分点,比OSVM模型测试集准确率提高了5.9百分点。证实CNN-OSVM模型能够更准确地对水轮机空化状态进行故障分类。
4 结 论
(1) 经混沌相空间重构处理的相图数据集CNN-OSVM模型识别准确率高于时域图数据集和频谱图数据集。
(2) CNN-OSVM模型、CNN模型、OSVM模型识别相图数据集测试平均准确率分别为98.8%、97.7%和92.9%,说明所建立的CNN-OSVM模型具有更高的识别准确度和泛化性,可用于水轮机空化状态识别。
