基于Kriging组合模型和NSGA-Ⅲ算法的转子裂纹参数识别
2023-11-21王晓东陈虹潮
胡 楷, 马 军,2, 王晓东,2, 陈虹潮
(1.昆明理工大学 信息工程与自动化学院,昆明 650500; 2.昆明理工大学 云南省人工智能重点实验室,昆明 650500)
转子作为旋转机械的核心部件,在机械、动力工程领域中起着重要的作用,一旦发生转子裂纹故障,轻则造成转子的断裂或系统的停机,重则引起经济损失及人员伤亡。因此,有效判断和识别裂纹故障,对保证转子系统的安全运行具有重大意义。
目前,国内外学者针对转子裂纹故障的识别研究开展了大量的工作,主要可以概括为裂纹检测和定量识别裂纹参数2个方面[1-2]。裂纹检测方面,刘杨等[3]基于裂纹柔度矩阵建立裂纹转子系统的动力学模型,从振动信号中提取出裂纹的故障信息。向玲等[4]基于全谱图分析了裂纹故障振动信号的变化规律和特点。焦博隆等[5]提出了一种基于蝙蝠算法优化参数的变分模态分解(VMD)诊断转子裂纹故障方法,通过频率结构特征识别出转子裂纹的故障特征。刘军等[6]基于振动能量空间分析方法研究了转子系统的振动特性,实现了转子裂纹故障的诊断。向玲等[7]提出了一种基于轴心轨迹形态的分析方法,为转子裂纹故障诊断提供了一种新方法。上述研究只能定性判断是否存在裂纹故障,难以识别发生裂纹故障的位置及故障,进而导致对转子系统结构健康的监测不足。
为了实现裂纹参数的识别,高海洋等[8]首次将Kriging代理模型技术应用到裂纹识别领域,有效识别了悬臂梁和板结构的裂纹参数。随后,有学者将Kriging技术用于转子裂纹参数的识别。Sinou等[9]提出了一种基于Kriging和多项式混沌展开(PCE)的建模方法,用于预测不同裂纹参数下转子系统临界转速和谐波分量。Lu等[10]将裂纹参数识别的逆问题转化为寻找最优裂纹参数的目标优化问题,通过不断更新样本建立代理模型,用于转子裂纹参数的量化识别。Wang等[11]提出了一种基于Kriging代理模型和非支配解排序遗传算法Ⅲ型(NSGA-III)算法的转子裂纹参数识别方法,对转子裂纹的位置、深度等进行识别。近年来,针对单个Kriging代理模型预测效果不理想的问题,部分学者对Kriging组合建模进行了研究,Yang[12]在考虑地质统计学及方格数据的基础上提出了一种Kriging组合模型,在地质领域的空间预测取得了比单个Kriging代理模型更准确的结果。Shi等[13]分析了机械结构的时变可靠性,提出了一种自适应Kriging组合模型,并通过实际算例验证了所提方法的精确性。然而,在Kriging组合模型的建立过程中,不同相关函数形式构建的Kriging代理模型的预测精度各不相同,进而引起Kriging组合模型的相关函数选择不确定性问题,导致后续的识别方案失败,从而严重影响Kriging组合建模技术在裂纹识别领域的应用。
针对上述存在的问题,笔者基于逐步回归模型筛选策略,提出了一种Kriging组合模型的建模方法,并将此模型用于建立转子系统的裂纹参数与动力学响应关系,避免原先复杂且耗时的有限元计算过程。基于Kriging组合模型构建多目标函数,通过NSGA-Ⅲ多目标优化算法进行裂纹参数的寻优,实现转子系统裂纹参数的定量识别。将Kriging组合模型与单个Kriging代理模型和指数函数-高斯函数的组合模型(ESK)进行对比分析,验证了所提方法的精确性。
1 裂纹转子系统的动力学模型
1.1 裂纹转子系统有限元建模
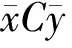
A1=R2[π-cos-1(1-μ)+(1-μ)γ]
(1)
(2)
(a) 旋转前
(b) 旋转后图1 裂纹转子横截面坐标系Fig.1 Cross section coordinate system of cracked rotor μ=h/R
式中:R为转子轴的半径。
裂纹开口部分在X轴和Y轴的截面惯性矩分别为IX,C和IY,C,其计算公式如下:
sin-1(1-μ)]
(3)
(4)
裂纹单元横截面面积A1在X轴和Y轴上对应的惯性矩为I1和I2,计算公式如下:
I1=I-IX,C
(5)
I2=I-IY,C
(6)
式中:I为无裂纹转子的惯性矩。
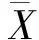
(7)
f1(t)=cosn(Ωt/2)=
(8)
(9)
式中:n、p为正偶数;j和i为求和过程中每次的取值;θ1为转子裂纹开始闭合的角度;θ2为转子裂纹完全闭合的角度;f1(t)和f2(t)为傅里叶级数余弦展开式。
假设转子裂纹位于第j单元,对于裂纹单元,新的刚度矩阵kce,j为:
kce,j=kj+k1,jf1(t)+k2,jf2(t)
(10)
式中:kj为裂纹单元全部关闭状态下的刚度矩阵;k1,j和k2,j为裂纹单元的刚度矩阵。
(11)
(12)
式中:E为弹性模量;l为裂纹单元的长度。
转子系统由转子、负载圆盘和滚动轴承组成,系统参数见表1。假定横向裂纹位于转子的某一单元,裂纹转子系统的有限元动力学模型如图2所示,模型离散为N个单元,每个单元有2个节点,每个节点仅考虑平移和转动方向的自由度,即具有4个自由度。根据转子动力学有限元法[15],考虑呼吸裂纹及陀螺效应的因素,裂纹转子系统的运动方程可表示为:
Mq″(t)+(C+ΩG)q′(t)+(K+K1f1(t)+
K2f2(t))q(t)=F+Fg
(13)
式中:K1和K2为4(N+1)×4(N+1)的矩阵,其中裂纹单元j对应的值由k1,j和k2,j代替,其他元素的值为0;M为质量矩阵[16];C为阻尼矩阵;G为陀螺矩阵;K为刚度矩阵;F为不平衡激励向量;Fg为重力矩阵;q(t)为4(N+1)×1的向量。
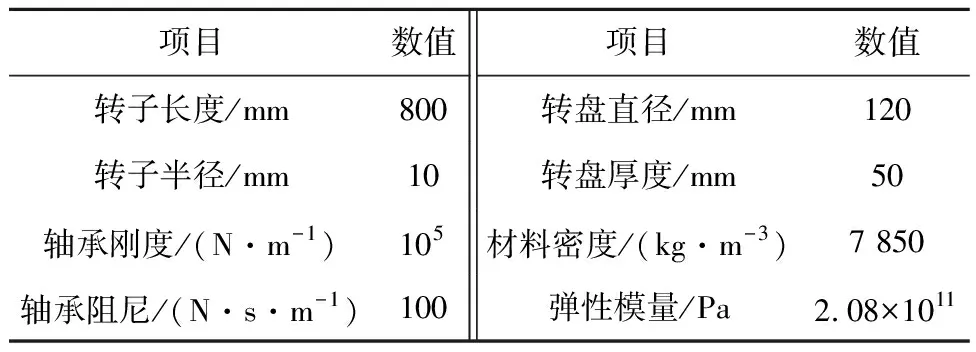
表1 转子系统参数
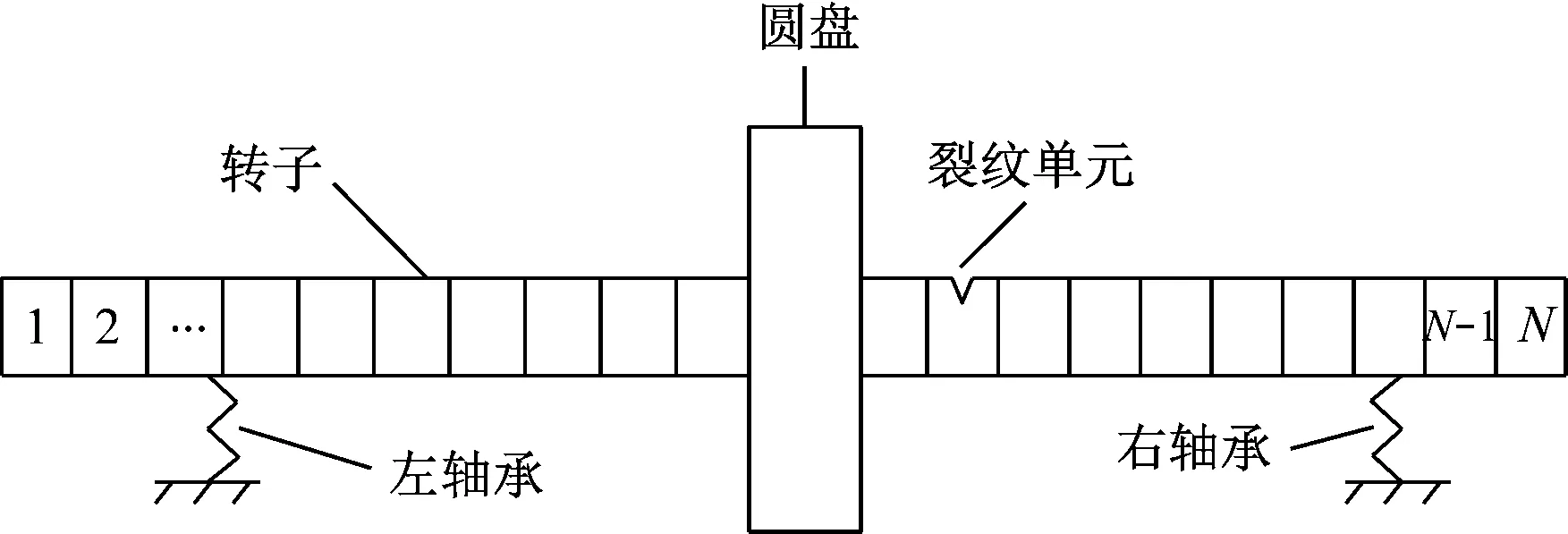
图2 转子系统有限元模型示意图Fig.2 Schematic diagram of finite element model of rotor system
1.2 振动特性分析及实验验证
为获取裂纹转子系统的振动响应,继而分析裂纹转子的动力学特性,采用Newmark-β法对式(13)进行数值积分求解,得到转子裂纹故障的振动加速度信号。运用FFT算法对信号进行处理,分析裂纹转子的频谱特征及其变化规律。根据实际实验条件,将裂纹转子系统划分为80个单元,转子裂纹位于50单元,左、右2个轴承位置分别在12和77单元。
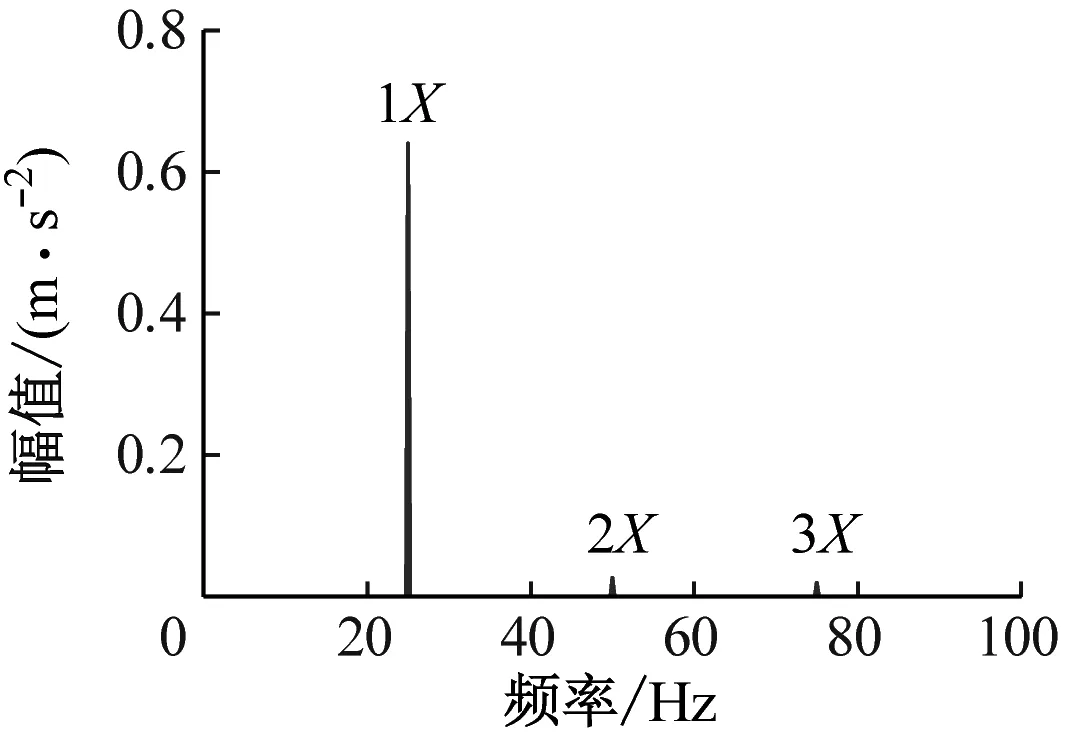
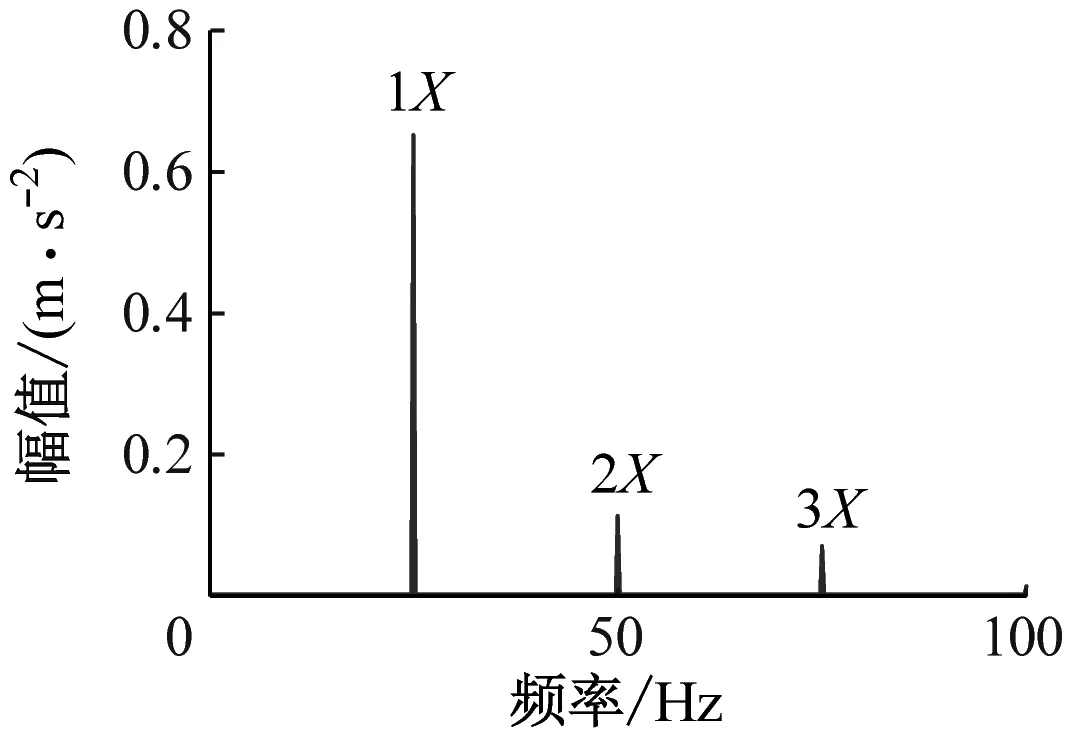
图3给出了转速为1 500 r/min、相对裂纹深度μ为0.2、0.4和0.6时的振动响应频谱图。由图3可知,频谱图中出现了转频为25 Hz、2倍频为50 Hz和3倍频为75 Hz的显著特征,在后续分析中分别简写为1X、2X和3X成分;当裂纹深度增加时,1X、2X和3X特征的幅值随之增加。
为验证动力学模型的正确性及分析结果的可靠性,对裂纹转子系统进行实验研究,图4为自主搭建的转子裂纹故障模拟实验平台,平台转子的直径为20 mm。实验采用JF2100加速度传感器进行测量,通过优泰动态信号采集控制测试系统uTekAcqu采集振动数据。实验配置了裂纹深度为2 mm、4 mm和6 mm的裂纹转子,分别对应于上述模型中的μ=0.2、μ=0.4和μ=0.6,裂纹转子细节如图5所示。该模拟裂纹由线切割机加工而成,以此实现对实际工业环境中转子裂纹故障的模拟,与动力学模型保持一致,设置系统的转速为1 500 r/min,通过测得的振动信号对其进行快速傅里叶变换(FFT),进而分析其动态特性。
(a) μ=0.2
(b) μ=0.4
(c) μ=0.6

图4 转子裂纹故障模拟实验台Fig.4 Rotor crack fault simulation test bench

图5 裂纹转子细节图Fig.5 Details of cracked rotor
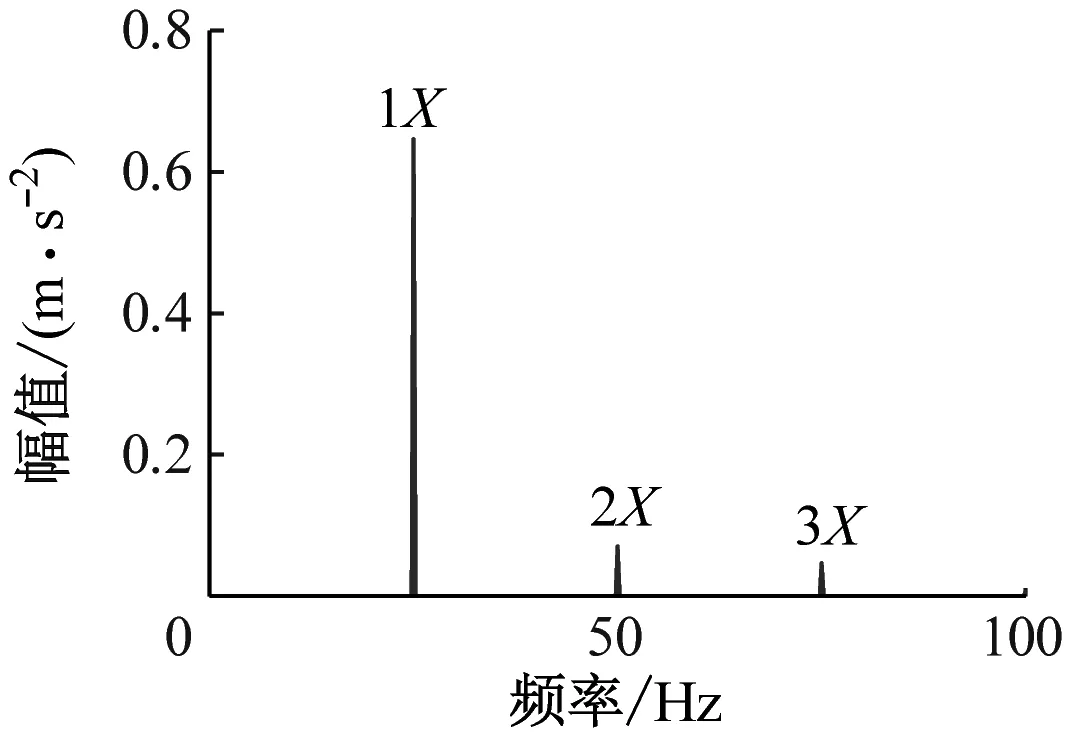
图6给出了转子裂纹深度为2 mm、4 mm和6 mm的频谱图。由图6可知,频域内出现明显的1X、2X和3X特征,且裂纹深度越大,所有特征对应的幅值越大。该实验结果对先前的数值仿真进行了部分验证,证明了所建动力学模型的正确性和预测故障特征的可靠性。
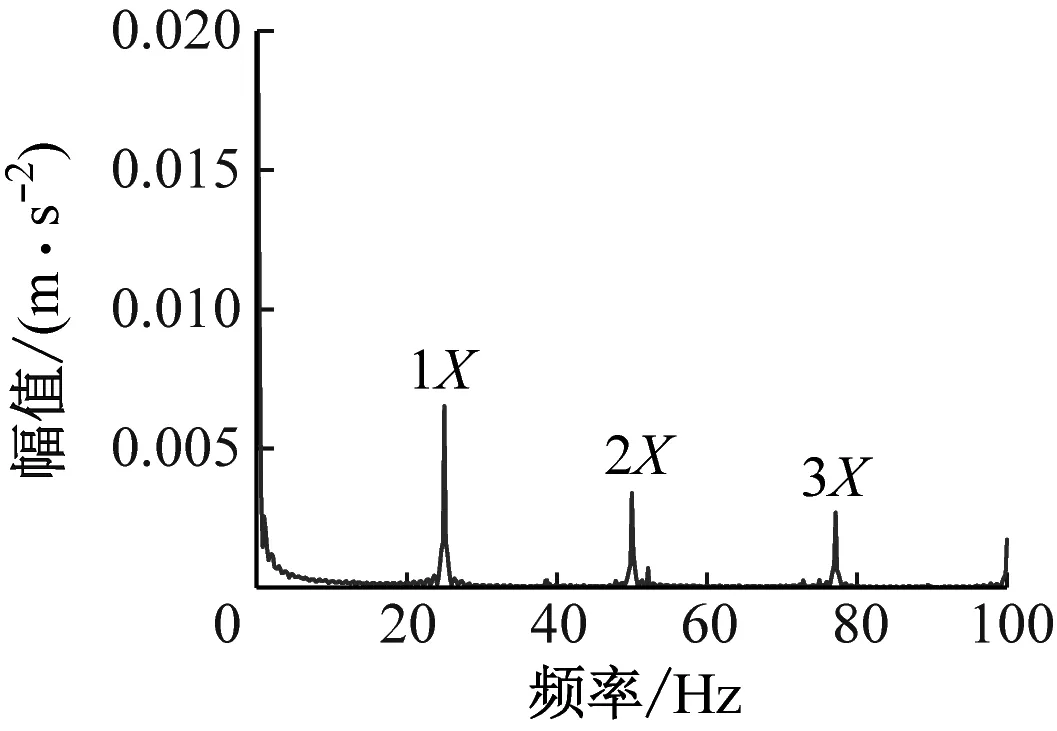
(a) 裂纹深度为2 mm
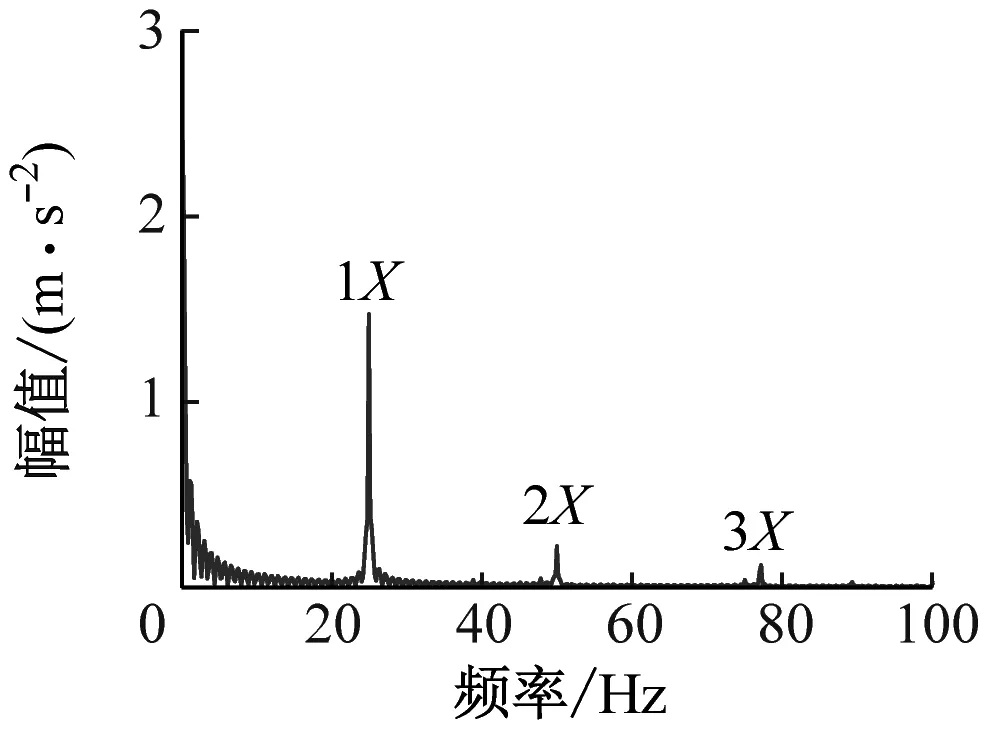
(b) 裂纹深度为4 mm
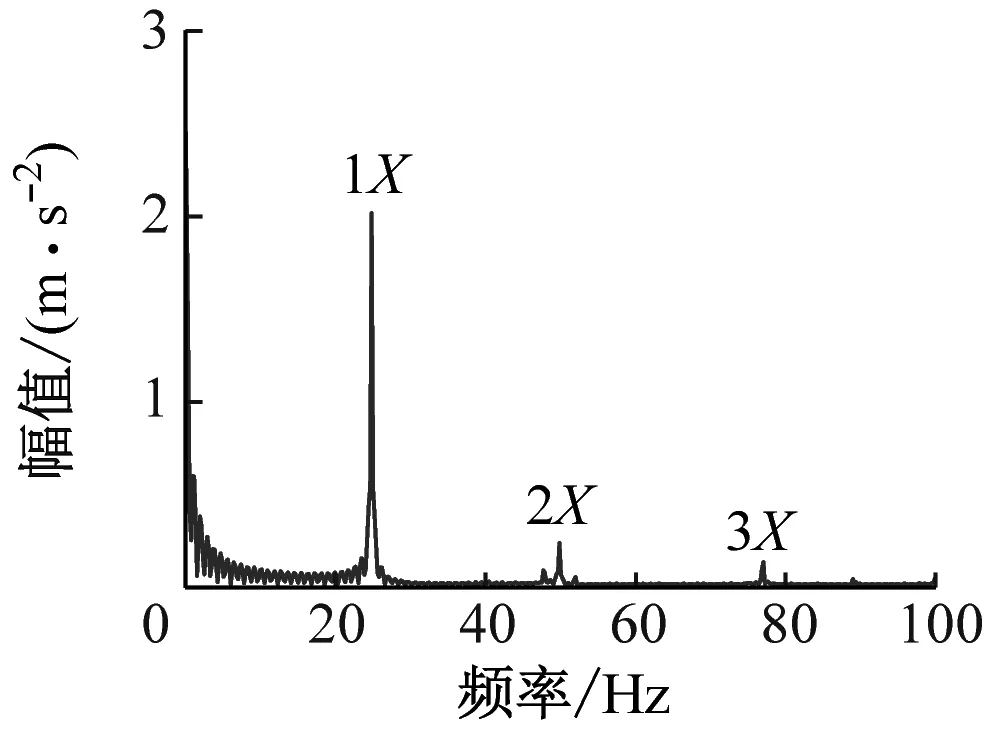
(c) 裂纹深度为6 mm
2 NSGA-Ⅲ和Kriging组合模型构建
转子系统裂纹参数定量识别的问题可以等效为多目标优化问题,因此考虑把实际裂纹参数和预测裂纹参数1X、2X和3X幅值的差异形成目标函数。为使目标函数达到最小值,需要通过多目标优化算法搜索出最合适的裂纹参数,从而实现裂纹参数识别的目的。在采用NSGA-Ⅲ算法进行多目标优化过程中,应用Kriging组合模型预测裂纹转子系统的1X、2X和3X幅值分布,避免复杂且耗时的有限元计算过程。
2.1 Kriging代理模型
Kriging代理模型是基于统计理论的插值近似模型,本质上是一种半参数化的插值技术。Kriging代理模型y(x)可表示为一个回归模型与高斯随机过程之和的形式[17],即
(14)
式中:F(β,x)为多项式回归函数;f(x)为关于输入参数x的基函数;β=(β1,…,βp)T为对应的权重系数向量;z(x)为系统的估计误差。
z(x)是协方差为Cov[z(xi),z(xj)]=σ2R(θ,xi,xj)、均值为0的随机分布,其中σ2为方差,R(θ,xi,xj)为超参数θ的相关函数,用于表征样本点xi与xj的空间相关关系,其数学表达为:
(15)
式中:m为预先设计变量的数目;dk为样本点k的欧氏距离;θk为超参数。
相关函数R(θ,xi,xj)有多种形式,Kriging代理模型中惯用的相关函数有指数函数、高斯函数、三次函数、球函数和样条函数。
2.2 基于逐步回归选择策略的Kriging组合模型
笔者所提出的新思路是在得到不同Kriging代理模型的基础上,引入逐步回归模型筛选策略,对获得的候选Kriging代理模型进行筛选,通过启发式权重系数法计算各筛选后模型的权重,形成新的组合模型。初始组合模型可表示为:
(16)
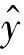
选择留一法交叉验证[18],分别建立基于指数函数、高斯函数、三次函数、球函数和样条函数的Kriging代理模型,所建模型依次表示为EXP、GAU、CUB、SPH和SPL,以此作为候选模型库。依据逐步回归法的思想[19],从候选模型库中选择显著性较好的模型加入到组合模型。对候选模型逐个检验,将不显著的Kriging代理模型进行剔除处理,模型选取规则为:当模型显著性P值小于0.05,则将其引入组合模型;当模型显著性P值大于0.05,则将其剔除。
基于逐步回归模型选择策略形成的最终Kriging组合模型可表示为:
(17)
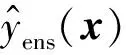
其中,利用启发式权重系数法计算wi[20],其计算表达式如下:
(18)
(19)
(20)
(21)
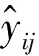
2.3 Kriging组合模型的构建过程
应用提出的Kriging组合模型建立裂纹参数与裂纹转子系统超谐成分之间的关系。由于不同的裂纹参数在某一位置的超谐成分幅值很接近,使用一个测点难以识别出裂纹参数,但如果测点过多则会造成信息的冗余,为尽量与工程实际保持一致,经过综合考虑,选取转子系统两轴承位置计算的振动响应来构建组合模型[11]。采用拉丁超立方抽样(LHS)抽取初始样本X,包括裂纹位置和相对裂纹深度,基于有限元动力学模型,计算裂纹转子系统的1X、2X和3X超谐成分幅值来构建矩阵Y,即
(22)
(23)
式中:xi=[liμi]为第i个裂纹参数样本;li为裂纹位置;μi为相对裂纹深度;An,mX(xi)为第n个测点的mX超谐成分幅值。
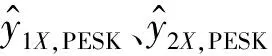
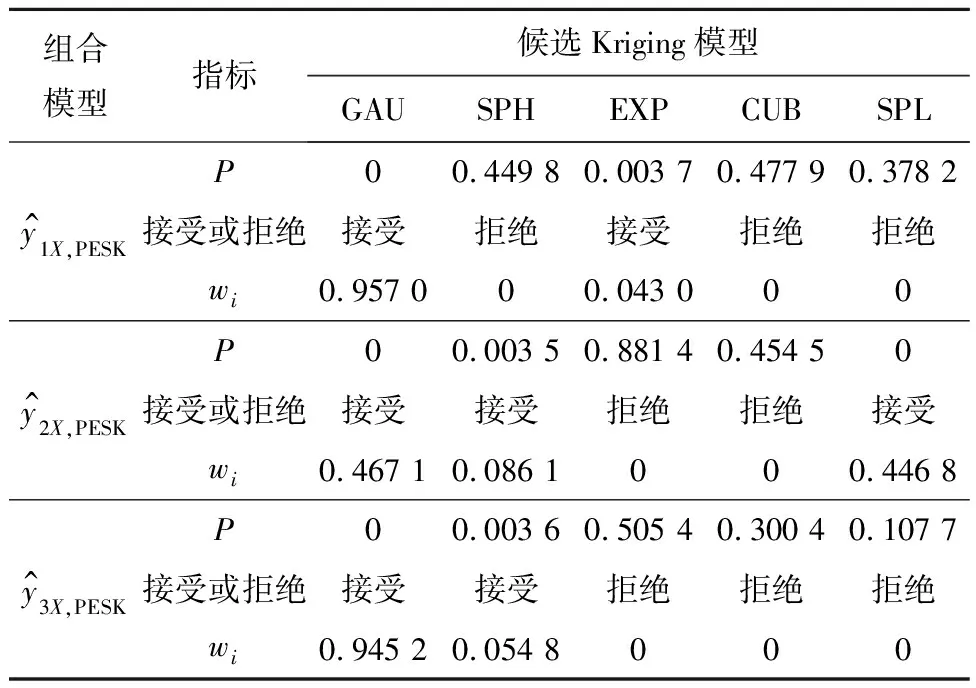
表2 代理模型的逐步回归优化筛选结果
在表2中,第1行中第1列P值小于0.05,表示基于GAU的Kriging代理模型被放入1X特征Kriging组合模型中。第1行中第2列P值大于0.05,表示基于SPH的Kriging代理模型拒绝放入1X特征的组合模型中。第3行表示已筛选出Kriging代理模型的权重系数。
2.4 多目标函数的构造及裂纹参数识别
多目标优化问题是多个目标函数在相关的约束条件下同时进行优化的问题,笔者将裂纹参数定量识别的问题等效为多目标优化问题,利用Kriging组合模型预测谐波特征幅值与实际谐波特征幅值的差异,构成多目标函数。因此,裂纹参数的识别问题可以转化为式(24)和式(25)的多目标优化问题。
findx*={l*,μ*}
(24)
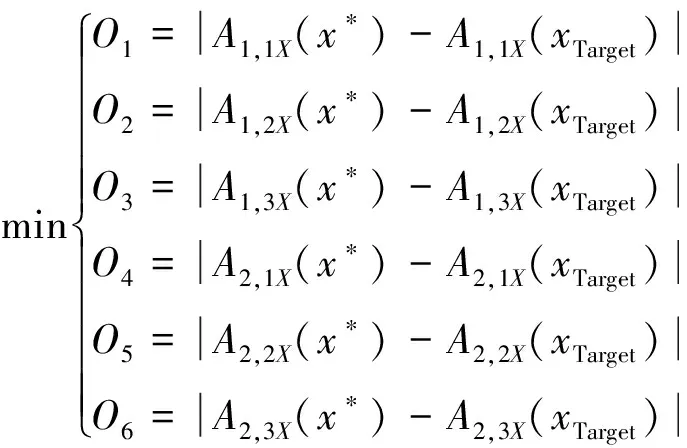
(25)
式中:x*为目标裂纹参数样本;l*为目标裂纹位置;μ*为目标相对裂纹深度;O1~O6为目标函数;An,mX(x*)为通过Kriging组合模型预测得到的超谐成分幅值;An,mX(xTarget)为在裂纹转子系统中测量、计算得到的超谐成分幅值。
考虑到实际环境中转子系统轴承两端附近不易出现裂纹故障[11],将约束条件设置为:
(26)
为解决上述多目标问题,使用NSGA-Ⅲ算法来进行迭代寻优,相较于传统的优化算法,其优势表现为当目标函数个数大于4时,NSGA-Ⅲ算法的优化效果更好[21]。基于Kriging组合模型和NSGA-Ⅲ的裂纹参数识别步骤如图7所示。通过NSGA-Ⅲ种群的交叉变异迭代最终获得一系列Pareto最优解,最后一个子代所有的参数可使全部目标函数达到最小,根据合适的评价指标在Pareto最优解中选择一组最佳裂纹参数作为最终识别结果。
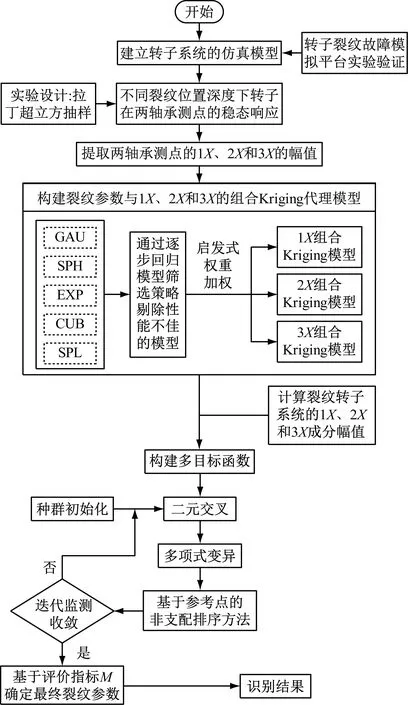
图7 基于组合代理模型和NSGA-III的裂纹参数识别流程图Fig.7 Flow chart of crack parameter identification based on combined model and NSGA-III
定义多目标权重M为裂纹参数最终选择指标,M是对最后一个子代的目标函数进行加权的总和,M的最小值所对应的个体为最终选择的裂纹参数,即
(27)
式中:ki为权重系数;O(i)为每个子代的目标函数值。
3 转子裂纹参数识别分析
3.1 裂纹参数定量识别分析
为了验证以上转子系统裂纹参数识别方法的有效性,基于以上Kriging组合模型和NSGA-Ⅲ多目标遗传算法,使用LHS生成训练样本,采用有限元动力学模型进行仿真实验,然后应用所提Kriging组合模型构建裂纹参数与1X、2X、3X幅值的关系,并利用NSGA-Ⅲ算法进行多目标优化。遗传算法的初始参数为:种群规模80,交叉概率0.5%,变异概率0.5%。
重新抽取5组裂纹参数作为验证样本,计算裂纹转子系统的1X、2X、3X幅值来进行识别方法的有效性分析。笔者详细分析第1组裂纹参数的识别过程,图8为6个目标函数优化过程中目标函数的均值随进化代数变化的结果,可以看出在进化代数大于18时所有目标函数值基本收敛。
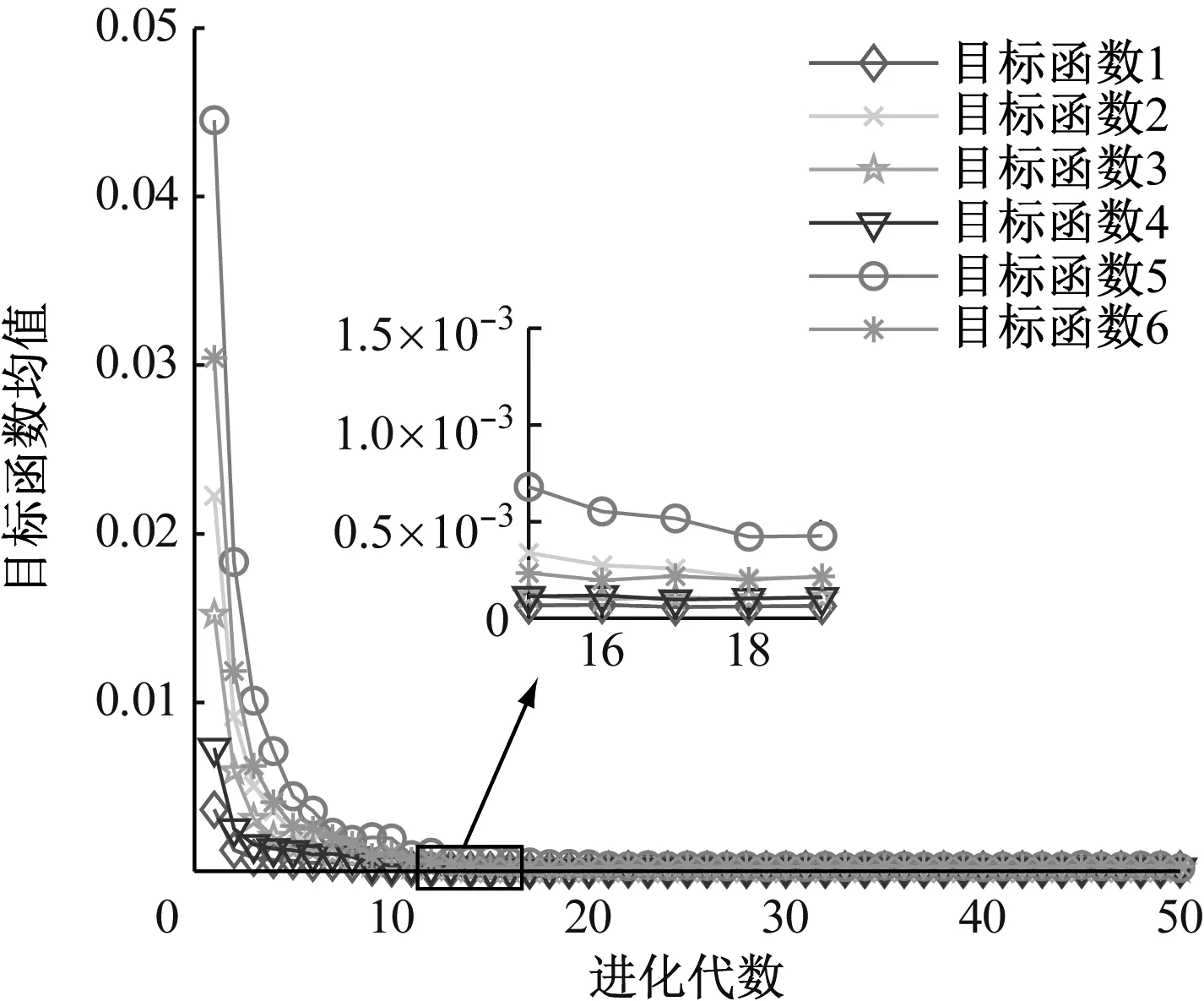
图8 目标函数的均值随进化代数的变化Fig.8 The changes of the mean value of the objective function with the evolution algebra
图9为采用NSGA-Ⅲ算法优化的Kriging组合模型裂纹参数真实值与识别值的对比。由图9可知,真实裂纹单元位于第58个有限元单元,裂纹位置的识别结果在第58单元和59单元,71%的识别结果处于第58单元;相对裂纹深度的识别结果在0.228~0.234范围内,真实相对裂纹深度为0.225,最大相对误差为2.6%,说明裂纹参数的识别效果好。
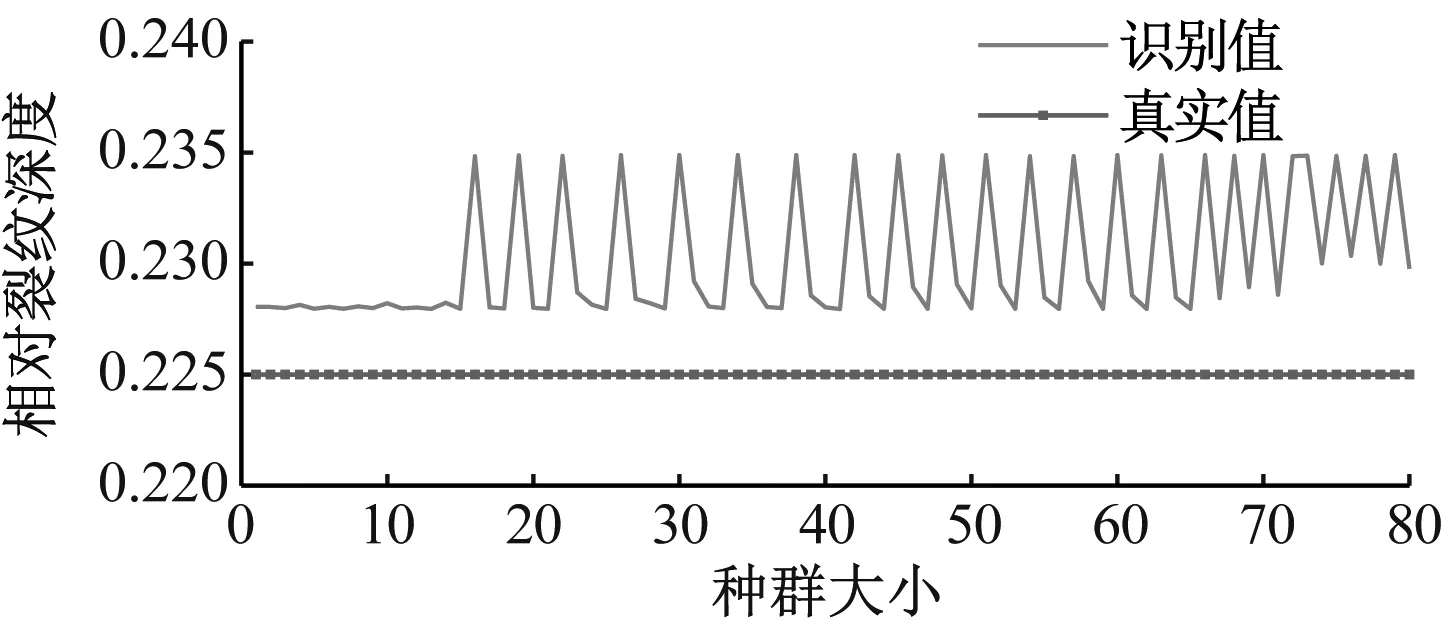
(b) 相对裂纹深度图9 最终种群中个体的裂纹参数分布Fig.9 Distribution of individual crack parameters in the final population
在转子裂纹参数识别中需要确定一组裂纹参数作为最终识别结果,因此,根据M的选择指标在Pareto最优解集中选取最佳裂纹参数,使识别的裂纹参数结果更加接近实际裂纹参数。图10为在Pareto最优解集中得到的种群中所有裂纹参数对应的M。由图10可知,在第55组中取得M的最小值,因此将Pareto最优解集中第55组作为最终识别的裂纹参数结果。另外4组也采用同样的过程,获取最终的识别结果。
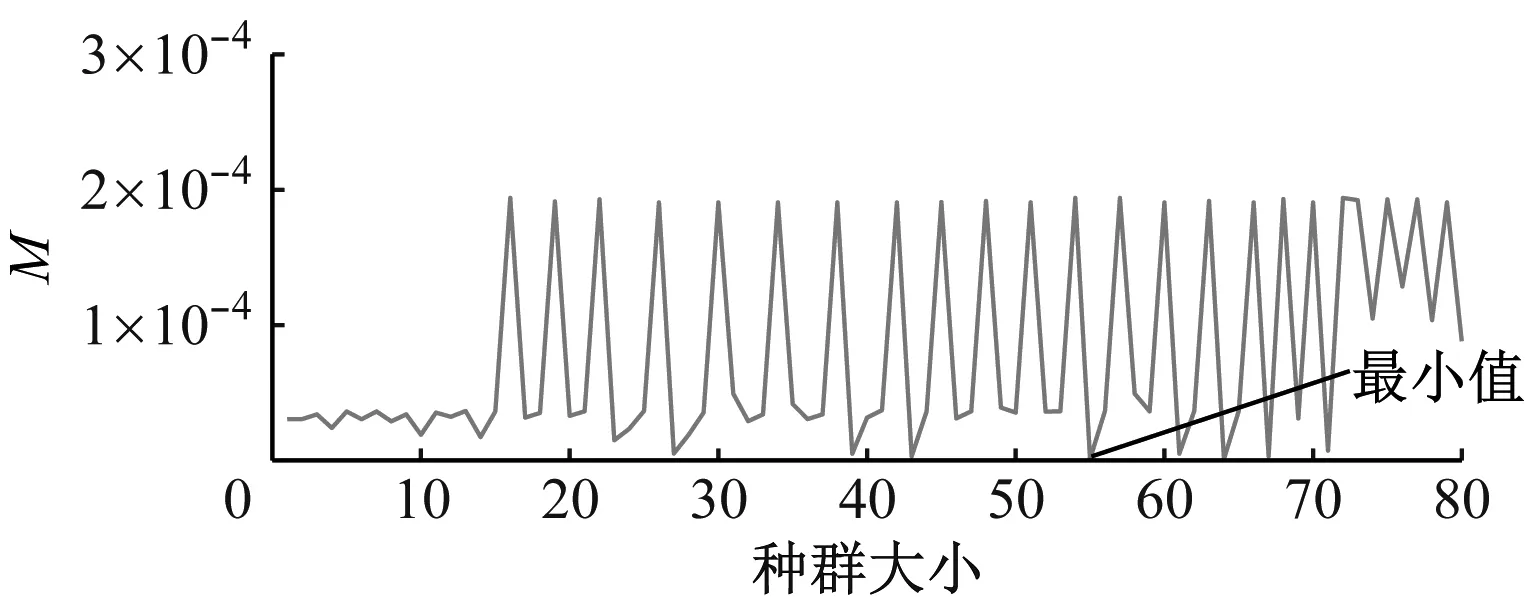
图10 裂纹识别结果的评价指标Fig.10 Evaluation indicators of crack identification results
满足M选择指标后的转子裂纹参数识别结果见表3。由表3可知,裂纹位置完全识别正确,相对裂纹深度的识别误差为0.15%~2.5%。综上,所提方法对转子系统的裂纹参数识别具有较高的有效性和准确性。
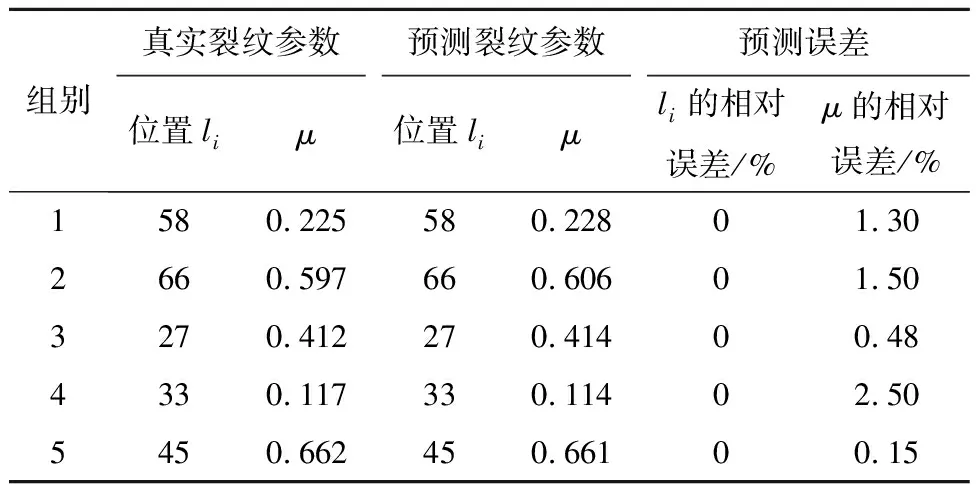
表3 转子裂纹参数识别结果
3.2 不同Kriging代理模型的识别对比分析
为了验证Kriging组合模型在裂纹参数识别中的精确性,采用基于单个Kriging代理模型的裂纹参数识别结果进行对比分析。此外,为证明所提Kriging组合模型(PESK)的优势,建立了考虑指数函数和高斯函数相结合的Kriging组合模型(ESK)[22],并与基于ESK模型的识别结果进行对比。对于基于不同Kriging模型最终预测识别结果的精度,使用平均绝对百分比误差(δMAPE)[23]分析真实值与识别值的误差,即
(28)
式中:s为总的识别组数;V为真实值;P′为预测识别值。
计算各验证样本裂纹参数的δMAPE,结果如图11所示。分析不同单个相关函数下Kriging代理模型与Kriging组合模型的识别误差,结果可知,基于Kriging组合模型的δMAPE最小,裂纹位置的δMAPE为0,相对裂纹深度的δMAPE为1.2%。综上分析可知,相较于单个Kriging代理模型的识别结果,基于Kriging组合模型的裂纹参数识别结果准确性较高。所提出的Kriging组合模型引入逐步回归模型筛选策略,解决了相关函数不确定性的问题,取得了比ESK组合模型更高的准确性。

图11 基于不同Kriging模型识别MAPE误差对比Fig.11 Comparison of identification MAPE errors based on different Kriging models
4 结 论
(1) 基于有限元和中性轴法理论,建立了裂纹转子系统的动力学仿真模型,获得了裂纹转子系统的1X、2X和3X超谐特征,并通过疲劳裂纹实验,验证了有限元动力学模型的正确性。
(2) 基于所提Kriging组合模型识别转子系统的裂纹参数具有很好的有效性和准确性,裂纹位置的识别完全正确,相对裂纹深度的最大识别误差为2.5%。
