束团相空间分布重建技术在西安200 MeV质子应用装置的应用

王敏文， 王忠明， 郑曙昕， 王 迪， 杨 业， 刘卧龙， 王百川，王茂成， 张 辉, 闫逸花， 吕 伟， 邱孟通， 邢庆子

(1. 强脉冲辐射环境模拟与效应国家重点实验室， 西安 710024； 2. 西北核技术研究所， 西安 710024；3. 清华大学 工程物理系， 北京 100084)

束流的相空间分布是粒子加速器的关键参数，在西安200 MeV质子应用装置(Xi’an 200 MeV Proton Application Facility, XiPAF)调试过程中，相空间分布的测量是比较加速器物理模型与实际模型的偏差及预测沿线束流包络分布的重要基础。三截面法和四极铁扫描法是被广泛应用的相空间分布间接测量方法[1-2]，通过测量3个截面重建束流相空间分布，具有对束流影响小、测量速度快的特点。由于三截面法和四极铁扫描法仅利用束流的均方根尺寸进行反推，只能得到束流相空间分布的Twiss参数。对束流分布做适当假设，可得到束流的相空间分布，但由于元件的非线性及空间电荷力等的影响，实际束流分布往往不是理想的高斯分布，束流相空间分布难以通过假设束流分布获得。为此，Hock等在不考虑非线性力的情况下，推导得到测量截面为待测相空间沿θ方向的投影，θ由待测点到截面探测器的传输矩阵决定[3]。因此，通过改变传输矩阵得到待测相空间沿不同方向的投影，结合断层重建技术可实现束流相空间分布的测量。在此基础上， Dimov等提出基于多粒子模拟的相空间重建方法，通过不断改变重建处的粒子分布，使模拟截面与测量截面趋于一致，实现了包含空间电荷力等非线性力影响的相空间重建[4]。本文采用基于多个1维截面迭代重建相空间方法，开展XiPAF直线段2维相空间的测量，并将该方法扩展应用到同步环纵向相空间分布的测量，为XiPAF的调试提供了有力支撑。

1 相空间迭代重建方法

传统基于1维截面重建束流2维相空间的方法多应用于空间电荷效应可忽略或空间电荷力可线性化近似的情况，此时，粒子沿束线的运动轨迹描述为

(1)

其中，M为重建点到截面探测器处的传输矩阵。

推导可得在截面探测器处测量的截面分布p(x)与待重建相空间分布ρ(x,x0′)的关系为[5]

(2)

p(x)=∬f(x,x0,x0′)ρ(x0,x0′)dx0dx0′

(3)

其中，f(x,x0,x0′)为从重建处到截面测量处的非线性传输函数，跟束流相空间分布ρ(x0,x0′)有关。因此，必须采用迭代的方法才可能根据多个p(x)求出ρ(x0,x0′)。假设，束流的水平和垂直方向相空间相互独立，迭代重建的思路是比较多个测量与模拟的截面，然后根据截面比较结果对重建点的相空间分布进行修正，直到模拟截面与测量截面趋于一致。具体迭代方法为：

1) 准备多组不同磁铁参数下或不同位置处测量的水平和垂直离散截面(以6组为例)。

2) 产生一个发射度远大于设计值的初始横向相空间分布，由于只重建束流横向相空间分布，初始束流纵向分布采用设计值。

3) 以初始相空间分布作为输入，利用基于PIC方法的多粒子动力学仿真软件分别模拟计算6组参数条件下截面探测器处的束流1维截面。

4) 由于束流的水平和垂直相空间分布是独立的，重建也是独立的，本文仅描述束流水平方向相空间分布的重建，垂直相空间分布重建类似。将测量截面按照面积为1进行归一化，并将模拟截面按照实际测量分辨率进行离散化，逐个比较6个测量与模拟截面，若模拟的粒子处于对应测量截面范围内，则该粒子对测量截面是有贡献的，称为有效粒子。找出每个模拟截面中的有效粒子集，取6个模拟截面有效粒子集的交集，即对每个测量截面均有贡献的粒子，作为最终的有效粒子集。

5) 逐个比较6个测量截面与仅包含有效粒子的模拟截面，用测量截面的幅度除以对应位置处模拟截面中的粒子数作为这些粒子在该截面的权重因子，将粒子在6个截面的权重因子求和作为该粒子最终的权重因子。

6) 通过粒子标识找到有效粒子在初始分布中的对应粒子，然后根据粒子的权重因子重新生成迭代分布。具体方法是根据粒子的权重因子和迭代分布的总粒子数N，在以该粒子的相空间坐标(x0,x0′)为中心、边长为d的正方形范围内随机添加N个粒子，其中d为重建步长，一般取测量截面的分辨率。

7) 利用新的初始粒子分布再次进行迭代，直到模拟截面与测量截面之间的偏差趋于收敛。

本文选用TraceWin进行束流横向动力学模拟，利用Python调用TraceWin实现交互，然后编写脚本进行截面的比较处理和初始粒子分布的重生成，实现了迭代过程的自动化。

2 直线加速器横向相空间重建

为验证上述迭代重建方法及研究测量截面位置对于相空间分布重建结果的影响，以图1所示直线段束线为例开展了数值仿真实验。该束线含5块四极铁(Q1,Q2,Q3,Q4,Q5)，重建中通过调整5块四极铁参数得到不同相移下的截面，利用这些截面和第1节提出的方法可重建束线起点处束流2维相空间分布。

图1 数值仿真实验束线布局Fig.1 Layout of the beamline for numerical experiment

测量截面的位置与待重建相空间分布的投影角度相关。文献[6]指出可用束流Betatron相移来对应相空间分布的投影角度，束流的Betatron相移对应于归一化相空间中相图的旋转角度，且在归一化相空间中的角度均匀采样映射到几何相空间就变成了沿相椭圆长轴方向附近的采样，可获得更多有效采样信息[3]。因此，使各测量截面对应的相移应尽量均匀，有利于得到更多有效投影信息，提高重建相空间分布的精度。

为验证上述结论，数值仿真实验选取了表1所列的3组截面进行重建。

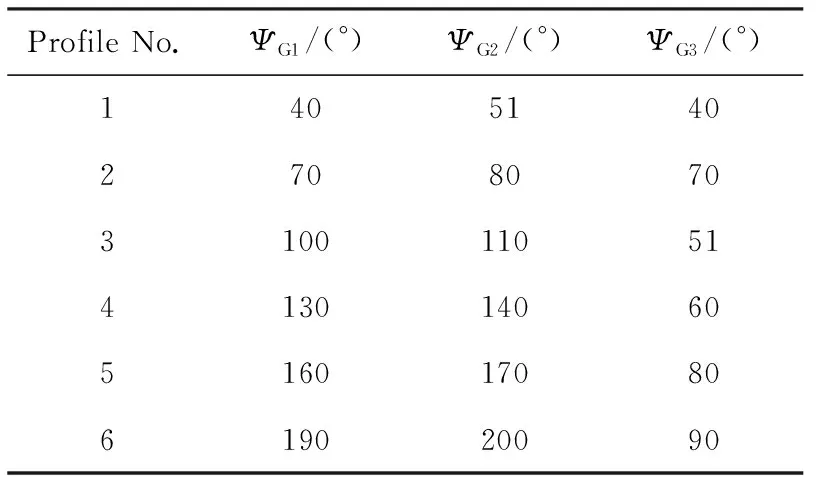
表1 不同组参数下各截面对应的相移Tab.1 Phase advances to different profiles

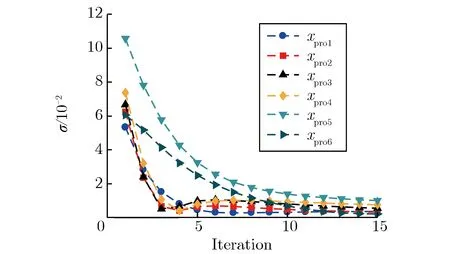
其中，G1和G2 6个截面对应相移在180°范围内均匀分布，但初始相移不同；G3 6个截面对应相移则仅在50°范围内均匀分布。横向相空间分布重建可2个方向同时进行，也可单方向独立进行，为便于描述，仅以水平方向的相空间分布重建为例。为符合实际测量情况，重建中截面的分辨率设置为0.1 mm。初始相空间分布均采用大发射度的均匀分布，重建截面的相对偏差随着迭代次数的变化，如图2所示。由图2可见，经过约10次迭代后，3组截面的偏差均达到收敛。

(a) G1

重建截面的相对偏差定义为

(4)

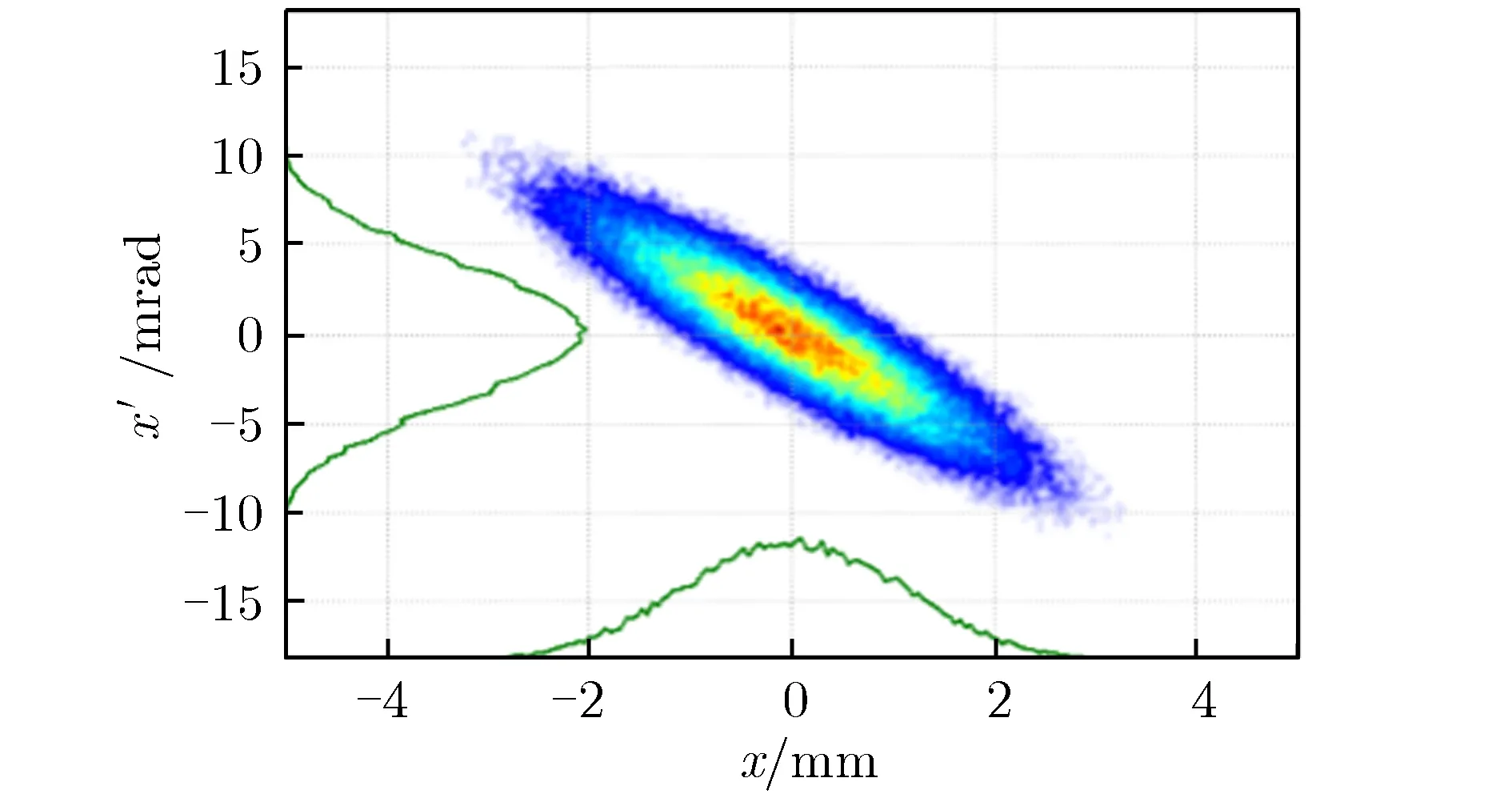
收敛后得到的重建相空间分布与参考相空间分布的比较，如图3所示。由图3可见，利用G1和G2截面较好地重建了束流2维相空间分布；G3截面由于相移分布范围较小，重建的结果存在较大偏差。表2为重建与参考相空间分布Twiss参数的比较。由表2可见，G1和G2重建结果的相对偏差在4%以内，G3重建结果的相对偏差达到了50%。模拟结果表明，为实现较好的相空间分布重建质量，测量截面的相移应在180°范围内尽量均匀分布。

(a) Reference

在XiPAF直线段开展了基于1维截面重建束流2维相空间分布的束流实验，并与发射度仪直接测量结果进行了对比，主要目的是测量漂移管加速器 (interdigit H-mode drift tube linac，IHDTL) 出口的束流参数。图4为XiPAF直线注入器的调试布局，在IHDTL后布置有3块四极铁用于束流横向匹配，四极铁后是1台双狭缝发射度仪，可测量束流截面，也可测量束流的相空间分布，因此2种方法的测量结果可以相互校验。与仿真过程类似，实验中通过调整3块四极铁参数使从IHDTL出口到截面探测器处束流的相移基本在180°内均匀分布，表3为XiPAF 1维截面重建发射度实验中束流水平和垂直方向各6组磁铁参数对应的相移。

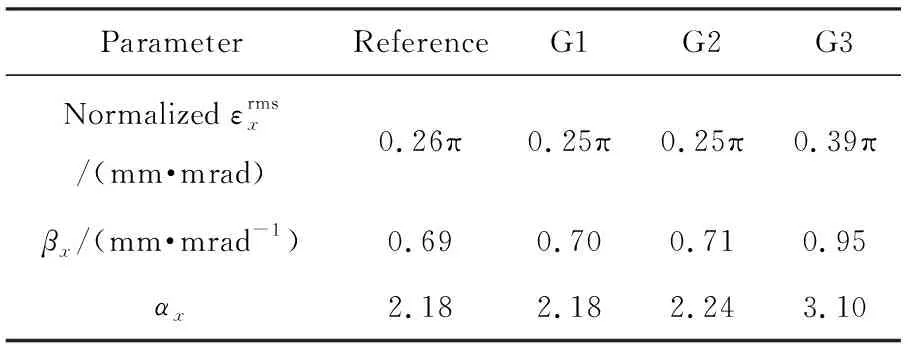
表2 重建与参考相空间分布的Twiss参数对比Tab.2 Comparison of Twiss parameters between reconstructed and reference phase spaces

图4 XiPAF直线段调试布局Fig.4 Layout of XiPAF linac

表3 XiPAF 1维截面重建发射度实验中束流水平和垂直方向各6组磁铁参数对应的相移Tab.3 Phase andvances corresponding to six groups of magnet parameters in the transerse directions in 1-D profile reconstruction emittance experiment at XiPAF

由于水平方向和垂直方向相空间分布测量时使用的四极铁参数不同，因此分别对水平和垂直相空间分布进行单独重建。重建水平方向相空间分布时，水平方向初始相空间分布为大发射度均匀分布的相空间分布，垂直方向初始相空间分布使用发射度仪测量得到的相空间分布，垂直方向相空间分布重建时亦然。由于狭缝宽度为0.1 mm，因此重建中截面测量分辨率也取为0.1 mm。重建截面与模拟截面的相对偏差随迭代次数的变化关系如图5所示。由图5可见，在约10次迭代以后，截面相对偏差趋于收敛。15次迭代后重建得到的IHDTL出口相空间分布，如图6所示。

(a) x direction

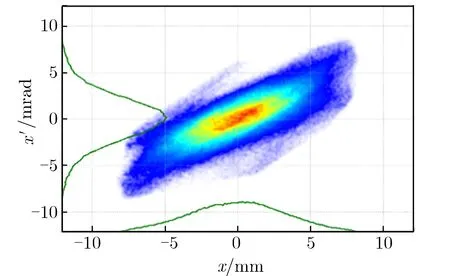
(a) x direction

为验证重建相空间的准确性，将发射度仪直接测量的结果反推得到IHDTL出口相空间分布，如图7所示。重建与发射度仪直接测量得到的IHDTL出口相空间Twiss参数的比较列于表4。除βy外，相对偏差均在±10%以内。发射度仪自身对于Twiss参数的测量偏差为±10%，由表4可见，2种方法的测量结果是相符的。

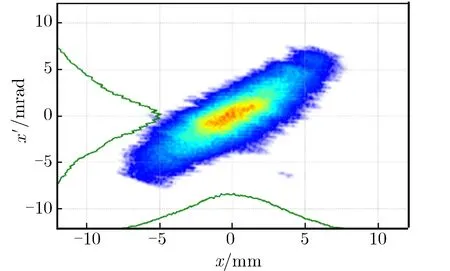
(a) x direction

表4 截面重建与发射度仪测量的IHDTL出口相空间Twiss参数的对比Tab.4 Comparison of reconstructed and measuredphase spaces at outlet of IHDTL

3 同步环纵向相空间重建

在质子同步环中，当空间电荷效应可忽略时，粒子的纵向运动可表示为[8]

(5)

其中，En和φn分别为第n圈粒子能量和相位；V为高频腔峰值腔压；Es和φs分别为同步能量和同步相位；h为谐波数；η为滑向因子；vnor为归一化速度；E0为粒子静止能量。由式(5)可见，纵向运动具有明显的非线性，且粒子偏离同步粒子越远，非线性越严重。因此，基于线性假设的断层重建方法不再适用。1节提出的迭代重建算法对于动力学计算过程没有任何限制，因此，将模拟束流横向运动的动力学程序替换为描述粒子纵向运动的式(5)，该迭代重建方法可应用到束流纵向相空间分布的测量。

在XiPAF中，采用快束流变压器(fast current transformer, FCT)[9]测量束流的逐圈纵向分布。根据动力学计算，环内束团均方根长度最小为8.5 ns，对应信号带宽在60 MHz以内，选择带宽为700 MHz的FCT进行束流纵向分布的测量。在储存不加速模式下，测量多圈束流包络，如图8所示。

图8 储存不加速模式下，测量的多圈束流纵向包络Fig.8 Measured multi-turn longitudinal profiles in storage mode

由于XiPAF同步环的纵向工作点较小，因此粒子需要绕环近1 000圈才能完成一次纵向振荡，为减少迭代算法的计算量，每隔50圈选取一个纵向截面，总计选取20个截面进行重建。重建与计算的俘获完成后束流的纵向相空间分布对比，如图9所示。

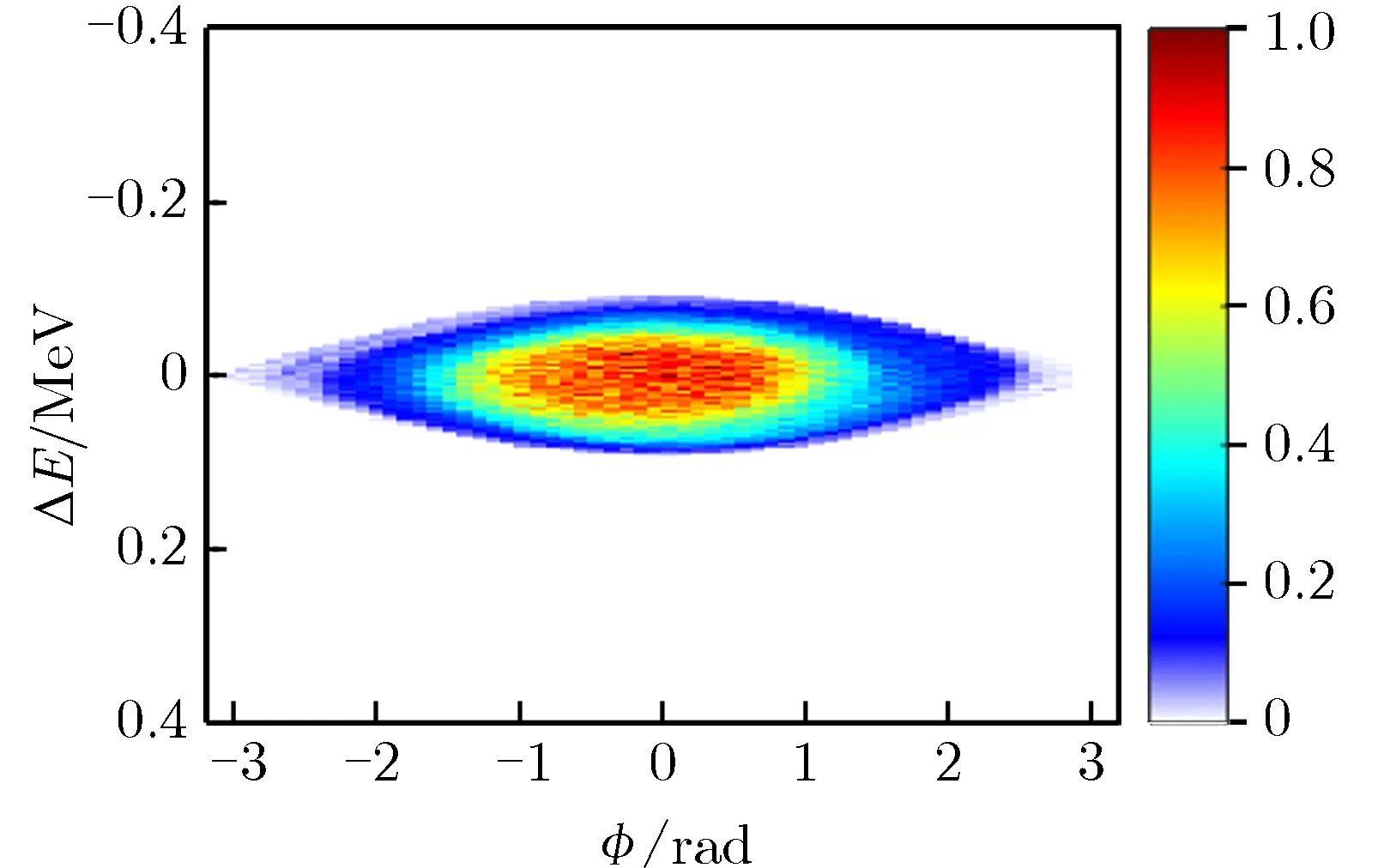
(a) Reconstructed phase space

由图9可见，由于储存不加速模式下仅对束流进行俘获而不加速，粒子分布几乎充满了整个相空间。表5为测量与模拟的纵向相空间分布Twiss参数比较。由表5可见，相对偏差在20%以内，验证了该方法的有效性。在束流加速到60 MeV平顶时，应用该方法重建得到的束流纵向相空间分布，如图10所示。

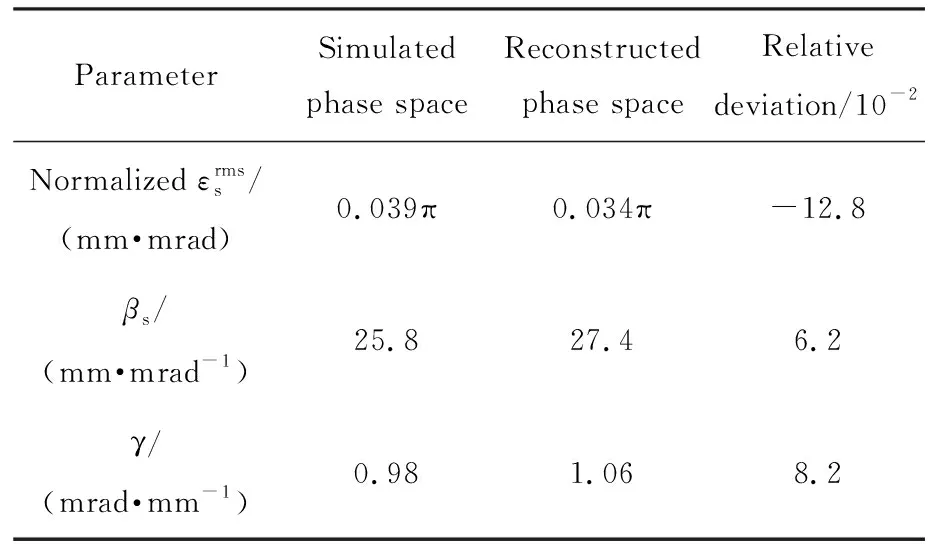
表5 测量与模拟的纵向相空间Twiss参数比较Tab.5 Comparison of the Twiss parameters ofreconstructed and simulated longitudinal phase spaces

图10 束流加速到60 MeV平顶时，重建得到的束流纵向相空间分布Fig.10 Reconstructed longitudinal phase spaceat 60 MeV beam flattop

4 结论

本文实现了一种基于多个截面重建束流相空间分布的迭代重建方法，与传统的三截面或四极铁扫描方法仅能在线性运动假设下测量束流的Twiss参数相比，该方法可应用于强空间电荷效应或非线性纵向运动等情况下束流相空间分布的测量，获得更多的束流信息。该方法成功应用于XiPAF直线段出口的束流水平方向2维相空间和同步环纵向相空间的重建，为加速器的调试提供了有力保障。