基于蒙特卡洛法的透平轮盘寿命计算及可靠性分析
2023-11-21李孝品田根起李思琦王家鋆
李孝品, 杨 宇, 田根起, 李思琦, 王家鋆
(上海发电设备成套设计研究院有限责任公司, 上海 200240)
自20世纪40年代起,燃气轮机凭借其高效、节能和低污染等优点,发展十分迅速并广泛应用于航空、航天、舰船、电力和能源等重大领域。透平轮盘是燃气轮机的关键热端部件之一,一般在高温、高压和高转速等恶劣环境下工作,承受着由本身高速旋转产生的离心力、振动及装配带来的应力以及轮缘部位与轮盘中心部位温度梯度所导致的热应力等。由于对燃气轮机整体性能指标的要求持续提高,透平轮盘的工作环境温度和转速也不断提高,导致透平轮盘承受的热载荷和循环机械疲劳载荷面临更加复杂的挑战。此外,轮盘的破坏大多会造成非包容性破坏,所引起的后果往往是一、二类事故[1]。因此,对透平轮盘的疲劳寿命和可靠性展开充分研究,是提高燃气轮机疲劳寿命和可靠性的关键依据和重要前提。
裴月等[2]通过对某型号发动机涡轮盘进行有限元分析计算,确定其薄弱部位,并基于Masson-Coffin公式完成了对不同工况下轮盘疲劳寿命的计算;同时,采用蒙特卡洛法结合响应面法,考虑涡轮盘的众多不确定性因素,计算得到涡轮盘的概率疲劳寿命和可靠性。Rathod等[3]基于线性累积损伤理论和P-S-N曲线,利用概率密度函数的一对一转换法则,建立了概率疲劳累积损伤模型。该模型不仅能应用于单应力水平载荷,同时也能应用于多应力水平载荷。Zhu等[4]考虑了材料响应的不确定性,基于Chaboche模型和Fatemi-Socie损伤标准建立了寿命预测模型,同时结合有限元计算与拉丁超立方抽样,完成了对试验数据、材料性能参数和载荷不确定性的量化,开发了涡轮叶盘的疲劳可靠性评估计算框架。
以上作者对寿命模型及可靠性分析方法进行了研究,但都缺乏实际试验数据验证。笔者重点开展了透平轮盘材料13Cr10MoW1VNbN的性能试验,对材料性能试验结果进行了分析,并采用Manson-Coffin公式基于材料试验数据拟合,建立了应变-寿命预测模型;通过文献查阅和试验数据,获得透平轮盘危险部位应力应变分布,分别应用蒙特卡洛法和包络线法获得透平轮盘的低周疲劳寿命数据样本,并进行了概率疲劳寿命计算及可靠性分析。
1 透平轮盘低周疲劳寿命模型
1.1 基于应力-应变的疲劳寿命预测
在高周疲劳寿命区域,弹性应力应变是导致结构失效的主要原因。根据胡克定律以及Basquin公式[5],弹性应力应变关系可表示为:
(1)
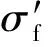
在低周疲劳寿命区域,塑性应力应变是导致结构失效的主要原因。塑性应变和寿命的关系可表示为:
(2)
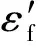
在实际工程应用中,弹、塑性应变同时存在,两者的区别仅在于塑性应变不能恢复,而弹性应变在一定条件下可恢复。Manson-Coffin公式可用来表示总应变和寿命之间的函数关系[6]:
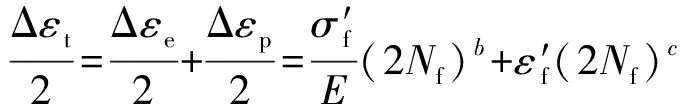
(3)
式中:εa为应变幅;Δεt为总应变变化量。
弹性应变和塑性应变的叠加为总应变,弹性应变、塑性应变、总应变与疲劳寿命之间的关系在双对数坐标系下可表示为图1所示[6]。
由图1可知,弹性寿命曲线与塑性寿命曲线交于一点,此处对应的寿命定义为过渡寿命Ng。
(4)
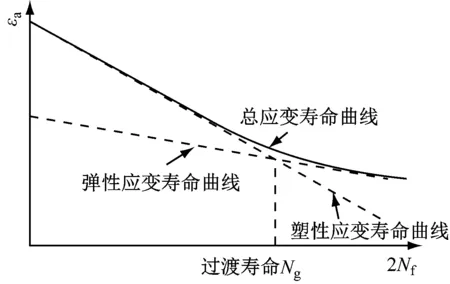
图1 总应变-寿命曲线Fig.1 Total strain vs life curve
1.2 透平轮盘材料性能试验
1.2.1 试验方法
选用透平轮盘轴向方向试样开展低周疲劳试验,参照GB/T 15248—2008 《金属材料轴向等幅低循环疲劳试验方法》进行试验。
采用13Cr10MoW1VNbN材料光滑圆柱形试样,试样在标距内为等截面的工作部分,具体尺寸见图2。
试验设备为INSTRON 8802-25T电液伺服低周疲劳试验机,应变引伸计型号为2620-602、2602-603,标距分别为12.50 mm和10.00 mm。所有设备试验前均经过校准,满足试验要求。
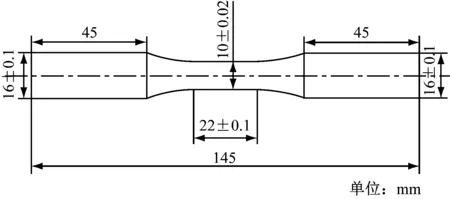
图2 低周疲劳试样Fig.2 Low-cycle fatigue test sample
1.2.2 试验控制参数及失效确定
从控制应变种类来看,低周疲劳试验可以选用控制总应变幅或控制塑性应变幅2种方式进行。从理论上看,疲劳损伤的本质是塑性变形,采用控制塑性应变幅进行试验更能揭示低周疲劳的规律,但从试验控制的角度,选择控制总应变幅更加方便[7]。
本试验采用总应变变化量Δεt作为控制参量,Δεt取0.4%、0.5%、0.6%、0.8%和1.0%,应变比为Rε=-1,试验波形为三角波。由于材料低周疲劳性能具有起始加载效应,试验时可选择从相同的半循环(拉伸)开始。
试验通常采用恒定的加载速率或恒定的频率,本试验采用恒定应变速率加载方式,应变速率控制在0.001~0.004 s-1内。
试样失效前所加载荷循环次数即为该试样的疲劳寿命Nf,本试验过程中以荷载下降20%作为失效依据。但试验过程中也出现了其他失效与无效现象,如试样发生弯曲或断在引伸计标距以外,此种情况得到的结果为无效数据。
1.2.3 试验结果与分析
试样承受循环载荷时的应力-应变关系如图3所示,这样的应力-应变迹线称为迟滞回线,图中σ为应力,εt为总应变。通常,恒幅载荷下的迟滞回线在开始阶段是变化的,随着循环次数的增加,逐渐趋于稳定,约在失效循环次数Nf的20%~50%时形成稳定迟滞回线,本试验选择0.5Nf作为稳定循环周次N。
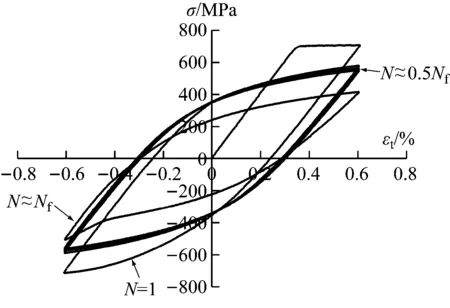
图3 循环加载时的应力-应变曲线Fig.3 Stress vs strain curves under cyclic loading
图4为加载过程中循环应力Δσ与初始应力σs之比随加载次数的变化情况,在应变控制的低周疲劳过程中,由于材料是典型的循环软化材料,所以开始加载后便呈现出明显循环软化特性。循环软化特性可以分为3个阶段,即循环应力幅快速下降的软化阶段(I)、循环应力幅近乎匀速下降的相对稳定阶段(II)和循环应力幅再次快速下降的阶段(III),分别对应裂纹起始阶段、微裂纹稳定增长阶段和宏观裂纹的增长阶段。整个循环过程中,没有看到明显的应力饱和现象。
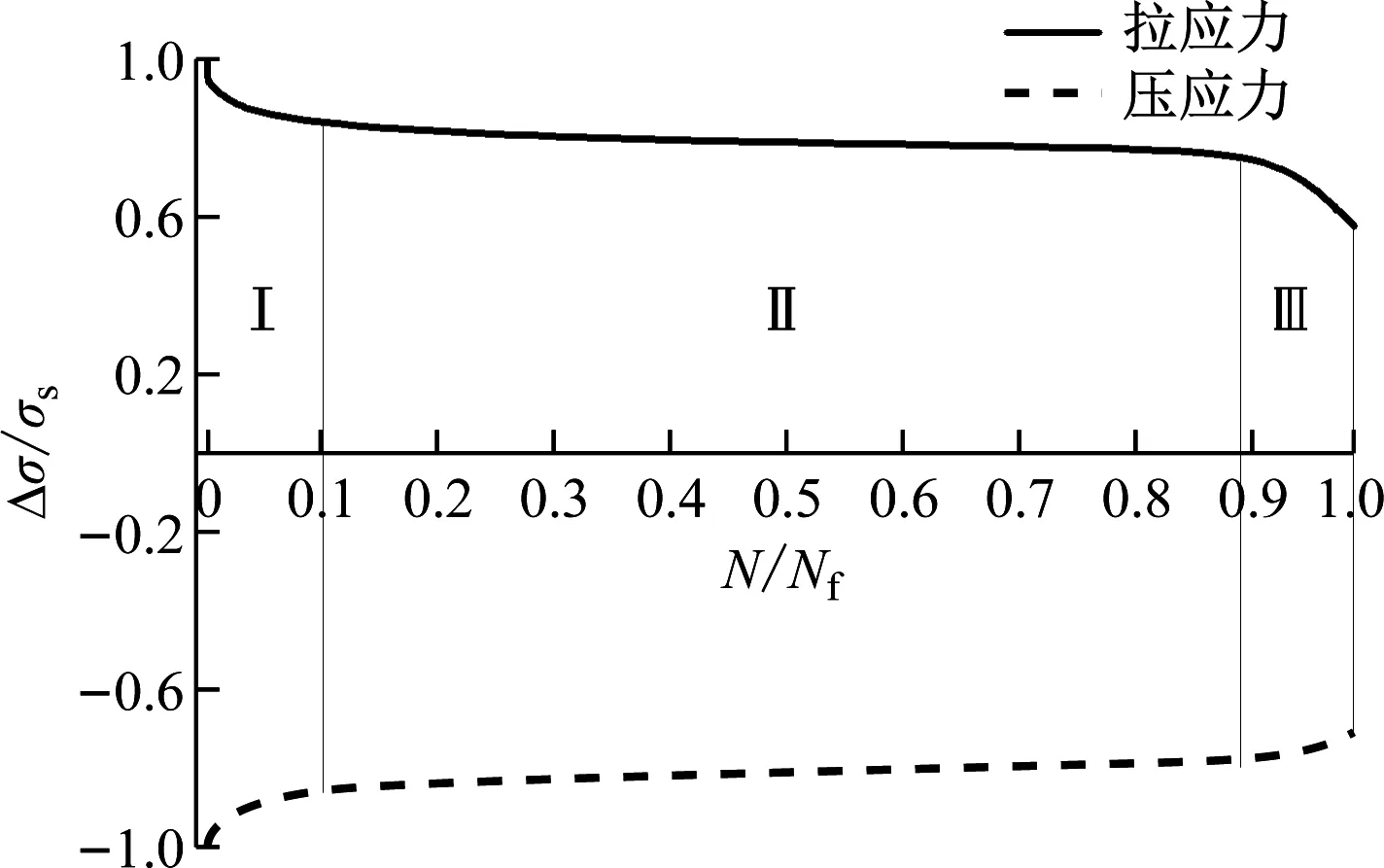
图4 峰值和谷值应力随循环周次的变化Fig.4 Variation of peak and valley stress with cycle times
材料的循环应力-应变曲线是对试样采用不同总应变变化量Δεt进行循环加载,得到不同Δεt下的相应稳定迟滞回线。最后通过各稳定迟滞回线顶点画出1条光滑曲线,即得到所求的循环应力-应变曲线。就其物理意义讲,循环应力-应变曲线上各点分别表示材料在循环载荷作用下应力幅值与应变幅值的一一对应关系。
循环应力-应变曲线[7]符合以下表达式:
(5)
循环稳定应力幅Δσ/2与塑性应变幅Δεp/2之间符合下式:
(6)
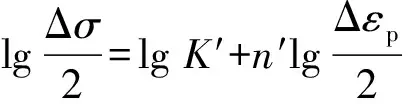
(7)
式中:K′为循环强度系数;n′为循环应变硬化指数。
(8)
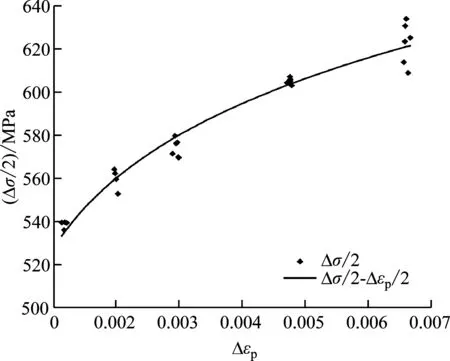
图5 循环稳定曲线Fig.5 Stably cyclic curve
则稳定循环应力应变方程为:
(9)
对应的循环应力应变曲线如图6所示。
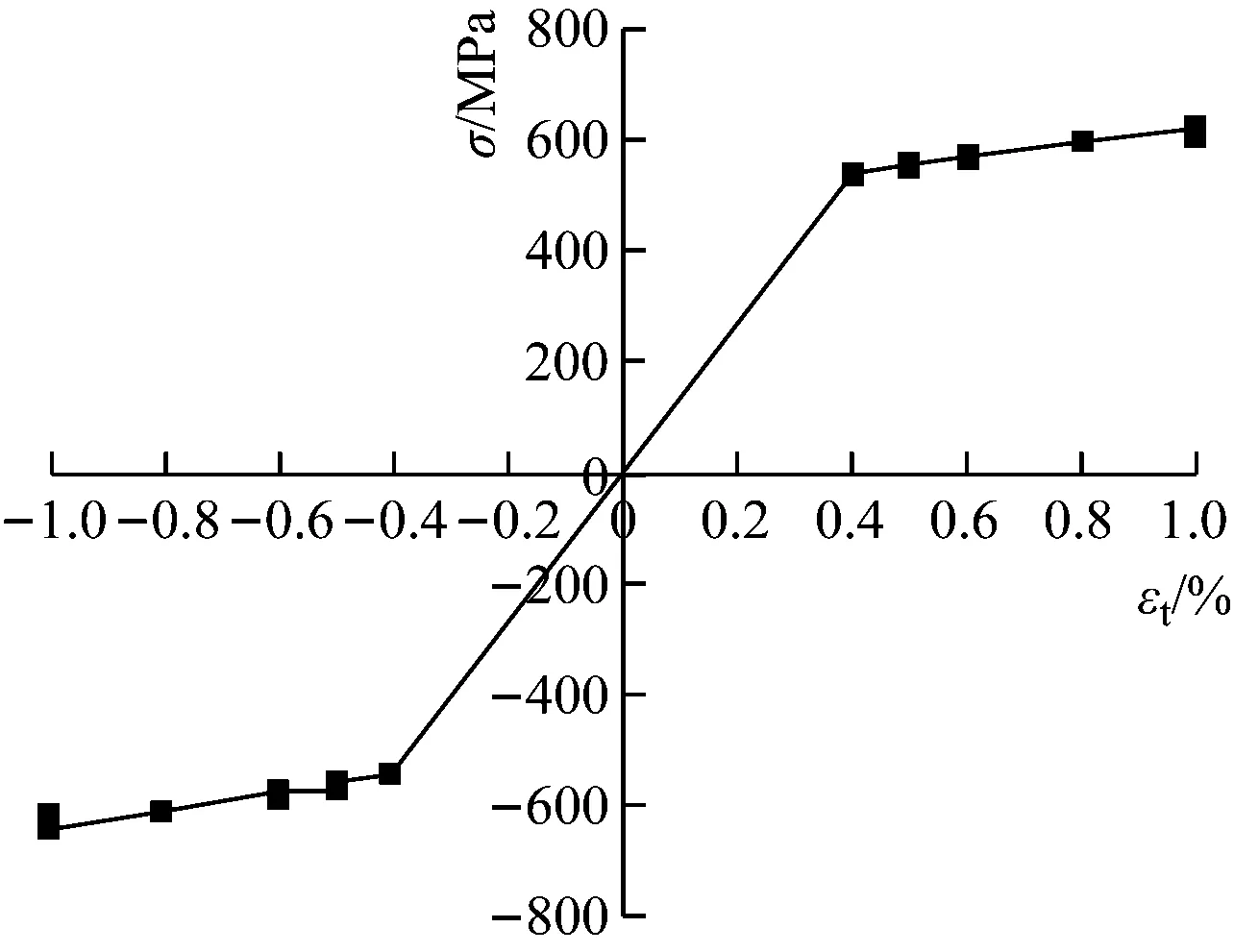
图6 循环应力-应变曲线Fig.6 Cyclic stress vs strain curve
1.2.4 试验结果误差分析与优化
采用13Cr10MoW1VNbN材料光滑圆柱形试样,与轮盘结构差异较大,为减少将试验结果运用到计算轮盘寿命时的偏差,可考虑使用等效应力-应变模型[6]。
等效应力-应变模型是将单轴理论拓展到多轴疲劳破坏理论中,把复杂的多轴问题转化为简单的单轴问题来解决。其中,Von Mises 准则[6]是等效应力-应变模型的代表,其假设材料的损伤断裂由等效应力-应变导致,表达式为:
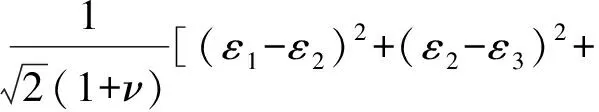
(ε3-ε1)2]0.5
(10)
式中:εi(i=1,2,3)为主应变幅值;εeq为等效应变;ν为泊松比。
在通过有限元计算获得轮盘在运行工况下的应力应变分布后,可通过上式修正计算得到等效应力应变,并代入寿命模型计算,以减少试验条件限制带来的误差。
另一方面,本文试验为常温常压环境,而燃气轮机透平轮盘通常在高温高压环境下工作。虽然将该材料在常温常压下的试验数据及结论运用到实际工作环境下仍具有可行性,但为了提高研究成果的普适性,可采取改进四点关联法[7]对材料疲劳参数进行修正,如式(10)所示。
(11)
式中:εf为断裂延性系数;σb为强度极限;σf为真实断裂强度。
1.3 疲劳寿命模型参数
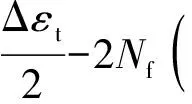
通过稳定迟滞回线可以看出,应变幅Δεt/2可分解为塑性应变幅Δεp/2和弹性应变幅Δεe/2。故总应变曲线可分解成塑性线和弹性线2条曲线。且2条曲线在双对数直角坐标系中可近似地看成2条直线。以上3条曲线的关系式[8]分别见式(1)、式(2)和式(3)。
测定应变-寿命曲线时,采用一组20~30根相同的试样,选取5个总应变幅Δεt/2的值,对各试样进行恒应变循环加载试验,在双对数曲线中拟合出低周疲劳寿命模型各参数值,如表1所示。
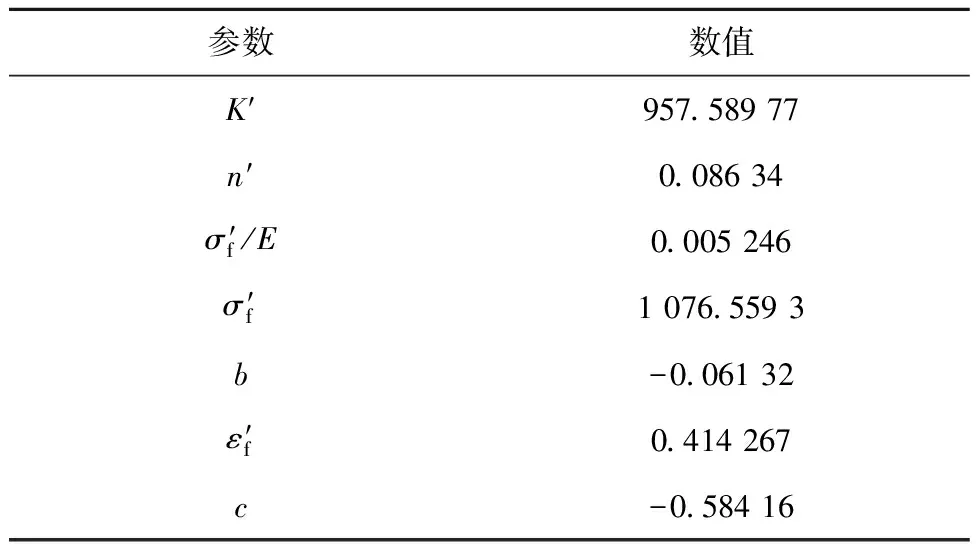
表1 疲劳寿命模型参数
将各参数代入Manson-Coffin公式得:
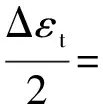
(12)
上式在双对数坐标系中各应变-寿命曲线如图7所示。
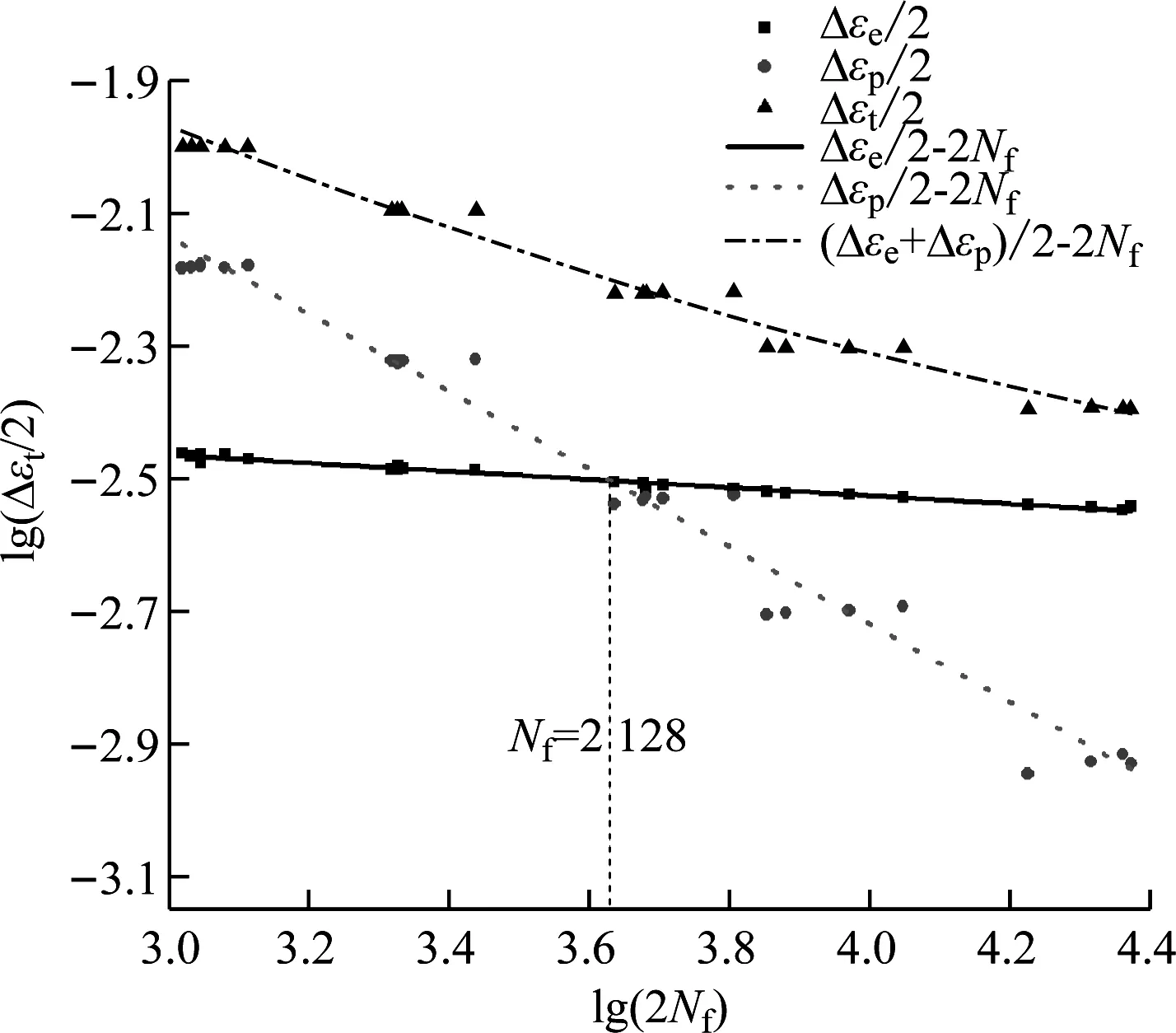
图7 应变-寿命曲线Fig.7 Strain vs life curves
2 概率疲劳寿命计算方法
2.1 蒙特卡洛法
蒙特卡洛法也称统计模拟试验法,通过对随机变量抽样从而估计和描述函数的统计量,进而确定其分布[9]。通过计算获得应变样本数据后,对样本数据分布进行处理,再运用蒙特卡洛法对样本数据进行随机模拟抽取。蒙特卡洛法解决此类问题包括以下步骤:
(1) 构造概率模型。在本文中,自变量等效应变的概率分布服从正态分布模型,且取:
Δεt/2~N(0.004,0.000 1)
(2) 定义随机变量。构造多个独立自变量与因变量的函数关系,即定义疲劳寿命模型。
(3) 通过模拟获得子样。根据各自变量的分布特征产生随机数,通过步骤(2)中的函数关系,采用牛顿迭代法求解疲劳寿命。
(4) 统计计算。对第(3)步中的样本进行参数估计,得到寿命的数字特征与概率分布。经计算,所获疲劳寿命样本数据服从正态分布,即
Nf~N(11 732.39,982.67)
2.2 包络线法
由于运行参数、载荷分布和边界条件等不确定因素的影响,部件的应力应变不是一个定值,而是服从某一分布。即
Δεt/2~N(0.004,0.000 1)
另一方面,考虑到材料性能参数也具有一定分散度,根据P-S-N曲线的定义[10-11],由试验数据可拟合得到各存活率P下的εt-N曲线。
综合考虑运行参数、载荷分布等不确定性因素对应变分散度的影响,以及材料参数的分散度,可选取图8所示特殊样本点作为疲劳寿命样本数据进行统计计算,并完成可靠性分析。
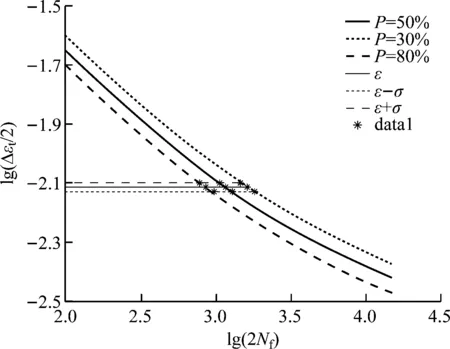
图8 包络线及特殊样本点Fig.8 Envelope and special sample points
3 可靠性分析
蒙特卡洛采样方法是在计算机的辅助下基于数学方法产生的,与包络线法相同,都是先对疲劳寿命数据进行分布假设,所以需要对寿命样本概率分布进行假设检验。笔者采取χ2(卡方)检验、Jarque-Bera检验、Kolmogorov-Smirnov检验(K-S检验)和Lillietest检验4种检验方法[9],检验结果见表2。由表2可知,χ2检验、K-S检验以及Lillietest检验返回值均为0,接受原假设,即认为3种方法获得的数据均服从正态分布。

表2 假设检验方法及结果
设x是透平轮盘在规定运行条件下的低周疲劳寿命,则“透平轮盘在规定时间XR内完成规定功能”的事件与“透平轮盘低周疲劳寿命x>XR”的事件是等价的[12]。给定任意一个XR,它所对应的可靠度R可以看成是事件x>XR的概率,即
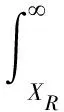
(13)
x=N服从正态分布,有:
(14)
(15)
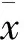
令
(16)
(17)
则有
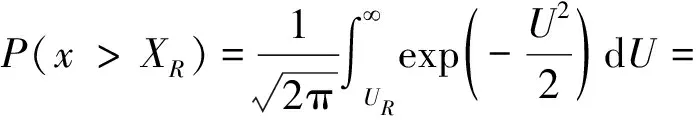
1-φ(UR)
(18)
其中,φ(z)为标准正态概率分布函数。
(19)
基于蒙特卡洛法的可靠度R1为:
(20)
基于包络线法的可靠度R2为:
(21)
根据以上公式可得到燃气轮机透平轮盘基于蒙特卡洛法和包络线法的可靠度曲线,如图9所示。从图9的整个变化趋势来看,基于蒙特卡洛法的可靠度R1曲线比基于包络法的可靠度R2曲线下降更为平缓。R1在疲劳周次为7 000左右时可靠度开始下降,随着疲劳周次的不断增大,可靠度不断降低,直到疲劳周次为16 000时接近0。R1的安全裕度大约在疲劳周次为9 000时。对于R2来说,在疲劳周次为9 000时其可靠度开始下降,下降趋势比R2迅速,直到14 000周次时接近0,安全裕度大约为5 000周次。
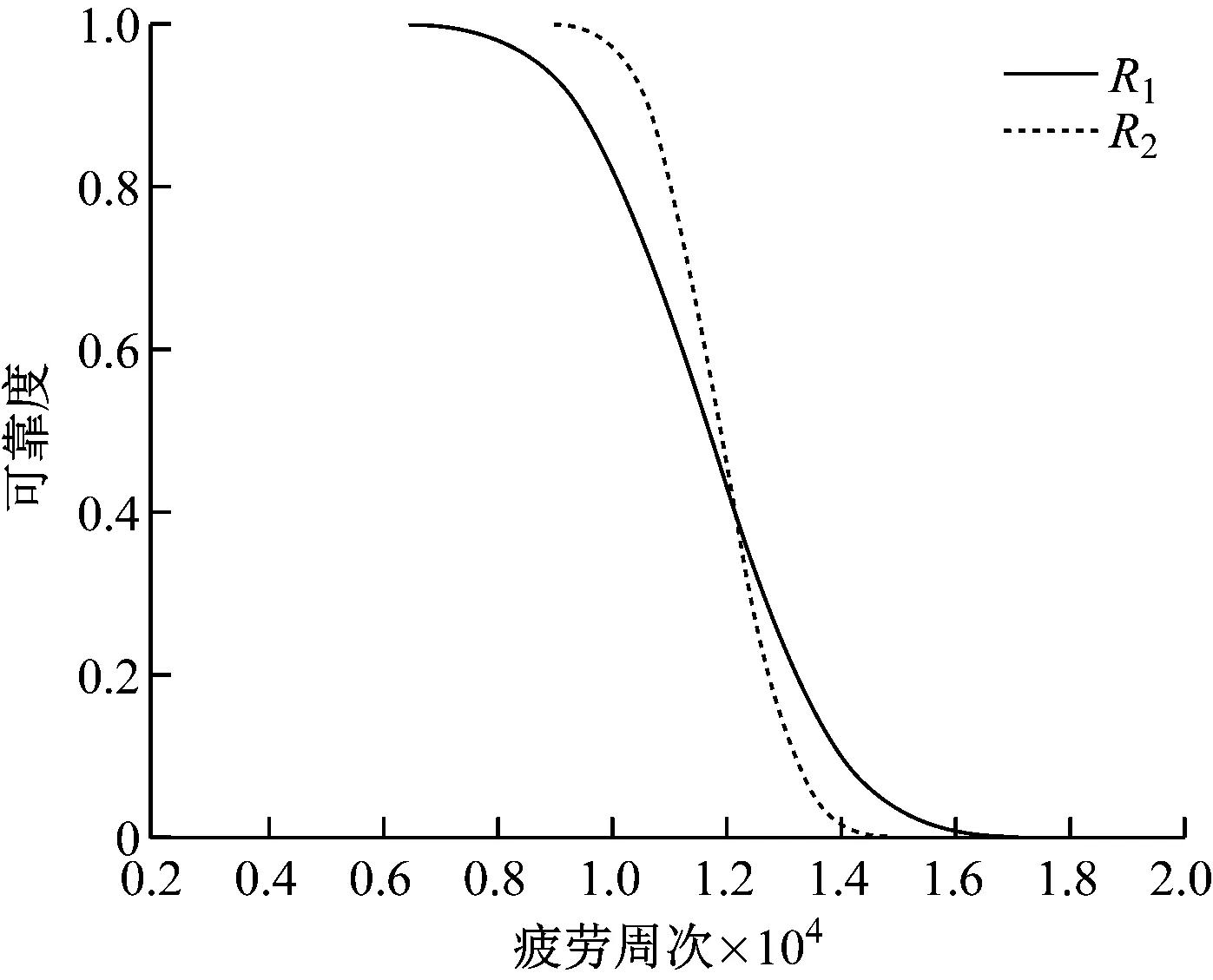
图9 可靠度曲线Fig.9 Reliability curves
另一方面,在曲线下降的前半段,相同时间下R1比R2小;而在曲线下降的后半段,由于R2下降趋势更为陡峭,相同时间内R2比R1小。
分析造成这种差异的原因为:(1) 基于蒙特卡洛法所获得的疲劳寿命数据样本容量大,且疲劳寿命服从正态分布的均值较小而标准差较大;(2) 蒙特卡洛法不仅考虑了运行参数、载荷分布的不确定性,还考虑了材料参数的不确定性对可靠性的影响。可见,基于蒙特卡洛法获得的可靠度曲线考虑更加全面。
4 结 论
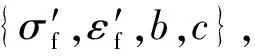
(2) 基于蒙特卡洛法及包络线法,并采用牛顿迭代方法计算透平轮盘低周疲劳寿命,获得透平轮盘低周疲劳寿命数据样本,分别进行了假设检验与统计分析,检验结果表明2种方法获得的疲劳寿命均服从正态分布。
(3) 进行了可靠度曲线的计算并展开分析。相比于包络线法,蒙特卡洛法获得的可靠度曲线下降趋势更加缓慢,考虑的不确定性因素更加全面,安全裕度更大。
