基于改进灰狼算法的热电联供系统负荷优化分配策略研究
2023-11-21司风琪
丁 衡, 胡 慧, 曹 越, 孙 健, 司风琪
(1. 东南大学 能源热转换及其过程测控教育部重点实验室, 南京 210096; 2. 内蒙古京隆发电有限责任公司, 内蒙古丰镇 012100)
近年来,随着我国各地区采暖需求逐步增加及风电、光伏等可再生能源的迅速发展[1],部分火力发电企业为提升发电竞争力与盈利能力,对纯凝机组进行了供热改造。然而,在多台热电联供机组联合供热情况下,因不同机组间热力性能存在差异,研究给定的热电负荷总指令下,各机组间热电负荷的最优分配方式,以实现系统经济效益和可再生能源消纳能力最大化具有非常重要的意义[2-3]。
李坤[4]提出了一种基于模糊集空间划分的改进多目标粒子群优化算法,并对区域内多个热电联产机组的电热负荷分配问题进行研究。韩中合等[5]从热经济学和经济学角度出发,以单位输出功率的系统总投资成本和系统产品单价为目标函数构建了多目标优化模型,并采用多目标优化灰狼算法(MOGWO)对模型进行求解。李军等[6]针对某电厂多机型、多热源的复杂机组,提出了一种改进的遗传算法,对该机组进行负荷优化分配。Kang等[7]利用遗传算法对热电联供系统与热泵系统相结合的新型耦合系统的发电量、热泵出口温度等关键参数进行优化,使其综合性能最大化。许可[8]建立了汽轮机侧和锅炉侧的热电负荷优化分配目标函数,分别为汽轮机发电汽耗率和锅炉产汽煤耗率最低,利用蚁群算法对其进行求解,以获得最佳负荷分配方式。Çetin等[9]采用模拟退火算法对某电厂仿真模型中的17个优化参数同时进行优化,使其达到最大效率。卫治廷等[10]采用黏菌优化算法,以先汽机侧、后锅炉侧的顺序,对某“三炉两机”母管制热电联产机组进行负荷优化分配。韩朝兵等[11]提出了一种改进的混沌粒子群算法,并将其应用于考虑汽轮机阀点效应的火电厂经济负荷分配模型中。目前,多种优化算法均被运用到热电负荷优化分配研究中,随着深入研究,各类优化算法也在不断被改进,以提高寻优性能并降低时间成本。
笔者针对传统灰狼优化算法中繁琐的更新机制导致的时效性差等问题,提出了一种改进的多目标灰狼算法(MOGGWO),并将该算法应用于某600 MW双机热电联供系统的多目标热电负荷优化分配策略研究中,以提高系统的运行经济性和可再生能源消纳能力。
1 系统概况
以某电厂600 MW双机热电联供系统为研究对象,包括1台600 MW的高背压抽凝供热机组、1台600 MW的抽凝供热机组以及热网首站等设备,其系统图如图1所示。
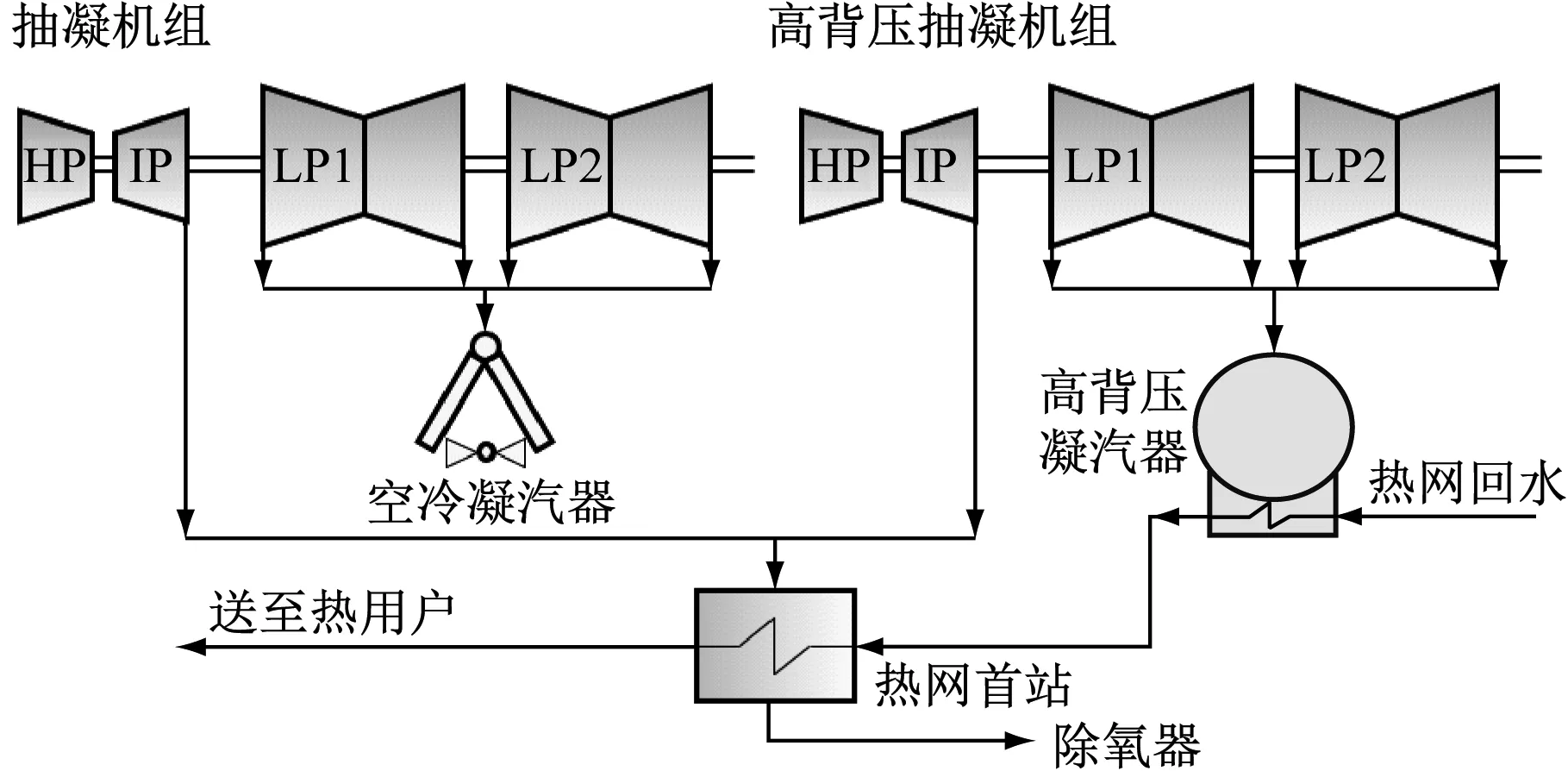
图1 600 MW 双机热电联供系统图Fig.1 Diagram for the CHP system consisting of two 600 MW units
抽凝机组通过从汽轮机中压缸末级抽取部分蒸汽对外供热,高背压抽凝机组则在抽凝机组的基础上增加了高背压乏汽加热热网循环水,充分利用了机组排汽的汽化潜热,以提高机组循环热效率,最终在热网首站中,热网循环水被2台机组的中间抽汽进一步加热,升温至所需温度后送至热用户。
2 热电负荷分配模型
2.1 目标函数
选取机组热耗量Qtp作为热经济性评价指标,其数学模型为:
(1)
式中:Btp为总燃料消耗量,kg/s;qnet为燃料低位发热量,kJ/kg;Q0为汽机总热耗量,MW,由式(2)计算得到;ηb、ηp分别为锅炉效率和管道效率。
(2)
式中:qm、qm,fw、qm,zr、qm,lz、qm,jws分别为主汽质量流量、给水质量流量、再热蒸汽质量流量、冷再热蒸汽质量流量和减温水质量流量,kg/s;h0、hfw、hzr、hlz、hjws分别为主汽焓、给水焓、再热蒸汽焓、冷再热蒸汽焓和减温水焓,kJ/kg。
所研究的热电联供系统包含高背压抽凝机组和抽凝机组,则系统总热耗量Qtp,D可表示为:
Qtp,D(PD,GD)=Qtp,1(P1,G1)+Qtp,2(P2,G2)
(3)
式中:PD、P1和P2分别为总电负荷指令、高背压抽凝机组电负荷和抽凝机组电负荷,MW;GD、G1和G2分别为总热负荷指令、高背压抽凝机组热负荷和抽凝机组热负荷,MW;Qtp,1、Qtp,2分别为高背压抽凝机组和抽凝机组热耗量,MW。
定义可再生能源消纳容量表达式如式(4)所示,以定量表示热电联供机组在不同工况下的可再生能源消纳能力。
PREC=P-Pmin(G)
(4)
式中:PREC为可再生能源消纳容量,MW;P为机组电负荷指令,MW;Pmin(G)为热负荷为G时机组最小电功率函数。
热电联供系统的可再生能源消纳容量PREC,D可表示为:
PREC,D(PD,GD)=PREC,1(P1,G1)+PREC,2(P2,G2)=P1+P2-(Pmin,1(G1)+Pmin,2(G2))
(5)
式中:PREC,1、PREC,2分别为高背压抽凝机组和抽凝机组的可再生能源消纳容量,MW;Pmin,1(G1)为高背压抽凝机组热负荷为G1时的最小电功率函数;Pmin,2(G2)为抽凝机组热负荷为G2时的最小电功率函数。
综合考虑系统经济性和可再生能源消纳能力,建立多目标热电负荷优化分配模型。多目标优化的显著特点是优化各个目标使其同时达到综合最优值,该600 MW双机热电联供系统的热电负荷优化分配目标为:在给定的总电、热负荷指令(PD,GD)条件下,实现系统总热耗量Qtp,D最小化及可再生能源消纳容量PREC,D最大化。
2.2 约束条件
热电负荷优化分配模型的约束条件主要为各机组及系统的热电负荷可行域。
机组热电负荷可行域除受汽轮机最大进汽量、锅炉最小蒸发量及低压缸最小凝汽量限制外,笔者还综合考虑了机组中排压力限制、高背压供热机组允许投入抽汽限制和乏汽利用裕量边界,更贴合现场实际运行情况。
抽凝机组的热电负荷可行域如图2所示。图中A2B2为汽轮机最大进汽量工况线,与之平行的均是主汽质量流量一定时电功率随供热量的变化曲线,且主汽质量流量从A2B2逐渐递减至锅炉最小蒸发量工况线E2F2。A2E2为纯凝工况线,B2D2F2为低压缸最小凝汽量工况线,此时供热量达到了各主汽质量流量下的最大供热量。C2D2为抽汽供热压力转折工况线,该工况线对应的主汽质量流量为1 615 t/h,当主汽质量流量大于该值时,抽汽供热压力最大可达上限值1.15 MPa,当主汽质量流量小于该值时,为保证中排温度不超限,最大抽汽供热压力随主汽质量流量的减小而逐渐降低。
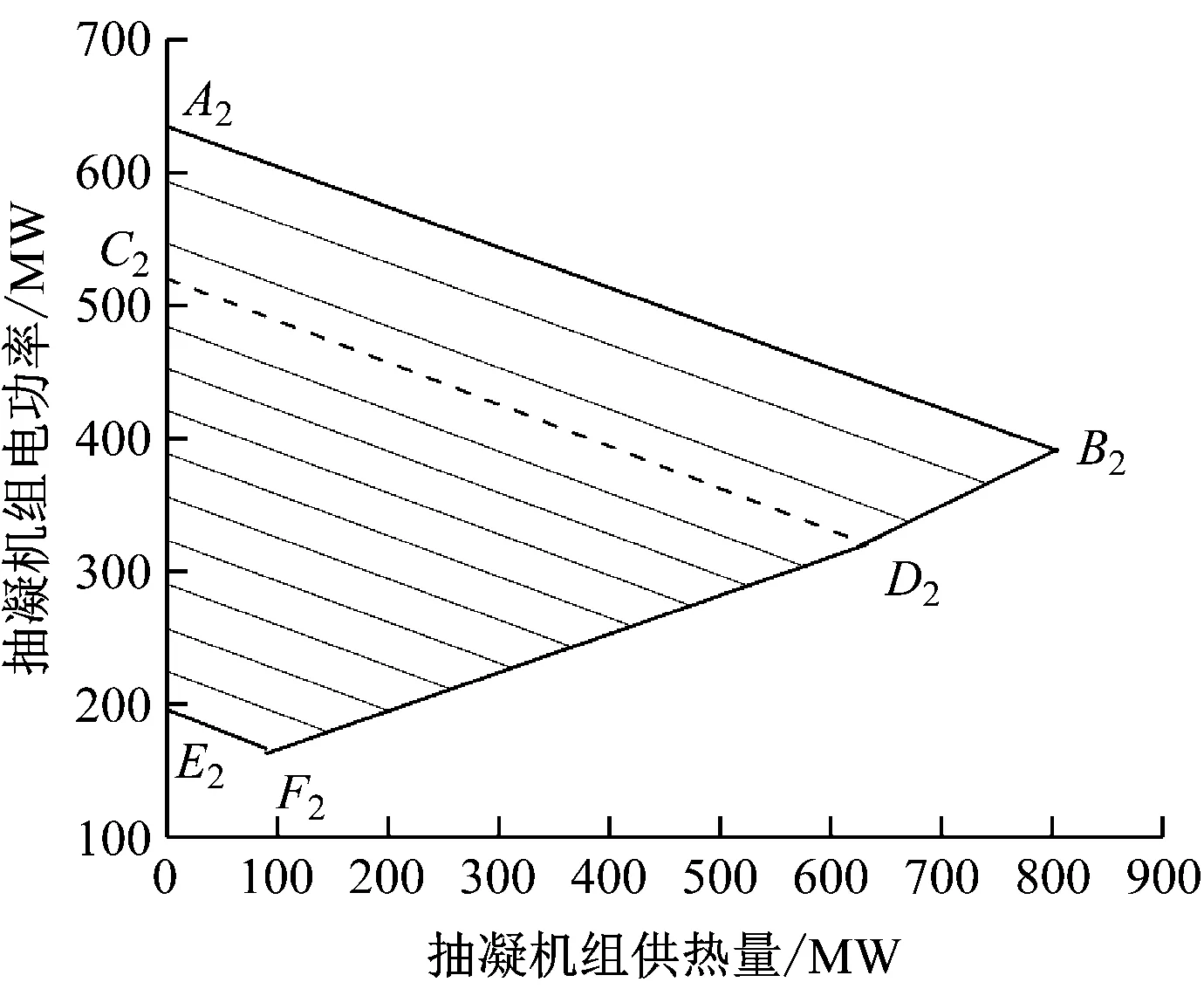
图2 抽凝机组热电负荷可行域Fig.2 Feasible range of thermoelectric load of condensing unit with intermediate extraction
高背压抽凝机组的热电负荷可行域如图3所示。其中A1B1C1为汽轮机最大进汽量工况线,与之平行的均是主汽质量流量一定时电功率随供热量的变化曲线。A1K1L1为乏汽供热工况线,此时抽汽供热质量流量为0 t/h,其中A1K1段因主汽质量流量较大,使得低压缸排汽量较大,乏汽供热量达到了高背压凝汽器最大负荷490 MW,剩余排汽进入空冷凝汽器,且空冷进汽量随主汽质量流量的减小而逐渐减小至空冷最小防冻流量,如工况点K1所示,此后K1L1段因主汽质量流量进一步减小,乏汽供热量无法满足490 MW,因此供热量随电功率减小(主汽质量流量减小)而逐渐减小至锅炉最小蒸发量工况点L1。G1H1J1为机组允许投入抽汽临界工况线,此时调节级后压力为8.152 MPa,对应的主汽质量流量为1 279.45 t/h,当机组调节级后压力小于该临界值时,机组仅具备乏汽供热能力,如G1K1L1工况线所示。C1F1J1为低压缸最小凝汽量工况线,此时供热量达到了各主汽质量流量下的最大供热量。D1E1F1为抽汽供热压力转折工况线,此时主汽质量流量为1 610 t/h,当主汽质量流量大于该值时,抽汽供热压力最大可达上限值1.15 MPa,当主汽质量流量小于该值时,为保证中排温度不超限,最大抽汽供热压力随主汽质量流量的减小而逐渐降低。B1E1H1为乏汽供热量转折工况线,A1B1E1H1G1A1区域内工况供热抽汽量较小,低压缸排汽量较大,在满足高背压凝汽器最大热负荷的前提下,还有剩余蒸汽进入空冷凝汽器,且空冷进汽量随着供热抽汽量增大而逐渐减小至空冷最小防冻流量,B1C1F1J1H1E1B1区域内工况供热抽汽量进一步增大,在保证空冷最小防冻流量的情况下,高背压凝汽器进汽量逐渐减小,因此该区域内乏汽供热量随供热抽汽量增大而逐渐减小。
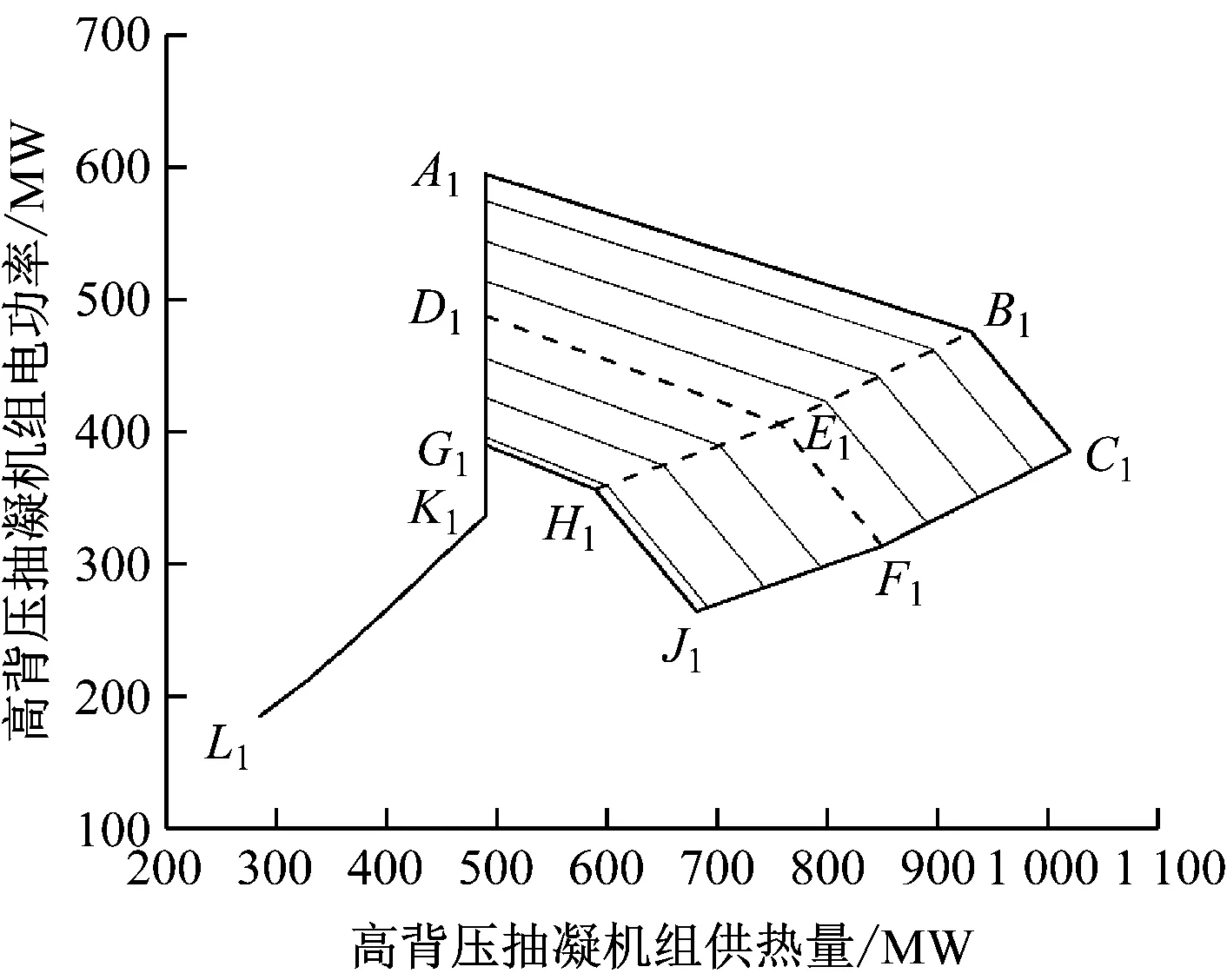
图3 高背压抽凝机组热电负荷可行域
通过将2台机组的热电负荷可行域进行矢量叠加,可得该双机热电联供系统总的热电负荷可行域如图4所示。由图4可知,系统热负荷可行区间为285.6~1 825.9 MW,电负荷可行区间为353.2~1 230.5 MW。根据高背压抽凝机组允许投入抽汽临界工况线,可将该系统可行域分成两部分:区域1中2台机组在给定热负荷的条件下均具备一定的调峰能力,是后续特性分析与负荷优化分配的基础;区域2中高背压抽凝机组仅投入乏汽供热,热电负荷一一对应,系统灵活度受到极大限制。
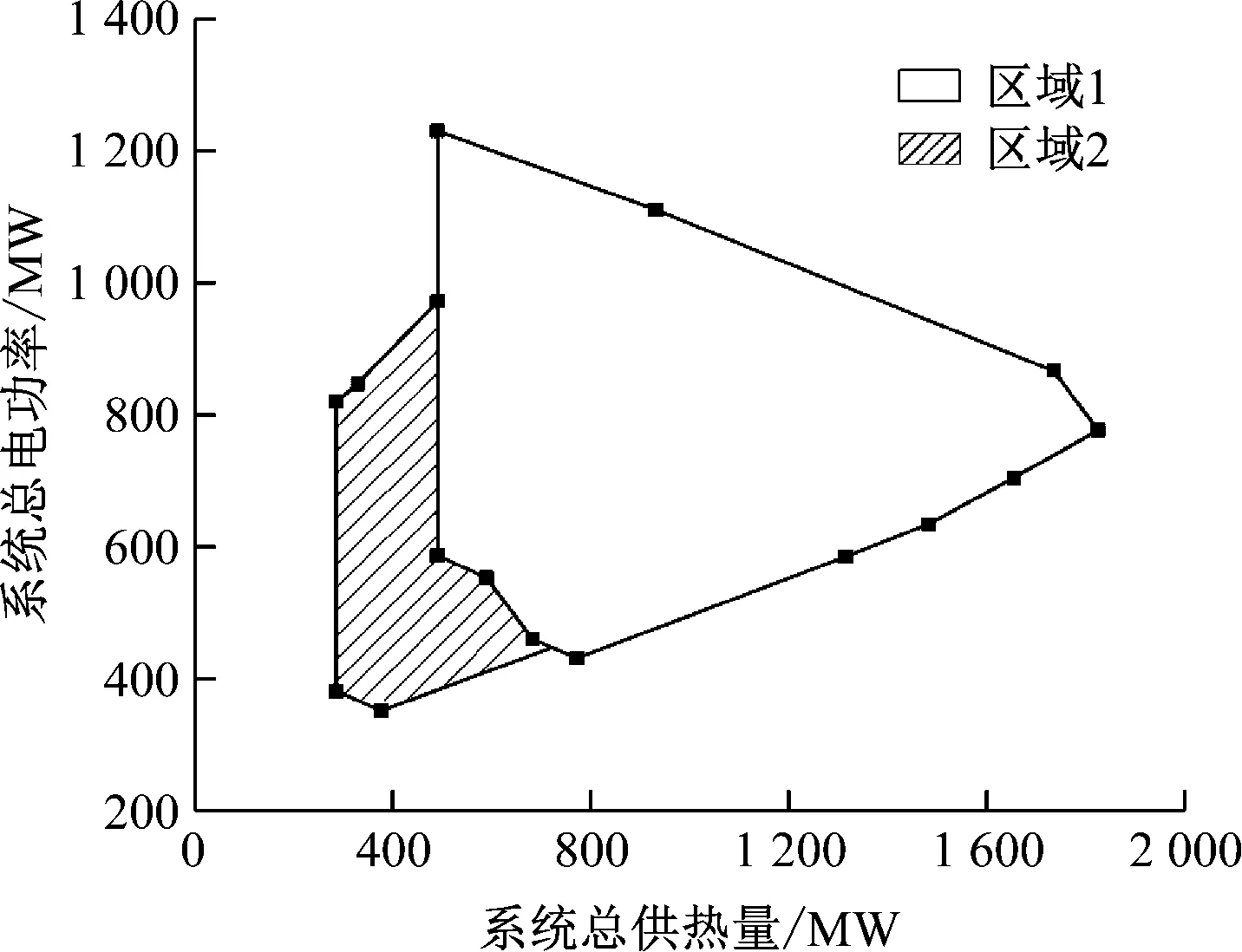
图4 系统热电负荷可行域Fig.4 Feasible range of thermoelectric load of the CHP system
3 改进的多目标灰狼算法
灰狼优化算法是一种新兴高效的群体智能优化算法,已成功应用于诸多领域[12]。该算法通过前三等级的狼群位置来更新种群,采用的更新机制收敛性和寻优效果均较好,然而其在相同的迭代次数下相比其他算法所需要的时间可能更长。考虑到热电负荷实时分配的问题,提出一种改进的多目标灰狼优化算法,以缩短负荷优化求解时间。
3.1 算法改进
该算法改进之处在于直接利用前三等级狼的位置和高斯采样完成进化过程,极大简化了种群更新机制。高斯采样过程如下:
(6)
式中:Xid(t+1)为个体i在第d维位置的随机变量,服从高斯分布,新位置xid(t+1)是Xid(t+1)的1个采样点;N(μ,σ2)为均值为μ,标准差为σ的高斯分布;μid为第i个灰狼第d维的高斯分布均值参数;σid为第i个灰狼第d维的高斯分布标准差参数。
μid=(αd+βd+δd)/3
(7)
σid=(|αd|+|βd|+|δd|)/c
(8)
式中:αd、βd、δd分别为前三等级狼第d维的位置;c为常数,根据实际情况选取。
为了平衡改进算法的搜索性能与收敛性能,针对标准差增加一个自适应系数m,进化过程表示为:
m=1.5-(iter/iter,max)
(9)
Xid(t+1)=μid+m·N(0,1)·σid
(10)
式中:iter为当前迭代次数;iter,max为最大迭代次数。
在迭代前期m较大,可以增加离搜索中心较远粒子的选择概率,增强算法的探索性能;在迭代后期m较小,可以加强算法的收敛性能。
3.2 求解流程
图5给出了MOGGWO算法的求解流程图,具体步骤如下:
步骤1,随机初始化灰狼种群的位置Xi(i=1,2,…,n),根据双目标适应度函数计算每个灰狼个体的适应度值,并对不满足约束条件的个体施加惩罚。
步骤2,计算初始种群中的非支配解集(大小固定),对非支配解集中的解进行网格计算,求各个个体的网格坐标值。
步骤3,从非支配解集中根据网格选择当前的最优解Xα、次优解Xβ和第三优解Xδ。
步骤4,根据式(7)和式(8)分别计算高斯分布的均值和标准差。
步骤5,利用高斯采样更新灰狼种群中灰狼个体的位置。
步骤6,根据适应度函数重新计算每个灰狼个体的适应度值,对不满足约束条件的个体施加惩罚。
步骤7,计算更新后灰狼种群的非支配解集,并将该解集与上次的非支配解集进行合并,获得新的非支配解集。
步骤8,对非支配解集中的解进行网格计算,求各个个体的网格坐标值。
步骤9,判断非支配解集是否超过预先设置的大小,若是,则根据网格坐标删除多余的非支配解。
步骤10,判断是否达到最大迭代次数,若是,则停止迭代并输出非支配解集;反之,转至步骤3。
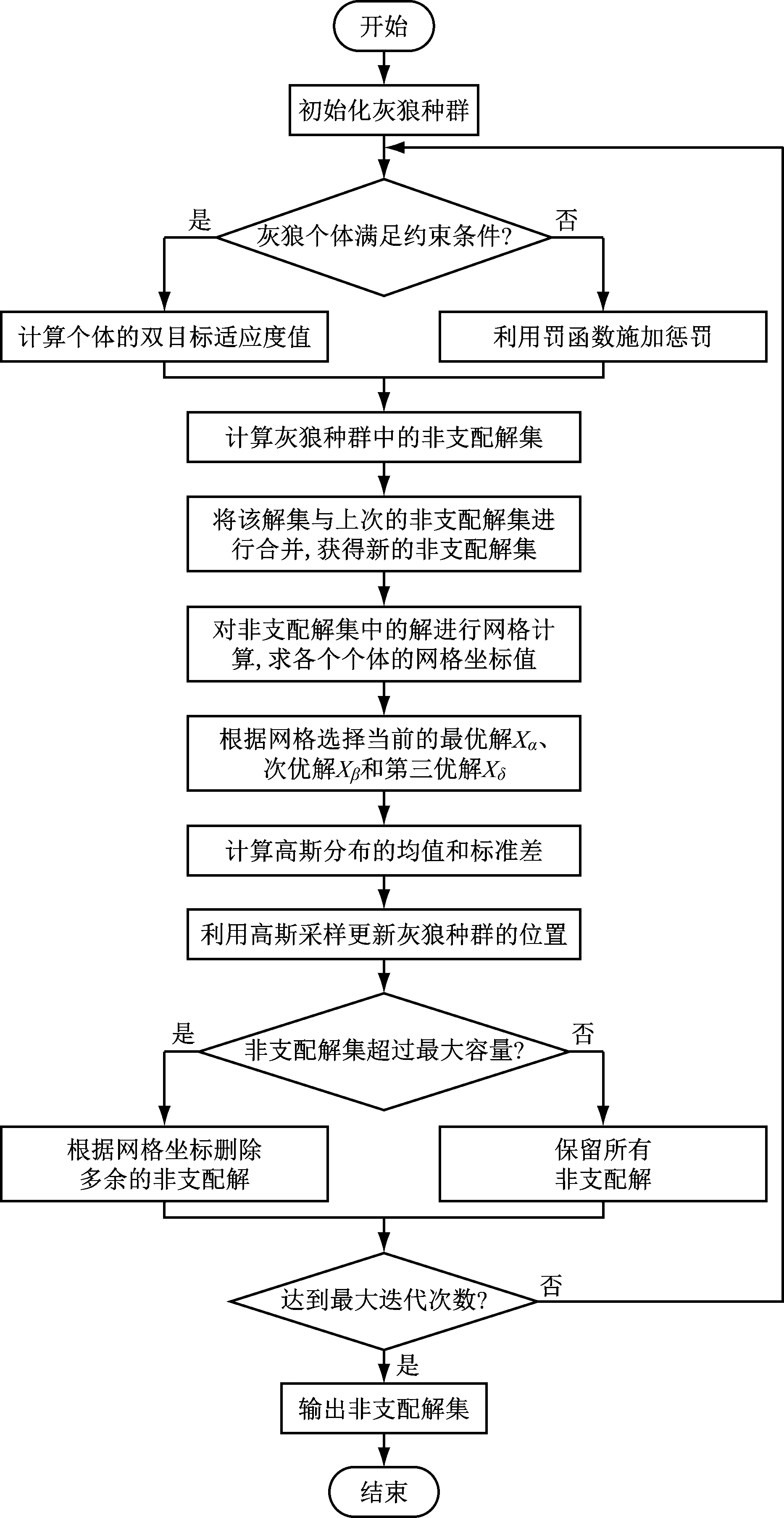
图5 MOGGWO算法流程图Fig.5 Algorithm flow of MOGGWO
4 结果与分析
4.1 热负荷分配对系统性能的影响
根据电网调度指令,保持高背压抽凝机组电负荷为300 MW、抽凝机组电负荷为400 MW不变,在给定系统总热负荷指令1 373 MW条件下,分析机组间热负荷转移对系统热耗及可再生能源消纳容量的影响。
图6给出了该典型工况下系统总热耗量及可再生能源消纳容量随抽凝机组供热量的变化。图中1号机表示高背压抽凝机组,2号机表示抽凝机组。由图6可知,在热负荷从高背压抽凝机组向抽凝机组转移的过程中,系统总热耗量呈先减小后缓慢增大的趋势,并在抽凝机组供热量为695 MW时达到极小值。这是因为当抽凝机组供热量小于695 MW时,高背压抽凝机组热耗减小速率大于抽凝机组热耗增大速率,当抽凝机组供热量大于695 MW时,高背压抽凝机组热耗减小速率略小于抽凝机组热耗增大速率。
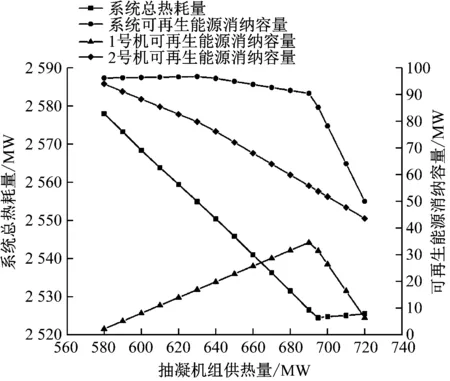
图6 系统总热耗量及可再生能源消纳容量随抽凝机组 供热量的变化
此外,从图6还可以看出,随着抽凝机组供热量的增大,高背压抽凝机组的可再生能源消纳容量呈先增大后减小的趋势,在抽凝机组供热量为690 MW时达到极大值,而抽凝机组的可再生能源消纳容量则呈逐渐减小的变化趋势,且在抽凝机组供热量大于630 MW时减小速率进一步加快。这是因为在抽凝机组供热量逐渐增大的过程中,其对应的最小电功率逐渐增大,高背压抽凝机组供热量逐渐减小的过程中,其对应的最小电功率呈先减小后增大的趋势。2台机组的可再生能源消纳容量叠加最终导致整个系统的可再生能源消纳容量呈先缓慢增大再缓慢减小随后迅速减小的变化趋势。
综上所述,在热负荷转移过程中,系统经济性和可再生能源消纳能力无法同时达到最优,可通过相应优化算法进一步探究多目标下的最优分配策略。
4.2 电负荷分配对系统性能的影响
保持高背压抽凝机组热负荷为803 MW、抽凝机组热负荷为570 MW不变,在给定系统总电负荷指令850 MW条件下,分析机组间电负荷转移对系统热耗及可再生能源消纳容量的影响。
图7给出了该典型工况下系统总热耗量及可再生能源消纳容量随高背压抽凝机组电功率的变化。由图7可知,在电负荷从抽凝机组向高背压抽凝机组转移的过程中,系统总热耗量呈先减小后增大的趋势,在高背压抽凝机组电功率为450 MW时减小速率有所减缓,且在电功率为490 MW时达到极小值。这是因为当高背压抽凝机组电功率小于490 MW时,抽凝机组热耗减小速率大于高背压抽凝机组热耗增大速率;当高背压抽凝机组电功率大于490 MW时,抽凝机组热耗减小速率小于高背压抽凝机组热耗增大速率。
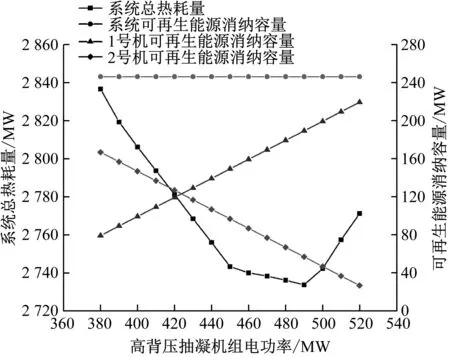
图7 系统总热耗量及可再生能源消纳容量随高背压抽凝 机组电功率的变化
此外,从图7还可以看出,随着高背压抽凝机组电功率的增大,高背压抽凝机组的可再生能源消纳容量呈递增趋势,而抽凝机组的可再生能源消纳容量则呈递减趋势。这是因为当各机组热负荷一定时,其所对应的机组最小电负荷也一定,因此各机组可再生能源消纳容量与其电负荷指令的变化趋势一致。2台机组的可再生能源消纳容量叠加最终导致整个系统的可再生能源消纳容量基本保持不变。
综上所述,在电负荷转移过程中,系统可再生能源消纳能力基本保持不变,此时应重点探究系统热耗最小时的负荷分配策略。
4.3 基于MOGGWO算法的热电负荷优化分配
根据各工况运行数据拟合得到高背压抽凝机组和抽凝机组热耗特性曲面,如图8和图9所示。
2台机组的热耗特性曲面表达式如式(11)所示,其中i=1,2,式中各项系数取值见表1。
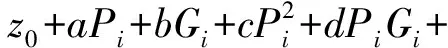
(11)
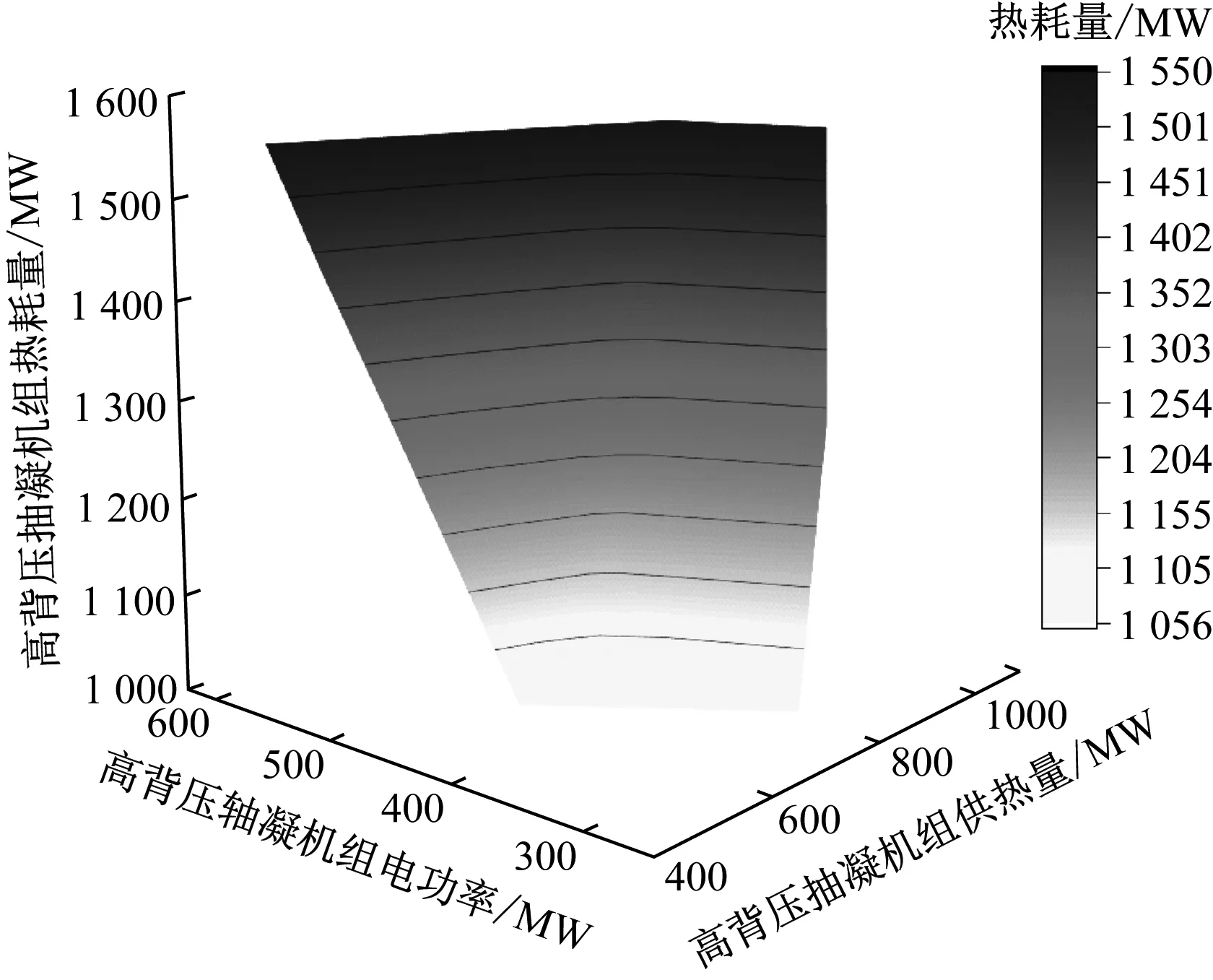
图8 高背压抽凝机组热耗特性曲面Fig.8 Fitting surface of heat consumption for high-back pressure unit with intermediate extraction
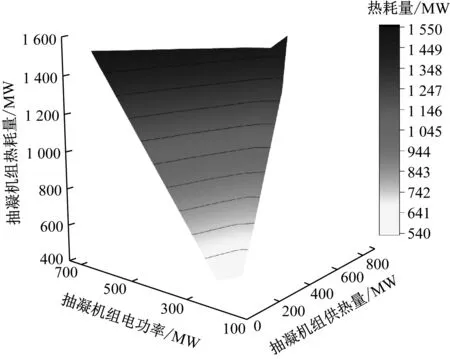
图9 抽凝机组热耗特性曲面Fig.9 Fitting surface of heat consumption for condensing unit with intermediate extraction
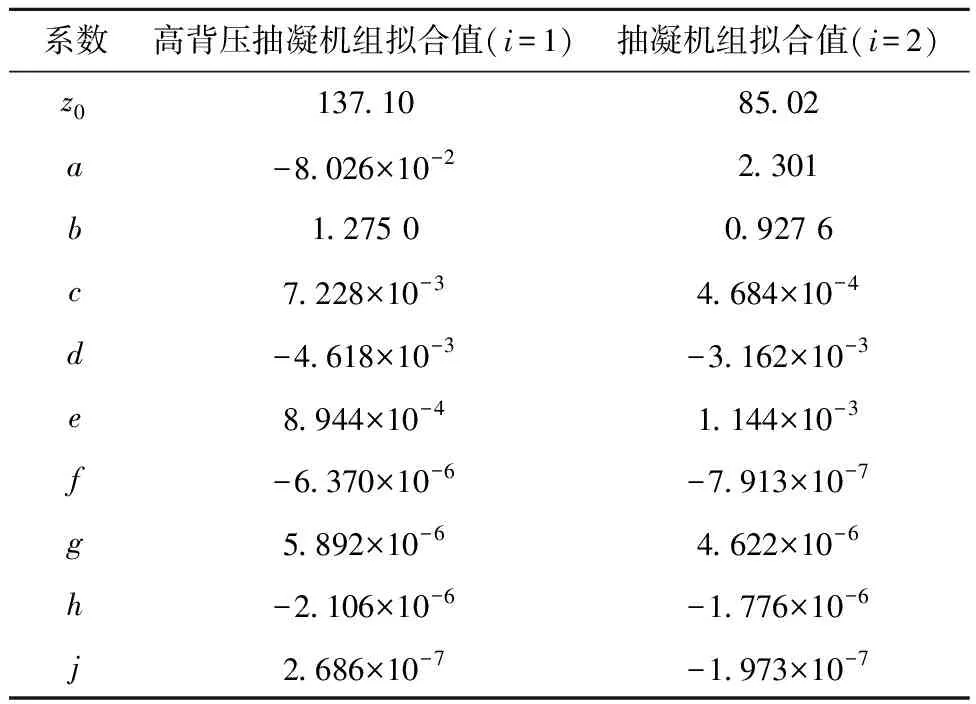
表1 各机组热耗特性曲面拟合系数Tab.1 Fitting coefficients of heat consumption surface ofeach unit
定义系统最小电功率函数Pmin,D(G1,G2) =Pmin,1(G1)+Pmin,2(G2),根据各工况运行数据拟合得系统最小电功率曲面如图10所示。
系统最小电功率函数表达式如式(12)所示,式中各项系数取值见表2。
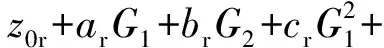
(12)
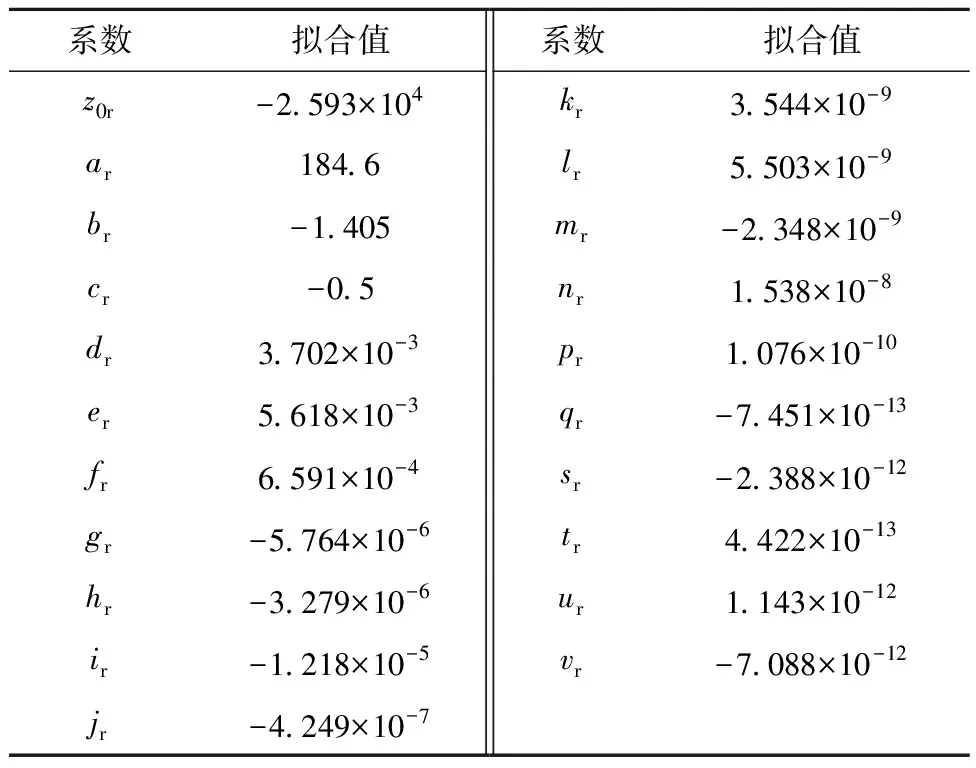
表2 系统最小电功率曲面拟合系数
将MOGGWO算法应用于所建立的多目标热电负荷优化分配模型中,种群数目设置为80,最大迭代次数为100。
图11给出了系统总电负荷指令为800 MW,总热负荷指令为1 200 MW时,通过该算法获得的帕累托前沿。由图11可知,当系统总热耗量降低5.02%时,系统可再生能源消纳容量相应降低6.53%,因此提高系统经济性的同时其可再生能源消纳能力将会降低,应根据现场实际情况权衡,进而选择热电负荷最优分配策略。
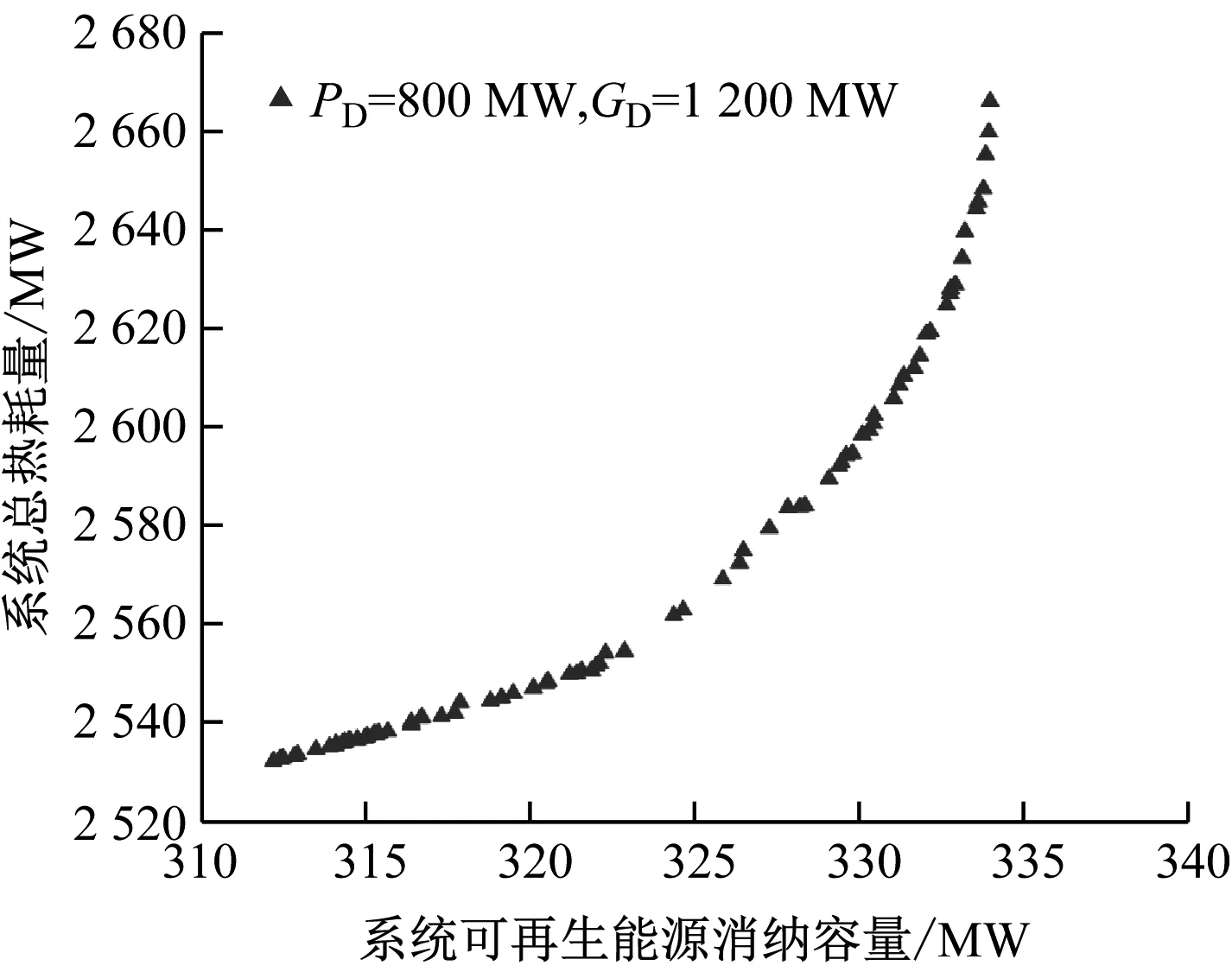
图11 多目标寻优结果Fig.11 Multi-objective optimization results
所提出的改进多目标灰狼算法极大地简化了种群更新机制,大大缩短了负荷分配求解的时间。在“双碳”大背景下,该算法能为大型热电联供系统的实时优化运行提出指导建议,有望获得可观的节能收益,具有未来工程应用的前景。
5 结 论
(1) 建立了600 MW双机热电联供系统的多目标热电负荷优化分配模型,其目标函数为系统总热耗量最小化及可再生能源消纳能力最大化,约束条件为各机组及系统的热电负荷可行域,结果表明,综合考虑中排压力限制、高背压供热机组允许投入抽汽限制和乏汽利用裕量边界后,机组可行域范围更准确,更具实际参考价值。
(2) 提出了一种基于高斯采样的改进多目标灰狼优化算法,该算法极大地简化了种群的更新机制,能大大缩短负荷分配求解的时间。
(3) 采用MOGGWO算法获得了多目标下的负荷优化分配解集,结果表明,提升系统经济性的同时其可再生能源消纳能力将会减弱,应根据现场实际情况权衡,进而选择热电负荷最优分配策略。
