基于双馈风电机组频率响应解析模型的系统低频减载策略

2023-11-20蔡国伟杨冬锋孙正龙刘晓军

电力系统自动化 2023年21期

姜超，蔡国伟，杨冬锋，刘铖，孙正龙，刘晓军

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学）,吉林省吉林市 132012）

0 引言

随着规模化风电机组经电力电子设备并网的发展,由同步机主导的传统电力系统逐渐转变为以新能源为主体的新型电力系统［1］。相对于传统同步系统,风电机组等新能源基本不提供惯量,导致新型电力系统遭受严重功率扰动后频率动态特性会恶化,严重威胁系统的安全稳定运行［2］。为提升新能源电力系统的频率特性,要求风电机组参与系统频率调节时［3］,虚拟惯量控制和一次调频辅助控制技术需要在一定程度上得到普及和推广［4-6］。

双馈风电机组作为主流应用的风力发电技术参与调频［7］,其复杂的控制环节增加了频率动态特性的分析难度。同时,对低频减载策略的影响也尚未厘清,现有研究对此考虑并不充分,忽略了双馈风电机组在频率紧急控制中的有益价值。

目前,国内外对双馈风电机组参与频率调节已开展了大量研究,主要集中在双馈风电机组频率控制策略和频率动态特性刻画方面。双馈风电机组参与系统调频通过调整换流器的控制策略实现,主要分为电流源型和电压源型。其中,电压源型换流器控制策略改造复杂、难以在实际中应用,本文不做重点讨论。电流源型换流器附加控制主要分为惯性控制、下垂控制、综合控制等。在此基础上,国内外专家学者提出了多种不同的控制策略,如基于减载系数变化的风电机组一次调频控制［7-8］、双馈风电机组变系数虚拟惯量优化控制［9］、抑制频率二次跌落的风电调频控制策略［10-11］、双馈风电机组自适应虚拟惯量控制［12-15］等。含双馈风电机组主动支撑的系统频率动态特性分析方面,主要研究集中在风电机组频率响应建模、虚拟惯量表征与估计、动态特性刻画等方面。文献［16］提出一种计及风电机组综合惯性控制的电力系统扩展频率响应模型。文献［17］建立了附加频率控制下双馈异步风电机组频率响应模型,并通过劳斯近似进行了模型降阶。文献［18］构建了惯量函数以分析双馈风电机组的动态惯性支撑作用。文献［19］基于幅相动力学提出了双馈风电机组惯性控制的小信号模型。然而,目前关于双馈风电机组参与调频的响应建模相对复杂,对低频减载的影响分析也不够充分。

低频减载问题是电力系统频率安全保护研究领域的重要课题,国内外学者对此开展了广泛的研究。传统低频减载策略采用分轮逐次逼近的切负荷决策方法,主要根据离线计算或工程经验,按照频率变化量分级切除预先设定的负荷［20］。传统方法难以适应系统运行方式的变化,容易造成过切、欠切等问题。而自适应低频减载方案通过计算系统受扰后的不平衡功率进而分配到各轮次进行切负荷操作［21-24］,能够定量考虑在线工况。除低频减载策略离线设计方法外,许多学者从优化角度开展了紧急切负荷的在线决策分析研究［25-27］,包括最佳切负荷位置和切负荷量的确定。然而,基于优化思想的紧急控制方案,严重依赖于优化模型的精度,当系统规模较大时可能难以满足保护的速动性要求。此外,人工智能的迅速发展致使其在电力系统紧急控制领域得到了初步应用［28-29］。但是,新能源电力系统组合爆炸式运行场景和高维复杂不确定性对人工智能训练数据提出了更高的要求。尽管目前的低频减载策略研究已经十分丰富,离线设计的低频减载方案由于其工作原理清晰、操作简单,仍作为目前国内外电网频率安全紧急控制的主流措施［30］。但是,现有研究对风电机组辅助控制的影响考虑并不充分,仅有少数学者对该问题进行了初步研究。文献［31］分析了双馈风电机组惯性控制和一次调频辅助控制对低频减载的影响。文献［32］考虑风电机组惯性控制和低频保护,动态整定功率缺额。

综上,针对目前新能源电力系统低频减载策略设计的不足。本文推导了双馈风电机组综合惯量控制的频率响应线性化解析模型,揭示了双馈风电机组辅助控制策略能够提升系统频率特性的根本原因,并厘清双馈风电机组辅助控制对低频减载的增益影响,从而提出了规模化双馈风电机组参与调频的低频减载策略。

1 双馈风电机组频率响应解析模型构建

目前,大部分双馈风电机组通过锁相环跟网运行,主要通过在功率外环上附加额外控制环节参与系统频率调节,利用风电机组转子中储存的动能和减载运行提供的备用容量为系统频率提供支撑。为更好地理解含规模化双馈风电机组电力系统的频率响应特性,需要厘清和解析双馈风电机组参与频率调节的动态过程。

1.1 双馈风电机组空气动力学模型

风电机组捕捉风能并将其转化为机械能,进而为发电机提供动力产生电能。双馈风电机组在给定风速下产生的可用机械功率Pm可表示为:

式中:ρ、R和V分别为空气密度、风电机组转子叶片半径和风速；Cp为风电机组的功率系数,是风电机组桨距角β和叶尖速比λ的非线性函数,见式（2）。

式中:c1、c2、c3、c4、c5、c6为相关系数；wr为风电机组的转速；λi为过程量,没有物理意义。

不同风速下的双馈风电机组的机械功率曲线如附录A 图A1 所示,可以看出不同风速下均存在最大的功率捕捉点。为了最大化利用风能,一般情况下要求双馈风电机组实现最大功率点跟踪（MPPT）运行。将式（3）代入式（1）,可将风电机组机械功率Pm重新整理为:

通过调节风电机组转速,在给定风速下使双馈风电机组达到最佳的功率系数C,进而使双馈风电机组捕获最大的机械功率P［33］:

式中:λopt为最佳的叶尖速比；kopt为最佳功率跟踪函数系数。

根据式（6）可知,双馈风电机组的MPPT 曲线为三次方函数,如附录A 图A1 所示。为使双馈风电机组在参与频率调节时提供备用容量,要求风电机组减载运行。由式（1）可知,假设风电机组以减载率σ运行,只需风电机组的运行功率系数C=(1-σ)C即可,求得减载运行的风电机组叶尖速比λde,并令ε=λde/λopt。因此,减载运行的风电机组机械功率P可以表示为:

式中:kde为减载功率跟踪函数系数。

由式（7）可知,双馈风电机组减载运行曲线仍为三次方函数,见附录A 图A1。需要说明的是,风速达到及超过风电机组额定值的运行工况只占很小一部分［34］。因此,基于MPPT 运行转速区间实施超速减载获取备用容量在大部分时间内相对适用［35］。

1.2 双馈风电机组综合惯量控制频率响应模型构建

双馈风电机组综合惯量控制将系统频率导数和偏差信号附加到功率外环参考值上,从而实现系统频率和风电机组转速耦合。分析双馈风电机组的频率响应过程,需对其异步发电机数学模型和功率控制环节进行简化。附录A 图A2 所示为双馈风电机组典型的转子侧逆变器控制环节的示意图,主要包括功率外环、电流内环、Park 变换和脉宽调制,此外,双馈风电机组的有功和无功控制一般是解耦的。

假设转子和定子为三相正弦对称,基于旋转场和Park 变换经典理论,在dq参考坐标系下风电机组的转子和定子电压方程可以定义为［36］:

式中:Vds、Vqs和Vdr、Vqr分别为dq参考坐标系下的定子和转子电压；ids、iqs和idr、iqr分别为dq参考坐标系下的定子和转子电流；Rs和Rr分别为定子和转子电阻；Xs和Xr分别为定子和转子电抗；Xm为定子绕组和转子绕组间的互抗。

需要特殊说明的是,式（8）已经忽略了定子和转子绕组的暂态过程。dq参考坐标系下双馈风电机组转子和定子的磁链方程为:

式中:φds、φqs和φdr、φqr分别为dq参考坐标系下定子和转子侧磁链。

进而双馈风电机组的电磁转矩Te可表示为:

定子磁链定向矢量控制是目前应用最广泛的双馈风电机组转矩/功率控制策略。将d轴定位于发电机定子磁链的方向,使其与定子磁链的最大值重合,由于定子直接与网侧连接,定子磁通和电压可视为常数［37］,即

式中:φs为定子磁链的幅值；ws为同步转速；Vs为定子电压的幅值。

将式（11）和式（12）代入式（8）、式（9）和式（10）,定子电压方程可重新推导为:

电磁转矩可进一步推导为:

由式（13）可知,d轴或者q轴的转子电流并不完全独立于d轴或者q轴的转子电压,这意味着双馈风电机组的有功和无功控制是相互耦合的。根据式（13）和式（14）可知,双馈风电机组侧逆变器的有功控制详细环节如附录A 图A3 所示。为实现双馈风电机组的有功和无功解耦控制,一般会在电流外环的输出端叠加补偿项,经化简,可得到更为简化的有功控制环节,如附录A 图A4 所示。然而,图A4 所示控制环节为电磁控制,缺少对风电机组转速控制环节的考虑,且为开环控制。双馈风电机组的电磁输出功率Pe由定子侧功率输出和转子侧功率输出组成,可表示为:

忽略双馈风电机组的阻尼系数,其转子运动方程可表示为:

式中:HDFIG为风电机组转子的惯性时间常数；Tm为风电机组转子的机械转矩。

根据附录A 图A1 可以看出,给定风速下和一定的转速区间内,风电机组的机械功率和机械转矩可近似拟合为转速的多项式函数［38］。通过最小二乘法可将Tm表示为:

式中:a、b、c、d、e、f为多项式的相关系数。

附录A 图A5 所示为10 m/s 风速下的功率和转矩多项式拟合值和真实值的对比曲线,可以清晰地看出,当转速超过0.4 p.u.时,拟合方法的精度很高,且一般来讲,风电机组的转速超过0.5 p.u.时才能发电。因此,本文所提拟合方法满足工程要求。

将式（7）、式（14）、式（15）和式（16）嵌入附录A图A4,可得出完整的双馈风电机组有功响应环节,如图1 所示。图中:ΔP为与系统频率相关的附加功率信号；PI 表示比例-积分环节；Pref为给定功率参考值；Iqr和Iqr,ref分别为转子侧q轴电流幅值及其参考值；Iqs为定子侧q轴电流幅值；s为拉普拉斯算子；f(u)为式（17）所示函数,其中u为自变量。然而,图1 所示为非线性控制环节,难以继续分析风电机组的频率响应特性。将式（15）展开可得:

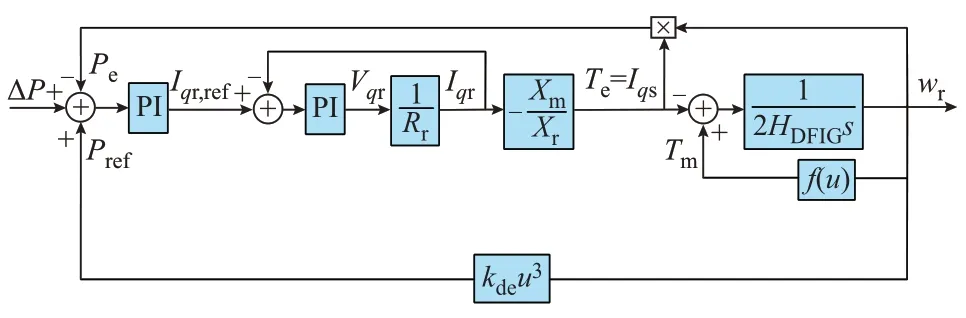
图1 转子逆变器完整有功功率控制Fig.1 Complete active power control of rotor converter

式中:下标0 表示对应变量的初值；Δ 表示对应变量的变化量。

忽略式（18）的高阶项［26］,双馈风电机组的电磁功率增量ΔPe可表示为:

根据式（17）,可将图1 所示的控制环节线性化,如图2 所示,机械转矩增量ΔTm的具体表达式见式（20）。

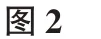
图2 转子逆变器有功控制小信号模型Fig.2 Small-signal model of active power control of rotor converter

至此,双馈风电机组频率综合惯量控制的线性化模型建立完毕。

2 双馈风电机组调频特性对低频减载的影响分析

本章将从双馈风电机组惯性控制及一次调频控制频率响应模型的推导入手,分析风电机组频率支撑作用的本质,进而厘清风电机组参与调频对低频减载的影响。

2.1 惯量模拟的双馈风电机组功频传递函数推导

假定双馈风电机组仅以惯量模拟的形式参与系统频率影响,即风电机组仍在MPPT 运行,利用转子中蕴藏的动能为系统提供频率支撑。类比图2,双馈风电机组惯量模拟的线性表达式可表示为:

把式（22）—式（27）代入式（21）,可得双馈风电机组频率响应的传递函数Gin(s),具体推导见附录B。

根据式（28）可以清晰地看出,风电机组的频率响应传递函数表示的是风电机组的有功功率增量与系统频率偏差的关系,风电机组参与频率响应实际上改变了系统的电磁功率。

2.2 综合惯量模拟的双馈风电机组功频传递函数推导

双馈风电机组综合惯量频率响应（惯量模拟和一次调频）利用转子中包含的动能和备用容量为系统提供频率支撑。根据图2,除去式（20）—式（25）,双馈风电机组模型的表达式可表示为:

式中:kp为风电机组下垂控制比例系数。

进而,双馈风电机组频率响应的传递函数Gde(s)如式（46）所示,具体推导见附录C。

2.3 双馈风电机组频率辅助控制对减载切负荷量的影响分析

基于2.1 节和2.2 节的双馈风电机组研究结果,包含风电机组频率辅助控制和低频减载的电力系统频率响应模型如图3 所示。图中:ΔPshort为系统功率缺额；ΔPshed为低频减载的负荷切除量；GWF(s)为双馈风电机组功频传递函数；D为系统阻尼系数；ΔPWF为风电机组输出功率增量。

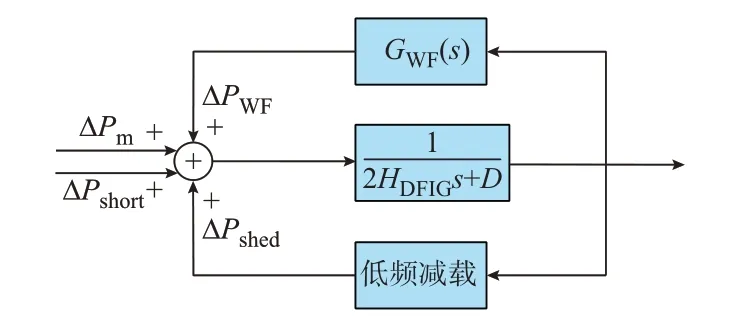
图3 含风电支撑和低频减载的系统频率响应模型Fig.3 System frequency response model with wind power support and under-frequency load shedding

假设GWF(s)=Gin(s),即双馈风电机组仅通过惯量模拟来实现对网侧频率的支撑。根据图3,功率缺额与频率的数学关系s域表达式可推导为:

式中:R为调速器调节系数；Ggov(s)为同步机调速器的传递函数,如式（58）所示。

式中:TG为调速器时间常数；TRH为再热蒸汽容积时间常数；FHP为汽轮机高压缸做功比例；TCH为蒸汽容积时间常数。

将式（28）和式（58）代入式（57）,可以得到:

一般情况下,ΔPshort设置为阶跃函数形式,即

式中:ΔPstep为功率缺额的幅值。

将式（61）代入式（57）可得:

根据初值定理,系统初始频率变化率可表示为:

根据终值定理,系统准稳态频率偏差和双馈风电机组稳态功率支撑可表示为:

可见,系统初始频率变化率和准稳态频率偏差不受双馈风电机组惯性模拟控制策略的影响,稳态时并不体现功率支撑,即双馈风电机组惯性控制难以弥补系统低频减载的切负荷决策量。

假设GWF(s)=Gde(s),即双馈风电机组减载运行并通过惯性模拟和一次调频控制提供频率支撑。类比式（57）—式（62）,系统初始频率变化率、系统准稳态频率偏差和双馈风电机组稳态功率支撑可表示为:

由式（66）—式（68）可见,系统初始频率变化率依然与双馈风电机组频率辅助控制无关。然而,系统准稳态频率偏差却受双馈风电机组影响,与双馈风电机组的初始运行状态、控制器参数以及发电机参数密切相关。同样,稳态时双馈风电机组的支撑功率也和以上参数密切相关。即双馈风电机组减载运行时频率辅助控制可弥补部分低频减载的切负荷决策量。

值得注意的是,控制参数设计适当,双馈风电机组解析模型量化风电机组综合惯量响应下的动态和稳态特性是可行的,因为风电机组转速并不会发生过大变化。附录D 图D1 所示为不同风电机组控制参数下的转速轨迹,显然风电机组转速偏差并不大。

3 双馈风电机组参与调频的电力系统减载策略

3.1 考虑双馈风电机组调频的低频减载切负荷量决策

低频减载能够有效阻止系统发生频率崩溃。当系统发生严重的功率缺额事件后,频率快速下降至触发阈值,低频减载将会启动分批切除负荷。因此,负荷切除量的确定是低频减载的关键问题。结合2.3 节的研究结论,给出系统频率紧急控制的负荷切除量求解过程。

假设系统在初始时刻,即t=0 时,系统发生大规模功率缺额ΔPshort,根据2.3 节结论,双馈风电机组对系统初始频率变化率没有影响,可得到ΔP的表达式为［30,39］:

需要注意的是,实际电网中,最大频率变化率难以测量,一般关注扰动后一段时间内的平均频率变化率,典型的时段长度如200 ms 或500 ms［39］。设电力系统频率紧急控制后要求达到的稳态频率值不低于wt,即要求稳态频率偏差低于Δwt=1-wt。考虑低频减载动作,结合2.3 节的结论,稳态时系统功率缺额组成可表达为:

式中:ΔPL为稳态时负荷调节功率。

根据终值定理,式（69）可进一步推导为:

因此,在保证准稳态频率偏差不高于Δwt的条件下,低频减载切负荷总量可计算为:

3.2 低频减载策略实施方案研究

1）低频减载轮次、动作阈值及各轮切除量的确定

在频率紧急控制过程中,为充分利用系统的旋转备用容量和抽水蓄能机组的调节能力,大电网的频率值一般不宜超过49.25 Hz,动作频率级差范围一般设置为0.2 Hz,基本轮次可设置为3～8 轮［30］。根据实际电网情况,本文设置减载轮数为3 轮,动作频率阈值分别设定为49.2、49.0、48.8 Hz,最大动作延时设置为0.2 s,各轮次的减载比例分别设定为功率缺额的20%、25% 和55%,同时设置dΔw/dt超过1 Hz/s 加速启动下一轮减载动作。考虑到系统可能出现小扰动的情况,导致基本轮不能全部启动,使得系统频率悬停在稳态恢复频率值wt下方。因此,另设置一级特殊轮,动作延时15 s,减载量为剩余基本轮的可切负荷量。

2）低频减载地点及功率分配

低频减载的实际实施过程中,需对系统中分布的节点负荷进行切除。通过分析减载地点和减载量对系统频率变化的灵敏度［40］,选择减载位置和确定切负荷功率。采用文献［40］提出的方法,可确定电网中不同节点的切负荷量,即

式中:ΔPshed,j为节点j负荷切除量；为负荷节点j的灵敏度,与负荷节点到扰动节点的电气距离直接相关；Ld为负荷节点的集合。

3）低频减载执行策略设计

基于前述分析,本文按照附录D 图D2 所示低频减载策略进行频率紧急控制:（1）首先,设置低频减载各轮次动作频率阈值wi、减载比例ζi以及稳态恢复频率值wt；（2）根据预先设定的wt,按照式（72）计算低频减载量；（3）检测系统频率状态,如频率变化率dΔw/dt<0 且频率值w≤w1,则启动低频减载装置。如完成第i轮减载后,系统受小扰动影响导致频率悬浮于稳态设定值下方,但却未达到下一轮频率动作阈值,则启动特殊轮。

4 算例分析

在MATLAB/Simulink 平台中构建附录D 图D3 所示IEEE 39 节点系统,验证本文所提策略和方法的有效性和优越性。图D3 中,将节点32、34、35以及37 处的同步机组替换为双馈风电场,风电渗透率约为42%,风电场由双馈风电机组等值聚合构成,双馈风电机组的详细参数见附录D 表D1,同步机组、线路及负荷等参数参考文献［41］。

4.1 双馈风电机组频率解析模型准确性验证

为验证本文所提风电频率响应解析模型的准确性,以附录D 图D3 所示系统为例,设置节点32、34和35 处的风电场不参与系统调频,仍采用MPPT 控制,节点37 处风电场仅采用惯性控制,并在t=10 s时,设置节点16 处增加300 MW 的负荷。结合前文所述的风电机组解析模型,构建改进的IEEE 39 节点系统频率响应模型,见附录D 图D4。同时,选取距离风电场W8 较近的同步机组G1、G9 和G10 的频率作为对比,以验证本文所提风电模型的有效性。

图4 所示为时域仿真和频率解析模型的对比结果。从图中可以看出,在受到扰动后几秒钟,惯性控制的双馈风电机组能够为系统提供短暂的功率支撑,可以提升系统频率的动态特性。此外,从图中也可清晰地看出,对比时域仿真结果,所提频率解析模型能够准确地刻画系统的频率轨迹和双馈风电机组功率输出,且双馈风电机组稳态输出功率增量为0,这直接证明了所提双馈风电机组解析模型及其分析的准确性。

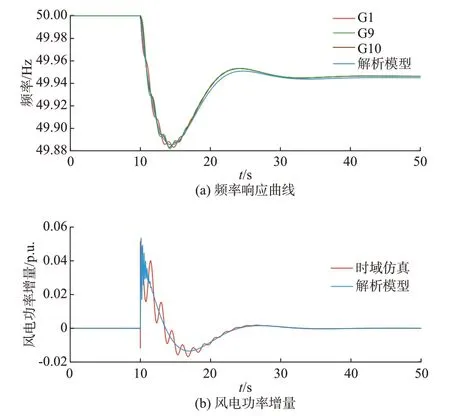
图4 惯性控制下解析模型和时域仿真的对比Fig.4 Comparison of analytical model and timedomain simulation with inertia control

同样,设置节点37 处风电场采用惯性控制和一次调频控制,图5 所示为时域仿真和频率解析模型的对比结果。相对于惯性控制,一次调频控制能够进一步改善系统频率特性,频率最低点和稳态频率偏差两个指标均得到明显提升,同时,双馈风电机组稳态功率输出也发生明显变化,且频率动态过程中没有发生超调现象。

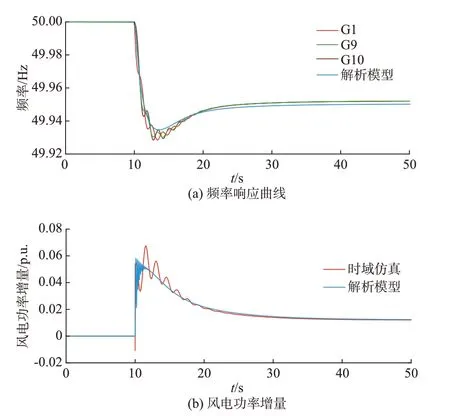
图5 一次调频控制下解析模型和时域仿真的对比Fig.5 Comparison of analytical model and time-domain simulation with primary frequency regulation control

为验证风电惯量响应的本质为对系统电磁功率的主动支撑,搭建了如附录D 图D5 所示的双机测试系统。在t=10 s 时,设置节点3 突增50 MW 有功负荷,同步机组具体参数见附录D 表D2。附录D 图D6 所示分别为双馈风电机组在MPPT 运行模式和惯量响应控制下系统同步机机端电磁功率时域曲线,可见,风电机组的惯量控制会深刻影响同步机组机端电磁功率动态变化。双馈风电机组影响频率的过程可解释为如下物理过程:系统中功率扰动导致同步机组电磁功率变化；其次,导致机组转速变化,进而引发风电机组所在节点频率的变化,再次在控制作用下改变机端输出功率,从而影响同步机组电磁功率来影响系统频率。

4.2 双馈风电机组辅助频率控制对低频减载的影响分析

为分析风电机组辅助频率控制对系统低频减载的影响,以t=10 s 时节点38 处同步机组G9 故障切机（机组稳态发电功率为920 MW）模拟系统大功率缺额扰动,设置稳态频率不低于49.5 Hz,通过图3所示频率响应模型实施低频减载方案,并设置4 种工况来验证分析本文所提策略的有效性。

工况1:双馈风电机组不参与系统频率调节,通过式（69）计算系统切负荷量。

工况2:双馈风电机组不参与系统频率调节,考虑调速器稳态功率支撑计算切负荷量。

工况3:双馈风电机组通过惯性控制参加系统的频率调节,考虑调速器稳态功率支撑计算切负荷量。

工况4:双馈风电机组通过惯性控制和一次调频控制参加系统的频率调节,通过式（72）计算切负荷量。

图6 为4 种工况下低频减载后系统的频率轨迹,附录D 表D3 所示为减载的具体措施,可见,应用不同的减载策略,系统频率响应特性差异性较大。

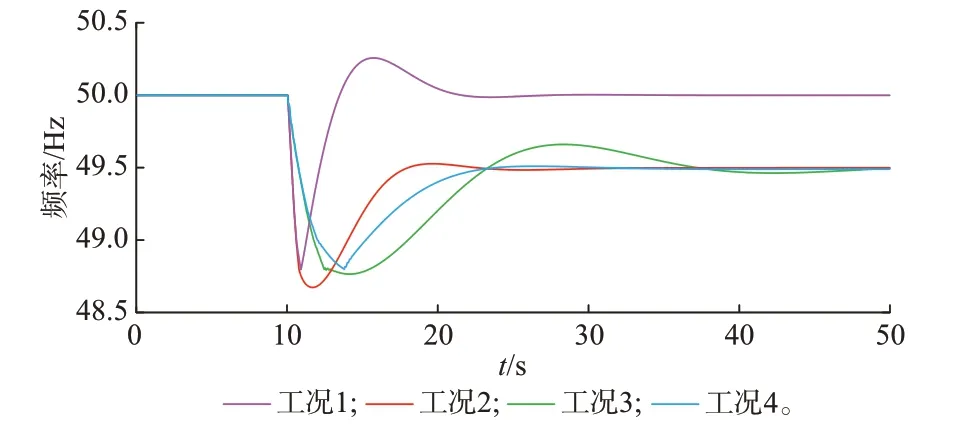
图6 不同工况下系统低频减载频率响应轨迹Fig.6 System frequency response trajectories of under-frequency load shedding under different working conditions

工况1 下,减载量设定为系统受扰后功率缺额,不考虑调速器的稳态补偿功率。系统频率最低点较高,且到达频率最低点时间最短,约10 s 系统频率暂态过程结束,稳态频率偏差为0,但是在频率恢复中出现明显超调现象,且系统减载功率为4 种工况下最高。

工况2 下,系统减载量计及了调速器的稳态功率补偿,切负荷量相较于工况1 减少了368 MW,但是系统频率最低点却是4 种工况下最低的,达到了48.67 Hz。

工况3 下,系统双馈风电机组通过惯性控制参与系统调频,风电惯性控制对系统稳态频率偏差没有影响,所以减载量和工况2 一致,但是风电机组惯性控制对系统频率动态特性影响显著,相较于工况1 和2,工况3 下受扰后系统频率变化率明显降低,但频率恢复过程时间在4 种工况中最长。

工况4 下,系统双馈风电机组通过惯性控制和一次调频参与系统调频,风电一次调频控制对系统稳态频率偏差产生影响,能够进一步补偿部分稳态功率缺额,所以减载量相较工况2 和3 进一步减小,为515.2 MW。同时,相比其他3 种工况,工况4 下系统频率变化率和频率最低点两个频率动态指标都得到明显的改善。需特别指出的是,系统频率动态过程中并未发生超调现象,且稳态频率恢复也较快。

为进一步证明所提低频减载策略的有效性和优越性,在与4.1 节相同故障工况的算例背景下,本文给出了文献［31］、文献［32］和本文所提减载策略的对比结果,如附录D 表D4 所示。从表D4 中可以看出,3 种减载策略的频率最低点差异不大,这是因为调频过程中3 种策略均考虑了风电机组的惯量支撑作用,然而文献［32］所提减载策略由于忽略了调速器的作用导致加载总量相对较大；文献［31］所提策略考虑了系统的等效惯量降低了减载总量,但是稳态频率却有可能降至49.5 Hz 以下,这是因为风电机组的惯量控制在稳态时不体现功率支撑,在频率调节的中后期,风电机组会吸收电网功率来完成转速恢复。

4.3 风速条件对低频减载的影响分析

由2.3 节可知,双馈风电机组综合惯量控制下稳态支撑功率和风速条件强相关。附录D 图D7 所示为不同风速下双馈风电机组参与调频系统低频减载量对比结果。不难看出,随着风速的上升,系统低频减载量不断下降。原因如下:根据附录A 图A1可知,双馈风电机组MPPT 点和减载功率点均随风速的提升呈三次方增加,导致风电机组减载运行工况下,备用容量随风速上升而不断提高,进而抵消了更多的低频减载量。