含限流电抗器的环形直流微电网暂态对地高频电压保护方法

2023-11-20霍锐成黄文焘余墨多邰能灵

电力系统自动化 2023年21期

霍锐成，黄文焘，余墨多，邰能灵，姚刚，王云

（1.上海交通大学电子信息与电气工程学院,上海市 200240；2.南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省南京市 211106；3.智能电网保护和运行控制国家重点实验室,江苏省南京市 211106；4.国网上海市电力公司,上海市200122）

0 引言

直流微电网技术对推进节能减排和实现能源可持续发展具有重要意义,在未来智能配用电系统尤其是分布式能源供应的系统发展中,占据了重要地位［1-3］。直流微电网的主要挑战之一是缺乏有效的保护解决方案［4］。直流微电网相较于直流配电网线路更短、阻抗更低,且分布式电源和负荷的投切增加了保护方案整定与判别的难度,因此,用于直流配电网、高压直流电网中的常规保护方案将不再适用［5］。快速检测和消除故障电流是直流微电网的主要挑战［6］,利用暂态信息快速、有选择地切除故障是有效的解决方案,已有许多学者对直流微电网的暂态保护进行了研究。考虑到直流微电网故障响应迅速,文献［7］指出快速、有效的保护方案是直流微电网发展的基础,并对直流微电网的故障暂态模型进行了详细分析；文献［5］提出一种利用振荡频率和振荡第1 周期的相关瞬态功率来保护直流微电网的方法；文献［8］利用母线两侧暂态功率变化率作为差动量,构成保护判据。

与直流输电网、直流配电网相类似,为避免在直流故障检测期间损坏电力电子设备,直流微电网在线路上需安装限流电抗器,以抑制故障电流上升率［9-10］,也相应地为直流微电网提供了边界条件。故障后线路边界具有较为丰富的暂态特征,国内外学者对此进行了研究,主要可分为单端边界保护和双端边界保护［11］。

对于单端边界保护,文献［12］提出可利用限流电抗器电压的变化率检测网状多端系统中的直流故障,但其仅考虑了两极故障。文献［13］设计了线路电压变化率保护判据,但该方案受到限流电抗器取值的影响。文献［14］利用限流电抗器暂态电压能量来识别内部故障和正向外部故障,并通过电压幅值比来判断故障方向,但该方法考虑了行波［15］,不适用于线路较短的直流微电网。

对于双端边界保护,文献［16］利用暂态能量差构成保护判据。文献［17］将原本的限流电抗器边界扩大,并通过扩大后边界的暂态能量进行故障判断,该方案对数据同步有一定的要求。文献［18］利用限流电抗器故障区内外电压的不同构成保护判据,能够实现故障选线和选极,但面对较高故障电阻时,可能会出现误动的情况。文献［19］利用故障后限流电抗器出口与换流器出口电压比构成保护判据,提出了单端与双端保护配合的判据实现保护速动性和选择性,但该方案对采样频率要求较高。

针对现有单端边界保护难以判断线路末端故障和双端边界保护要求采样频率较高、速动性相对不足等问题,本文所提出的保护方案利用故障后线路两侧限流电抗器暂态高频电压模值的大小关系作为保护判据,保护易整定且无须上、下级线路配合。通过选择合适的频率解决了线路背侧阻抗呈容性导致保护拒动问题,对通信要求较低,可以较快识别且定位直流故障区域,且能够避免新能源接入电网时产生的影响。仿真实验表明,该方法在不同故障类型、运行方式以及较高过渡电阻下,均能够快速检测并有选择性地切除故障。

1 直流微电网结构与故障特性

1.1 直流微电网结构

直流微电网具有放射形、环形等结构［20-21］。放射形直流微电网结构简单、建设成本较低,且在线路电能的传输过程中相互解耦,在研究线路故障和保护方案时线路单独考虑即可。环网中的电源可对负荷进行双向供电,故该结构增加了系统的可靠性及故障或设备检修期间运行的灵活性,但又因为环形结构包含故障和任何节点之间的两条路径,环网在线路电能的传输过程中相互耦合,在研究线路故障和保护方案时需要考虑上、下级保护的配合。因此,放射形电网的保护方案在环网中常常不适用,环网的故障识别更为困难［22］。为此,本文针对环形直流微电网的保护方案进行了研究。

五端环形直流微电网拓扑结构如图1 所示。五端结构由多类型换流器、直流线路和变压器等连接风机、光伏、直流负荷、储能和交流系统组成。接地方式为直流侧经分裂电容中点直接接地。本文以两极故障为例,单极接地故障可按照同样的方法分析。

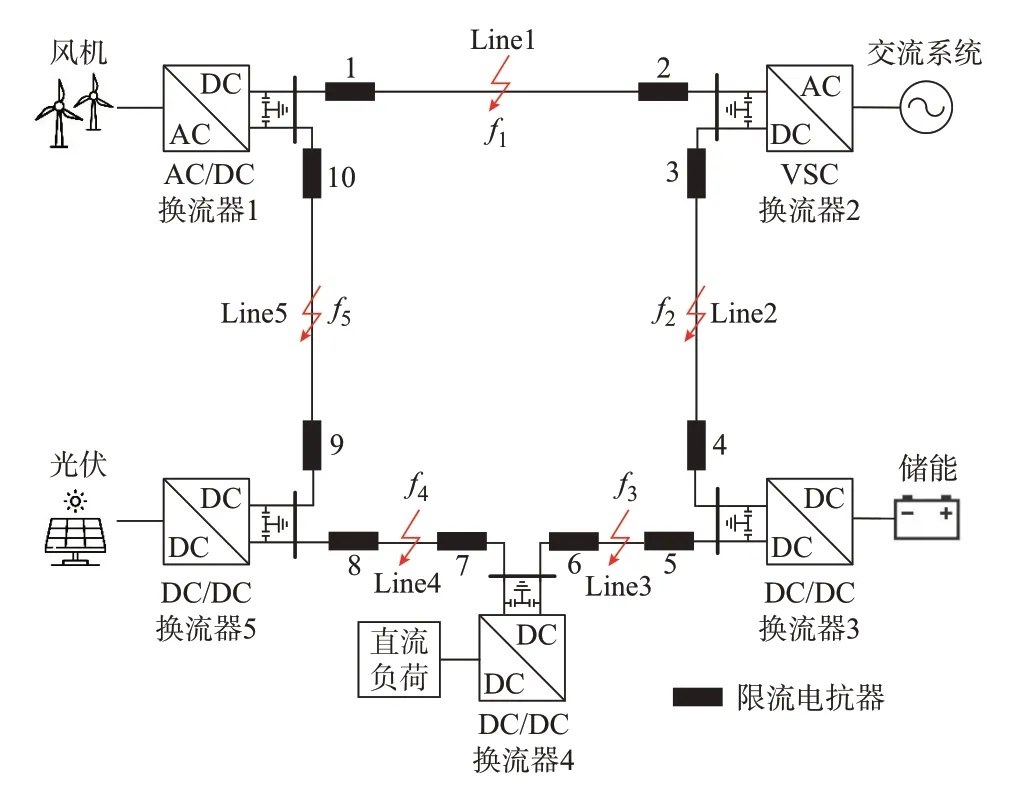
图1 五端环形直流微电网拓扑结构Fig.1 Topology of five-terminal ring DC microgrid

1.2 故障特性分析

在系统发生线路故障时,对于电压源换流器（voltage source converter,VSC）端口故障暂态过程可分为3 个阶段［23］:直流电容放电阶段、二极管自然换向导通阶段、二极管同时导通阶段,本文主要讨论直流电容放电阶段。对于AC/DC 和DC/DC 端口,在故障时可同样将其等效为电容并联在线路一侧［24］。

系统发生短路故障后,短路点处电压出现类似于阶跃信号的波形,会瞬间跌落到一定值［25］,利用傅里叶变换可以发现该信号含有各个频率的谐波分量［26］。直流故障发生后,故障频域的附加网络可等效为在故障点处叠加一个电压源［27］,本文仅针对一个特定频率f的附加网络进行分析。

1.2.1 区内故障分析

以图1 中Line1 区内两极故障为例,故障附加网络如图2 所示。图中:L1和L2为线路两侧限流电抗器电抗值；Zm和Zn分别为母线到故障点的等效高频阻抗；F为故障点；Rg为过渡电阻；C1和C2为整流器端口电容；Z3和Z4分别为m和n母线所连接的另一条线路的等效高频阻抗；UF为故障点处高频电压分量；Imp和Imn分别为m侧母线流向线路的正、负极高频电流；Inp和Inn分别为n侧母线流向线路的正、负极高频电流。

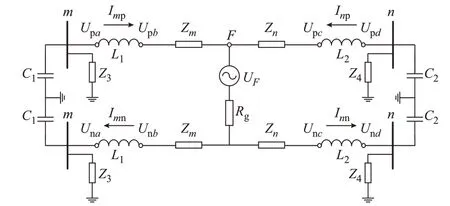
图2 区内故障时频域的附加网络Fig.2 Additional network in frequency domain during internal faults

由图2 可知,m、n背侧到接地点的等效高频阻抗ZM、ZN可由下式表示:

式中:ω为角频率。

可得,m侧和n侧正极限流电抗器左右两点对地电压分别为:

式中:Upa和Upb分别为m侧正极限流电抗器两端对地高频电压；Upc和Upd分别为n侧正极限流电抗器两端对地高频电压；下标a、b和c、d分别表示m侧和n侧限流电抗器的左、右两端。

若ZM和ZN为感性阻抗,则有

式中:|Upa|和|Upb|分别为m侧正极限流电抗器两端对地高频电压的模值；|Upc|和|Upd|分别为n侧正极限流电抗器两端对地高频电压的模值。

根据式（3）可得,系统发生区内故障时,m侧和n侧正极限流电抗器两端对地高频电压有以下关系:

同理,系统发生区内故障时,m侧和n侧负极限流电抗器两端对地高频电压Una、Unb、Unc、Und有以下关系:

式（4）和式（5）说明,发生区内故障时,线路两侧限流电抗器靠近故障点一端的对地高频电压模值大于靠近母线一端的高频电压模值。

1.2.2 区外故障分析

由图3 可知,发生反向区外故障且ZM和ZN为感性阻抗,则有

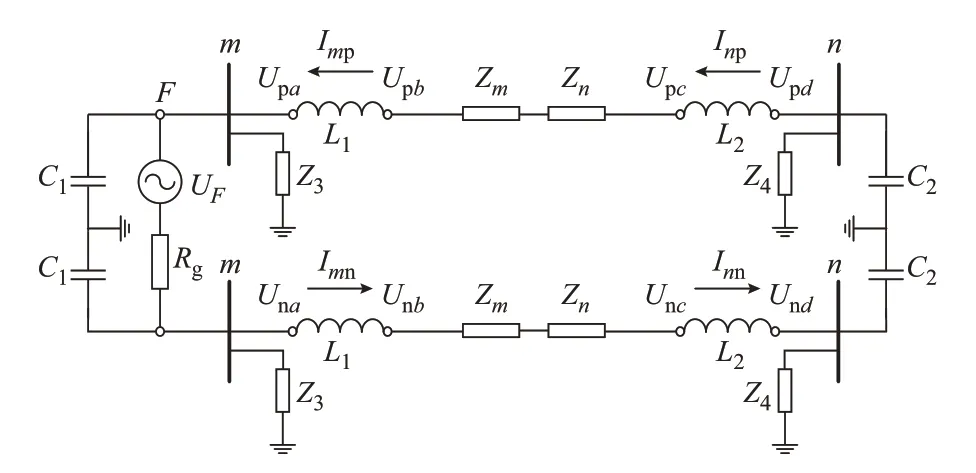
图3 反向区外两极故障时频域的等效附加网络Fig.3 Equivalent additional network in frequency domain during reverse directional external faults

根据式（6）可得,系统发生区外故障时,m侧和n侧正极限流电抗器两端对地高频电压有以下关系:

同理,系统发生区外故障时,m侧和n侧负极限流电抗器两端对地高频电压有以下关系:

式（7）和式（8）说明,发生区外故障时,限流电抗器距离故障点最近的端对地高频电压最大,并随着故障点距离增大对地高频电压减小。

1.2.3 单极故障时的非故障极线路分析

直流线路在电能的传输过程中,正负极线路存在耦合［27］,当单极故障发生时,在故障极,闭合回路中的高频电流IF1和IF2产生交变磁场Bi。如附录A图A1 所示,由于磁场作用,会在非故障极感应出高频电压Ui。图4 进一步呈现了单极故障时,非故障极的故障频域附加网络［25］。

图4 非故障极的故障频域附加网络Fig.4 Additional network in fault frequency domain of non-fault pole

由图4 可知,单极故障时非故障极的故障特征与区外故障相类似,有

式中:|Ua|和|Ub|分别为非故障极m侧正极限流电抗器两端对地高频电压的模值；|Uc|和|Ud|分别为非故障极n侧正极限流电抗器两端对地高频电压的模值。

综上,区内外故障限流电抗器两端对地高频电压模值的大小关系如表1 所示。

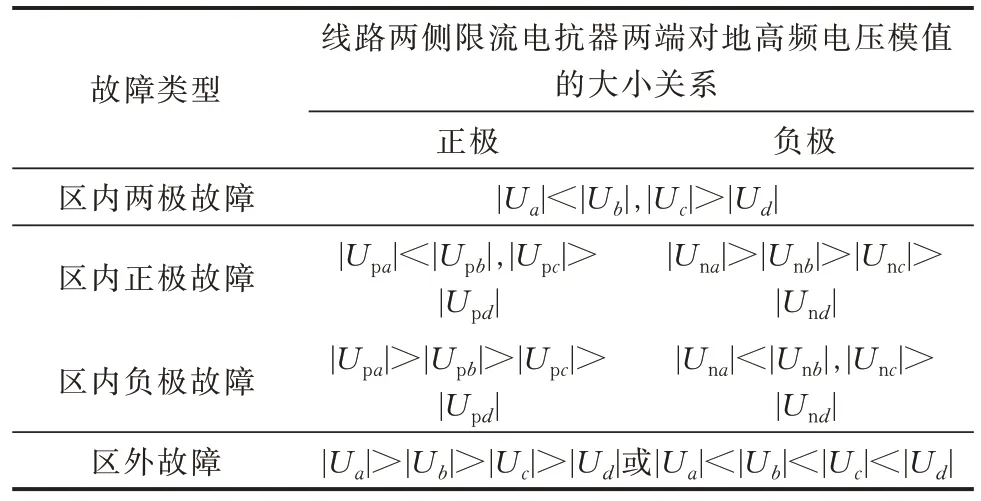
表1 区内外故障限流电抗器两端对地高频电压模值的关系Table 1 Relationship of amplitude of high-frequency voltage-to-ground between two ends of fault current limiting reactor for internal and external faults

2 容性阻抗和频率选取

2.1 容性阻抗

系统故障的暂态过程与系统的换流器有着密不可分的关系,现有工程在交流供电侧常用的换流器有模块化多电平换流器（modular multilevel converter,MMC）和两电平VSC。因其在拓扑结构上的区别,故障时的暂态电路模型也有着很大不同［6］。如图5 所示,MMC 的故障暂态电路可等效为RLC 串联电路。图中:Ls为交流系统到换流器的等效电感；La为桥臂电感；SM1 为MMC 的子模块；If为故障电流。而对于VSC、AC/DC 和DC/DC 的故障暂态电路,可等效为单个的电容电路。

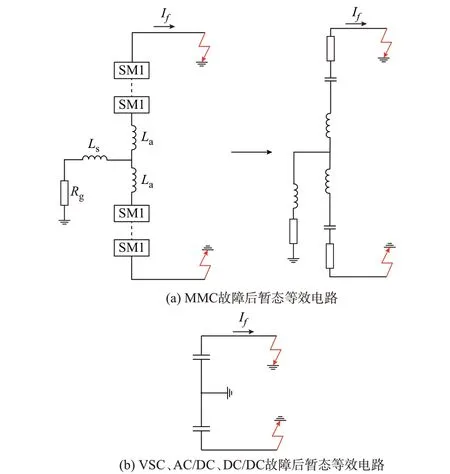
图5 故障后整流器暂态等效电路Fig.5 Transient equivalent circuit of rectifier after fault

第1 章中,判断区内外故障所用的公式是假设m、n背侧阻抗ZM和ZN为感性阻抗时成立的。因此,本文提出的保护方案能够较好地适用于两端或者多端的MMC 系统。而对于存在VSC、AC/DC 和DC/DC 的两端或者多端系统中,由于换流器端口电容的存在,会使得ZM和ZN呈容性,需要进一步考虑解决方案。下文以图2 为例,考虑到Z3为另一线路的等效阻抗且存在限流电感,故Z3在高频电路下呈感性阻抗,但因其并联电容C1的存在,则可能使得ZM呈容性,导致式（4）、式（5）不成立。

为解决m、n背侧阻抗呈容性导致无法利用式（4）、式（5）、式（8）、式（9）判断区内外故障的问题,需考虑这样一种场景:以图1 中Line1 故障为例,故障附加网络如图2 所示,C1为VSC 端口电容,C2为AC/DC 端口电容；由于直流微电网线路较短,可忽略Z3、Z4中的线路阻抗,则Z3=Z4=j2ωL（即限流电抗器的阻抗）。对于m侧（n侧可同理得到）,区内故障时有|Upa|<|Upb|,即

式中:ω1为多端系统临界角频率；L为限流电抗器电抗值；C为换流器端口电容。

考虑到存在两端系统的情况,需计算仅存在C1和C2时的角频率ω2:

由式（11）、式（12）可以看出,若L、C越小,则|Upa|<|Upb|时的临界角频率越大。一般情况下,限流电抗L取5～10 mH。这里考虑较为严重的情况,L取5 mH,计算在不同电容C下,使得|Upa|<|Upb|时的临界频率,结果如表2 所示。表中:f1为多端系统临界频率；f2为两端系统临界频率。

表2 不同电容下的临界频率Table 2 Critical frequencies with different capacitance

由表2 可知,随着电容减小,临界频率增大。但换流器上的并联电容一般不会小于0.1 mF,因此,频率取500 Hz 以上能够较好地消除m、n背侧并联电容的影响。

同样,由式（11）、式（12）可以得到,当ω2LC>2.5 时,本文保护理论成立。L取值一定时,换流器并联电容C越大,角频率取值范围越大。

2.2 频率选取

结合上述结论,在选择频率f时有以下要求:

1）消除母线m、n背侧并联电容的影响,由2.1节分析可知,选择频率f应大于500 Hz；

2）在正常运行时,要求系统产生该频率的高频分量模值较小；

3）在发生故障后,要求系统产生该频率的高频分量的模值较大,易于故障判别。

附录A 图A2 所示为利用傅里叶算法实时计算出的不同频率下,正常运行时的限流电抗器对地电压模值大小［27］。由图A2 可知,频率为500 Hz 正常运行时,限流电抗器对地电压的最大值在3 V 左右,当大于1 500 Hz 正常运行时,限流电抗器对地电压的最大值在1 V 左右。在该仿真实验场景下,正常运行时1 500～3 000 Hz 的高频对地电压模值的最大值相差不大,因此,选取1 500 Hz 频率作为保护方法所用的频率。这样,既能保证线路一侧的限流电抗器阻抗的模值远大于m、n背侧容性阻抗的模值,即满足式（4）、式（5）、式（7）—式（9）,又能保证在故障后有较高模值的高频量易于故障判别。

2.3 新能源接入电网对高频分量的影响

新能源接入电网的结构与参数变化较为频繁,会在系统中产生高频分量。

首先,需考虑关于分布式电源及负载投切问题。如图1 所示,以风机退出运行瞬间为例,相当于在保护1、保护10 的反向区外加入了一个类似阶跃的信号,会使得系统高频分量突增。由本文的保护理论分析可知,该情况为保护1、保护10 发生反向区外故障。

其次,关于系统结构变化,即系统开环、闭环瞬间。由于隔离开关位于限流电抗器靠近母线侧,在开环、闭环瞬间与分布式电源及负载投切相类似,发生反向区外故障。

最后,外界环境因素的变化（风速和光照强度的变化）及自身控制策略的影响会输出一定的高频分量。外界环境变化与投切问题和系统结构变化相类似,相当于保护的区外故障。而在换流器脉宽调制（pulse width modulation,PWM）的调制方式中,开关频率通常大于5 kHz 甚至达几十kHz［28］。本文所选取的高频频率为1.5 kHz,躲过了因外界环境因素的变化及自身控制策略影响所产生的高频谐波范围,故影响较小。

3 基于限流电抗器对地高频电压保护方案

3.1 故障启动判据

当直流线路发生短路故障时,会在系统中产生较为丰富的高频分量,可以利用这一特征构造故障启动判据,如式（13）或式（14）所示。

由式（13）、式（14）可知,电压定值根据b、c两点对地电压选取,以b点对地电压为例:

式中:Im为m侧高频电流。

由2.1 节分析可得,1-2ω2LC恒小于0,当Im、ω和L一定时,换流器并联电容C越大,|Ub|越小,电压定值取值越小。

分布式电源及负载投切和系统结构变化时,类似发生区外故障。因此,本文保护启动仅需躲过稳态正常运行时的最大值,即外界环境因素的变化及自身控制策略产生的高频分量最大值。假设系统正常运行时,b、c点对地电压的最大值为|UM|,保护启动的整定值为|Uset|=k|UM|,其中k取2～5,本文k取5。

3.2 故障识别与选极

由第2 章分析可知,在不同故障类型下,线路两侧的限流电抗器两端对地高频电压模值存在差异。以区内故障为例,可推导得到:

由式（16）可以看出,当选取的频率一定时,判据比值只与背端阻抗和限流电抗器的大小有关。

由本文2.1 节可得,当ω2LC>2.5 时,有|Upb|/|Upa|>1 且|Upc|/|Upd|>1。即本文所选1 500 Hz 频率下,定值为1 的适用系统参数范围为LC>3×10-8。而一般情况下,在1 500 Hz 以上的频率范围,恒有LC>3×10-8。

可利用该性质来构造识别区内外故障的判据W1、W2、W3、W4,如式（17）所示。

式中:n为时间窗内采样点总数。故障识别与选极判据如式（18）所示。

4 仿真实验

本文在MATLAB/Simulink 中,搭建了电压等级为±500 V 的五端环型直流微电网仿真模型,并在RT-LAB 中模拟现场运行采样误差、干扰等。采用频率为1 500 Hz 高频信号；数据采样频率为10 kHz。在t=1.5 s 时发生故障,仿真模型参数如附录A 表A1 所示。

4.1 正常运行时系统的高频分量

直流微电网中包含风机、光伏等分布式电源。在正常运行时,分布式电源由于外界环境因素的变化,其输出会产生一定的高频分量。包括:1）风速的变化导致风力发电机输出功率的变化,使其产生一定的高频分量；2）光照强度的变化同样会导致光伏发电输出功率的变化,使其产生一定的高频分量。

附录A 图A3 所示为风速、光照强度在1.5 s 同时变化时,产生的对地高频电压。其中,风速由10.5 m/s 增加到13 m/s；光照强度由1 000 W/m2增加到1 200 W/m2。由图A3 可知,正常运行时外界产生的b、c点对地高频电压的最大值|UM|=1 V,可得本文阈值|Uset|=5 V。

4.2 区内故障

直流微电网换流站中存在许多电力电子元件,需要在故障时迅速切除故障,防止较大的故障电流损坏电力电子元件。首先,对区内故障进行仿真实验。在设定的阈值下,由附录A 图A4—图A6 可以看出,发生区内单极故障和两极故障时,b、c点对地电压在故障后0.1 ms 内超过阈值,具有较好的速动性；发生200 Ω 过渡电阻故障时,保护能够正确动作,具有较好的抗过渡电阻能力。

表3所示为不同故障类型和故障电阻下的区内故障及其启动判据的动作时间。在故障电阻为100 Ω时,仍具有较好的灵敏性和速动性。对于各种情形的区内故障,各线路的故障判别结果如表4 所示。

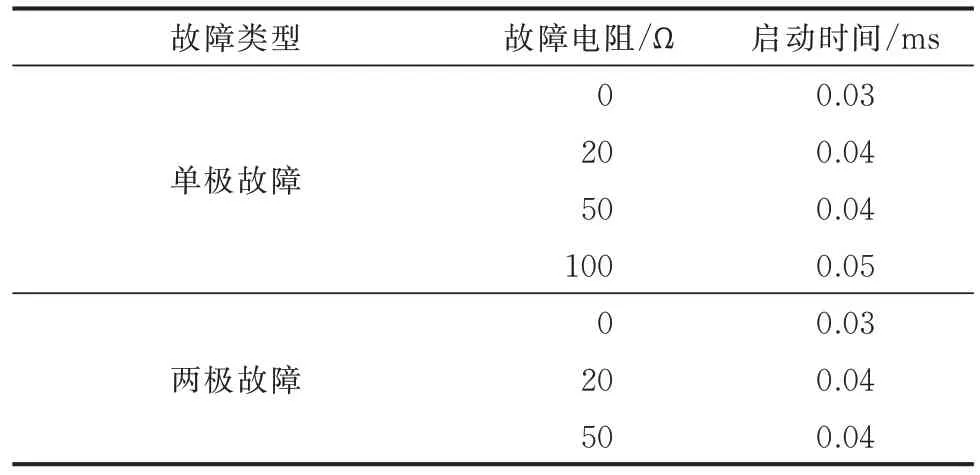
表3 不同故障类型下的保护启动判据动作时间Table 3 Operating time of protection start criterion with different fault types

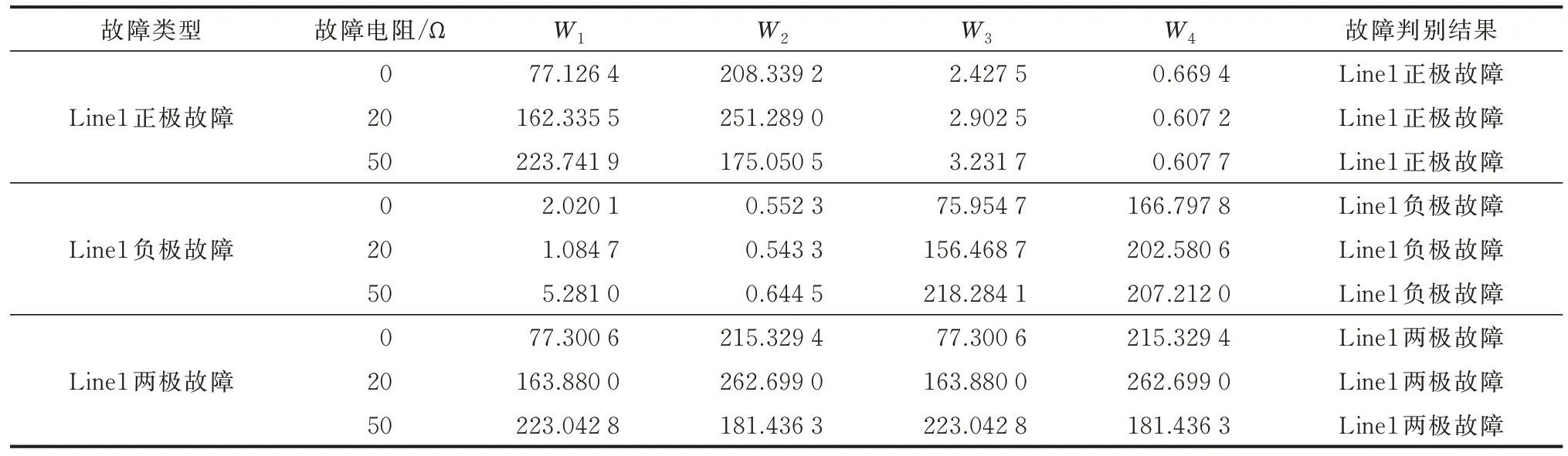
表4 区内故障判别结果Table 4 Identification results of internal faults

4.3 区外故障

以Line5 发生两极故障为例,对于Line1 而言,Line5 发生两极故障为区外故障,Line1 的正、负极线路两侧限流电抗器两端对地的高频电压模值波形如附录A 图A7 所示。由图A7 可见,即使b、c两点的对地高频电压超过设定的阈值,但因两侧限流电抗器两端的对地高频电压满足式（18）的区外故障判断逻辑,线路Line1 上的保护不动作。

对于各种情形的区外故障,故障判别结果如表5 所示。对于Line1 线路,其他线路故障都属于区外故障,会出现式（18）区外故障的判断逻辑和Line1的保护不启动的情况。因此,发生区外故障时保护不误动。

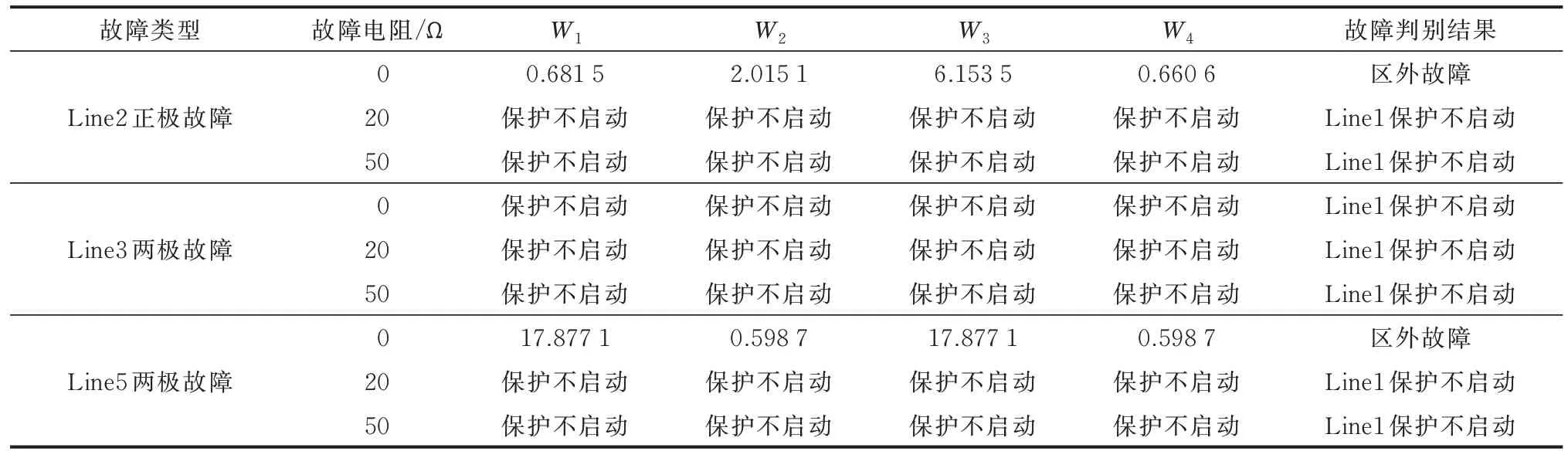
表5 区外故障判别结果Table 5 Identification results of external faults

4.4 运行模式变化对故障判断的影响

环形直流微电网有多种运行方式,其中包括开环运行和闭环运行,保护方案需要在这些运行方式下正确动作,且在切换运行方式时不误动。本节验证了不同运行方式下保护的可靠性,主要考虑以下场景:

场景1:开环运行,在Line5 退出运行时,同样在1.5 s 发生故障,验证Line1 上的保护是否正确动作。

场景2:由开环运行变为闭环运行,Line1 在1.5 s 前退出运行,系统为开环运行,在1.5 s 时刻Line1 投入运行,系统变为闭环运行,验证Line1 投入时Line1 上的保护是否误动。

场景3:由闭环运行变为合开环运行,Line5 在1.5 s 前投入运行,系统为闭环运行,在1.5 s 时刻Line5 退出运行,系统变为开环运行,验证Line1 投入时Line1 上的保护是否误动。

附录A 图A8 表明,无论是何种运行方式,该保护方案均能准确判别故障,不受系统运行方式影响。

由附录A 图A9（a）可知,由开环运行变为闭环运行时,保护1、2 测量到的b、c两点对地高频电压模值最大值在1～2 V,本文设定的阈值为5 V,因此,保护1、2 不会启动,并且如3.1 节所述,该过程类似发生区外故障,保护不会动作。由图A9（b）可知,由闭环运行变为开环运行时,如3.1 节所述,该过程类似发生区外故障,即|Ua|<|Ub|<|Uc|<|Ud|,保护不会动作。

4.5 通信延时对保护的影响

光纤中信号传输的速率约为2.04×108m/s［25］,可采用专用光纤通道进行传输,以保证信号传输的速率。由于在直流微电网中线路较短且线路两端均设置保护启动元件,两端只需传递动作逻辑信号,对数据同步无严格要求。本文所选时间窗为2 ms,由表4 可知,保护可在0.03～0.05 ms 启动,总体的线路保护方案可在2 ms 左右迅速动作,因此,在动作时间上满足保护的要求。

4.6 数据窗的选取及影响

数据窗长度的选择会直接影响到保护的性能。若数据窗选择过短,则高频分量计算时用到的基频频率范围有限；若数据窗选择太长,则对保护速动性有影响。因此,本文折中选择了2 ms 作为本文保护所用数据窗。

傅里叶算法中,令基频频率为500 Hz,则基频周期为2 ms,谐波次数取为3,可得本文用到的1 500 Hz 高频分量。算法数据窗需根据基频周期选取,同样设为2 ms。若数据窗选取小于2 ms,则数据窗为1 ms 时,可选择的最小基频频率为1 000 Hz,可用频率范围减小,且无法获取本文所选频率。若数据窗选取大于2 ms,以正极故障为例得到区内故障4 ms 后的限流电抗器对地高频电压波形如附录A 图A4（a）所示。由仿真波形可得,故障后的2 ms内,故障线路的限流电抗器b、c点对地高频电压在一定范围内振荡,始终大于a、d点对地高频电压；故障后的2 ms,故障线路的限流电抗器b、c点对地高频电压开始衰减到与a、d点对地高频电压相近,根据式（18）判据可准确判断故障,但为了满足保护的速动性要求,满足本文故障识别条件的可用时间窗长取2 ms 较为合适。

4.7 与现有边界保护方案对比

文献［29］利用线路两端高频功率幅值作为启动判据,根据两端高频功率差异判别区内外故障。附录A 图A10 给出了发生金属性故障、过渡电阻为20 Ω、系统由开环变为闭环时两端高频功率幅值的波形。由图A10（a）、（b）可知,高频功率受过渡电阻影响极大,仅当过渡电阻为20 Ω 时保护就可能拒动；由图A10（c）可知,系统由开环变为闭环时,会产生较大的高频功率幅值,可能会使得保护误动作。

文献［18］利用两侧限流电抗器电压进行故障检测,当限流电抗器电压大于阈值时保护动作。附录A 图A11 给出了过渡电阻为150 Ω 且正向区外故障时,系统由开环变为闭环时的限流电抗器电压波形。由图A11（a）、（b）可知,随着过渡电阻增大,若要判别高阻故障,需将阈值设小,而当该故障发生在正向区外或反向区外出口处故障时,若上、下级保护因某些原因拒动,则本线路保护可能会因为电压达到保护阈值而误动。由图A11（c）可知,系统由开环变为闭环时,会在限流电抗器两端产生大电压,可能会使得保护误动作。

由附录A 表A2 可知,本文利用限流电抗器对地高频电压的保护方法,在不同故障场景和运行方式下均能可靠进行故障识别和故障选极,且具有较强的抗过渡电阻能力。