基于改进多分类器的用户电表采集数据修复方法

唐冬来，李 玉，何 为，刘友波，欧 渊，吴 磊

（1.四川中电启明星信息技术有限公司,四川省成都市 610074；2.国网四川省电力公司,四川省成都市 610041；3.四川大学电气工程学院,四川省成都市 610065）

0 引言

用户电表是指安装在用电客户进户线处的电能计量装置,用于计量用电客户的电能消耗情况,具有地理位置分布广泛、类型众多、数量庞大等特点［1-2］。在推动“双碳”战略和建设新型电力系统的背景下,用户电表作为电网末端监测的重要设备,是推动“电力减碳”和新型电力系统建设的关键环节之一［3-4］。为保障电网末端家庭智慧用能、分布式能源服务、电动汽车与电网互动（vehicle to grid,V2G）等新型电力系统新兴业务的开展,须通过新一代智能电表的采集数据指导配电台区“源网荷储”协同控制［5-6］。新一代智能电表以每天96 个时段频次采集用户的电气数据,采集频次高、数据传输信道压力大。在数据采集过程中,受电表故障、信道噪声等因素影响,用户电表采集数据存在大量缺失、错误等异常情况,电表全量数据的采集成功率为96.5%,电表远程付费控制单次成功率为96.2%［7-9］,供电公司的用电信息采集系统须多次下发付费控制指令方能执行成功,进而影响配电台区“源网荷储”控制的准确性。

用户电表采集异常数据处理的方法分为删除法与填补法两类。其中,删除法将用户电表采集异常值的周期数据项删除,以满足计算条件。但该方法会造成真实数据丢失,导致计算结果偏差更大［10-11］。填补法采用近似值来填补用户电表的异常值,分为插值法和机器学习法。插值法利用均值、分位数、中值等进行插补,具有逻辑简单、计算速度快的特点,但该方法将异常值视为线性变化值,未考虑用户电表采集数据时序中蕴含的变化规律,异常值修复误差大［12-15］。机器学习法考虑了用户电表采集数据时序变化规律,采用贝叶斯网络、K近邻、长短期记忆（long short-term memory,LSTM）网络等模型进行训练,提高了异常值的修复精度［16-18］。但上述方法将用户电表数据作为一个整体进行修复,未考虑不同异常类型用户电表采集数据的差异,数据修复准确性不高。

多分类器是一种组合式的模型训练方法。该方法将用户电表采集异常数据集训练成不同的子集,每个子集的训练程度均有差别。然后,采用子集修复不同时段的用户电表采集异常数据,进而形成更准确的用户电表采集异常数据修复结果［19］。多分类器在电力系统的故障预警、负荷预测等方面得到了应用,表明多分类器能够较好地学习用户电表真实数据特征［20］。但采用多分类器进行用户电表数据修复训练时,难以找到用户电表真实时序数据来训练模型。

本文在多分类器的基础上,采用变分自编码器（variational autoencoder,VAE）［21］设计了一种用户电表采集数据修复方法。首先,该方法将用户电表采集数据中的完整区块作为训练子集,将其缩减后作为子分类器,在此基础上建立分类器集合,并对用户电表采集异常数据进行分类。然后,通过VAE 构建模型训练子集,从而在用户电表采集异常数据中学习数据的真实变化规律。最后,对用户电表采集异常数据进行修复,形成用户电表采集数据修复集合。所提方法在无监督环境下训练与修复,可提高用户电表采集数据修复的准确率。

1 用户电表采集数据修复流程

基于多分类器的用户电表采集数据修复方法流程图如图1 所示。

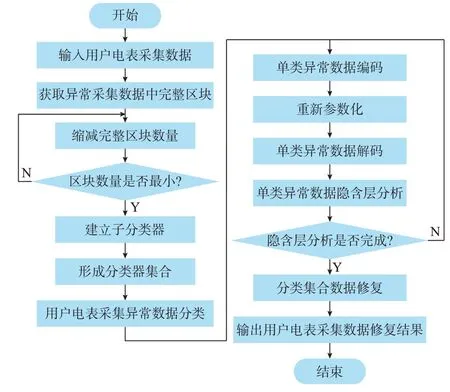
图1 用户电表采集数据修复流程图Fig.1 Flow chart of restoration of collection data from user electricity meters

1）用户电表采集异常数据分类

首先,在包含异常值的用户电表采集数据中获取不含异常数值的数据段,将其作为完整数据区块,以及分类训练的备选子集。然后,缩减用户电表采集数据完整区块的数量,直至有效完整区块数量最小,以降低模型训练时间,提高模型运行性能。在此基础上,针对每个有效的完整区块分别建立不同的子分类器。最后,在计及子分类器权重的情况下形成分类器集合,并以此对用户电表采集异常数据进行分类。

2）用户电表采集异常数据修复

首先,对单类用户电表采集异常数据进行编码,通过输入的用户电表采集数据得到标准差和均值。然后,对单类用户电表采集异常数据重新进行参数化,通过用户电表采集数据的标准差和均值生成用户电表采集数据中的蕴含变量。在此基础上,进行单类异常数据解码和隐含层信息分析,直至所有分类完成隐含层信息分析。最后,通过分类集合对用户电表异常数据进行重构与修复,并输出修复结果。

2 用户电表采集异常数据分类

2.1 获取完整数据区块

在用户电表采集数据的过程中,受电表故障、高速电力线载波（high-speed power line carrier,HPLC）信道噪声等因素影响,造成采集异常数据的缺失、错误等［22］。若采用含异常样本的数据集训练分类模型,将导致异常数据分类性能大幅下降,对用户电表采集数据异常值的修复也不准确。因此,须采用正确的数据训练模型。

数据区块是指具有典型特征的数据区域。完整数据区块是指不含异常数值的数据区域,异常区块是指含异常数值的数据区域。本文按每天96 个时段频次采集电表数据。因此,本文完整数据区块的提取方法是将一个时间段内不含异常数值的数据作为一个完整数据区块进行提取,并以此进行模型分类训练。

用户电表采集数据异常特征分为缺失部分和异常部分。其中,缺失部分为用户电表空值数据,通过空值进行检测识别,缺失的用户电表数据异常特征属于异常样本属性集。异常数据为用户电表非空值数据,包括超过电表量测范围、台区总表与户表之和的差异超过量测阈值、三相电表总量与分量之间的差异超过量测阈值3 类,通过比较总表与户表量测数据差异阈值和量测范围进行识别,异常的用户电表数据特征不完全属于异常样本属性集。用户电表采集数据异常特征ck可表示为:

式中:di为含异常样本数据集中的第i个样本值；Ea为用户电表采集异常样本属性集；dil为用户电表采集第i个样本值的第l个异常特征值；dnull为用户电表采集数据的缺失值；“∧”表示交运算。

含异常样本的用户电表采集数据集中,每个采集样本都有异常样本属性,即每个电表异常采集曲线的数据中有不同的缺失数据点或异常数据点。若多个电表的缺失数据点或异常数据点时间相同,则构成一类异常区块,并按同一个属性子集处理。

异常区块可以视为含异常样本数据集Dall在异常样本属性子集Eb的投影,属于异常样本属性子集Eb的 第i个 样 本 值 用di［Eb］表 示,异 常 区 块Qa可 表示为:

因此,在每个用户电表采集异常区块Qa中,均包含异常数据。

用户电表采集数据第i个完整数据区块数据Qci可表示为:

式中:Dalli为含第i个异常样本的数据集；Qai为含第i个异常样本的异常区块。

2.2 缩减完整数据区块数量

通过式（3）获得的用户电表采集数据完整区块数量庞大,且多个完整区块间存在部分特征重叠,若将全部完整区块用于模型训练,将导致模型性能降低。因此,本文在全部完整区块中筛选出可以代表完整区块的典型区块,以缩减用于模型训练的完整区块数量。

缩减用户电表完整数据区块的规则为:将用户电表完整数据区块时段内的电量、电压、电流、有功功率、功率因数的每天96 个时段曲线进行比较,若短时段完整数据区块曲线与长时段曲线的一部分相似,则缩减短时段完整数据区块,从而降低完整区块数量,直至所有完整数据区块时段曲线相似度不重叠,即为最小完整数据区块数量。曲线相似度分析采用欧氏距离量度,限于篇幅,本文不再赘述。

贪心算法（greedy algorithm,GA）是一种集合覆盖算法,该方法在每一步执行过程中均求解当前局部最优状态并不断迭代,直至整体逼近最优求解。但GA 在搜索过程中若找不出满足条件的特征属性,则陷入局部收敛［23-24］。因此,本文将GA 改进为双向搜索,在传统开始点向结果点正向搜索的基础上,增加了从结果点到开始点的逆向搜索。若正向搜索和逆向搜索重叠,则完成全局逼近最优求解。

在改进GA 缩减完整区块的方法中,当输入候选完整区块Qcd不为空值时,随机构造一个包含参数集λ的完整区块Qe,并进行迭代缩减。在迭代缩减环节中,GA 集合Qci包含未被覆盖的元素集合,该元素集合中拥有的特征为Ga；通过GA 对Qci正向搜索以缩减完整区块得到Qg；通过GA 对Qci反向搜索以缩减完整区块得到Qh；正、反方向搜索均向同一方向逼近,直至Qg与Qh重叠,则完成用户电表采集数据全局逼近最优求解。

2.3 异常数据分类

以每个用户电表采集数据完整区块训练子分类器,子分类器中可充分学习到该完整区块的特征信息。因不同用户电表采集数据特征对最终分类结果的影响不同,针对每个子分类器设置不同的权重。在此基础上建立分类器集合,并对用户电表采集数据进行异常数据分类。

随机森林（random forest,RF）是一种分类器,该分类器从原始数据中提取多个训练样本,并对每个样本建立决策树进行单独训练,构建不同的训练样本集,从而扩大决策树与各子样本训练集之间的差异。然后,采用决策投票的方式组合多个决策树,从而得到样本的分类结果［25］。RF 可以处理含大量数据的用户电表采集完整区块数据,具有算法运行速度快、分类结果准确率高的特点。因此,采用RF 建立子分类器和分类器集合。

在用户电表采集数据子分类器训练中,采用信息熵衡量子分类器的重要程度,熵值越小,则子分类器的不确定性越小,即重要性越高；反之,熵值越大,则重要性越小。计算子分类器的信息熵值El如下:

式中:na为子分类器的个数；oj为子分类器j所占的信息量。

然后,计算子分类器的权重wl如下:

式中:Elj为子分类器j的信息熵值。

在用户电表采集数据子分类器训练完成后,得到nb个子分类器,并形成分类器集合,通过多数投票决策的方式得到用户电表采集数据分类器集合的最终分类结果。RF 最终的分类决策输出结果Rout可表示为:

式中:A(rj)为子分类器j决策树输出数据；rj为j决策树输出数据；wlj为不同子分类器权重。

最后,采用RF 最终的分类决策结果对输入的用户电表采集异常数据进行分类。

3 用户电表采集异常数据修复

VAE 是一种深度隐含空间的生成模型。VAE包含编码器、重新参数化和解码器3 个部分,可挖掘输入数据的规律与隐含信息,实现缺失数据的推理重构,具有强大的缺失数据修复能力［26-27］。在VAE的结构中,编码器用于对输入样本数据的方差和均值进行计算与推理；重新参数化用于计算输入样本数据方差和均值的专属正态分布特征；解码器对重新参数化的特征进行解码,重构生成数据。VAE 异常数据修复框架如图2 所示。图中:m为用户电表采集异常分类数量；zm为输入VAE 的原始数据分类样本；fm为VAE 重新参数化的采样变量；zam为VAE输出的生成修复样本数据。

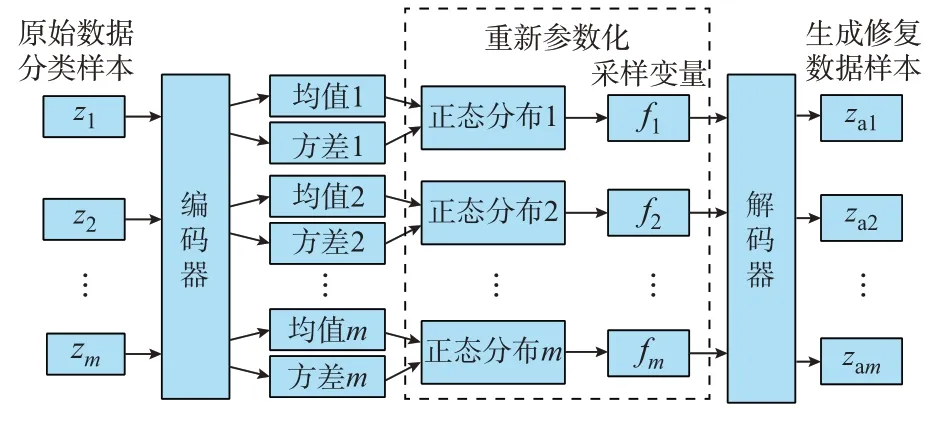
图2 VAE 异常数据修复框架Fig.2 Framework of VAE abnormal data restoration

VAE 中,编码器用于计算用户电表采集异常原始子分类样本的方差和均值；重新参数化用于在用户电表采集异常数据子分类的专属正态分布中进行采样变量获得推理特征Cm；解码器则对推理特征进行解码,得出不同分类的用户电表采集异常数据类型的隐含变量Sm:

式中:δm为分类m的用户电表采集异常数据方差；hm为分类m的用户电表采集异常数据均值。

通过解码器得到各子分类用户电表采集异常数据的隐含变量后,考虑各子分类隐含变量之间的关系,对所有子分类集合进行整体解耦,从而避免单个子隐含类解耦存在的关联分析不足的问题。

在分类集合解耦过程中,各子分类的隐含变量相互独立,其并发似然概率为各子分类概率的积。因此,各子分类的改变不会影响其他子分类,即不同用户电表采集异常数据子分类VAE 训练程度不同,从而满足各子分类用户电表采集异常数据特征。然后,采用分类集合进行整体解耦并生成修复数据样本。分类集合整体解耦的目标函数Bout可表示为:

式中:nh为VAE 中子分类的数量；ng为VAE 每次训练的子分类数量；vm为子分类m的修复数据边界值；ψ为超参数；um为子分类m的最小正态分布。

VAE 训练的目标为重新参数化中的用户电表采集数据正态分布值与正态分布的相对熵散度最小。VAE 解码器输出的用户电表采集修复数据与编码器输入的用户电表采集数据相似。VAE 损失函数lall可表示为:

式中:lstudy为学习损失,即确保VAE 重新参数化中学习的正态分布、正态分布的相对熵散度与真实值相似；lrebuild为重建损失,即确保VAE 解码器输出与编码器输入的用户电表采集数据相似。

式中:nd为VAE 中学习的用户电表采集异常数据分类数量。

式中:no为VAE 中重建的用户电表采集异常数据分类数量。

4 算例分析

采用中国西部某城市小区的用户电表真实采集数据验证本文所提方法。用户电表异常数据的真实值无法获取,故采用完整的用户电表采集数据来构建缺失数据集,并将修复后的用户电表采集数据与真实数据进行比较,以验证所提方法的有效性。考虑城市小区总表和用户电表线损校验规则等情况,本文方法训练和数据修复时均采用城市小区电表的所有数据。训练样本选择的用户电表数量为该配电台区下276 个单相用户电表2022 年全年的数据。采集频次为每天96 个时段,采集和修复的数据类型为电压、电流、有功功率、无功功率、功率因数、电量。所用的276 个用户电表数据自身带有一定缺陷,经人工依据行业标准校核后,将该数据假定为真实数据。

本文仿真方法的硬件平台采用Intel Core i7 8700 中央处理器,处理器频率为3.2 GHz,内存为16 GB；软件平台操作系统为Windows 10,算法采用Python 实现。在训练过程中,编码器层数设置为1,节点大小设置为3 000,训练次数设置为400 和800,激活函数选择Sigmoid,初始学习率设置为0.000 2,批 大 小 为64,并 与LSTM 网 络［28］、生 成 对 抗 网 络（generative adversarial network,GAN）［29］等 主 流 用户电表数据修复方法进行对比。

4.1 模型训练分析

4.1.1 缩减完整区块训练分析

在GA 训练过程中,采用精准率和召回率来衡量GA 完整区块缩减精度。其中,精准率又称查准率,是指在预测缩减完整区块的数量中,正确缩减完整区块所占的比例,其值越大,说明完整区块缩减越准确；召回率又称查全率,是指预测正确缩减的完整区块占总正确缩减完整区块的比例。采用GA 双向搜索法与集合覆盖法［30］比较精准率和召回率。集合覆盖方法在缩减数据集领域广泛应用,通用性强。因此,采用该方法与GA 双向搜索法进行比较。GA 缩减完整区块训练如附录A 图A1 所示。

由附录A 图A1 可见,在精准率方面,高精准率是缩减完整区块的基础,在GA 训练过程中,双向搜索法与集合覆盖法的精准率均维持在较高的水平。随着训练次数的增加,双向搜索法的精准率在60 次训练附近时收敛为98.6%,集合覆盖法的精准率在80 次训练附近时收敛为91.4%。在召回率方面,随着训练次数的增加,缩减完整区块的问题不断得到解决,召回率不断提升,双向搜索法的召回率在140 次训练附近时收敛为98.5%,集合覆盖法的召回率在180 次训练附近时收敛为91.5%。由此可见,在缩减完整区块中,GA 双向搜索法优于集合覆盖法。

4.1.2 异常数据分类训练分析

采用RF 进行异常数据分类训练中,训练次数和RF 分类的正确率有不同程度的影响,训练次数少于异常数据分类类别时,RF 的分类误差较大；训练次数过多时,将消耗大量的训练空间和时间资源。朴素贝叶斯分类（native Bayesian classification,NBC）算法［31］结构稳定,损失误差小,行业通用性强。因此,选择NBC 算法与RF 进行异常数据分类训练比较,异常数据分类训练分析如附录A 图A2所示。由附录A 图A2 可见,随着训练次数的增加,异常数据分类损失率不断下降,RF 异常数据分类训练次数在240 次左右时收敛在0.5%处；NBC 异常数据分类训练次数在300 次时收敛在0.7%处。由此可见,RF 较NBC 算法在更少的训练次数下取得了更少的损失误差。

4.1.3 异常数据修复训练分析

在异常数据修复训练中,损失函数包括学习损失和重建损失,训练次数对异常数据修复的影响程度不同。当模型训练次数较少时,VAE 未充分学习,不能获得最优求解；训练次数过多时,会造成VAE 过拟合。采用LSTM 网络和GAN 与VAE 进行异常数据修复训练比较,如图3 所示。

图3 异常数据修复训练分析Fig.3 Analysis of abnormal data restoration training

由图3 可见,VAE 总损失由VAE 学习损失和VAE 重建损失构成。随着训练次数的增加,VAE学习损失和VAE 重建损失不断下降,在训练次数为110 次附近时分别收敛在0.11%和0.09%处；VAE总损失在训练次数为110 附近时收敛在0.2%处；GAN 损失在训练次数为150 次附近时收敛在0.4%处；LSTM 网络损失在训练次数为180 次附近时收敛在0.5% 处。由此可见,VAE 较LSTM 网络、GAN 在更少的训练次数下取得了更少的损失误差。

4.2 异常数据修复评价分析

均方根误差（root mean squared error,RMSE）是一种衡量异常数据修复效果的指标,为修复数据值与真实值偏差的平方与观测次数比值的平方根［32］。RMSE 可减少误差互相抵消的问题,更加准确地反映用户电表采集异常数据修复误差的绝对值。 平均绝对百分比误差（mean absolute percentage error,MAPE）是用户采集异常数据修复误差百分比绝对值的平均值,用于衡量用户采集异常数据修复性能［33］。

异常数据分为缺失数据和错误数据,为了简化计算,在模拟异常数据时将用户电表采集缺失数据分为完全随机缺失（missing completely at random,MCAR）、随机缺失（missing at random,MAR）和非随机缺失（missing not at random,MNAR）3 类。其中,MCAR 中缺失数据不依赖任何变量；MAR 中缺失数据依赖其他完整变量；MNAR 中缺失数据依赖不完整的变量。将错误数据模拟为超出用户电表计量量程外的数据。

4.2.1 异常数据分类准确率分析

异常数据分类准确率是评估改进分类器异常分类是否准确的核心指标,为简化计算,将模拟的用户电表异常数据分为MCAR、MAR、MNAR、错误数据4 类,采用多分类器模型对异常数据进行分类,其异常数据分类与模拟数据类型一致,则异常数据分类准确。多分类器模型分类准确的数据与模拟数据总数的比值即为异常数据分类准确率。

在单个用户电表采集的一年245 280 条电压、电流、有功功率、无功功率、功率因数、电量数据中,每类数据各模拟1 000 条MCAR、MAR、MNAR、错误 数 据。其 中,1 月1 日 至2 月19 日、3 月1 日 至4 月19 日、5 月1 日 至6 月19 日、7 月1 日 至8 月19 日 的4 个50 天时间段内,每天分别模拟MCAR、MAR、MNAR、错误数据各20 条,模拟的数据点为时段13—20（03:15—05:00）、时 段77—88（19:15—22:00）。分别采用GA 与RF 组合的多分类器与NBC 比较用户电表采集异常数据分类准确率,如附录A 表A1 所 示。

由附录A 表A1 可见,因错误数据为超出用户电表计量范围外的数据,容易辨识,所以GA 与RF组合的多分类器与NBC 的错误数据分类一致。在MCAR、MAR、MNAR 数据中,GA 与RF 组合的多分类器利用完整区块进行训练,训练效果好于使用缺失数据训练的NBC。GA 与RF 组合的多分类器整体异常数据分类准确率为99.6%,高于NBC 方法,因此,其多分类器缺失数据分类更准确。

4.2.2 异常数据修复误差分析

1）不同类型异常数据修复分析

在真实的用户电表数据采集中,异常数据包括采集缺失数据和采集错误数据两类。假设用户电表采集成功率为96.5%,则异常数据包括采集3.5%的缺失数据和采集错误数据,若无采集错误数据,则异常数据等同于采集缺失数据。但受采集和信道噪声影响,用户电表采集数据中存在采集错误数据,因此,参照文献［34］中的最大采集错误数据率17.17%,则异常数据率为20.67%。若配电台区存在用户设备产生干扰高频电磁波的情况,则用户电表采集异常数据率高达50%［35］。因此,为验证在极端情况下用户电表异常数据修复效果,将异常数据率设定为50%。本文用户电表修复的数据包括电压、电流、有功功率、无功功率、功率因数、电量,各类数据的修复方法一致。

本文异常数据修复误差分析中,选择100 个用户电表4 天的数据,每天包含96 个时段的电压、电流、有功功率、无功功率、功率因数、电量数据。按异常率50%来模拟数据,其中,第1、3、4 天分别模拟MCAR、MNAR 和 错 误 数 据 各4 组:第1 组 为 时 段5—8（01:15—02:00）；第2 组 为 时 段13—20（03:15—05:00）；第3 组为时段29—44（07:15—11:00）；第4 组为时段57—76（14:15—19:00）。第2 天模拟MAR 数据6 组,每隔4 h 连续缺失8 个时段数据；并采用多分类器、LSTM 网络、GAN 分别进行异常数据修复,50%异常数据修复平均误差率如表1 所示。表1 可见,多分类器方法适用于用户电表的电压、电流、有功功率、无功功率、功率因数、电量数据,且在异常数据率为50%时,MAPE 为2.65%,低于LSTM 网络和GAN 方法。

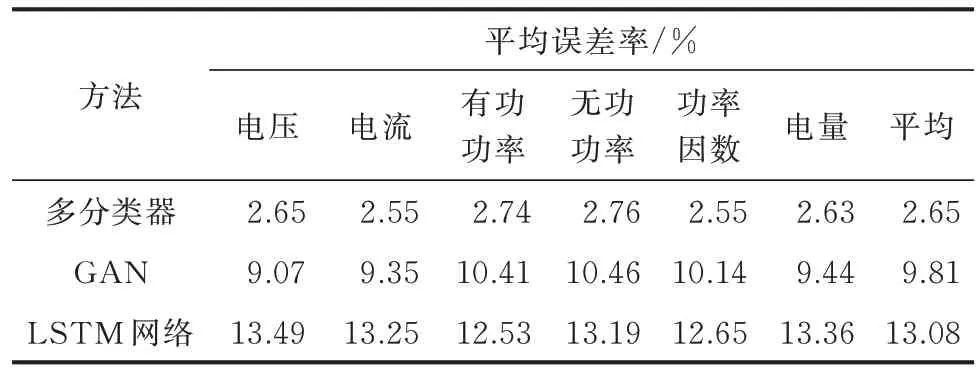
表1 50%异常数据修复平均误差率Table 1 Average error rate for 50% abnormal data restoration

2）不同异常原因数据修复分析

用户电表数据异常原因主要包括时钟超差、器件损坏等引起的电表故障和HPLC 信道噪声。不同原因造成的数据异常特征存在差异,且不同用户类型的电表采集数据也存在差异。因此,本文根据已知不同用户类型的电表故障、HPLC 信道噪声数据特征来模拟异常数据,以检验所提方法的修复效果。

本文以电表故障和HPLC 信道噪声引起的错误数据为例,进行不同异常原因数据修复分析说明。选择该城市小区内居民家庭用户、商业用户电表各10 个20 天（每天96 个时段）的电压、电流、有功功率、无功功率、功率因数、电量数据。按异常率50%来模拟数据,前10 天模拟电表故障数据,后10 天模拟HPLC 信道噪声数据,每天的异常数据分 为4 组:第1 组 为 时 段5—8（01:15—02:00）；第2 组 为 时 段13—20（03:15—05:00）；第3 组 为时段29—44（07:15—11:00）；第4 组为时段57—76（14:15—19:00）。采用多分类器、LSTM 网络、GAN 分别进行异常数据修复,不同异常原因数据修复分析如表2 所示。

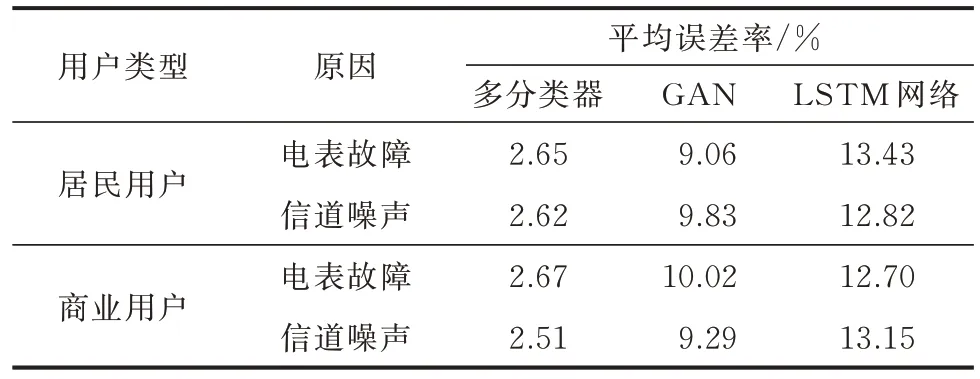
表2 不同异常原因数据修复分析Table 2 Data restoration analysis of different abnormal causes

由表2 可见,采用多分类器方法,在电表故障异常数据为50%的情况下,居民用户电表的MAPE 为2.65%,商业用户电表的MAPE 为2.67%；在信道噪声异常数据为50% 的情况下,居民用户电表的MAPE 为2.62%、商业用户电表的MAPE 为2.51%。该方法的数据均优于GAN 和LSTM 方法,且在处理信道噪声数据修复时的MAPE 小于电表故障数据。

3）异常数据修复结果分析

限于篇幅,本文以用户电表有功功率曲线修复为例,进行异常数据修复说明。选择一个用户电表4 天（每天96 个时段）的有功功率数据,根据表1 的数据模拟规则,按天依次模拟50% 的MCAR、MAR、MNAR 缺失和错误数据,并采用多分类器、LSTM 网络、GAN 分别进行异常数据修复,异常数据修复曲线如图4 所示。

由图4 可见,在50%的用户电表采集数据异常率下,LSTM 修复方法误差较大,尤其在该用户的早、晚用电高峰期修复数据功率曲线偏差大。相较之下,GAN 修复方法采用了判别网络进行生成数据修复,修复后功率曲线偏差较小。而多分类器方法按不同的用户功率数据分类进行训练并进行功率曲线修复。因此,本文所提多分类器方法修复的功率曲线偏差最小。

4）不同异常率下的修复误差分析

在不同异常率的情况下,用户电表采集数据修复方法的RMSE 和MAPE 均不同。配电台区内用户设备产生高频电磁波的强度与用户电表采集异常数据率相关。而异常数据率过大时,会造成VAE 编码器推理得到方差和均值误差超过上限,导致VAE解码器生成的数据MAPE 过大,数据无法使用。用户电表在高频电磁波干扰的极端条件下,异常数据率高达50%。为验证在极端情况下用户电表异常数据修复效果,将用户电表采集异常数据率设定为10%～70%,并分别采用多分类器、LSTM 网络、GAN 进行数据修复,其修复RMSE 和MAPE 分别如表3、表4 所示。

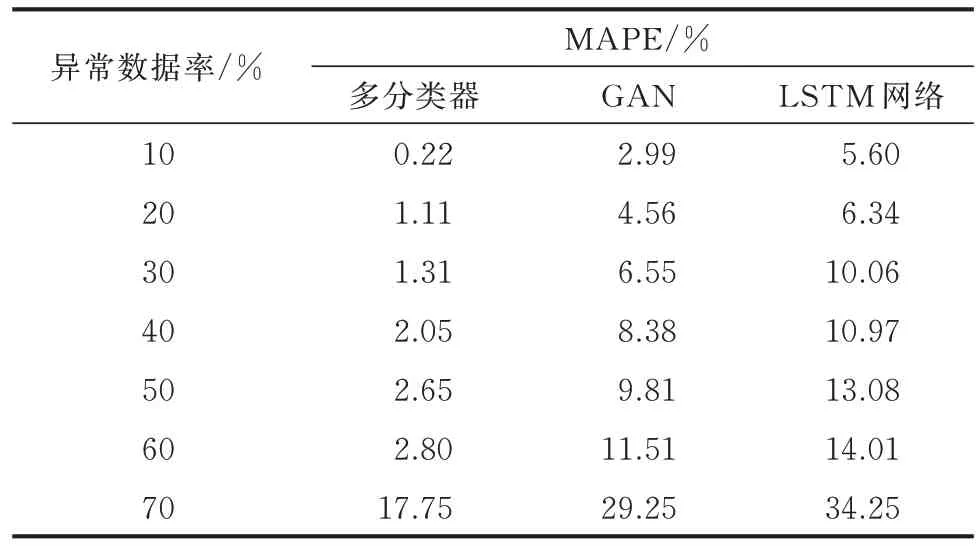
表4 异常数据修复的MAPETable 4 MAPE of abnormal data restoration

用户电表数据包含多种异常数据类型,而每种异常数据均具有不同的典型特征。所提方法在训练过程中,模型通过历史数据充分学习到每类异常数据的特征,并根据不同的用户电表异常数据类型选用与之对应的VAE 推理重构数据。随着异常数据率的增加,编码器推理得到方差和均值误差不断增大,而解码器生成的误差也越大,即可信度越小。图4 中,异常数据时间段越长,VAE 修复数据误差越大。由表3、表4 可见,在异常数据率为10%的情况下,多分类器异常数据MAPE 为0.22%,较GAN、LSTM 网络方法分别减少2.77%、5.38%。在实际工程应用中,用户电表异常数据率通常在30%以内,而在高频电磁波干扰的极端条件下,异常数据率高达50%。在考虑异常数据率裕度的情况下,将异常数据率上限设置为60%。在此条件下,异常数据分类依赖历史数据训练得出,VAE 推理得到方差和均值误差增大,造成了解码器生成的误差已接近工程应用上限,所提方法异常数据的MAPE 为2.8%,较GAN、LSTM 网络方法分别减少了8.71%、11.21%。电表数据MAPE 为3.5%时,仍可进行远程付费控制、线损分析等工作。由此可见,在异常数据率为60%时,本文方法MAPE 为2.8%,仍满足工程应用要求,且修复精度较GAN 和LSTM 高。而在异常数据率为70%时,所提方法的VAE 推理得到的方差和均值误差已超过上限,其解码器生成的MAPE 为17.75%,已不能满足工程应用要求。

5 结语

针对当前用户电表采集数据修复方法中存在的时序变化规律挖掘不足、异常值修复误差大的问题,提出了一种基于改进多分类器的用户电表采集数据修复方法。该方法对多分类器结构进行了改进,将用户电表采集数据中的完整区块用于训练模型,以减少异常数据分类和修复误差；通过VAE 学习每类异常数据的变化规律,并采用分类集合方式生成修复数据。算例以某小区用户电表进行仿真,所提方法异常数据修复质量与RF 和VAE 训练程度相关,其训练程度越高,则所提算法异常数据修复误差率越小。算例结果表明,在不同异常数据率下,该方法较LSTM 网络、GAN 具有更好的异常数据修复效果。

在用户电表异常数据率越限时,所提方法数据修复误差较大。后续研究重点为优化VAE 结构,从而降低所提方法在用户电表异常数据率越限时的修复误差。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。