多孔对电磁波CT剖面拼接的影响因素及拼接方法

江振寅，姜 杰，郑 军，田必林

（1.中国煤炭地质总局湖北煤炭地质局，湖北 武汉 430070；2.湖北煤炭地质物探测量队，湖北 武汉 430200）

1 引言

井间电磁波CT成像是高效探测地下介质电磁特性的地球物理方法［1］，其主要原理就是利用一定频率的电磁波分别在两个钻孔发射和接收，根据不同位置接收到场强的大小，对两孔之间电磁波吸收系数进行处理来确定地下不同介质分布，以此来精确地界定地下目标体的属性［2］。井间电磁波CT法以其抗干扰能力强，不受地形限制等优势［3］，在工程、煤炭、油气和金属矿产等资源勘探开发领域以及水文工程方面都得到了广泛的应用，并取得了较好的效果［4］。

通过收集的资料来看，近年来井间电磁波CT研究工作多集中于单对孔反演理论研究，在实际工程勘察工作中，常常需要在同一个工作区完成几对钻孔乃至几十对钻孔的电磁波CT成像测量，对岩溶、破碎、构造等地质结构进行勘查，目前最常用的做法就是对每一个孔对的剖面进行单独成像单独解释［5］。但单孔对成像往往不能满足综合解释的需要，有时需要将相邻的孔对相互连接成为一个完整剖面，而在连接孔处的成像结果却常常不吻合，相邻孔对之间的背景值差异过大，无法连接，以至于连接剖面的成像结果遭到质疑［5］。针对这类问题，相关资料显示，2010年雷旭友［6］提出多源多孔对电磁波CT联合反演成像的方法，将采集的原始数据进行简单的组合，对因迭代次数、随机误差等方面因素所引起的相邻孔对成像结果不吻合现象具有较好的消除作用，反演的成果可在数值上综合反映地下地质体共同的特性，对研究地质体延伸、横向变化具有实用价值，但该方法最后并未得到推广应用。

本文从单孔对入手，从反演方法和初始场强E0两个方面对可能导致相邻钻孔拼接不吻合的因素进行分析，探索寻求实现多孔对电磁波CT剖面拼接的方法，并结合工程勘察中既有数据，分析拼接效果，为今后多孔对电磁波CT成果解释和判断提供参考。

2 电磁波CT成像基本原理

根据电磁波理论，电磁波传输过程中，耗散介质的初始场强E0与接收场强E关系为［7］：

其中，E是观测点接收到的场强（dB）；E0为初始场强（dB）；a为介质对电磁波吸收系数；r为收发点间距（m）；f（θ）为收发天线方向因子；θ为接收点处天线与电场方向夹角［8］。一般情况下E0值是未知的，且介质电磁参数变化较大时，E0值随位置而变化［9］。

将式（1）两边经过变换后取对数可以得到ar＝，写成离散化形式，得到第i个观测点的方程＝di，其中di＝，aj是第j（j＝1，2，3，……）个网格电磁波的吸收系数，rij是第i条射线在第j个网格中的射线长度，di是第i（i＝1，2，3，……）个观测点的观测值［10］。

假设R是n条电磁波射线在m个网格单元中的射线元组成的m×n维矩阵；X是电磁波吸收系数组成的矩阵，X＝（α1，α2，α3，α4，…，αn）T；D为接收场强的观测值，D＝（d1，d2，d3，d4，…，dn）T，则所有观测点的发射和接收之间得到的线性方程组可以写成：RX＝D，通过合适的迭代算法求解上述线性方程组，就能够得到两个钻孔间介质的吸收系数，进一步得到吸收系数的等值线图［11］。

解上述线性方程组的方法有很多［12］，比如共轭梯度法CG（Conjugate Gradient）、代数重建法ART（Algebraic Reconstruction Technique）、奇异值分解法SVD（Singular Value Decomposition）、联合迭代法SIRT（Simultaneous Iterative Reconstruction Technique）、最小二乘QR分解法LSQR（Least Squares QR－decomposition）等，不同方法的成像结果各有区别［13］。

3 影响相邻孔对数据不吻合的因素

从上述电磁波基本原理可以看出，影响电磁波CT成像误差的主要因素包括反演方法的选择和初始场强E0的处理。

3.1 反演方法的影响

反演方法包括算法本身和反演参数的设置。2019年赵威对电磁波CT几种常用的成像方法进行了对比分析［14］，确定SIRT是最合适的方法。实际工作中，同一个工作区相邻孔对的反演成像通常采用相同的反演算法，但反演参数的设置可能略有差别，因此下文中仅对反演参数的设置对相邻孔对成像误差的影响进行说明。

电磁波CT反演参数主要包括迭代次数、射线角度、初始模型等。参数较多，以迭代次数为例，建立一个简单吸收系数模型，如图1所示，模型中ZK1－ZK2、ZK2－ZK3为两对相邻孔对，ZK2为共用钻孔，模型背景值均设置为0.20Np／m，设置高吸收异常体和低吸收异常体各一处，大小为6m×4m，吸收系数分别为0.3Np／m、0.1Np／m，异常体中心深度分别为5m、15m。

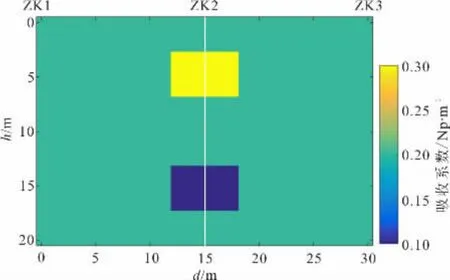
图1 吸收系数模型Fig.1 Model of the absorption coefficient

对上述模型中两对孔ZK1－ZK2、ZK2－ZK3分别采用SIRT法成像，除迭代次数外，其他反演参数均保持一致，提取成像结果中共用钻孔ZK2处反演数据，进行对比，计算相对误差。表1为该模型不同迭代次数成像结果在共用孔ZK2处的数据误差。

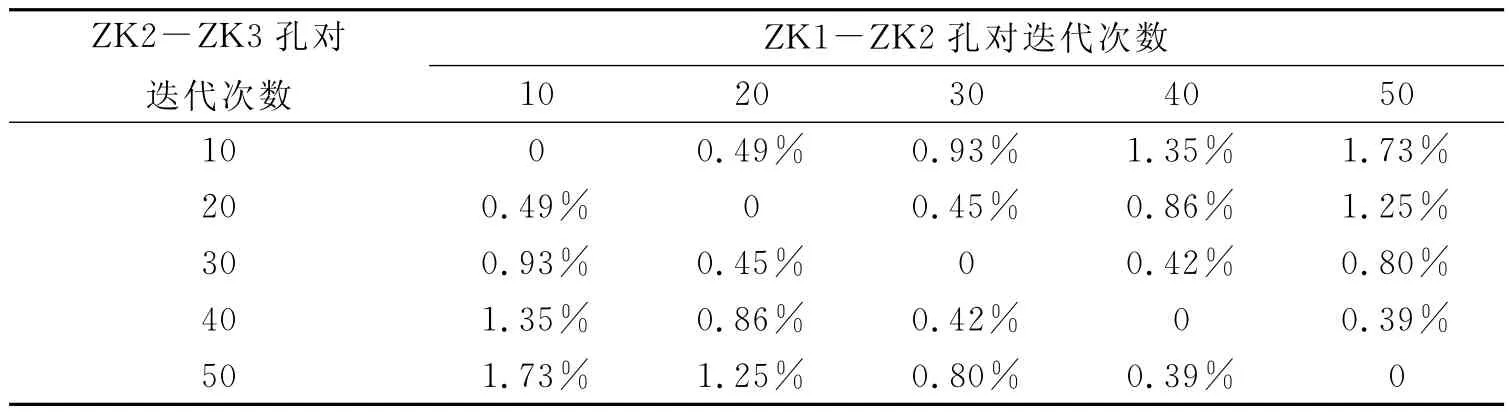
表1 共用孔处不同迭代次数相对误差（单位：%）Table 1 Relative error of different stacking times at shared holes（unit：%）

从表1中可以看出，理想情况下，反演参数完全相同时共用孔处数据的误差最小达到了0；随着迭代次数的增大，相对误差逐渐增大。实际工作中存在一些干扰，可能达不到理想的最小误差0，但总的来说，反演过程中统一反演方法和反演参数可以使相邻孔对在共用钻孔位置的误差最小。

3.2 初始场强E0的影响

在射线条件下，影响井间电磁波CT成像的因素中，E0值的确定是比较关键的问题，不仅因为E0是未知的，而且当介质电磁参数变化较大时，E0的值是随位置而不断变化的。张辉等［16］详细研究了初始场强对成像结果的重大影响，并进一步探究了该影响特征所呈现的规律性，得出不同场强会使成像结果形态不同。实际资料处理时，可以通过观察初始场强与反演结果之间的关系，从理论和经验两方面共同确定合理的初始场强值来部分消除对反演结果的影响，但如何准确获取各点的初始场强以得到更准确的反演结果，目前还没有一个比较成熟的方法。

4 相邻孔对的拼接

4.1 拼接思路

根据以上分析，相邻孔对共用钻孔位置的误差并不能从根本上完全消除，但是可以通过统一反演算法和反演参数、确定合理的初始场强值来最大限度地降低误差。

以贵州某岩溶勘查项目中电磁波CT既有数据为例，图2为两个相邻孔对各项反演参数进行统一、多次尝试确定初始场强的基础之上反演得到的成果图。从图2中可以看出，对于单对孔剖面而言，两个孔对的反演成果与实际钻孔均能吻合，但当两个孔对的反演数据直接进行拼接后，成图如图3（a）所示，在共用钻孔位置并不能较好地吻合，出现明显的等值线不连续现象。

图2 相邻孔对单孔等值线Fig.2 Contour map of adjacent holes versus single holes

图3 相邻孔对拼接效果Fig.3 Picture of adjacent hole pairs splicing effect

经过统计，勘查区内92对孔均与图3（a）中情况相似，对于单孔对而言，反演成果均能够跟实际钻孔吻合，但相互拼接时，却在共用孔位置出现明显的等值线不连续现象。按照上述情况，如果将两个相邻孔对在共用孔处的数据进行圆滑，而剖面其他位置的数据尽量保持不变，则可以实现相邻孔对的拼接，亦能够保证各剖面中异常不变。通过多次试验发现，采用反距离加权的局部多项式插值方式能够较好地实现相邻孔对的拼接，如图3（b）所示。

4.2 反距离加权的局部多项式插值法

局部多项式插值法是一种局部加权最小二乘拟合，根据有限个已知采样点数据，采用多个多项式来进行曲面的拟合，每一个插值点的预测值都对应一个多项式，利用局部多项式插值法得到的曲面，能够较好地描述短程变异；在一定区域内，不同采样点对内插点的影响不同，因此在计算多项式时，各点的权重也存在差异。通常情况下，临近区域内采样点的权重会随内差点与采样点之间的距离的增加而减小［17］，反距离加权法是目前最广泛采用的方法之一。

4.2.1 局部多项式插值方程

假设采样点的坐标为（xi，yi），其中（i＝1，2，…，n），内插点为N，坐标（XN，YN）为以N为原点建立局部坐标系，则（xi，yi）表示为［18］：

文中采用二次插值，由n个采样点的值可以得到方程组：

其中i＝1，2，…，n。写成矩阵形式为：

求解多项式系数矩阵，表达式如下：

通过最小二乘求解多项式系数：

式（9）中，P为每个采样点通过反距离加权法确定的权重，由此求得局部多项式插值方程，进而得到内插点的数值。

4.2.1 反距离加权法

反距离加权法用来反映不同采样点与内插点的相关程度，确定的原则与该数据点到内插点的距离di（i＝1，2，…，n）有关，di越大，数据点对内插点的影响越小，权重也越小，反之权重越大［19，20］。本文以距离平方的反比为权，权函数的表达式为：

其中，di为数据点到插值点的距离。

4.3 相邻孔对的拼接

以上述贵州岩溶勘查项目为例，电磁波CT钻孔孔对如图4所示，根据钻孔在平面上的位置关系，将92对钻孔划分为纵横交错的23条剖面，以下选择两种不同异常下的剖面拼接效果进行分析，一是团块状及不规格形状异常剖面的拼接（图5），二是近直立异常的剖面拼接（图6）。

图4 井间电磁波CT拼接剖面示意Fig.4 Schematic diagram of cross well electromagnetic wave CT splicing profile

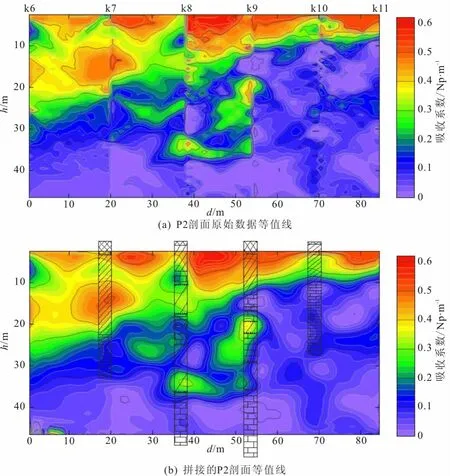
图5 P2剖面处理前后拼接等值线Fig.5 Splicing contour map before and after P2profile processing

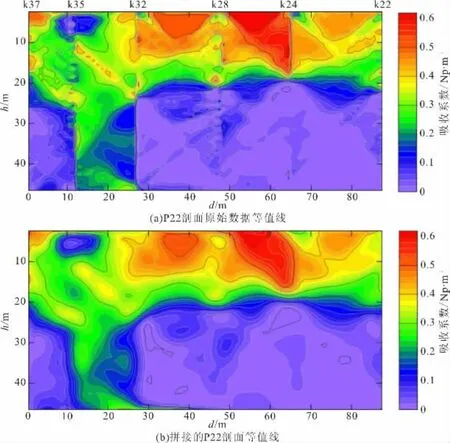
图6 P22剖面处理前后拼接等值线Fig.6 Splicing contour map before and after P22profile processing

图5（a）为P2剖面5对钻孔原始剖面数据拼接成图。由图5可以看出，整个剖面数据的整体水平基本一致，但是在k7、k8、k9、k10钻孔位置存在比较明显的吸收系数突变现象，图上等值线图连续，这种现象无法从地质上进行解释。图5（b）为经过反距离加权的局部多项式插值法处理后成图效果，通过对比可以看出，经处理后拼接的等值线变得圆滑，电磁波吸收系数异常的位置及大小均未发生明显变化，但各孔对拼接位置等值线不连续的现象消失，各孔对之间等值线过渡自然，且与实际钻孔情况吻合。

图6 为P 22剖面处理前后的等值线图。其中，图6（a）为P22剖面5对钻孔原始剖面数据拼接成图，图中K37－K35、K32－K28、K28－K24、K24－K22四对孔剖面数据的整体水平基本一致，但K35－K32孔对的数据较两侧都有很大的差异，该孔对在整个剖面中呈直立的异常存在；经过曲线拟合后数据成图如图6（b）所示，等值线变得圆滑，各孔对拼接位置等值线错断现象消失，但K35－K32孔对仍然保持近似直立的异常存在。

基于单孔来看，K35－K32剖面等值线形态与其他孔对的剖面形态区别不大，整体呈上高下低的趋势，只是在多孔对拼接在一个剖面中才会发现该孔较相邻两侧的异常。为了分析此类现象是否仅由剖面拼接而造成的虚假异常，笔者收集了全区存在类似异常的剖面，共5条，投影到平面位置上有明显的对应关系，详见图7。后期经过验证为地下暗河，边界与电磁波CT近直立异常一致（图8）。

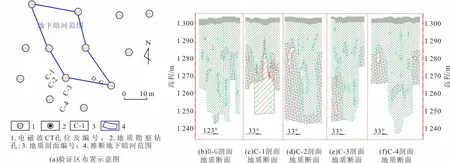
图8 验证地质剖面示意图Fig.8 Schematic diagram of verified geological profile

综上所述，采用反距离加权的局部多项式插值法对实测井间电磁波CT数据拼接是可行且有效的。

5 结论及讨论

5.1 结论

1）通过对反演方法、初始场强两个主要影响因素的分析认为，电磁波CT相邻孔对拼接误差受反演方法及初始场强的影响，并不能从根本上完全消除，但是可以通过统一反演算法、反演参数、多次试验确定合理的初始场强值来最大限度地降低误差。

2）目前常用的单孔对成像解释能够识别两个钻孔之间的大部分形态异常，通过反距离加权的局部多项式插值法进行拼接后的多孔对电磁波CT剖面，其结果与原单孔剖面的拟合度较高，在拼接图上，异常均能够完全遵循原始剖面的特征，共用孔处等值线连续、过渡自然，成像结果可信度高。

3）单孔对成像在综合成果解释时对近直立异常，特别是钻孔附近的直立异常无法识别，通过反距离加权的局部多项式插值法进行拼接处理，可以准确识别单孔对无法识别的近直立异常，同时多个剖面综合解释还可以准确识别跨越多个孔对，有一定跨度的水平异常，对提高电磁波CT成果解释具有实际应用价值。

5.2 讨论

影响多孔对电磁波CT剖面拼接的因素是复杂的，目前尚没有成熟的解决方法，这些难题都需要在以后的工作中进一步深入研究。本文多孔对电磁波CT剖面拼接是基于既有单孔对反演的成果数据进行的，各单孔对经反演参数统一和合理初始场强反演后，整体背景相差不大，且单孔对反演成果均能够跟实际钻孔吻合，采用反距离加权的局部多项式插值法拼接能够达到理想的拼接效果，在此基础上亦可以尝试将拼接后的数据赋予三维空间位置坐标，然后采用三维成像软件进行成像，结合三维切片初步实现三维展示。