时空域与τ—p域预测反褶积压制多次波方法对比研究

席自彬，麻志国，王海昆，徐 强

（中海油田服务股份有限公司物探事业部，天津 300451）

1 引言

多次波的产生需要良好的反射界面，只有在反射系数较大的反射界面上产生的多次反射，才能形成较强的多次波，并被检波器记录下来［1］。由于海洋地震资料采集特性，海水—空气、海水—海底都是良好的反射界面，所以海洋地震资料中多次波比较发育。常见的海上地震资料中，既有在海水与海底之间多次震荡产生的鸣震、交混回响等多次波，又有由于海水横向深度变化剧烈（尤其深水）产生的绕射多次波，以及层间多次波等［2，3］。因此，对于海洋地震资料，关于多次波的去除是一项重要的工作。目前，去除多次波的方法有多种。基于滤波类的多次波去除方法［4，5］依据的是一次波与多次波信号特征上的差异，即周期性差异或者速度性差异；基于波动方程的多次波预测方法［6－8］是从波场的角度预测，并从原始地震记录中减去多次波。

预测反褶积方法是工业生产中常用的多次波压制方法，它是滤波类多次波去除方法的一种。该方法主要根据多次波在时间上呈现的规律性，不需要速度等辅助信息，同时预测步长又可以通过自相关或者步长扫描得到，兼具参数设置简单和运行速度快的特点。预测反褶积方法自1954年Robinson首次提出以后［9］，经历了几十年的发展与演进，已成为地震资料处理中最基本、最常规的处理手段［10－12］。唐博文等［13］等于2010年在频率域设计提出一种新的谱模拟反褶积方法，该方法可以在不做多项式拟合时准确提取子波振幅谱。2015年，王元君等［14］在动态褶积模型基础上，提出一种基于时频域的动态反褶积方法，该方法是基于S变换的变Q值情形估算反射系数来提高地震资料信噪比。2021年，张联海等［15］研究了基于深度卷积神经网络的稀疏反褶积方法，该方法可以不用多次设置参数来提高计算的速度和精度。上述研究方法主要是通过不同反褶积方法求取地震反射系数及提高地震分辨率，对反褶积方法压制多次波没有进行深入的探讨。在预测反褶积压制多次波研究方面，2015年，徐云霞等［16］研究了f—x域预测反褶积在共偏移距衰减多次波；2018年，张红梅［17］将线性拉东域预测反褶积方法应用于海上地震资料处理；张向辉［18］将该方法推广应用到陆上复杂地质成像中，均取得了较好的多次波压制效果；何林帮等［19］提出双曲Radon域预测反褶积方法，该方法可以压制速度逆转的多次波及中长期多次波，缺点是局部存在损失有效信号现象。但是上述研究方法更偏向于实际资料处理，对压制多次波时影响参数和保幅性等问题没有进行深入的研究。时空域与τ—p域预测反褶积是目前工业生产中普遍使用且较为成熟的反褶积方法，相较其他方法，具有参数设置简便、计算速度快及计算精度高的优点。本文首先阐述了时空域预测反褶积和τ—p域预测反褶积方法的基本原理，分析了两种方法的影响参数、频谱特性，同时分析了两种方法的相对保幅性质，在实际海洋地震资料处理中分析两种方法的优缺点。大量实际资料证明，预测反褶积方法在消除海上地震资料中虚反射、交混回响、鸣震或者其他形式简单的多次波方面有较好的效果。

2 预测反褶积方法原理

2.1 时空域预测反褶积基本原理

在实际地震勘探中，一次反射波对应着实际地层，在同一点不同的时间，一次反射波基本上是不同的，没有规律性，即它在时间上不可预测。对于鸣震等多次波，它在地震剖面上出现的时间有规律性，即可以通过前面的波形预测出后面的波形。从地震记录中减去多次波干扰，得到一次波反射，即为预测误差。假设地震子波a（t）为最小相位子波，反射系数ξ（t）为白噪声，则褶积模型定义为：

t＋l时刻的输出为：

而预测误差为：

从式（3）可以看出，式（2）中第二项为预测值x＾（t＋l）（多次波），第一项为预测误差e（t＋l）（一次波）。因此，

若设a′（t）＝（a（0），a（1），…，a（l－1）），即取地震子波的前部，则式（4）变为：

式（5）说明：预测误差为反射系数和子波前部进行褶积处理，这也是预测反褶积方法能够压缩子波长度的本质，从而达到提高纵向分辨率的目的。从子波角度看，预测反褶积相当于对子波进行截尾处理，截取子波为a′（t）＝（a（0），a（1），…，a（l－1））。

下面求取预测因子和反褶积因子。众所周知，预测反褶积是维纳滤波，即基于线性预测理论的最小平方滤波。假设b（t）＝（b（0），b（1），…，b（m））为预测因子，则在最小平方情况下，可推出求解预测因子的方程：

式（6）中，rxx为地震记录的自相关；λ为白噪系数。计算出预测因子后，通过和地震记录褶积得到预测值，再由式（3）得到去噪结果。

2.2 τ—p域预测反褶积基本原理

τ—p域预测反褶积也就是线性Rodon域预测反褶积，它的实现需要经过三个步骤：首先是将时空域（t－x域）道集经过线性Rodon变换转换到τ—p域（Rodon域也称慢度—截距时间域）；第二步，在τ—p域对每一个慢度道做预测反褶积，去除多次波；第三步，经过线性Rodon反变换转换到时空域，得到去除了多次波的地震记录［20］。

由地震反射理论可知，

而射线参数p为：

所以由式（7）和式（8）可得：

即

式（7）～式（10）中：x为偏移距（m）；t为双程旅行时（s）；t0为垂直反射时间（s）；v为介质速度（m／s）；p为射线参数；τ为p＝0时的截距时间。通过式（10）进行时空域和τ—p域互相转换。假设时空域的道集为f（x，t），F（τ，p）是时空域道集的Rodon变换，n为τ—p变换所参与运算的道数，则将时空域道集经式（10）转换到τ—p域，可得

然后在τ—p域进行预测反褶积，过程和时空域预测反褶积原理一样，将周期性的多次波去除，得到τ—p域衰减多次波后的一次波记录Fa（τ，p），然后由式（10）进行线性Rodon反变换，得到时空域衰减多次波后的一次波fa（x，t），即

由图1可以看出，对于同一个p值，信号虽然可以在很多偏移距接收到，但却对应着同一个入射角，因此多次波有着严格的周期性，多次波的周期不会受到偏移距变化的影响，这也是τ—p域多次波周期性好于时空域多次波周期性的根本原因。

图2 主要展示道集在时空域和τ—p域之间的相互映射关系。由式（10）可以知道，直达波B（图中经过原点直线）转换到τ—p域就是一个点B′。对于入射角小于临界角的折射波A（图中截距不为0的直线）和反射D，转换到τ—p域为低P值区A′和D′。而对于宽角反射C，则映射到高p值区C′［21］。

图2 时空域道集和τ—p域道集的相互映射关系Fig.2 Mapping relationship between temporal spatial gather andτ—pgather

3 影响参数分析

3.1 时空域预测反褶积影响参数

3.1.1 预测步长的影响

图3为水平水层多次波模型。由图3可知，在时空域，低一阶次与高一阶次反射波时距关系为：

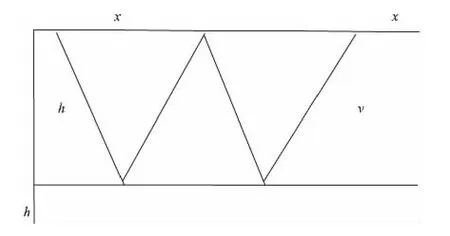
图3 水平水层多次波模型Fig.3 Multiple wave model of horizontal water layer

式（13）中，n为表面多次波的阶数；h为激发点处的法向深度（m）。当x＝0时，有Δtn＝。因此在时空域（t－x域），只有在零炮检距记录即垂直入射（x＝0）的情况下，多次波才有严格的周期性。随着多次波偏移距的增大和深度的加深，多次波的时差会减小，即多次波在时空域是时空变的。因此，在实际处理中选取预测步长时，如果预测步长取值过小，不能准确预测并有效去除多次波；而且不能以近道的自相关次极值为标准，要以远道的自相关次极值为参照，才能有效地去除整个道集的多次波。

3.1.2 算子长度的影响

算子长度较易求取，在式（6）中，只要满足自相关中包括多次波和一次波的主要能量，算子长度就能满足预测反褶积的要求。但是，算子长度必须大于多次波的一个周期，如果预测算子长度太小，可能会带来假的能量。在实际处理中，可以适当地给大算子长度，对结果没有影响。

3.2 τ—p域预测反褶积影响参数

由于τ—p域预测反褶积包括τ—p正、反变换和预测反褶积两大步，因此影响因素也要充分考虑这两方面参数的影响。对于理论模型，τ—p域预测反褶积可以很理想地去除多次波，但是受采集方式和海底复杂情况的影响，实际情况非常复杂。

3.2.1 算子本身的影响

从式（7）和式（11）可以看出，由于公式近似和数值离散造成空间采样率不足，会在τ—p正、反变换过程中带来假频。为有效防止空间假频，已知道间距Δx时，可知最大波数k为，进一步推导最大慢度pmax为：

为有效防止慢度p上的假频，在已知偏移距范围xr和最大频率fmax的情况下，必须满足相邻p道间的时差小于一个周期（T），所以有

为有效防止截距时间τ上的假频，可以与时间采样定理一致，须满足：

3.2.2 参数pmax的影响

一个入射角对应一个射线参数p，同时对应着τ—p域一道；pmax既对应资料中最大倾角，也对应τ—p域的最大道数。若pmax过大，即在时空域道集上并不存在与之对应的同相轴，会在τ—p域相应道上产生噪音。产生的噪音也会参与预测反褶积运算，然后通过τ—p反变换转换到时空域，会在τ—p反变换后的时空域道集上带来噪音，造成道集信噪比下降。因此，pmax应选择地震资料中处理感兴趣的倾角范围，不应过大。

3.2.3 其他因素的影响

1）直达波以及折射波对τ—p域预测反褶积有影响，由式（10）知，直达波以及折射波转换到τ—p域是一个点，不能准确地再转换回时空域，所以在做τ—p域预测反褶积时，需要切除直达波和折射波，或做相应特殊处理；

2）关于τ—p域采样psample，当采样不足时，会产生一些随机噪音，但是过采样不会产生任何影响，也不会提高道集的质量；

3）关于最大频率Fmax，主要用于计算p的道数，必须给足，但是大小不会影响道集的质量，过大会影响计算的效率。

4 保幅性分析

假设时空域道集上两道地震记录为x1（t）和x2（t），首先经过地表一致性处理，消除道集的子波横向性差异，在此基础上，假设两个地震记录振幅在时窗t1～t2时刻内任意采样点满足x2（t）＝kx1（t），其中k为任意常数，预测反褶积后，相应的地震记录为y1（t）和y2（t），b1（t）和b2（t）为相应的预测反褶积算子，则最小平方反褶积滤波方程为式（6）。假设rxx为地震记录的自相关，由于rxx（τ）＝，可得rx2x2（τ）＝k2rx1x1（τ），其中，τ＝0，1，…，m。因此，式（6）左边自相关矩阵满足R2＝k2R1。当l为预测步长时，预测反褶积可以将rxx（l＋τ）当作rdw（τ）。因此可得，rx2x2（l＋τ）＝k2rx1x1（l＋τ），所以可得b1（t）＝b2（t），则预测值满足y′2（t）＝ky′1（t），最终可求得反褶积后的振幅值y2（t）＝ky1（t），即预测反褶积前后的振幅比例没有变化，所以单道的预测反褶积是相对保幅的。

对于多道预测反褶积来说相对简单，由于相邻多道采用相同的反褶积因子，即b1（t）＝b2（t），又因为x2（t）＝kx1（t），由反褶积运算可得y2（t）＝ky1（t），所以多道预测反褶积也是相对保幅的。在预测反褶积运算中，使用较多的是多道预测反褶积，因为多道预测反褶积统计误差小，子波提取比单道预测反褶积稳定，所以相对保幅性要好于单道预测反褶积［22，23］。本文采用的就是多道预测反褶积方法。

5 实际海上资料处理应用

本文选择渤海某工区实际资料，首先对τ—p域预测反褶积影响参数进行数据测试，然后分别在时空域和τ—p域做预测反褶积，对比反褶积效果。

5.1 τ—p域预测反褶积影响参数数据测试

5.1.1 算子本身的影响

由于计算公式采取近似和数值离散造成采样率不足，会在τ—p正、反变换过程中带来假频。如图4所示，图4（a）为原始炮集，4（b）为经过τ—p正、反变换后的炮集，图4（c）为τ—p正、反变换带来的假频。

图4 τ—p正、反变换前后效果Fig.4 Effect before and afterτ—pForward and reverse transform

5.1.2 参数pmax的影响

如图5所示，最大道数pmax过大时，会在τ—p正变换后产生噪音。从图6可以看出，产生的噪音也会参与预测反褶积运算，然后通过τ—p反变换转换到时空域，会在时空域道集上形成噪音，造成道集信噪比下降。因此，对于pmax的大小应选择地震资料中处理感兴趣的倾角范围，不应过大。由式（14）可知，pmax取值应小于。

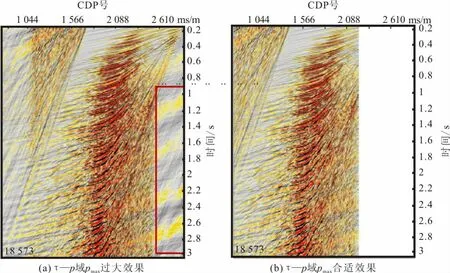
图5 τ—p域不同pmax大小效果Fig.5 Different pmaxeffect inτ—pdomain

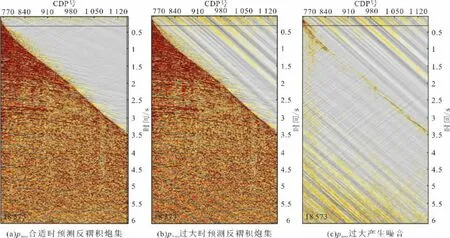
图6 不同pmax值时τ—p域预测反褶积效果Fig.6 Predictive deconvolution effect with different pmaxinτ—pdomain

5.2 两种预测反褶积方法实际数据测试对比

图7 为原始炮集，图8为时空域原始炮集的自相关和预测反褶积后的自相关，选取的时窗为1600～3200ms。从自相关上可以看到，时空域近偏移距多次波去除效果较好，但是在远偏移距上还有少许残留的多次波。图9为原始炮集τ—p域自相关和τ—p域预测反褶积后的自相关，选取时窗和时空域相同。从图9可以看出，τ—p域预测反褶积多次波去除效果比时空域好，但是带来了一些低频噪音。图10为预测反褶积前（红色）、时空域预测反褶积（绿色）、τ—p域预测反褶积（蓝色）三者频谱对比，选取的时窗为500～2000ms。从图10可以看出，τ—p域预测反褶积优势频带更宽，高频成分、低频成分更丰富。图11为预测反褶积前（红色）、时空域预测反褶积（绿色）、τ—p域预测反褶积（蓝色）三者振幅谱对比。从图11可以看出，预测反褶积方法相对保幅，时空域预测反褶积振幅值约是τ—p域预测反褶积振幅值的1.2倍，因此，时空域预测反褶积相对保幅效果更好。由于τ—p域预测反褶积的实现要经过τ—p域正、反变换和预测反褶积两步，因此它的计算效率要低于时空域预测反褶积。实验证明，τ—p域预测反褶积计算时间是时空域预测反褶积的1.5倍。

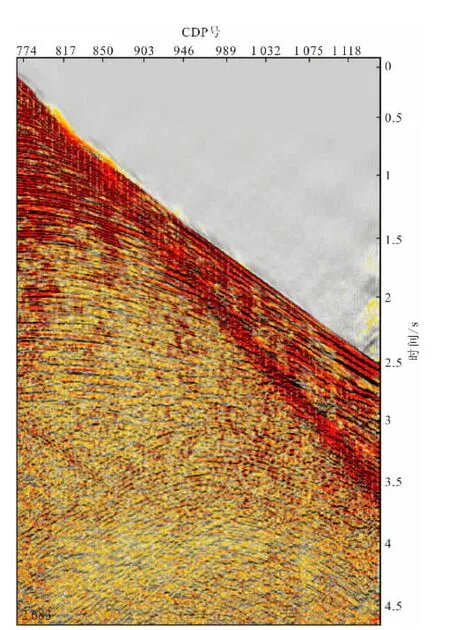
图7 原始炮集Fig.7 Original shot gather

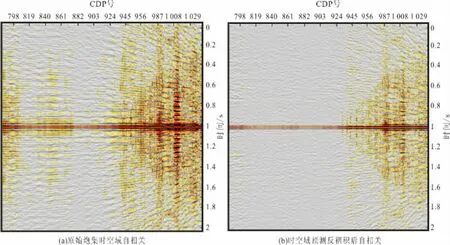
图8 时空域预测反褶积前后炮集自相关Fig.8 Shot gather auto－correlation before and after temporal spatial predictive deconvolution

图9 τ—p域预测反褶积前后炮集自相关Fig.9 Shot gather auto－correlation before and afterτ—pdomain predictive deconvolution

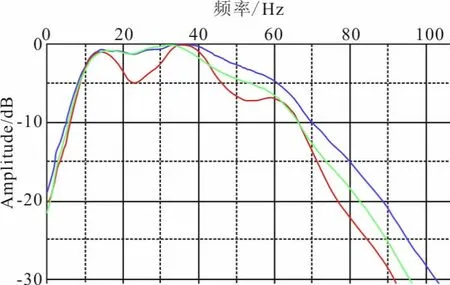
图10 不同反褶积方法频率谱Fig.10 Frequency spectra of different deconvolution methods

图11 不同反褶积方法振幅谱Fig.11 Amplitude spectra of different deconvolution methods

在两种预测反褶积均采用最优参数的情况下，对比两种预测反褶积效果。从图12叠加剖面可以看出，时空域预测反褶积多次波有少许残留（图中黑色箭头位置），τ—p域预测反褶积对多次波压制更干净。但在相对保幅性方面，时空域预测反褶积叠加剖面同向轴更实，连续性更好（图中绿色箭头位置），保幅效果要优于τ—p域预测反褶积。

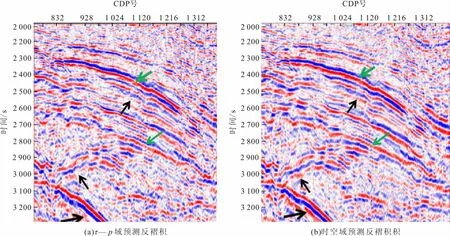
图12 两种预测反褶积叠加效果对比Fig.12 Comparison of two predicted deconvolution stack effects

6 结论

时空域和τ—p域预测反褶积在实际资料处理时存在明显差别：时空域预测反褶积主要受预测步长和算子长度两项参数影响较大，在实际处理中选取预测步长过小时，不能准确预测并有效去除多次波。算子长度也必须大于多次波的一个周期，预测算子长度太小，会带来假的能量。相比而言，多次波在τ—p域有更明显的规律性，但是由于该方法本身在计算时存在公式近似和数值离散，会在τ—p正、反变换过程中因空间采用率不足带来假频。并且pmax参数的选择至关重要，需要经过反复实验论证，数值太小会造成有效波缺失，数值太大会带来假的噪音。同时，τ—p域预测反褶积还需要关注直达波、折射波、τ—p域采样间隔、最大频率等参数的影响，因此在实际处理时更加需要精细对待。通过本文的对比研究，可以得到以下几个结论：

1）在时空域，多次波只有在垂直入射即零炮检距情况下才能保持其周期性，但是在τ—p域，多次波具有严格的周期性，不随炮检距变化而变化，所以在τ—p域去除多次波效果更理想；

2）τ—p域预测反褶积去除多次波效果优于时空域预测反褶积，同时可以拓宽优势频带，丰富低频、高频信息；

3）预测反褶积方法是相对保幅的，时空域预测反褶积相对保幅性效果要优于τ—p域预测反褶积，同时时空域预测反褶积的计算效率是τ—p域预测反褶积的1.5倍。