车齿工艺主切削力预测与工艺参数优化*
2023-11-15阳国万温子进陈永鹏
阳国万 温子进 陈永鹏
(重庆交通大学机电与车辆工程学院,重庆 400074)
车齿工艺是一种加工效率高、加工精度高,适用于传统齿轮加工方法难以加工的特殊结构(如非贯通内斜齿轮)的新型齿轮制造工艺,最初由于落后的技术条件而未能在实际工业生产中得到广泛应用,但如今随着一些关键技术——机床刚度、计算机数字控制、材料涂层技术等发展,车齿工艺所展现出的巨大潜力引起了学界内更多的关注。
在齿轮切削加工过程中,所产生的切削力是齿轮制造工艺最基本的物理参数,掌握切削力的变化规律是研究切削机理、研发新型刀具、提高加工精度的关键与前提,国内外众多学者对此展开了广泛研究。Tang X K 等[1]针对铣削所产生的切削力,提出了三维未变形切屑厚度的计算方法,得到了穿透曲线的计算公式以确定加工区域,通过矢量分析法确定了工作法前角与工作刃倾角,最后建立了切削力力学模型以预测铣削力。Jiang C 等[2]认为切削力是影响刀具寿命和机床加工性能的重要因素,根据展成法加工准双曲面齿轮的特点与实际工况,提出了一种计算多齿切向铣削力的新方法,并根据刀具与工件之间的运动和位置关系,计算出了动态切向铣削力,最后通过实例计算与实验对比验证了模型的准确性。Zheng F Y 等[3]为了解决面铣削加工螺旋锥齿轮时复杂运动学所导致的预测切削力的难题,提出了一种高效、准确的面铣螺旋锥齿轮切削力解析预测模型,通过有限元模拟和切削力实验验证了该方法的有效性,切削力误差在10%以内。Chara E等[4]开发了一种实现面铣削和面滚削的三维运动学仿真计算算法,可以计算切削过程中的切削力,进而研究了精加工余量、进给速率等关键参数对未变形切屑几何形状与切削力的影响。蔡安江等[5]基于金属切削力理论公式剃齿切削力模型,分析了切削参数对剃齿切削力的影响规律,运用有限元方法与试验结果进行了对比验证了模型的准确性。Huang K F等[6]主要研究了准双曲面齿轮面滚齿切削力预测的向量化封闭解,建立了未变形切削切屑几何形状的矢量化模型,将该模型与斜角切削模型结合首次提出了准双曲面齿轮面滚齿切削力预测的封闭解,该模型与半解析法相比具有更高的精度与效率。Jin Y Q等[7]依据实际工况建立了多齿切削过程切削力的有限元数值分析模型,在此基础上进一步研究了瞬时切削力的时变特性,探讨了切削参数对切削力的影响规律,最后结合切削试验结果,对稳态切削力进行了比较,验证了模型的可靠性。Onozuka H 等[8]以提高车齿工艺加工精度和刀具寿命为目标,建立了切削力的仿真模型,利用可以代表工件材料切削力特征的切削方向、未变形切屑厚度、有效前角和特定切削力系数来表示切削力,并采用优化方法减小实测切削力和模拟切削力的误差,二者之间具有较好的吻合性,误差为15%。McCloskey P 等[9]介绍了一种新型模型,用于预测高速、多功能齿轮切削过程中未变形切屑的几何形状与切削力,计算了离散化切削刃的切削速度,确定了有效前角与斜角,最后利用DMG 铣床进行了实验验证。Li J 等[10]提出了一种基于能量法的车齿工艺切削力计算方法,该方法将刀齿上的切削刃分为切入刃、顶刃和切出刃3 个部分,将切削刃3 个部分上每一微段的切削力矢量相加,得到单齿上的切削力,这样便得到由参与切削的刀齿上切削力矢量和的完整切削力,最后通过有限元方法验证了该方法的有效性。Svahn M 等[11]用力学方法建立了一个数学模型以对齿轮成形铣削过程中的切削力进行预测,该模型认为在切削过程中刀具上的载荷都是通过沿切削刃的力之和求解的,最后用转位铣刀进行了实验,验证了该模型能较好地预测铣削力。
早期关于齿轮制造工艺切削力的研究多集中于传统齿轮制造工艺,虽然近年来逐渐出现了一些关于车齿工艺切削力的探究,但仍然不全面且不深入,对车齿工艺切削力的预测与优化是难题之一。针对上述问题,本文建立了工件齿轮和车齿刀的三维模型,基于Deform 有限元仿真得到了单刀齿切削过程中切削力的响应数据;建立了多元参数作用下主切削力预测模型,分析了切削速度、进给量以及轴交角三项工艺参数对主切削力的影响规律;提出了以主切削力为约束条件、以最高加工效率为目标的工艺参数优化方法,并验证了预测模型有效性,为提高车齿工艺加工效率、延长刀具寿命提供参数指导。
1 车齿工艺运动学原理
车齿工艺是基于空间交错轴圆柱齿轮啮合原理的齿轮加工工艺,车齿工艺运动学原理如图1 所示。
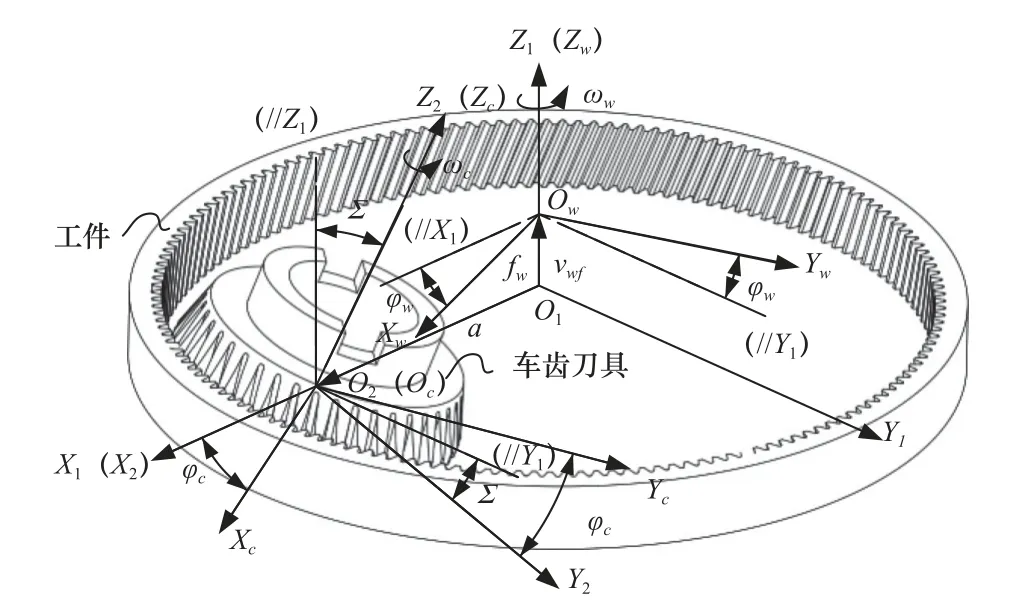
图1 车齿工艺运动学原理
根据车齿工艺运动学关系构建车齿工艺空间坐标系:坐标系S1(O1-X1Y1Z1)与坐标系S2(O2-X2Y2Z2)为固定坐标系,分别与工件与刀具起始位置重合;固定坐标系Z1轴与Z2轴分别同工件与刀具的轴线重合;坐标系Sc(Oc-XcYcZc)与坐标系Sw(Ow-XwYwZw)分别为刀具与工件的固连坐标系,并且刀具与工件分别绕着Zc轴与Zw轴以角速度ωc与ωw做同步回转运动,同时工件以速度vwf做轴向进给运动。
Z1轴与Z2轴间最小距离为中心距a,满足:
式中:车齿加工外齿轮时取正号,车齿加工内齿轮时取负号;rw为工件分度圆柱半径;rc为刀具分度圆柱半径。
Z1轴与Z2轴间交错角为轴交角Σ,满足:
式中:车齿加工外齿轮时,若刀具与工件螺旋方向相同则取正号,若刀具与工件螺旋方向相反则取负号;车齿加工内齿轮时,若刀具与工件螺旋方向相同则取负号,若刀具与工件螺旋方向相反则取正号;βw为工件螺旋角;βc为刀具螺旋角。
为了满足车齿工艺刀具与工件之间正确啮合关系,应给刀具附加差动回转运动,则刀具角速度ωc与工件角速度ωw之间关系为
式中:zw为工件齿数;zc为刀具齿数;mwn为工件法向模数。
根据式(3)可确定刀具回转角度φc与工件回转角度φw之间的关系为
2 车齿工艺有限元仿真
车齿加工是一个复杂的动态过程,其切削结果受众多因素影响,碍于现有技术,测量车齿加工过程中切削力往往不精确,并且实验成本巨大,这些难题大大延长了车齿工艺研究开发周期。为了解决上述问题,有限元方法因其效率高、成本低、便于监测全程等优点而受到越来越多青睐,本文选用DEFORM-3D 有限元平台对车齿加工过程中切削力进行分析。
2.1 几何建模与划分网格
在保证仿真结果准确的前提下,应尽量简化仿真模型,本文选取刀具单刀齿及相应齿槽模型而非完整刀具与工件进行切削仿真。
几何建模与网格划分方法如下:
(1)根据表1 的刀具与工件设计参数构建其刀齿几何模型,如图2 所示。

表1 刀具与工件设计参数

图2 刀齿几何模型
(2)基于车齿工艺运动学原理,利用切削刃运动轨迹构建对应的齿槽几何模型,如图3 所示。

图3 齿槽几何建模过程
(3)由式(1)~式(3)计算出的工艺参数装配刀具与工件,如图4 所示。
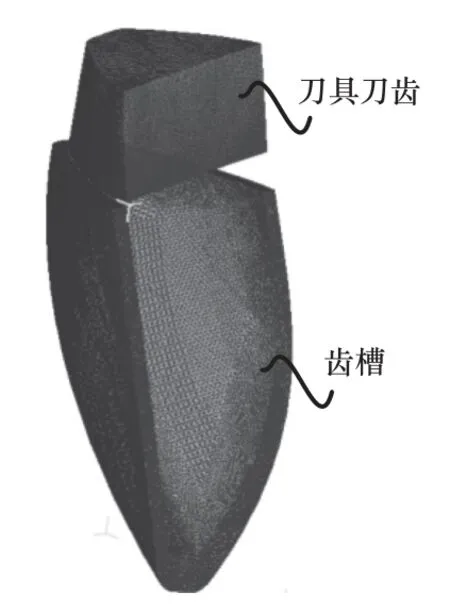
图4 装配与网格
(4)刀齿与齿槽默认划分为四面体网格,网格数分别约为430 000 与80 000,并针对前刀面设置网格窗使窗内网格体积更小,窗内外网格体积比为0.01∶1,刀具涂层材料为5 µm TiAl。
2.2 材料本构模型及断裂准则
金属切削过程中会产生较大塑性形变,工件材料会出现加工硬化现象,Johnson-Cook 模型被广泛应用于模拟金属切削过程,对模拟高应变和高应变率的机械过程非常有效[12],十分适用于车齿加工仿真,该模型屈服应力方程为
材料模型各参数见表2。

表2 材料模型参数
由于合金结构钢25CrMo4 切削性能良好[13],因此合金工具钢AISI-H-13(即4Cr5MoSiV1)被广泛用于制造刀具[14],本文分别选用25CrMo4 与AISI-H-13为工件与刀具的材料。
现有预测挤压裂缝起裂标准中,Cockcroft &Latham 准则是最常用的准则[15],本文断裂准则采用该准则,其临界损伤值具体形式为
式中:εf为临界断裂等效应变;σ为等效应力;f(σ)为等效应力函数;ε为等效应变。
3 主切削力预测及工艺参数影响分析
由于在车齿加工过程中切削力的大小与方向是不断变化的,因此目前还未统一切削力的计算方式。通过对车齿过程中作用力的分析,将任意时刻的切削力在工件固定坐标系S1(O1-X1Y1Z1)分解成3 个方向的分力,如图5 所示。与工件旋转方向ωw相互垂直(即与Z1轴同向)的力Fz为主切削力,与X1轴同向的力Fx为背向力,与Y1轴同向的力Fy为进给力,则切削力Fgs的表达式为
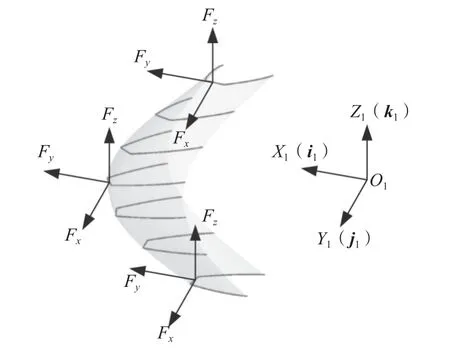
图5 切削力分解
与其他两向分力相比,主切削力Fz数值上非常接近总切削力,起主导作用,因此,本文将主要对主切削力进行预测与优化。
3.1 基于BBD 的仿真试验设计
Box-Behnken Design(BBD)是通过对响应面模型进行优化,而得到最优响应值的一种实验设计方法[16]。基于此设计方法,将3 个对切削力有影响的工艺参数(切削速度、轴向进给量以及轴交角)设置为实验因素,根据三因素三水平BBD 实验重复原则,进行17 组仿真实验,可得不同工况下车齿工艺切削力变化趋势。为了尽可能地控制切削力波动幅度,选择对切削过程中主切削力极值进行分析,结果见表3。l1、l2、l3分别表示切削速度、进给量与轴交角的设计水平。

表3 主切削力结果
图6 所示为序号1 实验三向切削分力在切削过程中的变化趋势,背向力Fx小于进给力Fy,且远远小于主切削力Fz,这就是设计新刀具、研发新机床、计算功率时将主切削力视为最关键因素的原因,证明了本文选择主切削力为研究对象的正确性。

图6 车齿加工过程中切削力变化趋势(序号1)
3.2 主切削力预测模型
为深入探究车齿切削速度、轴向进给量和轴交角3 个参数对主切削力的影响规律,建立了二阶预测模型,其表达式为
式中:w0为响应均值;wi(i为1~n的整数)为线性响应系数;wij(j为1~n的整数,但与i不相等)为双因素交互响应系数;wii为二次响应系数;ε为误差补偿。
式(8)中n的取值由因素数量决定,取值为3,故预测模型的具体形式应为
为准确地表达工艺参数对主切削力的影响规律,必须对式(9)进行误差补偿修正,修正后的结果为
最后,将表2 中各参数条件下主切削力结果代入式(10),可得本文主切削力预测模型,为:
对该模型进行方差分析,结果见表4。表4 中,F表示模型显著性;P表示模型显著性水平。标准F值为3.02,而本文中模型F值为20.44,远大于标准值;并且本文模型显著性水平P值为0.000 3,远小于置信系数0.05,进一步说明本文预测模型置信性高;此外,R2值0.963 3 与修正决定系数Adjusted-R2值0.916 2 非常接近,说明模型拟合度非常高。
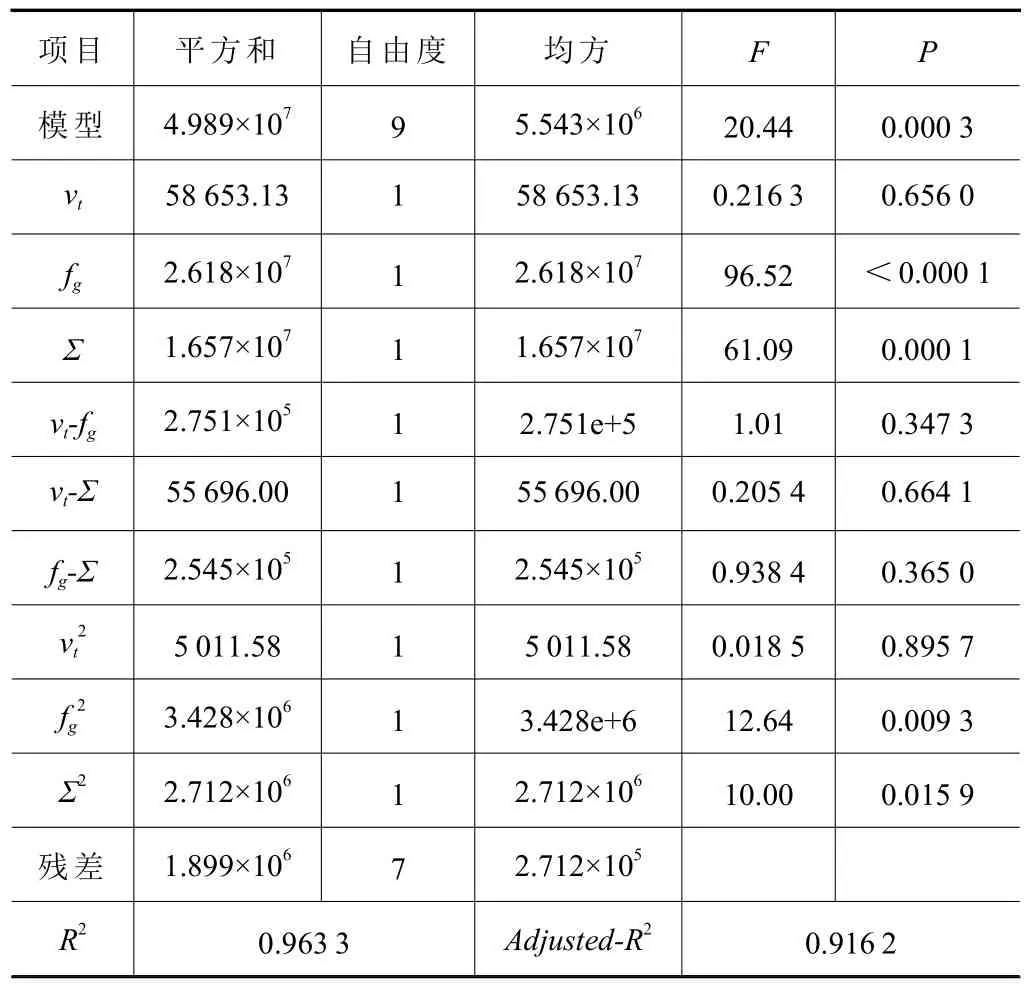
表4 主切削力预测模型的方差分析结果
3.3 单工艺参数对于主切削力的影响分析
为研究单工艺参数对主切削力的影响规律,根据数学预测模型构建其子模型,进而得到主切削力关于单工艺参数的边际方程,通过边际方程分析单工艺参数对主切削力的影响规律。
工艺参数使用无量纲转换后进行数学建模,一次响应系数wi、交互响应系数wij和二次响应系数wii之间线性不相关[17],令其中两项工艺参数水平为0,可得目标工艺参数对主切削力的数学预测子模型:
对式(12)中l1、l2、l3分别求导,可得主切削力的边际方程:
由图7 可知,在选定的工艺参数范围内,随着进给量的增大,主切削力也不断提高,这是因为进给量的增大导致切削厚度增加,刀具需克服的弹塑性阻力增大,并且进给量的参数水平越高影响主切削力的程度也越明显;轴交角的增大对主切削力的影响规律为先降低后提升,因此选用大轴交角会使切削力对刀具磨损的影响程度降低;切削速度的提高也会使主切削力增大,其原因为高切削速度使得刀具实际前角变小、变形系数增大继而导致切削力增大,但变化幅度不显著,并且随着切削速度参数水平的上升,因刀具积屑瘤的产生,从而引起主切削力受切削速度影响降低的问题。综上所述,单工艺参数对车齿工艺主切削力影响程度顺序为:进给量 >轴交角> 切削速度。

图7 主切削力边际方程
3.4 多元工艺参数对主切削力的交互影响分析
本节通过响应曲面图,分析多元工艺参数对主切削力的交互影响,具体方法:设置某一工艺参数水平为0 作参考,讨论另外两项工艺参数间交互作用对主切削力的影响规律。主切削力与工艺参数间响应关系如图8 所示。
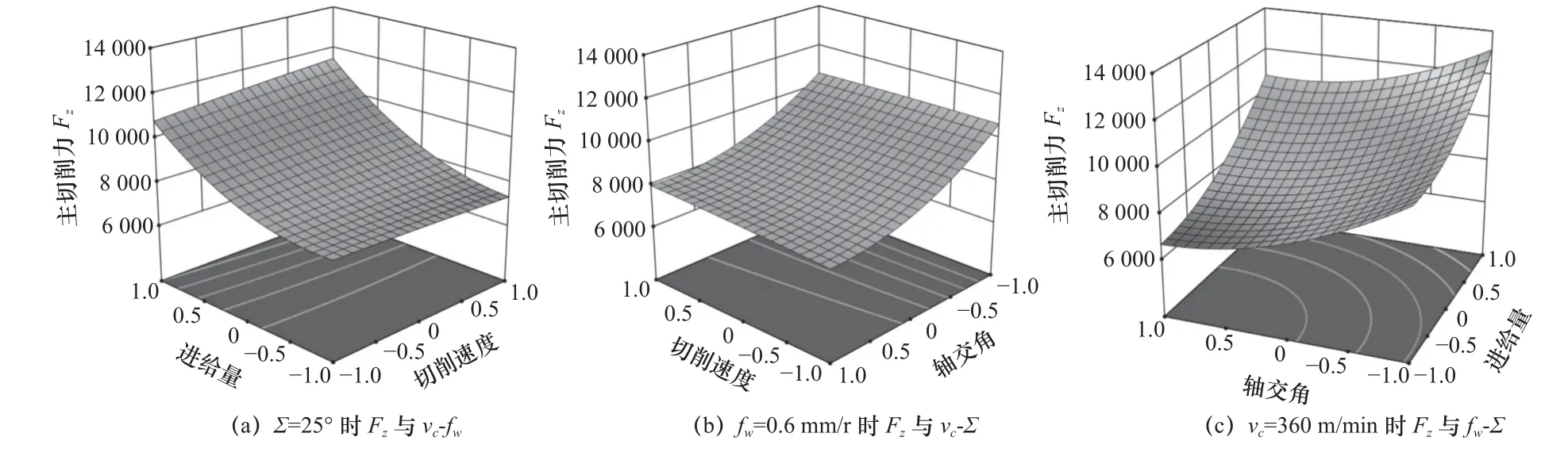
图8 主切削力与工艺参数之间的响应关系
由图8a 可知,随着进给量的增大,主切削力也不断增大,并且随着切削速度的提升,等高线就越陡峭,说明切削速度促进了进给量对主切削力的影响。由图8b 可知,随着轴交角的增大,主切削力不断减小,并且随着切削速度的提升,等高线就越平缓,意味着切削速度抑制了轴交角对主切削力的影响。由图8c 可知,轴交角与进给量对主切削力的交互影响规律呈辐射状,即轴交角越小、进给量越大,主切削力越大,并且两者对主切削力的影响程度较为相似。
通过在中寻找最高点与最低点发现:最高点和最低点均位于图8c,分别约为13 134 N、6 660 N。表明在选定工艺参数范围内,多元工艺参数对主切削力交互影响最显著的是fw-Σ。
4 工艺参数优化
在约束主切削力极值的前提下对车齿工艺参数进行优化时,必须先确定对主切削力影响最大的参数取值,再以最高切削效率为目标,对影响主切削力程度较小的参数进行优化,从而得到一组最佳参数组合。
对切削力影响程度最高的工艺参数是轴向进给量,应先确定其取值再进行优化。但考虑实际加工情况,对刀具螺旋角进行优化(即需要制造新的复杂构型刀具)的经济价值远低于直接调整轴向进给量,并且轴交角对主切削力的影响程度与轴向进给量相差无几,故本文先确定轴交角的取值,再对切削速度与轴向进给量进行参数优化。
为了求取不同螺旋角(本文选取5°、10°、15°,车齿加工时对应的轴交角分别为20°、25°、30°)刀具在对应主切削力约束条件下的最佳工艺参数组合,将采用遗传算法(genetic algorithm,GA)进行优化求解。
车齿切削效率受到切削速度、进给量的影响,且切削效率与二者线性正相关,切削效率计算公式可表示为
在式(11)约束条件下,以式(14)中所示Egs值最大为目标,优化出最佳工艺参数组合。GA算法流程如下。
(1)初始随机产生种群。
(2)依据策略判断个体适应度,若符合优化准则,输出最优个体与最佳解,结束优化;否则进行步骤(3)。
(3)基于适应度选择父母个体,适应度高则被选中概率大,适应度低则被选中概率小。
(4)将成为父母的个体染色体交叉产生后代。
(5)对后代染色体进行变异操作,再进行交叉、变异后产生新的种群,之后回到步骤(2)循环直至产生最优解。
GA 算法的参数范围设置为:l1=(-1~1),l2=(-1~1),l3=(-1、0、1)。车齿工艺参数优化结果如图9 和表5 所示。
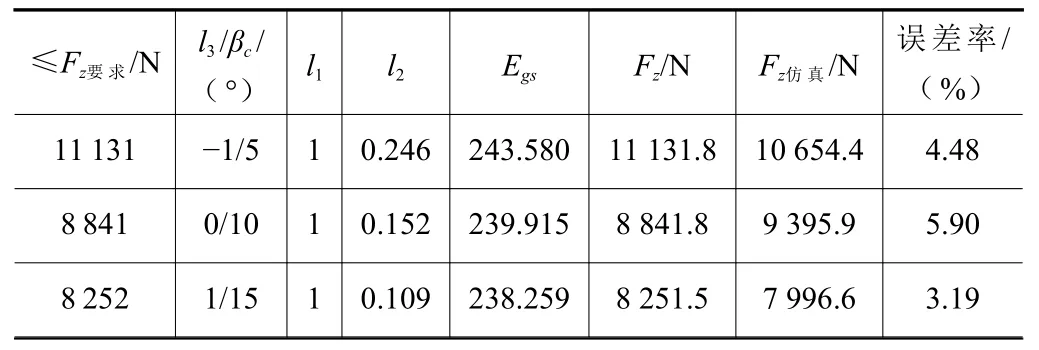
表5 车齿工艺参数优化结果
通过表5 可知,3 组优化参数下所预测主切削力与仿真所得实际主切削力间误差率分别为4.48%、5.90%、3.19%,平均误差率为4.52%,低于10%,表明工艺参数优化具有可靠性、有效性。
5 结语
根据车齿工艺运动学原理,构建了单刀齿与齿槽模型,并利用有限元仿真方法得到不同工况下主切削力变化趋势,得出以下结论:
(1)基于BBD 响应面法建立主切削力预测模型并验证了该模型的正确性,通过分析边际方程图得到了单工艺参数对主切削力的影响规律,即在指定参数范围内,进给量、轴交角、切削速度对主切削力的影响程度依次减弱;之后通过响应曲面图分析多元工艺参数对主切削力的交互影响,结果表明,fw-Σ对主切削力的影响最大。
(2)提出了一种基于GA 算法在约束主切削力前提下以最高切削效率为目标的优化方法,对不同螺旋角刀具进行工艺参数优化,优化结果与实际结果间平均误差率仅为4.52%,可以为实际生产提供指导。
