立足体验式教学，发展数学核心素养

张锡文

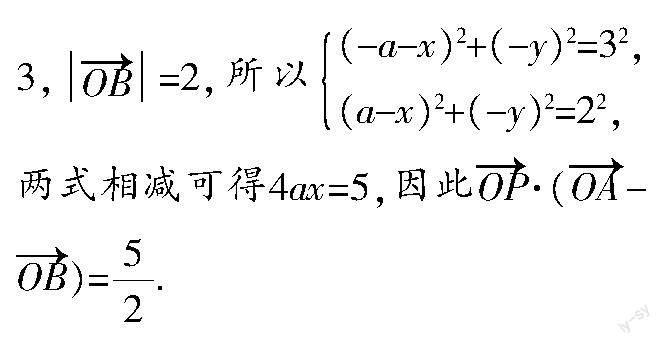
［摘  要］ 体验式教学法能有效提升学生在学习中的获得感，实现深度学习，发展核心素养. 文章从“体验概念形成过程，提升抽象与概括能力”“体验解题思考过程，发展逻辑推理能力”“体验知识建构过程，发展数学建模能力”“体验兴趣激发过程，提升意志品质与人文素养”四方面对如何立足体验式教学，发展数学核心素养展开阐述.

［关键词］ 体验式教学；核心素养；逻辑推理

章建跃认为，真正的数学教学应建立在学生原有认知经验的基础上，引导学生亲历知识的形成与发展过程，形成深刻体验，达成知识的主动建构［1］. 然而，有些教师受传统教学方式的干扰，在教学理念的认识上存在不足，造成课堂体验式教学缺乏真实性与实效性. 因此，本文结合教学实际情况，具体谈谈体验式教学与高中数学教学如何有机融合，以发展学生的各项数学能力，提升学生的数学核心素养.

体验概念形成过程，提升抽象与概括能力

概念、公式、定理等具有高度的抽象性与概括性，是数学教学的基础. 每一个概念或公式的形成与发展，都存在一定的生活背景，教师若将概念或公式直接呈现给学生，让学生机械式地记忆并应用，不仅让学生觉得数学是一门枯燥的学科，还会从一定程度上严重消减学生学习的积极性，这种教学方式不利于学生个体发展.

真正意义上的数学概念、定理、法则或公式等的教学，应将它们的形成与发展过程“重现”在学生面前，让学生通过一定的生活情境亲身体验其抽象过程，从而对它们的内涵与外延形成深刻理解，为学生灵活应用奠定基础. 让学生产生良好体验的最好方式就是创设逼真、丰富的教学情境，让学生在情境体验中切身体会概念、公式等的抽象过程，并从中感知数学学科独有的美.

例1 “圆锥曲线”的教学.

课堂初始，教师可向学生展示类似于图1的图片，让学生从图片中寻找自己感兴趣或熟悉的图形. 通过观察，学生很快就能从图中发现椭圆. 为了增加学生对椭圆的形象认识，教师可带领学生再列举一些生活中与椭圆相关的实例.

随着学生的积极性被调动起来，教师将课前准备好的细绳分发给各个小组，要求各小组成员在教师的指令下，通过合作的方式利用这些细绳画出椭圆. 学生通过合作成功画出椭圆后，再让四名学生（两两合作）到黑板上进行操作演示，由全体师生共同评判哪一组学生画出来的椭圆又快又好.

基于生活实例与动手操作，要求学生对椭圆的定义进行归纳总结. 此过程所耗费的时间并不多，而且学生通过生活实例的列举，会发现椭圆与生活实际有着密切联系. 同时，在合作画图的过程中，不仅锻炼了学生的团结协作能力，还让学生切身体会了椭圆形成的过程，对椭圆的认识从感性层面逐渐上升到理性层面，为接下来的深入教学奠定了基础.

不论是生活实例的列举，还是动手操作画椭圆，都让学生产生了良好的情境体验. 这种情境体验是诱发学习的根本，也是驱动学生产生探索欲的基础. 因此，这是一种影响深远的情境体验，会给学生留下深刻的印象，潜移默化中能提升学生的抽象与概括能力，而抽象与概括能力又是发展学生数学核心素养不可或缺的基石.

体验解题思考过程，发展逻辑推理能力

想让静态的知识转化成动态的能力，学生需要经历一个分析与突破的过程. 解题教学作为数学教学的“重头戏”，需要教师花费大量的时间与精力去研究它的价值. 究竟该如何让学生在解题教学中发展“四基与四能”呢？实践发现，将学生置于具體的问题情境中，让学生体验知识的逻辑性，可有效打破学生原有的认知结构，为建构新知搭建平台.

为了达到这个目的，教师可结合学生的最近发展区与认知特点，创设具有一定挑战性的问题或“形近质异”的问题，让学生体验思考与纠结的过程，经过一番思想斗争获得豁然开朗之感. 这种教学方式，既可让学生感知解题思路的严谨性与周密性，又能悄然提升学生的逻辑推理能力，为核心素养的发展奠定基础.

例2 已知函数f（x）=8x2+16x-k与函数g（x）=2x3+5x2+4x，k是实数，对于任意实数x∈［-3，3］，f（x）≤g（x）都成立，k的取值范围是多少？

因为两个函数的变量是相同的，学生基于原有知识和经验，很快就构造出了一个“差函数”h（x）=g（x）-f（x）=2x3-3x2-12x+k，这样将原问题转化成了“对于任意实数x∈［-3，3］，h（x）≥0都成立，求k的取值范围”，接下来利用导数即可获得k≥45.

学生解答本题的思路清晰，过程合理. 为了训练学生的数学思维，发展学生的逻辑推理能力、转化与化归能力，笔者在此基础上又设计了以下几道变式题（前面条件不变）.

变式题1：如果有实数x∈［-3，3］，能让f（x）≤g（x）成立，则实数k的取值范围是多少？

变式题2：如果对任意实数x，x∈［-3，3］，均有f（x）≤g（x）成立，则实数k的取值范围是多少？

变式题3：如果对任意实数x∈［-3，3］，一直存在实数x∈［-3，3］，能使f（x）=g（x）恒成立，则实数k的取值范围是多少？

变式题4：如果对任意实数x∈［-3，3］，一直存在实数x∈［-3，3］，能使f（x）≥g（x）恒成立，则实数k的取值范围是多少？

上述4道变式题是基于学生最近发展区而设计的，虽然最后均能转化成函数的最值问题或值域问题，但化归过程对学生而言确实是一个挑战，学生的逻辑思维须经历较多的波折才能通过问题的考验.

通过对这组变式题的探究，学生充分体验到了“存在”与“恒成立”的本质与区别，对这一类问题实现了触类旁通. 变式探索使学生的数学思维上升到了一个新的台阶，学生的逻辑推理能力得到了有效发展，同时进一步提升了学生的转化与化归能力. 因此，在解题教学中适当地增加变式训练，是促进学生数学核心素养发展的主要手段之一.

体验知识建构过程，发展数学建模能力

数学建模能力的发展是数学界重点关注的问题，然而调查发现，我国当前中学生的数学建模水平并不理想. 究其主要原因，一方面是因为建模能力的发展对学生的综合能力的要求较高，需要学生拥有较强的识别与提炼数学信息的能力，同时还要有灵活应用数学思想方法解决问题的能力. 另一方面是因为教师自身水平阻碍了学生建模能力的发展［2］.

鉴于此，教师应紧跟时代的步伐，不断积累教学经验并更新教学理念. 同时，要引导学生自主罗列知识框架或网络图，为建模做准备. 在实际教学中，教师以解决具体问题为引领，可让学生通过独立思考与合作学习的方式解决问题，尤其是一题多解的应用，能优化学生的解题思维，完善学生的解题系统，让学生在解题方法的类比中获得融会贯通的能力，从而促进学生建模能力的提升.

解法1适用于填空题或选择题，只要是符合题意的条件都可以用来求解，即选取一种特殊情况，可快速获得结论，这也体现了学生思维的灵活性.

解法2具有一般性，对学生的基本功有一定的要求. 学生只有在熟练掌握向量知识并具备一定的运算能力的基础上，才能顺利完成解题.

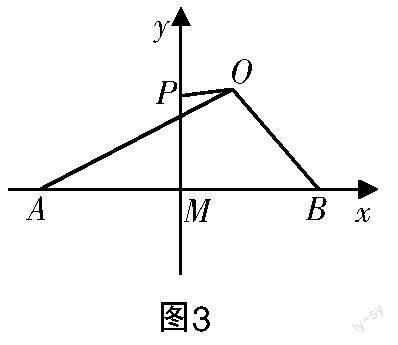
解法3是解决向量问题行之有效的方法之一，它虽然降低了思维要求，但需要学生熟悉直角坐标系的建立过程，以及向量的坐标运算. 此外，教师可以鼓励学生表述其他想法或解法，并与学生一起回顾本章节所涉及的知识体系.

向量是研究数学问题常用的一种工具，在处理问题中具有其他数学方法无可比拟的优势. 在实际教学中，一些学生对这部分知识掌握得不牢固，遇到一些新颖问题时就手足无措，容易产生畏惧感. 因此，在本章节教学中，教师应从一些典型例题出发，带领学生体验一题多解的乐趣，感知知识的系统性与灵活性，让学生形成模型思想，从而促进学生解题能力的提升.

体验兴趣激发过程，提升意志品质与人文素养

俗话说：兴趣是学习最好的老师. 学生一旦对数学产生了浓厚的探究热情，学习就会成为一种自发行为，无需教师过多介入，学生就会自主投入时间与精力进行深入探究. 那么，究竟该如何激发学生的学习兴趣呢？事实证明，加强学生在学习过程中的情感体验，让学生充分感知解题带来的成就感是激发学生学习兴趣的手段之一.

例4 已知△ABC中，点B（-6，0），C（6，0），直线AB与AC斜率的乘积为-，则顶点A的轨迹是什么？

解析 假设点A的坐标是（x，y），根据题设条件可知·=-（x≠±6），经化简可得+=1（x≠ ±6），由此可确定点A的轨迹为椭圆，但不包括与x轴的两个交点.

本题难度不大，对学生来说很普通，解题不会带来太多的体验. 为了有效激发学生的探究欲，笔者在此处顺应学生的思维，鼓励学生以独立思考或合作交流的方式对本题进行改编，以培养学生的创造意识. 学生编拟出来的典型问题如下.

传统教学模式是教师提出问题，学生解决问题，而这里笔者将提问和解题的主动权交给学生，先让学生自主编拟问题并解决问题，然后在学生解题的基础上再进行适当的点拨与引导. 这种教学模式不仅充分体现了学生在课堂中的主体地位，还从真正意义上激活了学生的数学思维，激发了学生的探究热情，让每一个学生都充分体验到了学习乐趣.

此时笔者“趁热打铁”，在问题（2）的基础上要求学生进一步求证：椭圆+=1上，任何关于椭圆中心对称的两点A，B与椭圆上非点A，B的任意点连线斜率的乘积恒为定值-.

学生的思维随着问题的延伸拾级而上，通过对问题的探索与解决，学生不仅感知了数学知识的变化莫测与博大精深，还深刻体验到了数学学习带来的成就感，尤其是不断深入的探索过程，有效培养了学生的意志品质与人文素养.

教育是什么？爱因斯坦和怀特海一致认为：教育就是当学习者将在学校获得的知识都忘掉后所剩下的部分. 这句话完美地诠释了教育的真谛是“通过教育而获得能力”，这种能力可以是学生自主探究的能力、灵敏的判断力与处理问题的能力，也可以是一种精神或智慧［3］. 在教学过程中，鼓励学生自主命题、解题、延伸，就是对学生思维的训练与能力的培养，这种教学方式体现了“以数启智”的教育核心价值，是体验式教学的主要目标.

总之，体验式教学是新课改推进下的一种重要的教学方式，是凸显学生主体性的重要载体. 教师不仅要与时俱进更新自身的教育教学理念，提高自身的认知水平，还要在充分尊重学生的基础上带领学生在“寓教于乐”中突破学习障碍、体验数学魅力，提升学生的数学核心素养.

参考文献：

［1］ 曹才翰，章建跃. 数学教育心理学［M］. 北京：北京师范大学出版社，2006.

［2］ 孙翔宇. 上海市高中生數学建模能力的调查与分析［J］. 教育测量与评价，2016（06）：44-49.

［3］ 张淑梅，何雅涵，保继光. 高中数学核心素养的统计分析［J］. 课程·教材·教法，2017，37（10）：50-55.