利用ARIMA－SSA－LSTM组合模型的碳排放交易价格预测

炊婉冰　吕学斌

摘 要：单一的预测方法在不同方面各有优劣，为了提高碳排放交易价格预测的精确度，从智能算法出发提出ARIMA－SSA－LSTM组合碳排放交易价格预测模型。该模型通过结合非线性规划局部搜索的优势和遗传算法全局搜索的优势使用非线性规划遗传算法分配差分整合移动平均自回归（ARIMA）模型和麻雀搜索算法优化后的长短時记忆（LSTM）模型（SSA－LSTM）的权重，通过加权得到最终的碳排放交易价格预测结果。运用ARIMA－SSA－LSTM组合模型，ARIMA模型，LSTM模型和SSA－LSTM模型分别对湖北省与广东省碳排放交易价格进行短期和长期预测。实证结果表明，相比单一的ARIMA模型、LSTM模型、SSA－LSTM模型，ARIMA－SSA－LSTM组合模型三个预测精度评价指标均为最小，碳排放交易价格预测精度最优。相比于传统ARIMA模型，机器学习LSTM模型具有更精确的预测结果，并且趋势预测更优。引入智能算法后，权重分配结果更加准确，LSTM模型的预测性能得到提升，印证了智能算法在碳排放交易价格预测领域的有效性。

关键词：应用统计；碳排放交易价格预测；加权组合；非线性规划遗传算法；麻雀算法；LSTM模型；ARIMA模型

中图分类号：F 224文献标志码：A 文章编号：1672-9315（2023）05-1025-10

DOI：10.13800/j.cnki.xakjdxxb.2023.0520

Carbon emissions trading price prediction based onARIMA－SSA－LSTM combination model

CUAN Wanbing，L Xuebin

（College of Mathematics and Science，Nanjing Tech University，Nanjing 211816，China）

Abstract：A single prediction method has its advantages and disadvantages in different aspects.In order to improve the accuracy of carbon emissions trading price prediction，an ARIMA－SSA－LSTM combination model is established for carbon emissions trading price prediction.This method uses nonlinear programming genetic algorithms to allocate the weights of Autoregressive Integrated Moving Average（ARIMA）model and the  Long Short－Term Memory（LSTM）model optimized the sparrow search algorithm（SSA－LSTM）.

And the advantages of local search in nonlinear programming are combined with the advantages of global search in genetic algorithms to obtain the final carbon emissions trading price prediction result through weighting.Using the ARIMA－SSA－LSTM combination model，ARIMA model，LSTM model and SSA－LSTM model，the short－term and long－term carbon emissions trading price in Hubei Province and Guangdong Province are predicted respectively.The empirical results show that，the ARIMA－SSA－LSTM combination model has the smallest prediction accuracy evaluation indicators and the best prediction accuracy of carbon emissions trading prices over the single ARIMA model，LSTM model and SSA－LSTM model.Compared to traditional ARIMA models，the machine learning LSTM models have more accurate prediction results and better prediction trends.In addition，by the introduction of intelligent algorithms in this article，the weight allocation results are more accurate，and the prediction performance of the LSTM model is improved，confirming the effectiveness of intelligent algorithms in the field of carbon emissions trading price prediction.

Key words：applied statistics；carbon emissions trading price prediction；weighted combination；nonlinear programming genetic algorithm；sparrow search algorithm;LSTM model;ARIMA model

0 引 言

随着世界经济的快速增长，温室气体排放量急剧增加，对气候和环境构成了前所未有的威胁。为维护世界经济社会的可持续发展，世界上各经济体逐步推行设立国际碳排放权交易的计划。每年有大量的碳排放商品在市场上交易，在碳交易市场中，碳排放交易价格可以说是最重要的部分，价格的波动影响这个市场的变化。因此对碳排放交易价格的合理分析与预测能更好地指导碳市场参与者的行为与决策，推动碳金融市场的理性发展[1]。

关于碳排放交易价格预测，国内外许多学者已经提出了许多预测模型，包括统计模型、机器学习模型、组合模型等。吴孟操利用ARIMA模型对上海市试点碳交易价格进行建模预测分析，得出ARIMA模型能够很好地模拟上海市碳交易权价格趋势[2]；ZHAO等研究发现以欧洲斯托克50指数为解释变量构造的回归模型可以明显提高碳排放交易价格的预测精度[3]；高仲芳提出利用GARCH族模型进行碳排放交易价格波动的预测，并比较多种GARCH模型，针对不同碳市场选择最合适有效的GARCH预测模型[4]；CHEVALLIER采用非参数模型对欧洲环境交易所碳现货价格和欧洲气候交易所碳期货价格进行了预测[5]，发现非参数模型的预测精度高于自回归模型；刘家钰选择支持向量机和随机森林两种模型进行碳排放交易价格建模、預测并从宏观和微观的角度提出相关建议[6]；郭蜀航建立BP神经网络模型对碳排放交易价格进行定量研究，并与传统多元模型进行比较，验证了BP神经网络模型在碳排放交易价格预测更好的预测效果[7]。除了上述模型，统计模型还有多元回归模型[8]、随机波动模型[9]等；机器学习模型还有灰色预测模型[10]、多层感知器神经网络模型[11]等。碳排放交易价格数据是不稳定的非线性数据，传统的统计模型在平稳序列中具有预测优势，不能有效地解决非线性数据。机器学习模型对非线性数据有较好的适应性，但可理解性较差。为了打破单一模型的局限性，整合不同模型的优势[12]，部分学者开始考虑组合模型进行预测。大部分组合模型以“分解-预测-集成”的思想为主，姚奕等利用经验模态分解（EMD）将湖北碳排放交易价格分解并重构为高频分量、低频分量和趋势分量，结合支持向量机对各分量进行预测，提高了预测精度[13]；全从新采用变分模态分解方法（VMD）将欧盟碳排放配额现货价格分解为不同频率的模态分量，使用极限学习机对各分量进行预测，相比与EMD分解，预测精度得到提高[14]。也有学者从最优权重角度构建组合模型，谢旭升等从最优权重角度建立了ARMA－BP加权组合碳排放交易价格预测模型，并将其与单一模型的预测结果进行比较[15]，发现ARMA－BP最优权重组合模型具有更高的预测精度。近些年来智能优化算法发展迅速，在很多领域都得到了应用。部分研究学者借鉴智能算法在其他领域的应用，将智能算法引入碳排放交易价格预测领域，进一步提高了组合模型的预测效果。赵鑫等提出利用鲸鱼优化算法优化LSTM模型再将其引入组合预测模型，可以有效地提高碳排放交易价格的预测准确率[16]；江丹丹提出利用多目标灰狼优化算法（IMOGWO）优化极限学习机（ELM），然后将其引入分解集成模型来预测碳排放交易价格，不仅预测精度高，而且具有较好的稳定性[17]。

基于上述研究现状发现目前对碳排放交易价格预测的研究并不成熟，因此从多角度、多方法进行分析碳排放交易价格仍然是众多学者追求的目标。选择传统统计学方法中的 ARIMA模型和机器学习方法中的LSTM模型建立加权组合模型进行预测。为了提高LSTM模型的预测精度，使用麻雀搜索算法对LSTM模型中的超参数进行参数寻优。通过引入非线性规划遗传算法分配单一模型权重，获得最优权重，这种权重分配方式融合了非线性规划分配权重时有较强的局部搜索能力的优点和遗传算法分配权重时有很好的全局搜索能力的优点[18]，最后加权得到更精确的碳排放交易价格组合预测值。中国目前存在七个碳交易试点基地，选取交易频繁、数据量充足的湖北省和广东省碳交易市场碳排放交易价格数据做实证分析。

1 单一模型

1.2 LSTM模型

长短时记忆（LSTM）是一种特殊的RNN模型。与传统的神经网络相比，它可以解决长期依赖、梯度消失和梯度爆炸等问题[20]。此外，LSTM模型在固定分量较多的不稳定时间序列中表现更好[21]。模型流程如图1所示。

长短期记忆网络（LSTM）运行主要依靠3种门控单元来维持数据的更新和控制。这3种门控单元主要包含遗忘门、输入门、输出门。

1.3 SSA－LSTM模型

为了提高LSTM模型的预测准确率，尝试使用麻雀搜索算法对LSTM中的进行超参数寻优，构建SSA－LSTM模型。

麻雀搜索算法（Sparrow Search Algorithm，SSA）是薛建凯等在2019年提出一种模拟生物系统中群体生活习惯的群体智能优化算法，此算法通过模拟麻雀的觅食和反捕食过程，将个体分为发现者、跟随者和警戒者，一个个体位置对应一个解，三者位置不断更新，以获得最优解[22]。与传统智能优化算法相比，麻雀搜索算法具有结构简单、容易实现、控制参数不多、局部搜索能力强的优点。该算法在单峰、多峰等基准函数上的表现优于粒子群算法、蚁群算法等传统算法[23]。

基于麻雀搜索算法强大的搜索能力和易于操作的优点，在LSTM模型进行预测之前先利用麻雀算法搜索LSTM模型的最优超参数，使得LSTM模型的预测效果得到提升，进而得到更优的预测值。通过麻雀搜索算法优化的LSTM模型超参数为 LSTM网路包含的隐藏单元数目、最大训练周期、分块尺寸、初始学习率、L2参数。搜索过程中，训练LSTM模型时，适应度函数为LSTM对训练集和测试集的预测错误率，其错误率越低越好。其本质为LSTM模型训练后的均方误差（MSE），均方误差越小，表明预测的数据与原始数据重合度越高。

2.1 组合模型构建

考虑到单一算法预测的结果可能在真实值附近波动较大的情况，文中提出运用非线性规划遗传算法分配ARIMA模型和SSA－LSTM模型权重的组合模型来进行碳排放交易价格预测。

假定关于同一碳排放交易价格预测问题，有k（k≥2）种预测方法，记第t期实际观测值为yt，第t期第i种方法的预测值为

是一个典型的非线性规划问题。经典的非线性规划算法大多数采用梯度下降法求解，虽然该方法局部搜索能力强，但全局搜索能力不足，容易陷入局部极值点，难以求得全局最优解。

目前，以遗传算法为代表的一类全局优化能力强的方法在求解复杂优化问题上表现出巨大潜力，遗传算法更适用于处理传统搜索算法难以解决的非线性优化的问题。遗传算法的优点是进行优化前先将问题参数编码成染色体，从而不针对参数自身，不受函数约束条件的限制。遗传算法在优化计算时不依赖于梯度信息，不要求目标函数连续且可导，使其适于求解传统搜索方法难以解决的大规模、非线性组合优化问题。即使如此遗传算法依然存在着容易过早收敛和局部搜索能力差的问题。这些问题在求解非线性、非凸的有约束非线性规划问题时会更加突出。

因此，文中在这里使用非线性规划遗传算法来求解式（11）的优化问题，一方面遗传算法用于全局搜索，另一方面非线性规划算法用于局部搜索，以获得优化问题的全局最优解[25]。在使用非线性规划遗传算法时，个体对应式（11）的解，根据求解问题式（11）初始化种群模块，产生满足一定条件的个体的种群，根据适应度计算选取的最佳染色体。采用轮盘赌法从种群中选择适应度好的个体组成新种群，然后采用单点交叉算子对个体的染色体进行重组，对个体进行变异。每进行一次适应度计算、选择、交叉、变异等于完成一次进化。当进化次数为固定值N的倍数时，将当前所有进化的个体结果作为非线性规划的起始点进行优化，求得进一步的优解。其中非线性规划寻优利用当前染色体值采用Fmincon函数寻找问题的局部最优值[26]。

非线性规划遗传算法的终止条件为平均解与最优解重合。进行终止条件判断前，计算当前所有个体的适应度并记录最优个体适应度，适应度最优的个体为最优解，所有个体的平均值为平均解，当平均解与最优解重合时说明当前种群中大多均为最优解，在一定程度代表当前种群已经较为稳定。满足终止条件的最优解即为所求。非线性规划遗传算法求解问题过程如图2所示。

当序列趋势明显时，统计方法往往能得到更准确的结果，而机器学习方法在具有更多固定成分的不稳定时间序列中表现更好。

文中结合ARIMA模型和SSA－LSTM模型构建ARIMA－SSA－ LSTM权重分配组合模型。ARIMA－SSA－LSTM组合模型流程如图3所示。

2.2 模型评价指标

采用3种常见的预测精度评价指标：均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）来评价预测模型的预测精度。同时采用趋势性指标平均方向精度（MDA）来评价模型的趋势预测效果。当均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）值越小，模型效果越好；当趋势性指标平均方向精度（MDA）值越大，模型的趋势预测效果越好。这些指标定义如下

3 实证分析

3.1 数据选取与处理

选取湖北省碳交易市场和广东省碳交易市场2021年3月1日至2022年3月31日碳排放权交易收盘价格（单位：元/吨）进行实证分析，数据均来自于国泰安数据库。由于碳排放交易价格通常波动较大，或者当天碳市场没有交易，因此原始数据中往往存在异常值和缺失值。对于原始数据中的缺失值和异常值，使用前一天的价格值或前后两天的平均值替换缺失值和异常值，填补后的数据趋势如图4和图5所示。

从图4可以看出，湖北省碳排放交易价格有明显的波动趋势，对其进行平稳性检验，发现其不平稳，对数据进行一阶差分，以获得平稳序列，然后对原始序列进行白噪声检验发现该序列不是纯随机序列，可以建立模型。同理根据趋势图5，以及广东省碳排放交易价格数据的平稳性检验和白噪声检验，可以得到广东省碳排放交易价格数据也不是纯随机序列，可以建立模型。

3.2 短期预测

利用湖北省碳市场和广东省碳市场2021年3月1日至2022年2月28日对2022年3月1日至2022年3月10日的碳排放交易价格进行短期预测。

先对湖北省试点的数据进行分析，首先进行单一模型的预测。针对不同碳市场数据，ARIMA模型得到数据拟合结果不一样，利用湖北省试点数据拟合得到ARIMA（2，1，3）模型，即差分阶数为1阶，自回归阶数为2阶，移动平均阶数为3阶的ARIMA模型，具体形式如下

然后利用ARIMA（2，1，3）模型进行十天预测，得到湖北省碳排放交易价格的十天预测值。

当使用麻雀搜索算法对LSTM模型优化时，针对不同碳市场数据，得到优化结果不一样。其中，设置麻雀搜索算法预警值为0.6，发现者比例为0.7，种群数量为10，最大迭代次數为10。对于湖北省碳市场的数据，通过麻雀搜索算法优化LSTM得到的超参数值见表1，并与原始超参数做比较。根据初始的超参数表与优化过后的超参数表，分别得到LSTM模型的预测值与SSA－LSTM模型的预测值。

基于单一模型预测结果，进一步求解组合模型。首先根据ARIMA模型预测值和SSA－LSTM模型预测值求得权重分配模型所需的预测误差信息矩阵，然后通过非线性规划遗传算法来分配ARIMA模型和SSA－LSTM模型的权重。其中，遗传算法将进化代数设置为30，种群规模设置为100，交叉概率设置为0.6，变异概率设置为0.01。最终ARIMA模型权重为0.038 4，SSA－LSTM模型权重为0.961 6。依据权重分配的结果，计算加权后的组合模型预测值。

将ARIMA－SSA－LSTM组合模型的预测效果与单一ARIMA模型，LSTM模型，SSA－LSTM模型进行对比。预测效果评价指标见表2。预测对比如图6所示。

同理，对广东省碳市场2021年3月1日至2022年2月28日的碳排放交易价格数据进行短期预测，得到ARIMA模型预测值，LSTM模型预测值，SSA－LSTM模型预测值。其中ARIMA模型为ARIMA（0，1，0）模型，具体形式如式（17），SSA算法优化LSTM后得到的超参数值见表3。

同样运用非线性规划遗传算法对广东碳市场单一模型预测值进行权重分配，发现ARIMA模型权重占比 0，SSA－LSTM模型权重占比1。ARIMA－SSA－LSTM组合模型与单一模型的预测效果评价指标见表4。预测对比如图7所示。

由表2可知，对于湖北省碳市场，使用ARIMA－SSA－LSTM组合模型预测碳排放交易价格时，评价指标RMSE、MAE和MAPE最小，表明该模型的预测精度优于其他单一模型方法。对于单一模型，机器学习中的LSTM模型预测效果明显优于统计学ARIMA模型，并且在智能算法优化过后预测效果更加优异。但是进行权重分配时统计学模型的权重并不为0，说明统计学模型并不是完全无用。依然可以对SSA－LSTM模型得到的预测结果进行修正。对于短期预测，趋势预测的差距似乎并不明显。广东省碳市场，使用非线性规划遗传算法分配权重时，ARIMA模型权重占比0，SSA－LSTM模型权重占比1。并不能说明模型失效，说明此时两种单一模型最好的权重分配结果就是ARIMA模型权重占比 0，SSA－LSTM模型权重占比1。ARIMA－SSA－LSTM组合模型评价指标RMSE、MAE和MAPE与SSA－LSTM模型一样为最小，预测精度优于LSTM模型和ARIMA模型。从图6与图7可以看出ARIMA－SSA－LSTM组合预测值与真实值更加贴近。

3.3 长期预测

进一步地，改变预测长度，用湖北省碳市场和广东省碳市场2021年3月1日至2022年2月28日的碳排放交易价格数据预测2022年3月1日至2022年3月31日一个月的碳排放交易价格。湖北省碳市场最终ARIMA模型权重占比

0.006 3，SSA－LSTM模型权重占比0.993 7。广东省碳市场最终ARIMA模型权重占比

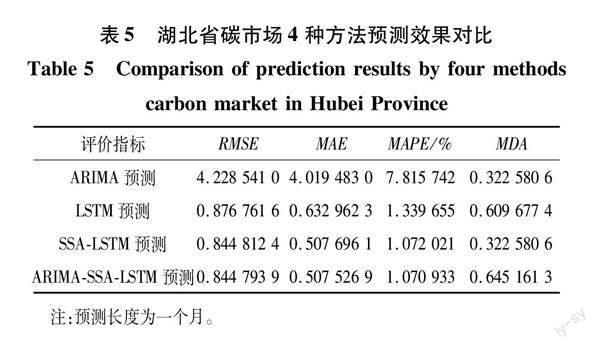
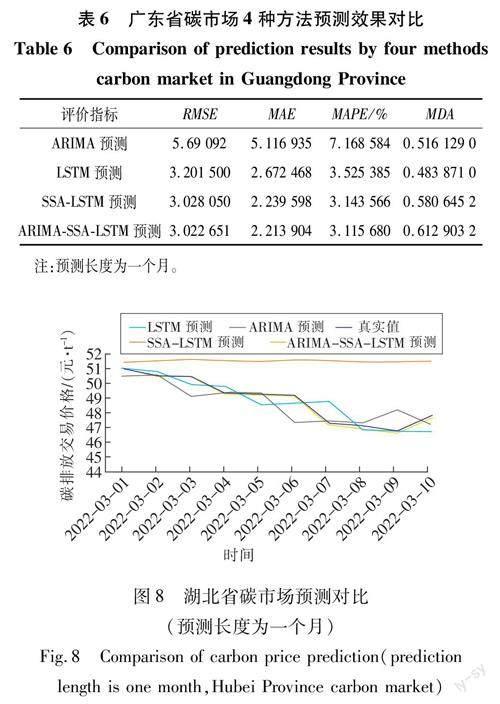
0.036 1，SSA－LSTM模型权重占比0.963 9。分配权重后加权计算组合模型的预测值，ARIMA－SSA－LSTM组合模型和三种单一模型一个月的预测效果评价指标见表5和表6。预测对比如图8和图9所示。

由表5可知，在新的预测长度下，当ARIMA－SSA－LSTM组合模型预测湖北碳排放交易价格时，评价指标RMSE、MAE和MAPE依然最小，表明ARIMA－SSA－LSTM组合模型的预测效果仍然优于其他单一模型。同理对于表6，使用ARIMA－SSA－LSTM组合模型预测廣东省碳排放交易价格时，评价指标RMSE、MAE和MAPE也是最小，更可以表明ARIMA－SSA－LSTM组合模型预测效果优于单一模型。在新的预测长度下的3种单一模型，机器学习LSTM模型依然明显优于统计学ARIMA模型，仍然在进行权重分配时统计学模型的权重并不为0，同样也说明统计学模型并不完全无用，可以对机器学习模型得到的预测结果进行修正。根据趋势性指标MDA的值，发现LSTM模型的趋势预测要明显优于统计学模型。MDA值也验证了机器学习模型在不平稳数据上的表现要比统计学模型要优异，能够更好地预测趋势变动。组合模型在长期预测下，趋势预测也有明显优势。根据图8与图9发现ARIMA－SSA－LSTM组合预测值与真实值更加接近，机器学习模型明显比统计学模型更好的预测出数据的波动。

3.4 总结

综合对比表2、表4～6与图6～9，ARIMA－SSA－LSTM组合模型的预测效果在2个预测长度下预测精度均得到最优的预测结果。对比所采取的3种单一模型，机器学习模型LSTM模型明显优于统计学ARIMA模型，说明机器学习模型充分处理了碳排放交易数据的不平稳性。通过智能算法优化过后的机器学习模型预测精度得到了进一步提升。在长期预测下，根据MDA指标可以明显看出机器学习LSTM模型能够更好的预测数据的变动趋势。对比选取的2个预测长度，可以明显发现所选取的3种单一模型和ARIMA－SSA－LSTM组合模型短期预测精度都优于长期预测精度。基于所得到的结果，可以认定构建的ARIMA－SSA－LSTM组合模型能够得到更准确的碳排放交易价格预测值。

4 结 论

1）使用非线性规划遗传算法分配ARIMA模型和SSA－LSTM模型的权重来构造ARIMA－SSA－LSTM组合模型进行碳排放交易价格预测，此方法的主要步骤是：①通过单一模型预测得到预测值并构建权重分配模型；②使用非线性规划遗传算法分配权重；③根据非线性规划遗传算法权重分配结果进行组合得到最终的预测值。

2）通过对湖北省和广东省碳排放交易价格数据的实证分析发现ARIMA－SSA－LSTM组合模型对碳排放交易价格预测的精度有明显的提高，预测结果更加靠近真实值。并且在选取的碳排放交易数据下，机器学习LSTM模型的预测效果明显优于传统的统计学ARIMA模型。同时在通过智能算法的寻优后LSTM模型得到了最优超参数，模型预测效果得到提升。

3）所构建的模型在湖北省和广东省碳市场的应用，提高了预测精度，在不同碳市场的数据下，模型可以根据数据情况得到不同参数、不同权重，说明模型可以灵活运用于不同的碳市场，因此可以将其拓展到其他碳试点，提高其他碳试点的预测结果。

4）在单一模型优化与模型权重分配中都引入智能优化算法，证实了智能优化算法在碳排放交易价格预测领域的应用的有效性，在未来的研究中可以多加注重智能算法在碳金融领域的应用。

5）模型雖在碳排放权交易价格预测已经有很高的精度，依然存在着改进空间，遗传算法和麻雀算法的部分参数是根据经验设定的，是否可以运用某种法找到这些参数的最优值值得进一步思考。

参考文献（References）：

[1] 张鹏.中国碳排放权交易市场价格影响因素及预测研究[D].北京：北方工业大学，2021.

ZHANG Peng.Analysis of the influencing factors and forecast of carbon emissions trading price in China[D].Beijing：North China University of Technology，2021.

[2]吴孟操.基于ARIMA模型的上海市碳排放权价格分析[J].经济研究导刊，2022（26）：29-31.

WU Mengcao.Price analysis of Shanghai carbon emission rights based on ARIMA model[J].Economic Research Guide，2022（26）：29-31.

[3]ZHAO L T，MIAO J，QU S，et al.A multi－factor integra－ted model for carbon price forecasting：Market interaction promoting carbon emission reduction[J].Science of the Total Environment，2021，796：149110.

[4]高仲芳.碳排放权交易价格：波动特征、影响因素及预测分析[D].曲阜：曲阜师范大学，2021.

GAO Zhongfang.Carbon emission trading price：Fluctuation characteristics，influencing factors and prediction analysis[D].Qufu：Qufu Normal University，2021.

[5]CHEVALLIER J.Nonparametric modeling of carbon p－rices[J].Energy Economics，2011，33（6）：1267-1282.

[6]刘家钰.基于机器学习的国际碳期货价格预测研究[D].天津：天津工业大学，2020.

LIU Jiayu.Research on international carbon futures price forecasting based on machine learning[D].Tianjin：Tiangong University，2020.

[7]郭蜀航.基于BP神经网络的碳排放权交易价格预测——以湖北省为例[D].武汉：中南财经政法大学，2020.

GUO Shuhang.Prediction of carbon emission trading price based on BP neural network：Taking Hubei Pro－vince as an example[D].Wuhan：Zhongnan University of Economics and Law，2020.

[8]FAN X，LI S，TIAN L.Chaotic characteristic identification for carbon price and a multi－layer perceptron network prediction model[J].Expert Systems with Applications，2015，42（8）：3945-3952.

[9]HARALDSSON H ，GUEBRANDSDTTIR H N.Predicting the price of EU ETS carbon credits[J].Systems Engineering Procedia，2011（1）：481-489.

[10]LYU J，CAO M，WU K，et al.Price volatility in the carbon market in China[J].Journal of Cleaner Production，2020，255：120171.

[11]牛丽文，李丽娜.基于GM（1，1）模型的市场碳交易价格预测——以北京、广东、湖北为例[J].中小企业管理与科技，2021（5）：106-108.

NIU Liwen，LI Lina.Prediction of market carbon trading price based on GM（1，1）model：Taking Beijing，Guangdong and Hubei as examples[J].Management & Technology of SME，2021（5）：106-108.

[12]BATES J M，GRANGER C W J.The combination of forecasts[J].Journal of the Operational Research Society，1969，20（4）：451-468.

[13]姚奕，吕静，章成果.湖北碳市场价格形成机制及价格预测[J].统计与决策，2017（19）：166-169.

YAO Yi，LYU Jing，ZHANG Chengguo.The price formation mechanism and price forecast of carbon market in Hubei Province[J].Statistics ＆ Decision，2017（19）：166-169．

[14]全从新.基于ELM－VMD混合模型的碳价预测研究[D].北京：华北电力大学，2018.

QUAN Congxin.Carbon price forecasting based on combination of VMD and ELM[D].Beijing：North China Electric Power University，2018.

[15]谢旭升，严思屏.基于ARMA－BP组合模型的碳排放交易价格预测——以福建省为例[J].龙岩学院学报，2021，39（2）：107-115.

XIE Xusheng，YAN Siping.Carbon emission trading price prediction based on ARMA－BP combination model：A case study of Fujian Province[J].Journal of Longyan University，2021，39（2）：107-115.

[16]赵鑫，陈臣鹏，毕贵红.基于多模式分解的碳交易价格组合预测模型[J].电力科学与工程，2022（38）：52-58.

ZHAO Xin，CHEN Chenpeng，BI Guihong.Combination prediction model of carbon trading price based on multi－mode decomposition[J].Electric Power Science and Engineering，2022（38）：52-58.

[17]江丹丹.基于改进的多目标灰狼优化算法的碳交易价格预测[D].兰州：兰州大学，2020.

JIANG Dandan.Carbon trading price prediction based on improved multi－objective grey wolf optimization algotithm[D].Lanzhou：Lanzhou University，2020.

[18]韦凌云，柴跃廷，赵玫.不等式约束的非线性规划混合遗传算法[J].计算机工程与应用，2006，42（22）：46-49，65.

WEI Lingyun，CAI Yueting，ZHAO Mei.A hybrid gene－tic algorithm for solving nonlinear programming problems with inequality constraints[J].Computer Engineering and Applications，2006，42（22）：46-49，65.

[19]王燕.应用时间序列分析[M].北京：中国人民大学出版社，2015.

[20]HOCHREITER S，SCHMIDHUBER J.Long short－term memory[J].Neural Computation，1997，9（8）：1735-1780.

[21]翟梦梦，王旭春，任浩.基于Python的LSTM模型对流感预测的研究[J].中国卫生统计，2022，39（2）：162-166，171.

ZHAI Mengmeng，WANG Xuchun，REN Hao.Study on LSTM model based on Python in prediction of influenza[J].Chinese Journal of Health Statistics，2022，39（2）：162-166，171.

[22]薛建凱.一种新型的群智能优化技术的研究与应用——麻雀搜索算法[D].上海：东华大学，2019.

XUE Jiankai.Research and application of a novel swarm intelligence optimization technique：Sparrow search algorithm[D].Shanghai：Donghua University，2019.

[23]李雅丽，王淑琴，陈倩茹.若干新型群智能优化算法的对比研究[J].计算机工程与应用，2020，56（22）：1-12.

LI Yali，WANG Shuqin，CHEN Qianru.Comparative study of several new swarm intelligence optimization algorithms[J].Computer Engineering and Applications，202

0，56（22）：1-12.

[24]王圃，陈荣艳，孙晓楠.加权组合模型在城市用水量预测中的应用[J].应用基础与工程科学学报，2010，18（3）：428-434.

WANG Pu，CHEN Rongyan，SUN Xiaonan.Application of weighted combination model in urban water consumption prediction[J].Journal of Basic Science and Engineering，2010，18（3）：428-434.

[25]厉美璇，闫春，靳旭玲.基于组合预测的变压器故障诊断模型[J].数学建模及其应用，2020，9（4）：49-56.

LI Meixuan，YAN Chun，JIN Xuling.Transformer fault diagnosis model based on combinatorial prediction[J].Mathematical Modeling and Its Applications，2020，9（4）：49-56.

[26]史峰，王辉，郁磊.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011.

（责任编辑：高佳）

收稿日期：2023-03-15

基金项目：国家自然科学基金项目（12071071）

第一作者：炊婉冰，女，河南洛阳人，硕士研究生，E－mail：1205428937@qq.com

通信作者：吕学斌，女，河南南阳人，博士，副教授，E－mail：lvxuebin2008@163.com