铁路车辆悬挂件振动疲劳评估与结构优化研究
2023-11-10杨勇军李国顺张晓峰朱小波
杨勇军,李国顺,张晓峰,朱小波
(1 中车戚墅堰机车有限公司,江苏常州 213011;2 中国铁道科学研究院集团有限公司 机车车辆研究所,北京 100081)
近年来有多款新型铁路车辆在投用后短期内发生了一些辅助设施的悬挂安装结构件(如天线梁、沙管支架、防碰撞支架等)因结构疲劳强度不足引起的开裂故障,危及行车安全。对相关故障进行深入研究,发现其中大多数故障有显著的共同特点,即故障多发部位的动应力(或其他振动参数)与车辆运行速度关系密切,常在某速度区间出现大幅振荡现象。此类疲劳问题可归为振动疲劳,同类问题也广泛出现于航空航天、能源动力设备等多个工程领域。
近半个世纪以来,随着人们研究的深入,对振动疲劳的认识及相关理论在持续发展中。Crandall于1963 年将振动疲劳定义为交变载荷产生的具有损伤累积特征的破坏现象[1];姚起杭等经长期对飞机结构疲劳问题的研究,从共振角度给出了振动疲劳的定义[2]。孟凡涛等采用ANSYS 软件对飞机机翼进行了频域应力响应功率谱分析,并利用三区间法对结构寿命进行了预测[3];花新华等利用Dirlik 法和Miner 准则对车下设备安装座在标准载荷功率谱密度作用下的疲劳损伤进行了仿真评估[4];曹明红等分析了不同幅值概率密度模型的计算精度,研究认为当前多数宽带频域疲劳寿命估算方法不计应力循环均值是合理的[5-6]。针对焊接结构疲劳问题,董平沙等研究认为焊接残余应力对疲劳寿命的影响很小,虽然残余压应力能延长疲劳寿命,但要利用这一点是很难实现的[7-8]。
针对铁路车辆结构件的振动疲劳问题,如何开展错频设计或频率错开多少才能有效避免振动疲劳的发生,目前为止尚没有指导性建议。文中在既有研究成果的基础上,对相关理论、疲劳强度评估和疲劳性能提升方法进行梳理和应用研究,分析研究了频率比对振幅的影响;通过实例系统地展示了激励来源分析及结构优化的全过程,可为相关工程应用提供借鉴。
1 基本理论研究
1.1 频率比和结构阻尼对振幅的影响
对于固有频率已确定的系统,其振动振幅除了载荷大小和系统刚度外,主要受载荷频率与固有频率之比λ和系统阻尼大小的影响。金属或非金属材料自身的结构阻尼可用无量纲损失因子η来表示,对于金属、木材及混凝土,损失因子范围为0.001~0.01[9]。
考虑一个损失因子为η的单自由度系统,在简谐激励P0sinωt下稳态响应的振幅放大因子β,表示系统的位移振幅相对于静载荷P0下静态位移的放大系数,其受频率比λ和损失因子η的影响为式(1)[9]:
式 中:β为 振 幅 放 大 因 子;λ为 频 率 比;η为 损 失因子。
1.2 疲劳累积损伤理论
针对金属材料的疲劳损伤(或扩展)程度问题,研究人员提出了多种理论进行量化。这些理论按照多次载荷循环的损伤累加方式可分为线性累积和非线性累积2 大类。其中,线性疲劳损伤累积理论的典型代表是Palmgren-Miner 准则(以下简称Miner 准则),为式(2):
式 中:D为 总 损 伤;ni为 第i级 应 力 的 循 环 数;Ni为疲劳性能S-N曲线第i级应力对应的疲劳寿命。
1.3 Miner 准则应用于焊接结构的特殊性
车辆上焊接结构各部位应力的分布是十分复杂的,体现在行驶过程中随时间历程的随机性和在焊缝各方向分布的复杂性。针对后者,公开发表的文献提出了3 个表征结构节点应力的概念即名义应力、热点应力和结构应力[10],以及通过测试和理论计算获取这3 类应力的方法。相应地,表示焊接接头疲劳性能的S-N曲线也应根据应力类型分别获得并匹配使用。国际焊接学会2008 年发布 的IIW-1823-07 号 文 件[11]和 英 国2015 年 发 布 的BS 7608-2015 标准[12],列出了若干基于名义应力法和热点应力法的常见钢制焊接接头S-N曲线。其中,适用于变幅载荷的S-N曲线形式如图1 所示,其横坐标为循环数即疲劳寿命N,纵坐标为应力循环范围Δσ,表征拐点两侧曲线斜率的参数m1为3、m2为5。

图1 焊接接头典型S-N 曲线(双对数坐标)
2 车辆悬挂件振动疲劳强度评估方法研究
2.1 基于随机载荷谱的仿真评估
鉴于轨道激励载荷的随机性,虽然通过实际车辆的线路试验可获得悬挂件所经受载荷大量的实测时域信号,但由于计算量庞大,难以利用有限元法直接进行基于载荷时域信号的结构瞬态响应应力的仿真及评估。取而代之的是在频域内进行仿真评估,首先获得载荷的频域统计数据(以下以功率谱密度为例),将它作为结构动力响应分析的输入,仿真得到结构响应应力的功率谱密度,为式(3):式中:G(f)为响应应力的功率谱密度;W(f)为激励载荷的功率谱密度;H(f)为响应应力与激励载荷之间的传递函数;|H(f)|为其幅频特性,可由有限元模型作频率响应分析得到。
在此基础上,根据Dirlik 方法[4-5]或利用文献[13]的公式可计算得到应力幅值概率密度;最后依据S-N曲线和Miner 准则(式(4))计算得到载荷谱作用时间T内的疲劳损伤D,D大于失效临界值DCR即认为存在失效风险。
式中:D为总损伤;EP为响应应力的峰值期望值,M4、M2分别为应力功率谱密度G(f) 的4 阶矩和2 阶矩,其值可按式(5)计算;T为载荷作用时间;p(S)为响应应力的幅值概率密度;C、m分 别 为S-N曲 线 方 程(N⋅Sm=C)的常数,若S-N曲线有拐点如图1 所示,那么拐点两侧C、m的 值 不 同;DCR为 失 效 临 界 值,等 于T与 悬 挂件寿命要求的总时间之比。
式中:G(f)为应力功率谱密度;f为频率;Mr为应力功率谱密度的r阶矩。
2.2 台架试验
为评估装于铁路车辆的设备承受铁路特有随机振动和冲击的能力,国际电工委员会收集了世界各地有关机构根据标准调查程序获得的车辆典型部位(车轴安装、转向架安装和车体安装)的振动加速度数据,经统计分析和推演,以IEC 61373标准[14]形式发布了不同部位所装设备基于宽带随机振动的试验载荷谱和试验程序。车辆悬挂件可按该标准在实验室进行模拟长寿命的振动试验,用于确定试验频率范围内的振动疲劳强度薄弱部位。
2.3 线路试验
实车线路动强度试验对识别出的关键和危险部位进行动应力测试,可用于评估被测结构的疲劳性能。测得的应力数据经循环计数和分级统计,再根据测点部位的S-N曲线,按照Miner 准则和损伤等效原则由式(6)计算得到等效到标称循环数(200 万次)的应力(简称等效应力):
式中:△σeq,2E6为等效到标称循环数(200 万次)的应力;D0为允许损伤,对于在典型条件下完成的动应力测试,允许损伤可简单取为动应力数据所代表的测试里程与悬挂件寿命要求的总里程之比,否则应考虑附加不确定系数;△σi为第i级应力;ni为第i级应力的循环数;m1为S-N曲线拐点上方曲线负 斜 率 的 倒 数;当△σi<△σK时m=m1+2、b=△σ-2K,否 则m=m1、b=1,其 中△σK为S-N曲 线 拐点对应的应力,如图1 所示。
若等效应力小于相应的疲劳许用应力,则评估通过,反之评估不通过[15]。车辆维护保养状态、列车操纵条件、线路和环境条件等对测试数据会有影响,故计算允许损伤时应根据经验附加一个不确定系数。
3 疲劳失效原因分析及抗疲劳设计和控制举措
对于车辆悬挂件疲劳失效原因的调查,可通过实车运行时关键部位动应力和加速度的测试分析了解载荷频率分布和动应力水平、以及结构有限元仿真分析了解结构模态和理论应力水平,两者相结合,基本能够判断失效是否与特定的激励源密切相关[16],或者仅仅由于结构设计不合理而引起的疲劳失效。若激励频率与系统固有频率接近且在固有频率附近有较高的振动能量,则属于振动疲劳;反之属于静态疲劳。
对于振动疲劳,可从控制振源和优化结构2 方面降低结构动应力、延长使用寿命。控制振源方面,根据主要激励能量来源可考虑:
(1)通过旋轮、打磨钢轨等措施改善轮轨运行条件。
(2)采取限制旋转设备转速、限制车辆运行速度等方式控制激励的频率范围。
(3)通过优化运行策略减少共振频带附近的工作时间。
(4)采取隔振、附加阻尼等措施衰减振动能量。
结构优化方面,主要是进行结构动力学设计,使结构固有频率避开车辆运行中的常见激励频率,从而降低结构响应应力。当然,通过优化结构的构造形式以降低应力集中和优化工艺以消除制造缺陷,以及优化残余应力等适用于抗静态疲劳设计的常规方法仍然是必须考虑的因素。
关于共振频率带宽的范围,迄今尚无相关标准或规范明确界定。由式(1)可知:λ趋近于1 时β陡增即出现共振;无论η在0.001~0.01 范围内取何值,只要λ在0.71~1.22 范围内,β都大于2,否则β小于2。借鉴静强度评估中安全系数常取2 的传统做法,建议将频率比范围0.71~1.22 作为抗振动疲劳设计的共振避让区间。
4 振动疲劳评估及结构优化实例
以新研发的最高运营速度120 km/h 的铁路机车装用的扫石器及其安装系统为例,对其振动疲劳强度的评估及结构优化的过程做如下介绍。其结构如图2 所示,除了扫石器的夹木橡胶管以及各连接紧固件外,其余各部件由Q345E 级钢板焊接而成。

图2 扫石器安装结构
4.1 样车动强度试验评估及分析
试制的首台机车在京承线和京哈线进行了线路动强度试验,测得了机车各关键部位的动应力数据;再按前文所述方法计算得到各测点的等效应力,结果表明,除扫石器座上有2 个测点,图2 中的A、B 处,等效应力分别为203 MPa、163 MPa,超过相应部位疲劳许用应力90 MPa 外,其余各测点等效应力均小于疲劳许用应力。
对A、B 处2 测点的动应力数据进行时域和频域分析可知:
(1)A、B 处2 测点动应力呈现为零均值的振荡现象。
(2)A、B 处2 测点在51 Hz 附近普遍存在十分显著的应力响应。
(3)A、B 处2 测点动应力存在与速度成正比的响应频率,速度80 km/h 以上至最高试验速度132 km/h 应力波形常有拍振现象,109 km/h 时尤甚,如图3 所示,据此可推断:
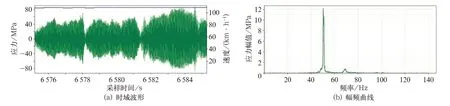
图3 速度109 km/h 测点A 应力时域和频域信号
①扫石器安装系统存在51 Hz 的自振频率。
②扫石器安装系统承受了伪随机激励(109 km/h 时频率约51 Hz,其频率与机车速度成正比)和其他随机激励。
为验证上述推断(1)的正确性,对包括扫石器、扫石器座、安装架和构架前端梁(局部)组成的结构系统建立有限元模型,如图4 所示,进行模态分析,得到250 Hz 以下的各阶模态频率和振型见表1。可见有限元分析得到的一阶频率与动应力主要响应频率仅差2.4%,由此可确认结构一阶固有频率为51 Hz。至于伪随机激励源,根据机车相关设计参数及车轮直径数据,可确认转向架轮轴驱动装置各旋转件工作转频与上述激励频率无关联;再结合我国铁路铺设规范,可确认该伪随机激励来源于按600 mm 间距铺设的轨枕。
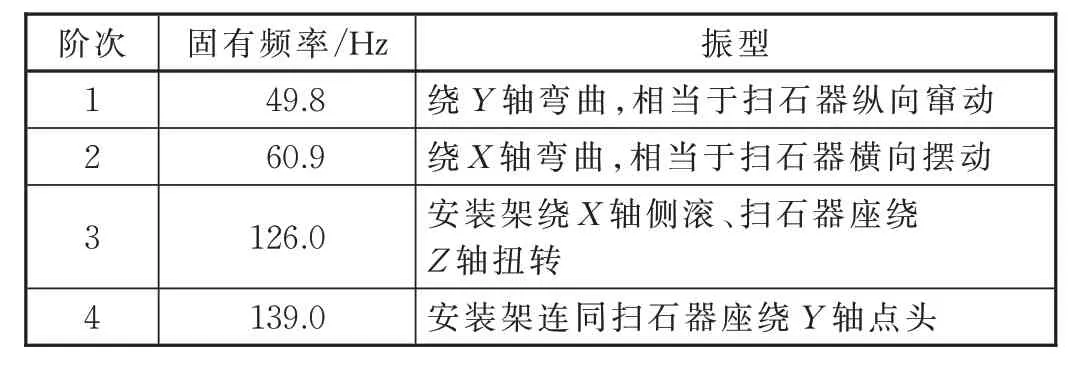
表1 扫石器安装系统模态

图4 扫石器安装系统有限元模型
综上所述,有2 个测点等效应力超过疲劳许用应力,主要原因在于较高速度下的枕跨激励频率与结构固有频率相近引起结构共振,属于振动疲劳问题。
4.2 振动疲劳强度仿真评估
为了进一步验证上述结论的正确性并了解疲劳强度分布情况,利用ANSYS 软件随机振动谱响应分析功能对图4 所示的模型进行了振动疲劳仿真评估。为了观察线路试验中测点A 处的仿真情况,在模型的相应位置也设置了标识点A。钢板母材和焊缝及热影响区材料疲劳性能数据分别参照文献[11]中FAT160 和FAT80 等级的S-N曲线确定。依次在模型的固定基础上施加垂向、横向和纵向3 个方向的加速度功率谱密度(ASD)作为激励载荷,谱的量级和频率范围按IEC 61373 标准中模拟长寿命的5 h 振幅增强谱确定,加速度谱ASD量级见表2,载荷谱频率范围如图5 所示。经仿真得到各部位的应力功率谱密度PSD,限于篇幅,仅给出了A 点在3 个ASD 激励谱下的垂向主应力PSD 曲线,如图6 所示。

表2 加速度谱ASD 量级单 位:(m⋅s-2)2⋅Hz-1
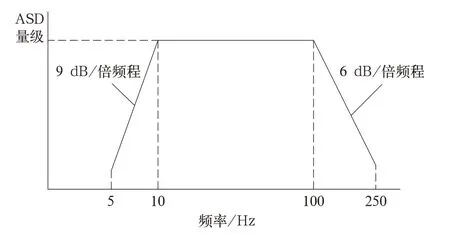
图5 载荷谱频率范围

图6 A 点垂向主应力PSD 曲线
获得应力PSD 谱后,利用Dirlik 方法计算出应力幅值概率密度,再由式(4)算出各部位在3 个载荷谱下的累积损伤DZ、DY和DX,最后求出三者之和即总损伤D,如图7 所示。其中,总损伤D大于1的部位有4 处,分别是安装架两筋板与立板垂向焊缝顶端(总损伤D分别为①10.65 和②8.04)、扫石器座主板折弯部位的顶端焊缝即A 点上方及其对称部位(总损伤D分别为③5.37 和④6.06)。
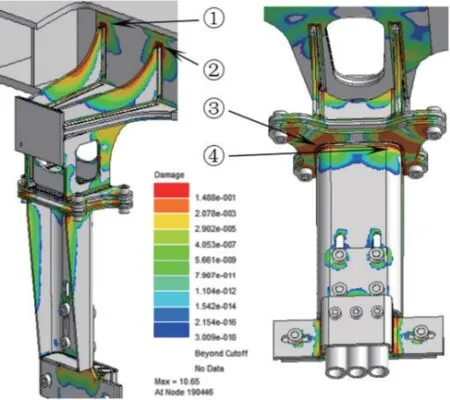
图7 累积损伤云图
仿真评估结论:按IEC 61373 标准3 个方向的振幅增强谱各加载5 h 后有多处累积损伤大于临界值1。
4.3 结构优化
根据机车适应线路条件的设计原则,结合前文抗疲劳设计和控制的有关措施,改进思路是对结构进行优化以实现:
(1)善结构件应力集中。
(2)高结构固有频率以避免轨道常见低频周期性激励引发结构共振,从而提升抗疲劳能力。
上文通过分析已识别出枕跨不平顺是机车在较高速度工况(80 km/h 以上)主要的周期性激扰能量来源,因而避免该激扰引发的共振也就成为本例一个明确的优化靶标。波长600 mm 的枕跨在机车以最高运营速度120 km/h 运行时的激励频率为55.5 Hz,依据前文提出的频率比避让建议区间(0.71~1.22),结构优化后一阶固有频率应大于78 Hz。
依据上述优化要点,在保证扫石器功能要求和构架主结构不变的前提下,采取扫石器减重、扫石器座和安装架筋板加强等措施形成了多个备选方案,通过有限元分析比选,确定的最终改进方案如图8 所示。改进方案的一阶固有频率为127 Hz,在120 km/h 以下速度时枕跨激励频率比λ将不大于0.44,符合频率比的避让建议;再对其进行振动疲劳强度仿真评估,得到的累积损伤云图如图9 所示,最大损伤为0.74,低于临界值1,满足优化目标。

图8 改进方案

图9 改进方案的累积损伤云图
4.4 改进效果试验验证
为验证改进效果,在机车左右两侧分别布置改进前后3 种方案的产品,并参照图2 和图8 所示在A、B 2 处贴应变片,这样同时进行2 种方案的动应力对比测试,规避了机车工况和线路条件的影响,所测数据更便于对比。对于改进方案,除了A、B 测点外,还在其他关键部位贴有应变片,用来全面评估扫石器安装结构的疲劳性能;另外,为方便现场更换作业,与转向架构架焊在一起的安装架未作切换,仅更换了扫石器和扫石器座,仿真得到该状态下扫石器安装系统前两阶固有频率为80.8 Hz 和102 Hz。
试验在库尔勒站—库车站区间实施。测试数据统计结果表明,改进方案各测点等效应力均小于相应部位的疲劳许用应力,满足设计要求;其中测点A 和B 的等效应力分别为34.2 MPa 和4.8 MPa,而原方案2 对照测点等效应力分别为116 MPa 和100 MPa,改进方案分别降低了70%和95%。对高速工况的应力数据分析可知:
(1)从应力波形来看,改进方案已无原方案常见的拍振现象。
(2)从频域来看,改进方案应力幅值显著降低。118 km/h 时2 方案测点A 的应力PSD 曲线100 Hz 以内,如图10 所示,可见,枕跨激励频率54.8 Hz 对应的PSD 幅值原方案和改进方案分别为122 MPa2/Hz 和1.96 MPa2/Hz,前者比后者大了61 倍;而2 方案一阶固有频率对应的幅值差异更大。这些充分说明原方案对此速度下的枕跨激励有剧烈的响应,而改进方案响应甚小。
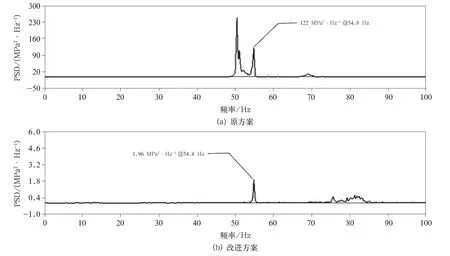
图10 118 km/h 时2 方案测点A 应力样本PSD 曲线
试验验证结论:改进方案解决了原方案的振动疲劳问题,满足使用要求。
5 结 论
(1)针对铁路车辆悬挂件振动疲劳问题,研究了仿真分析、基于随机振动谱的台架试验和线路试验等疲劳强度评估方法,以及为提高可靠性在结构抗疲劳设计和运维方面可采取的相关措施。
(2)基于单自由度系统简谐激励下稳态响应振幅放大因子的分析计算,为避免周期性激励引发共振,给出了频率比建议避让区间。基于此,对于最高速度120 km/h 的车辆,为避免轨枕枕跨激励的共振,其悬挂件固有频率应高于78 Hz。
(3)针对动应力数据的时域评估,在文献[11]和文献[15]的基础上,提出了统一的等效应力计算公式,可用于基于带拐点的S-N曲线的焊接结构的疲劳强度评估。
(4)以新型机车扫石器及其安装系统为例,介绍了振动疲劳强度评估过程、疲劳问题原因分析、结构一阶固有频率期望值的确定过程和最终优化方案,以及改进方案的验证情况;改进效果十分显著,达到预期目的,表明所提方法是有效的。
