为什么我连“解三角形”都不会?
2023-11-10徐伟东
徐伟东
浙江省象山中学 (315700)
为什么我连解三角形都不会?”这是近期听到学生抱怨最多的一句话.原本十拿九稳的“解三角形”问题,在近几年的高考、模拟考中也变得不那么容易了,与“解三角形”相关的解答题的得分率较之前普遍低了很多.在高三复习阶段,尽管进行了大量的“解三角形”的讲解与训练,但效果不甚理想,学生还是束手无策.
1、是什么让“解三角形”变得这么难?
现在的高考命题已经由“知识立意、能力立意评价”向“价值引领、素养导向、能力为重、知识为基”的综合评价转变,“优化情境设计,增强试题开放性、灵活性,减少死记硬背和‘机械刷题’现象”也已经成为了考试命题的风向标,因此,“解三角形”试题难度增加是大势所趋,具体表现在以下几个方面.
1.1 结构不良试题增加了思维量与运算量
三角形的丰富背景和广泛的应用价值决定了其成为结构不良问题的良好载体.结构不良问题往往存在问题条件或数据局部缺失或冗余、问题目标界定不明确、具有多种处理方法和路径、具有多种评估处理方法的尺度、所波及的概念、规则和原理等不确定等特性.


面对上述结构不良问题,学生首先要根据自身的认知水平,结合解题经验,对题目给定的“条件”进行甄别与选择,“条件”优劣决定解题过程的繁简程度.若学生选择的“条件”恰当,可能会很顺利完成解题任务;若学生选择的“条件”处于知识盲区之内或者不符合题目要求,就不得不重新选择新的条件进行尝试.因此,对命题者而言,相比结构良好问题,结构不良问题更能考查学生分析问题、解决问题、推理论证和运算求解能力;对学生而言,解决结构不良问题需要以敏锐的洞察力和果断的决策力为前提,而这恰恰是很多学生的短板.
1.2 条件与结论的联系不明显
解题就是寻找题目条件与题目结论之间的数学联系,它表现为沟通条件与结论的一系列演算或推理,让条件与结论相互靠近、相互转化,最终相互融合,就实现了解题的目标.所谓的容易题就是题目的条件与结论之间联系紧密,容易构建它们之间的数学关系;而难题就是题目中的条件与结论“距离”较远,需要动用一定的解题策略与运算技巧拉近“距离”,才能看清它们之间的联系.


此题条件与结论之间的“距离”看似很近,但要建立起它们之间的联系,却需要经历“弦化角——边化弦——正弦化余弦——多角化单角”等运算与推理过程,需要学生具备较强的消参与化归能力.


要成功建立本题条件与结论之间的关系,需要经历“切化弦——弦化边——三边化双边——多参变单参——确定参数的范围——求函数的值域”等运算与推理过程,与上一题相比,难度大幅度增加.

解析:这道题也是改编自2022全国I卷的高考题,与上一题异曲同工,需要经历“弦化边——切化弦——弦化边——三参变单参”等运算与推理过程,与高考原题相比,难度基本相同.
1.3 三角形中几何关系复杂化
还有很多解三角形问题并不是单纯的涉及到边与角之间的关系,而是引入新的几何量,比如,中线、高线、角平分线、重心、内心、外心等,使三角形形成了一系列新的几何关系,从而导致条件与结论之间的“距离”更加疏远,解题方法也变得多样,解题思路更难把握.


例6 (2021全国I卷)记ΔABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asinC.(1)证明:BD=b;(2)若AD=2DC,求cos∠ABC.


图1
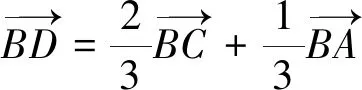
2、如何让学生学会解“解三角形”?
2.1 领会“变与不变”的命题观
高考命题不变是相对的,变是永恒的,尤其在“一核”“四层”“四翼”的高考评价体系下,以批判性思维为代表的关键能力成为了高考命题的主要方向和要求,关于“解三角形”的命题只会更加变化多端,通过大量刷题来提升解题的能力的招数不再有效;“解三角形”不一定被定格在高考解答题的“第一题”,不一定属于“容易拿分的题”,学生不会做可能是“正常的事”.
虽然我们无法把控试题形式和难度,但解决“三角形”问题的两个工具和三大思想却是不变的.两大工具就是“正弦定理”与“余弦定理”,它们是解三角形的利器,可以实现边角关系的互化.三大思想指得是化归转化思想、函数与方程思想、数形结合思想.运用化归与转化思想方法,把复杂的问题转化为简单的问题,把陌生的情境转化为熟悉情境;将问题中已知的条件转化为包含边角关系的关系式,如不等式、方程或方程组和不等式组,然后通过函数或方程视角去分析问题、解决问题;若问题中涉及到相对复杂的位置关系,此时可以利用数形结合思想,将问题中复杂的逻辑关系与直观图形关联起来,充分利用其中的几何性质来实现简化运算的目的.只要灵活运用两大工具与三大思想,“解三角形”问题一般都能够迎刃而解.
2.2 坚持培养“专家思维”的教学观
为了快速提升学生的解三角形的能力,很多教师会把教学重心放在一些拓展结论的运用上,不可否认,在某些情况下,应用这些结论确实能够起到事半功倍的作用.


但这些结论的适用范围有严格的限制,比如,例6同样满足“张角定理”模型,但“张角定理”的结论对它基本没什么用.不仅如此,这些拓展性的结论从发现到证明、到运用,到被纳入到认知结构中,期间需要经历一个比较长内化的过程,学生未必能够真正掌握.因此,“解三角形”一方面应该立足通性通法,另一方面应该把教学重心放在培养学生的“专家思维”上,即让学生学会像专家那样能够对数学问题作出快速而准确的判断,并在洞悉问题本质的基础上提出解决问题的方案.
如何培养“专家思维”?首先要重视概念的再认知,不仅要让学生数量掌握常用的公式与定理,还要探究它们之间的关联性,例如,正弦定理与余弦定理本质上是一致的,可以从正弦定理推出余弦定理,反之也成立;正弦定理与余弦定理是圆的性质的三角表征,也就说能够利用圆的性质来推导这个两个定理;余弦定理是勾股定理的推广,那么能否像推导勾股定理那样推导余弦定理?经历概念再认知的过程有助于学生加深对核心概念的理解,能强化知识与现象、与情境的关联程度.其次,立足波利亚的解题四步曲 “理解题目——拟定方案——执行方案——回顾总结”来提炼针对不同类型三角形问题的解题思路与研究视角,例如,对于“取值范围问题”,可以选择从“三角形中的不等关系、三角形解的个数、函数值域、基本不等式”等4个视角来求取值范围;对于“面积问题”,可以采用“执果索因”的办法,先把面积用边、角等基本量表示出来,然后在通过化归、消参实现对问题的转化,从而能够保证学生根据解题的实际需求,熟练调用相关的解题策略.
