考虑流固耦合的装配式管线水击压力波速计算研究

陈明，梁泽山，彭小庆，许亚能，付江华

(1.重庆赛宝工业技术研究院有限公司，重庆 401332；2.重庆理工大学车辆工程学院，重庆 400054)

0 前言

装配式管线由进出口两端均带有卡槽的钢管、管路附件以及各种配套设备组合装配而成，具有机动灵活、展收迅速、维修方便等优点，已经在化工工业、农业灌溉、市政工程以及军事后勤保障，尤其是油料应急输送保障等领域得到了广泛的应用[1]。

在管输过程中，水击是经常出现的一种瞬态工况，严重时会导致超常压力脉动，在流固耦合作用(Fluid-Structure Interaction，FSI)下将进一步诱发管道结构振动甚至破坏，因此应该进行全面地分析、预防和控制[2-4]。水击压力波速是水击分析中非常重要和敏感的参数，受到流体压力、温度、含气量以及管道结构尺寸、管端约束形式、管材等多种因素的综合影响。准确计算管道水击压力波速一直是水击分析领域的热点。

周云龙等[5]分析了含气量对浆体水击过程的影响，提出了复合管道气液固三相流的浆体水击波速计算公式。吴迪等人[6]提出了内置软管的水平管道水击波速公式，并对影响水击波速的因素进行了敏感性分析。奚斌等人[7]针对环形断面管道的结构特点和流体运动特性，推导了环形断面管道水击波速的计算公式，并分析了液流摩阻项对公式的影响。WAN和 MAO[8]基于等效弹性模量法，提出了一个适用于钢丝骨架复合型PE管的水击波速计算式，并分析了钢丝骨架对瞬变响应过程的影响。史富全[9]综合考虑了井筒流体含气率、气液两相流型、固相类型等对水击波速的影响，推导了水击波在气、液、固三相混合流体中传播速度计算公式。郭强等人[10]在薄壁管流固耦合模型的基础上，建立了适用于厚壁管流固耦合分析的一维数学模型，并研究了管道不同厚径比对压力波速与应力波速的影响。REZAPOUR和 RIASI[11]以不同浓度的聚丙烯酰胺溶液作为黏弹性流体，在铜管和聚乙烯管中，分别研究了流体的黏弹性对水击压力波的衰减以及波周期的影响。LI等[12]对液体火箭推进剂输送管道中的低温冷凝两相流压力波传播问题进行了研究，深入分析了流体压力波的传播与衰减对不稳定频率的依赖关系。KUBRAK和KODURA[13]研究了在管道中分别置入薄壁圆管、厚壁圆管以及实心圆管时的水击压力波速计算方法，并通过进一步分析认为内置低体积弹性模量的圆管可对水击过程产生阻尼效应。胡晓东等[14]搭建了水击压力波试验系统，对4种水击压力波速计算方法进行了研究与对比，以平均值、标准差和变异系数为指标，分析了4种波速计算方法的数值结果与稳定性。

综上，目前对管道水击压力波速的研究主要集中在管输介质、管壁材料、管道截面形状等因素对波速的影响，而有关管道连接方式对波速的影响研究却鲜有见到。装配式管线各管段、管件之间均采用连接器加胶圈的连接结构，密封胶圈的弹性模量远小于钢材，两者相差105数量级。装配式管线上数量众多的密封胶圈必然会改变整条管线的弹性模量，从而对水击波速产生明显影响。虽然蒲家宁[15]、蒋明等人[16]研究了装配式管线中密封胶圈对水击响应的影响，但均未计及管线系统中的FSI效应。鉴于实际管线系统中存在流体与管路结构的耦合互动作用，考虑FSI效应的水击响应更符合实际情况。因此，本文作者对装配式管线中的耦合水击波速计算方法进行研究，以期进一步为准确地分析装配式管线系统耦合水击响应奠定基础。

1 流固耦合水击动力学模型

在管道水击分析研究领域常采用薄壁管假设，以此可忽略径向应力的影响。但在实际的管输系统中，有时难以界定究竟是薄壁管还是厚壁管。因此，文中不做薄壁管假设。考虑流体与管道之间的耦合互动效应，耦合水击动力学模型[17]可表示为

(1)

(2)

(3)

(4)

式中：v为流体流速；p为管内流体压力；U为管道平均轴向振速；σ为管壁平均轴向应力；K为流体体积弹性模量；Ep为管材的弹性模量；μp为管材的泊松比；D为管道内直径；e为管壁厚度；ρf为流体密度；ρp为管材的密度；g为重力加速度；θ为管道倾角；x为管道轴向；t为时间。

上述FSI四方程模型属于拟线性双曲型偏微分方程组，其特征方程具有4个不相等的实根，即考虑FSI效应的水击波速Cf和轴向应力波速Cp：

(5)

(6)

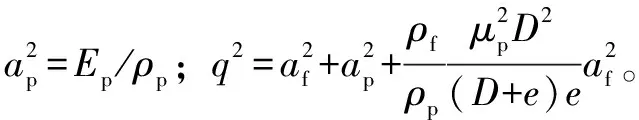
从式(5)(6)可以看出，考虑FSI效应时，耦合水击波速与经典水击波速及轴向应力波速均相关，而管材弹性模量Ep则是决定水击波速和轴向应力波速的重要参数之一。密封胶圈的存在必然会改变整条装配式管线的弹性模量，进而对耦合水击波速造成影响。

2 考虑密封胶圈影响的耦合水击波速计算

2.1 密封胶圈的形变分析

装配式管线各管段、管件之间由卡箍式连接器连接、胶圈密封，其连接结构如图1所示。当受压液体充满胶圈内的环形槽时，胶圈膨胀并紧紧地贴在管子卡槽的凸缘上，起到密封作用。

图1 连接器(a)、胶圈(b)及连接结构(c)示意

根据图1(c)所示的连接结构，密封胶圈微元段的受力情况如图2所示。

密封胶圈受到管内流体压力p作用产生形变。在Z方向上(即胶圈圆周方向)，胶圈微元段因泊松效应而伸长，但变形受到连接器的约束，产生挤压力pZ。胶圈在三向应力的作用下，体积Vr将发生变化，从体积变化量ΔVr相等的角度，可将胶圈形状及受力状态简化，如图3所示。

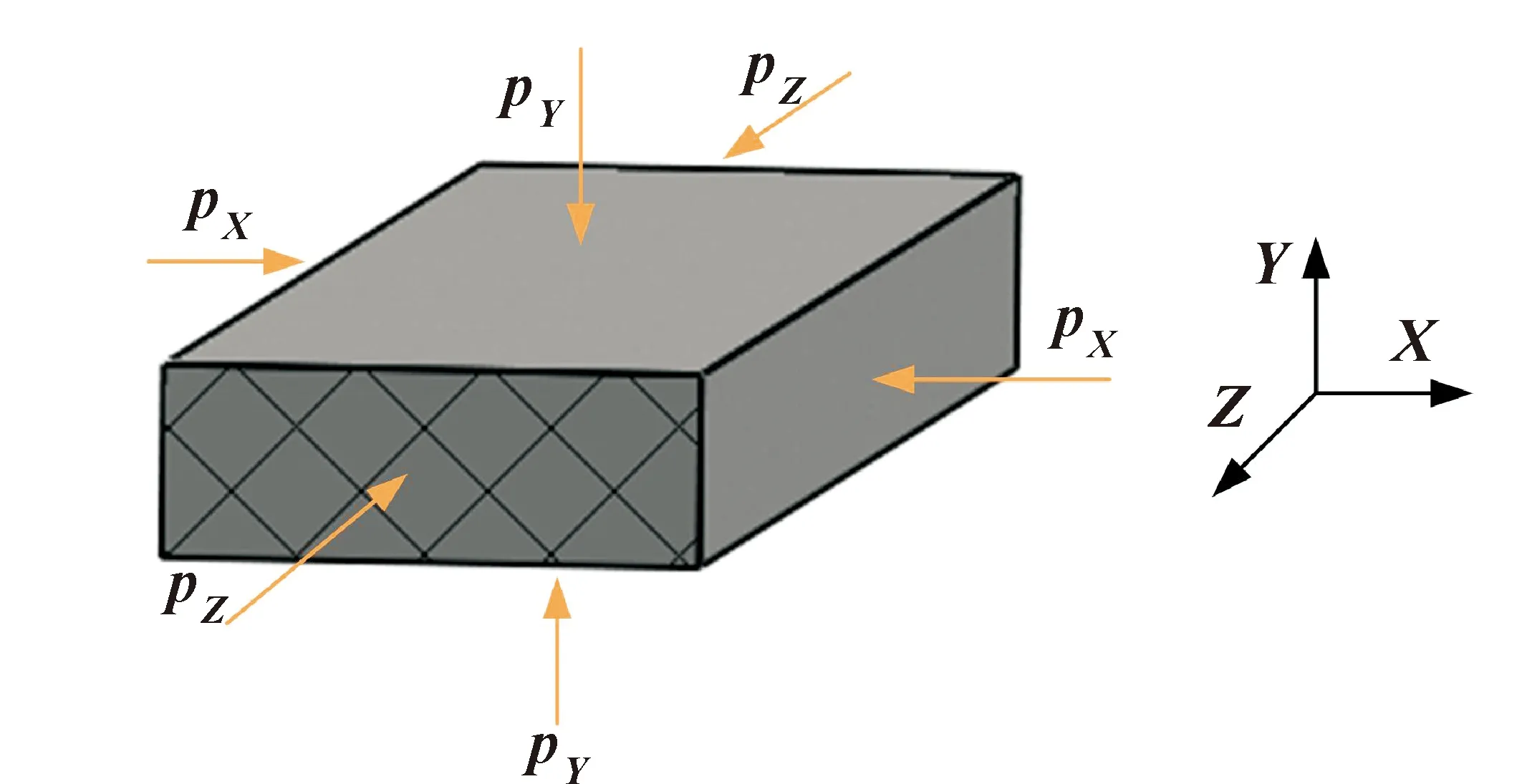
图3 胶圈当量体及受力状态

密封胶圈由丁腈耐油橡胶制成，不是线弹性材料，但在小变形范围内可近似认为其满足虎克定律，应力与应变成正比。由广义虎克定律可知，在三向应力状态下，各方向的线应变[17]分别为

(7)

(8)

(9)

式中：Er为橡胶的弹性模量；μr为橡胶的泊松比；x、y、z分别为胶圈微元段的宽度、厚度、长度；Δx、Δy、Δz分别为胶圈微元段的宽度增量、厚度增量、长度增量；σX、σY、σZ分别为X、Y、Z方向上的应力。

值得注意的是，由于胶圈对连接器的挤压，连接器也会发生一定程度的变形。但连接器厚度较大且外侧有加强筋，故强度和刚度都很大，可近似为刚性体，不产生形变。这样，胶圈在Z方向无法发生伸长，即Δz=0。

在压力作用下，胶圈的体积应变为

(10)

忽略二阶微量，则式(10)变为

(11)

由式(9)及Δz=0可得：

σZ=μr(σX+σY)

(12)

将式(12)和σX=σY=-p代入式(11)得：

(13)

该式即为胶圈受液体压力后的体积压缩量。

2.2 考虑密封胶圈影响的水击压力波速

先考虑一根管子和一个胶圈的情形，两者长度分别为Lp和Lr。管道末端突然关阀引发水击。假定管道内初始流速为U0，关阀后的最终流速为U1，则Δt=(Lp+Lr)/af时间内流入(Lp+Lr)管段内的流体体积为

Vf=(U0-U1)(AfLp+ApLr)/af=

ΔU(AfLp+ApLr)/af

(14)

式中：Af为管道内截面积；Ap为管道外截面积。

钢管在流体压力p作用下，其径向膨胀量ΔD为

(15)

则单根钢管的容积变化量ΔVp为

(16)

由于胶圈受到连接器约束，因此胶圈段被压缩导致的体积减小量就等于其容积的增加量ΔV′r，即：

(17)

根据连续性原理，流入的流体量等于流体、胶圈的体积压缩量和管道容积膨胀量之和：

Vf=ΔVf+ΔVp+ΔV′r

(18)

式中：ΔVf为流体的体积压缩量；ΔVf=p(AfLp+ApLr)/K。

将式(14)(16)(17)代入式(18)可得：

(19)

将惯性水击压力表达式ΔU=p/(ρfaf)代入式(19)，即可得计及密封胶圈影响的经典水击压力波速计算式：

(20)

上述的推导是基于一根管子和一个胶圈的情形。若推广到整条管线，设全线共有管子np根，密封胶圈nr个，则水击压力波速计算式为

af=

(21)

式中：α=(AfLp+βApLr)；β=nr/np。

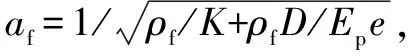
将式(21)代入式(5)，则可得到考虑密封胶圈影响的装配式管线耦合水击波速计算公式。

3 验证与分析

3.1 试验验证

试验管道系统由室内管道、室外环形管道、电动泵、控制阀以及数据采集设备等组成，如图4所示。

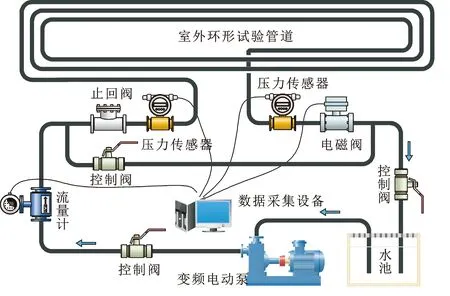
图4 试验管道系统示意

因为受实验场地限制，试验管道较多地使用了短管和弯头，单管段平均长度按4 m计。各管段、管件之间的连接方式为卡箍式连接，胶圈密封。变频电动离心泵将清水从水池抽吸到试验管道中循环输送。当管内流动达到稳定状态时，控制电磁阀突然关闭(或关闭一定时间后突然开启)产生水击工况。压力传感器量程为0～5.0 MPa，精度等级为0.2级，频率响应为10 kHz。上、下游压力传感器之间的管道总长度L为656 m，分别采用周期法与波前法测量水击波速值。试验管道系统的主要参数见表1。

表1 试验管道系统主要参数

当稳态流量达27.9 m3/h时，发出关阀信号使电磁阀瞬间关闭，获得水击压力响应波形如图5所示。根据水击周期法，若水击压力振荡周期为T，则水击压力波速af=4L/T。经3次重复试验，测得试验数据如表2所示。

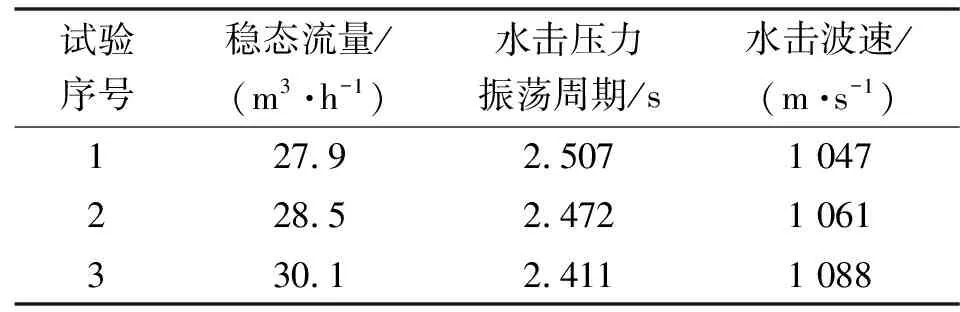
表2 瞬间关阀的水击试验数据(周期法)

图5 瞬间关阀的水击压力响应曲线

当稳态流量为30.1 m3/h时，先将电磁阀关闭一段时间后再突然打开，记录减压波压力波前变化曲线，如图6所示。

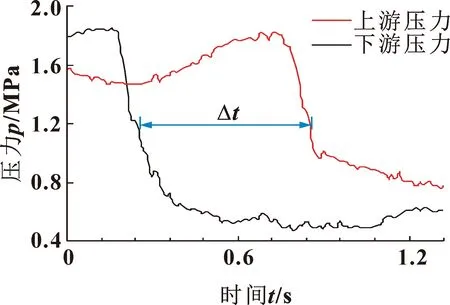
图6 瞬间开阀的减压波前曲线

根据水击波前法，若上、下游2个压力传感器检测到压力波前到达的时间差为Δt，则水击压力波速af=L/Δt。同样进行3次水击试验，试验数据如表3所示。

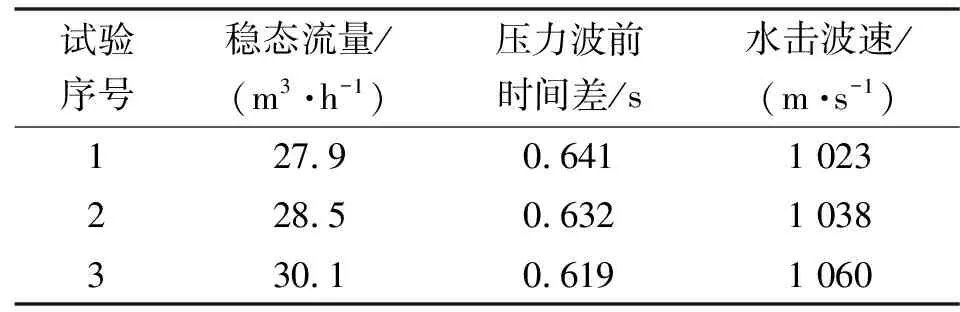
表3 瞬间开阀的水击试验数据(波前法)

按表1中的参数值，分别采用文中提出的方法和Korteweg式进行水击压力波速计算，并与试验实测值进行对比，如表4所示。

表4 水击波速计算值与试验实测值对比

由表4可知：水击波速实测平均值在1 040～1 065 m/s之间，明显小于Korteweg式的经典水击波速计算值。这说明装配式管线的连接结构对水击响应具有一定的阻尼效果，密封胶圈的存在对水击波速起到了明显的衰减作用。文中方法计算值与试验实测值吻合得较好，说明文中方法是正确可行的。相比不考虑FSI效应而言，考虑FSI效应的耦合水击波速计算值更接近试验实测值，表明管道结构运动和变形对流体压力波动响应的影响是不容忽视的。

3.2 密封胶圈对不同输送介质中水击波速的影响

当装配式管线分别输送清水、汽油和柴油时，采用文中方法进行水击波速计算。管道参数见表1，汽油密度为730 kg/m3，体积模量为916 MPa；柴油密度为840 kg/m3，体积模量为1 410 MPa。根据上述参数，不同输送介质中的水击波速计算值如表5所示。

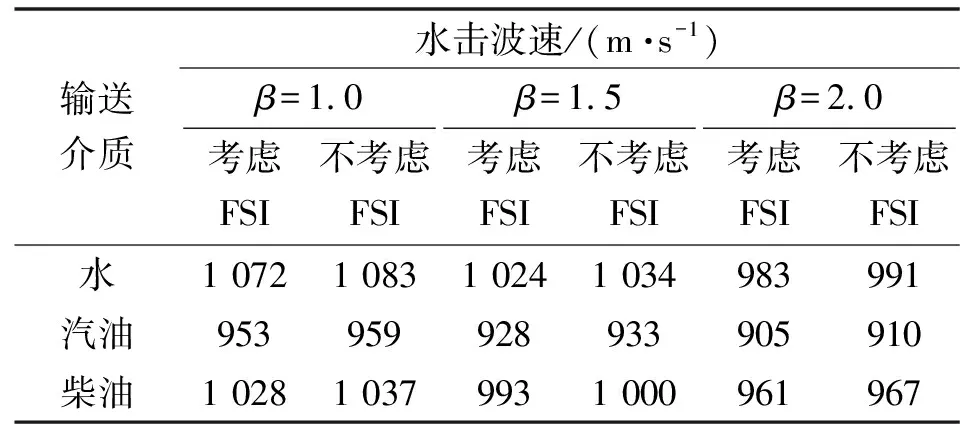
表5 不同输送介质中的水击波速计算值

表5中β=1.0是装配式管线系统中短管件数量少、可忽略不计的情况，若不可忽略时，则β>1.0。从表5可知：密封胶圈对水击波速的衰减程度随着其数量的增多而增大。在不同输送介质中，考虑FSI效应的耦合水击波速值均小于经典水击波速值，这是因为在流固耦合作用下，流体的部分水击压能转换成了管道结构的振动能量，导致流体水击波速有所降低。

图7所示为密封胶圈对不同介质中水击波速衰减率的变化趋势对比曲线。图中的波速衰减率是指不计密封胶圈影响的波速与计及密封胶圈影响的波速之差的百分数。

图7 密封胶圈对水击波速的衰减率曲线

从图7可以看出：当考虑FSI效应时，密封胶圈对水击波速的衰减作用均比不考虑FSI效应时小。对3种不同输送介质而言，密封胶圈对水中的水击波速衰减率最大，柴油次之，汽油最小。这主要是因为水的体积模量最大，最不容易被压缩，此时密封胶圈的弹性则体现得最明显，因而对水中水击波速的衰减作用也最显著。

3.3 管道不同厚径比对水击波速的影响

分析装配式管线不同厚径比e/D对水击波速的影响，输送介质为清水。为了显示文中方法与薄壁管水击波速模型的区别，对式(21)按薄壁管假设进行简化，可得计及胶圈影响的薄壁管经典水击波速表达式：

(22)

将式(22)代入式(5)则得到计及密封胶圈影响的薄壁管耦合水击波速计算式。

图8展示了在不同密封胶圈数量下，耦合水击波速随管道厚径比的变化情况。

图8 管道厚径比对耦合水击波速的影响

从图8可以看出：在相同厚径比条件下，采用文中方法的水击波速计算值均小于薄壁管模型计算值，这与文献[17]中的相关结论一致。薄壁管模型假设管壁轴向应力沿径向为常数，而文中方法基于厚壁管模型，考虑了管壁轴向应力沿径向变化的实际情况，采用的管壁截面轴向应力平均值小于管内壁与流体交界面处的轴向应力，因此计算得出的耦合水击波速值也相对较小。当e/D<0.05时，文中方法与薄壁管模型的波速计算值相差小于5%，此时采用文中方法或薄壁管模型均是可行的；当e/D≥0.05时，采用文中方法进行计算则更为可靠。

(23)

这是由于装配式管线采用连接器连接，各管段接头之间存在轴向间隙。每个间隙与外侧的密封胶圈之间均形成了环状空腔结构，可吸收水击能量，在水击过程中担任着“水击压力缓冲环”的角色，能对水击波速起到明显的衰减作用。当e/D小于某值时，管道尚属薄壁管范畴，虽然e/D增加，但其环状空腔体积增量较小，不足以抵消由于管壁增厚、管道径向膨胀量减小对水击波速带来的增速效果，因此水击波速呈暂时增加的趋势。当e/D超过某值时，随着e/D增加，环状空腔体积增量对水击响应的衰减作用逐渐占据主导地位，从而导致水击波速持续降低直至极限值。

4 结论

装配式管线中含有大量密封胶圈，对全线水击响应的影响显著。文中在考虑FSI效应的基础上，分析了密封胶圈在水击压力下的形变情况，提出了装配式管线耦合水击压力波速的计算方法。采用水击试验系统对文中方法进行了试验验证，并分析了密封胶圈和管道厚径比对水击波速的影响，得出如下结论：

(1)试验实测值与文中方法计算值吻合较好，表明文中方法适用于装配式管线水击波速的预测计算与分析。其中，考虑FSI效应的水击波速计算值更接近实测值，说明对装配式管线系统的水击响应分析应考虑FSI效应的影响。

(2)密封胶圈对水击波速起衰减作用，衰减率随其数量的增多而增大。当考虑FSI效应时，密封胶圈对水击波速的衰减作用比不考虑FSI效应时小。管道内输送介质的体积模量越大，密封胶圈对水击压力波速的衰减作用越明显。

(3)文中方法基于厚壁管模型，当e/D<0.05时，文中方法的水击波速计算值与薄壁管模型计算值相对偏差较小；当e/D≥0.05时，采用文中方法进行计算则具有更高的可靠性。装配式管线各管段之间的连接部位形成了具有吸收水击能量效果的环状空腔结构。随着e/D的增加，环状空腔对水击响应的衰减作用逐渐凸显出来，因此管内水击波速呈现短暂增大后又持续减小的变化趋势。