电液四缸位置伺服系统同步控制策略研究
2023-11-09段国元杜厚羿黄华饶俊森王勇敢张兵
段国元,杜厚羿,黄华,饶俊森,王勇敢,张兵
(1.镇江市流体传动与控制重点实验室,江苏镇江 212013;2.丹佛斯动力系统(江苏)有限公司,江苏镇江 212013;3.江苏大学机械工程学院,江苏镇江 212013)
0 前言
电液多缸同步系统具有功重比高、响应快、控制精度高等显著优点,因此被广泛应用于国防科技[1]、矿山机械[2]和工程机械[3]等领域。国内外学者针对多缸同步控制策略进行了大量研究。周强等人[4]基于交叉耦合的思想提出了一种双模糊PID跟踪控制器,相比普通模糊PID控制,该控制策略能够明显减小偏载情况下双缸同步系统的同步误差。YANG等[5]提出一种交叉耦合预补偿解耦控制器,以削弱并联液压机器人系统的动态耦合效应。然而,传统交叉耦合控制仅适用于双轴同步控制系统[6-7]。因此,葛育晓、赵荣珍[8]在偏差耦合控制的基础上,设计了积分滑模跟踪控制器,与传统并行同步控制对比,该控制策略有更好的抗扰动能力。LI等[9]采用基于平均偏差耦合的二阶自适应滑模控制方法实现对多电机的同步控制,相较于传统偏差耦合控制,该控制策略结构上更加简单,鲁棒性更强。吴翠红、郝芯[10]针对多激振器的同步控制问题,采用了自适应滑模和相邻交叉耦合相结合的控制策略,仿真结果表明:该策略能有效提高激振器同步系统的精度。PI等[11]为实现对六自由度液压并联机器人的同步跟踪控制,采用具有内/外环控制结构的串级控制方法,并将相邻交叉耦合思想引入同步控制中,实验结果表明:该控制策略能使并联机器人中各关节同步运动。
本文作者针对四缸位置伺服系统,提出一种相邻交叉耦合方法和自适应鲁棒控制相结合的控制策略。为减小时变参数和不确定性对系统的影响,单缸控制器采用自适应鲁棒控制器,然后基于相邻交叉耦合思想设计PID耦合控制器,以减小同步误差。
1 单缸轨迹跟踪控制器设计
将活塞初始工作位置选在中位,选取状态变量为
x=[x1,x2,x3]T=[y,y,A1p1-A2p2]T
(1)
则系统模型状态空间方程为
(2)
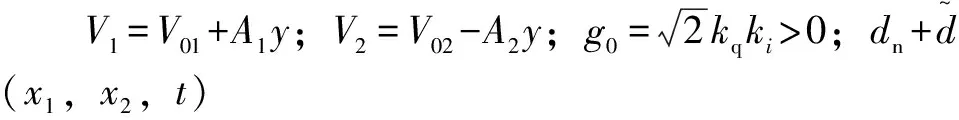
(3)

(4)
(5)
式中:θmin=[θ1min,θ2min,θ3min,θ4min]T、θmax=[θ1max,θ2min,θ3max,θ4max]T分别为系统未知参数的上下界。式(2)可以改写为
x1=x2
mx2=x3-θ1x2-θ2Sf(x2)-θ3-mg-
x3=g1u-fb-θ4fp
(6)
式中:
(7)
定义系统的误差变量为
e1=x1-x1d
(8)
e2=x2-α1
(9)
e3=x3-α2
(10)
定义系统变量和不确定参数的估计误差为
(11)
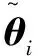
1.1 求解虚拟控制量α1
定义李雅普诺夫函数V1为
(12)
对V1进行求导:
(13)
由于式(6)中第一个状态方程里不含有时变参数和不确定性,可以设计:
(14)
式中:k1为正的反馈增益,将式(14)代入式(13),得:
(15)
将式(14)代入式(9),有:
(16)
对上式进行拉普拉斯变换:
(17)
由经典控制理论可知,该传递函数是稳定的,当e2→0时,必能得到e1→0。此外,由式(16)中可以看出,e2中不仅包含位置跟踪误差,同时还包含了速度跟踪误差,当e2趋于零时,系统的速度误差也是收敛的,因此,接下来以e2收敛于零为设计目标。
1.2 求解虚拟控制量α2
定义李雅普诺夫函数V2为
(18)
对V2进行求导:
(19)
将式(2)、(15)代入式(19)可得:
(20)
所设计的虚拟控制量α2具有如下的结构形式:
α2=α2a+α2s1+α2s2
α2s1=-k2s1e2
(21)
将式(21)代入式(20)
(22)
式中:φ2为不确定参数估计误差的系数矩阵,φ2=[-x2,-Sf(x2),-1,0]T;k2s1为正的控制器设计参数;α2a为模型补偿项;α2s1和α2s2为系统的鲁棒反馈项,其形式均为误差e2的比例反馈。α2s2还需满足如下的正定条件:
(23)
ε2为正的任意小的正数,设计α2s2为
(24)
其中:k2s2>0为控制器设计参数;θM=θmax-θmin。将式(23)、(24)代入式(22)可得:
(25)
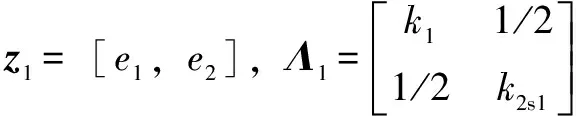
1.3 求解控制器u
定义李雅普诺夫函数V3为
(26)
对V2进行求导:
(27)
将式(6)中第3个方程代入
(28)
式中:
(29)
u=ua+us1+us2
us1=-k3s1e3/g1
(30)
将式(29)(30)代入式(28),可得:
(31)
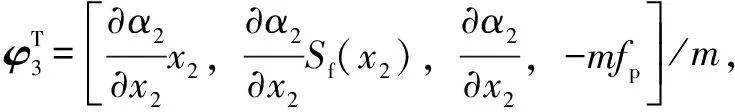
(32)
ε3为任意小的正数,可以设计us2为
(33)
k3s2为正的控制器参数,将式(32)(33)代入式(31)得:
(34)
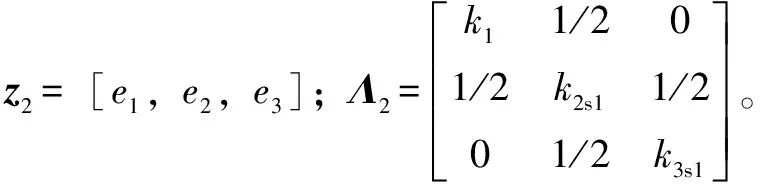
1.4 自适应率设计
与基于反步法的自适应率相比,文中采用的自适应率基于不连续映射,该方法能够将自适应控制器和鲁棒控制器分离开来,减少二者之间的耦合,使控制器结构简洁,减小了控制器的计算量。
(35)
参数自适应律设计为
(36)
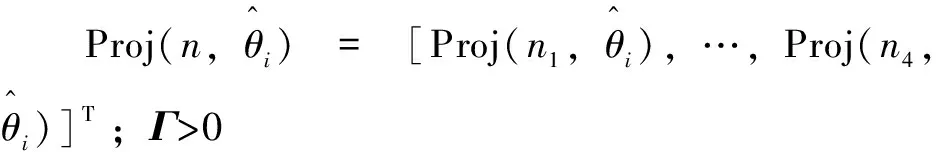
(37)
1.5 系统稳定性分性
假设系统只存在参数不确定性,系统的李雅普诺夫函数定义为
(38)

(39)
式中:λmin(Λ2)为正定矩阵Λ2的最小特征值。W∈L2,W∈L∞,根据Barbalat引理可知,当t→∞,W→0,系统是渐进稳定的,结合式(17)的分析可知,误差e1、e2、e3以及参数估计误差均渐进收敛于零。
2 同步控制器设计
对于四缸同步控制系统,定义第i个缸的轨迹跟踪误差为
ei=xi-xd(i=1,2,3,4)
(40)
式中:xi为第i个液压缸的实际位移;xd为同步系统中各缸的参考位移。在四缸同步系统中,除了要保证各液压缸轨迹跟踪精度,即ei→0,当四缸完全同步时,各液压缸的轨迹跟踪误差还需要满足:
e1=e2=e3=e4
(41)
在实际工作过程中,如干扰、偏载等众多因素会影响系统的同步精度,因此不仅要考虑各通道跟踪误差,还需要考虑各通道之间的同步误差。根据相邻交叉耦合的原理,每个液压缸除了需要考虑自身的跟踪误差外,还需考虑相邻的2个液压缸的跟踪误差,因此可以定义四缸同步系统的同步误差为
(42)
分析上式可以得知,若能够保证εi→0,则可以满足式(41),从而实现四缸的同步控制。四缸同步控制框图见图1。
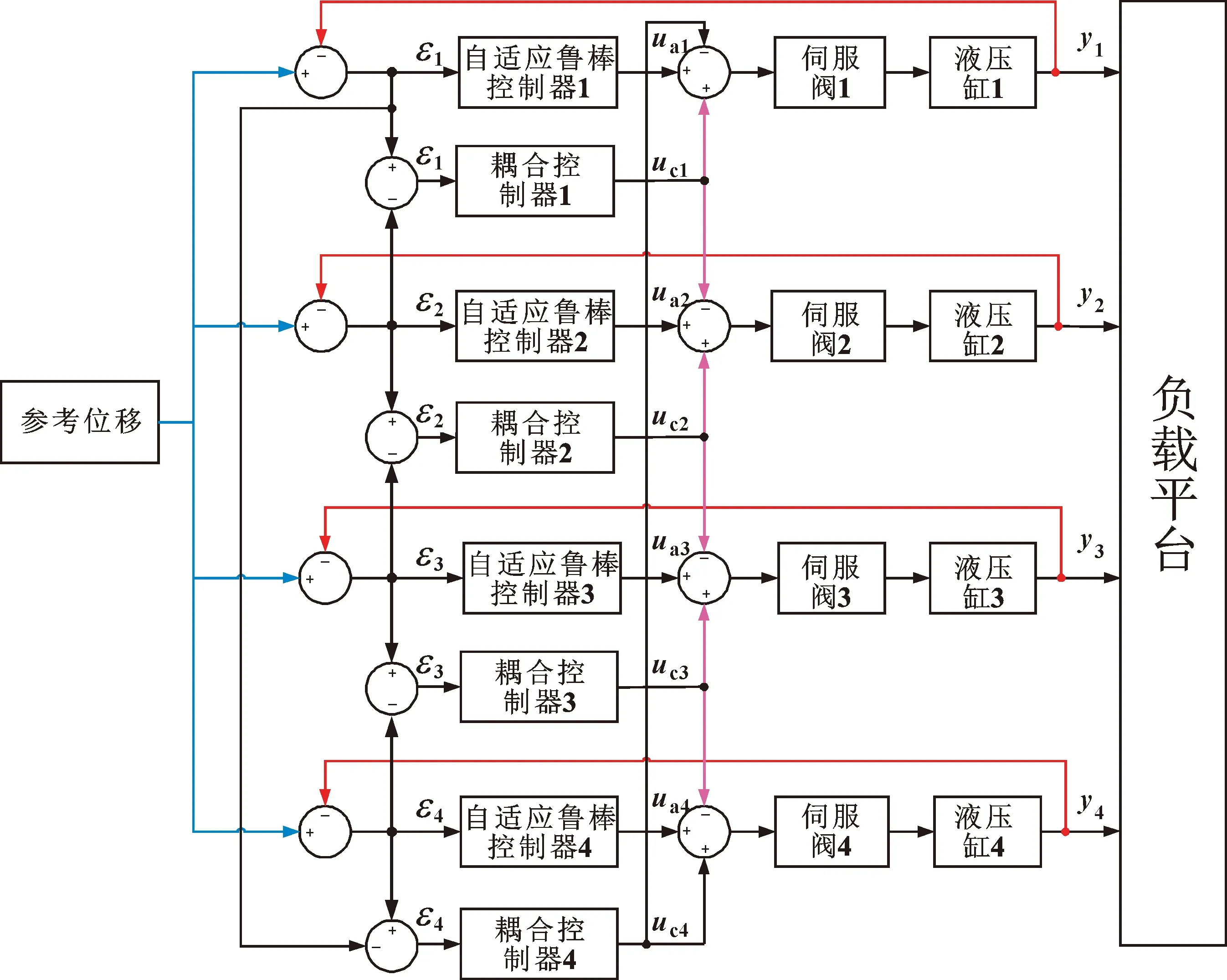
图1 四缸同步控制框图
3 仿真分析
利用MATLAB/Simulink对所设计的控制器进行仿真分析,其中相关仿真参数见表1,PID耦合控制器的参数设置为Kp=1 500,Ki=0.2,Kd=0.1。
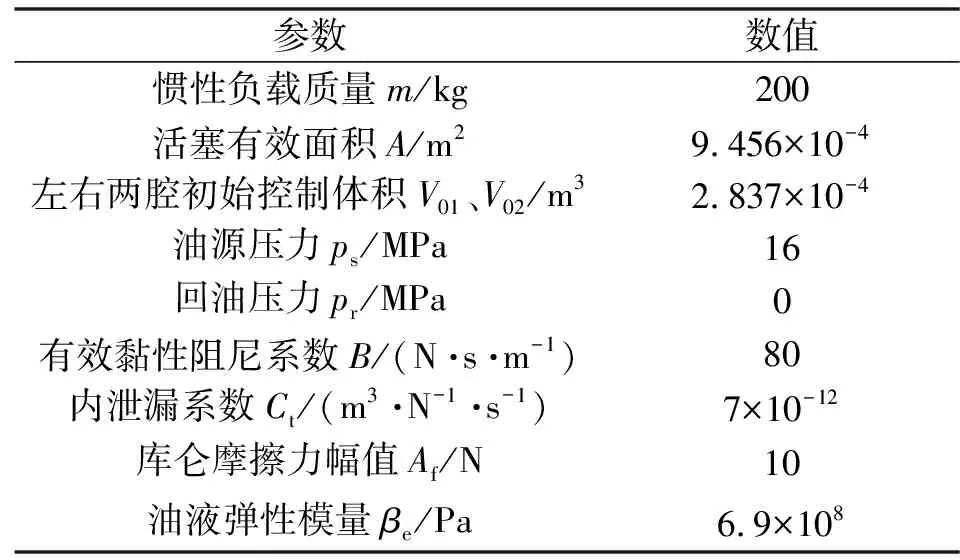
表1 仿真参数
3.1 正弦响应分析
图2、图3和图4分别为跟踪给定幅值为80 mm、频率为0.25 Hz时四缸的位移响应曲线、跟踪误差曲线和同步误差曲线。图中,稳态时单缸的最大轨迹跟踪误差为0.3 mm,稳态跟踪精度为0.38%。从图中可得,四缸最大同步误差为0.33 mm,最大稳态同步误差为0.05 mm,同步精度可达0.06%。

图2 跟踪yd=80 sin(0.5πt)mm四缸位移曲线

图3 跟踪yd=80 sin(0.5πt)mm四缸误差曲线

图4 跟踪yd=80 sin(0.5πt)mm四缸同步误差曲线
3.2 有偏载时同步性能分析
为分析偏载工况下系统的同步性能,为每个液压缸设置200~300 N随机变化的负载力,仿真结果如图5—7所示。从图6和图7中可以看出:系统存在偏载时,单轴的最大稳态跟踪误差为-0.72 mm,较没有偏载时增加了0.42 mm,稳态跟踪精度为0.9%,较无偏载时下降了0.52%。稳态时四缸的最大同步误差为-0.1 mm,比没有偏载时增加了0.05 mm,同步精度下降了0.04%。由此可见,当系统存在偏载现象时,虽然系统的单轴位置跟踪精度和同步精度均有不同程度的下降,但所设计的控制策略仍然保证了较高的同步精度,验证了所提出的控制策略的有效性。
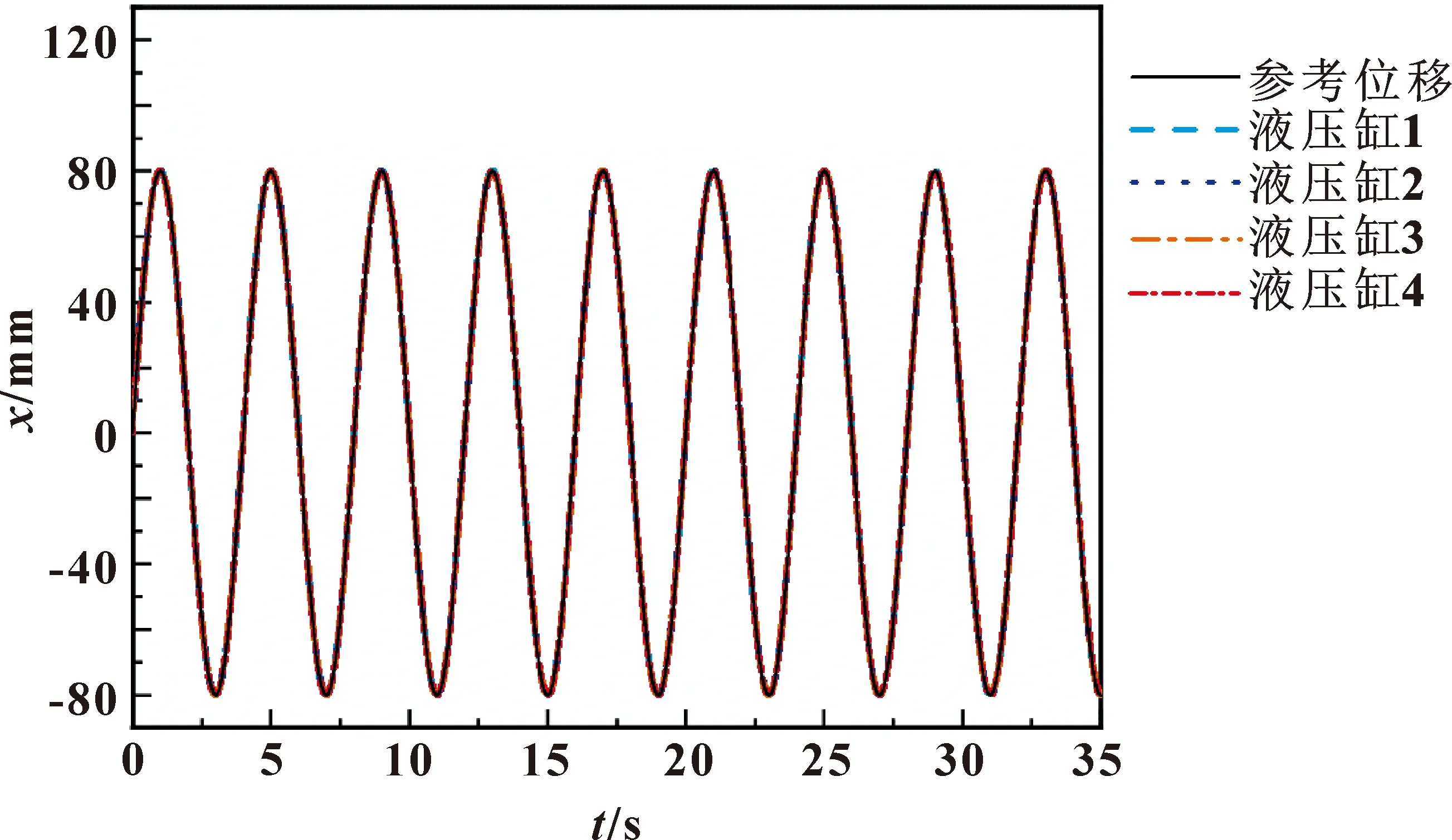
图5 有偏载时的四缸位移响应曲线
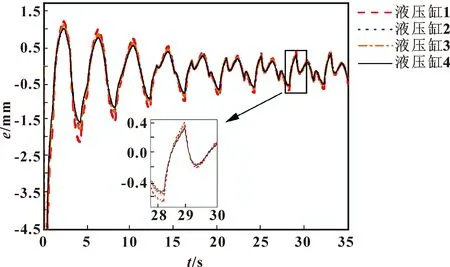
图6 有偏载时的四缸误差曲线

图7 有偏载时的四缸同步误差曲线
4 结论
文中针对四缸同步系统,提出了一种基于相邻交叉耦合的自适应鲁棒同步控制策略。在单缸采用自适应鲁棒控制策略的基础上,通过PID耦合控制器对相邻两缸的同步误差进行补偿。仿真结果表明:所设计的控制策略在有偏载和无偏载2种工况下均能够获得较高的同步精度。
