波形腹板钢箱组合梁竖向弯曲振动特性∗
2023-11-06张紫辰王根会金学军
张紫辰,王根会,王 兴,金学军
(1.青海大学土木工程学院 西宁,810016)(2.兰州交通大学土木工程学院 兰州,730070)
引言
自1986 年法国建成世界上第一座波形钢腹板组合箱梁桥——Cognac 桥以来,波形钢腹板组合梁桥在各国公路、铁路以及城市轨道交通建设领域得到了长足的发展[1-2]。然而,这种组合箱梁在正弯矩作用下,混凝土底板易出现受拉开裂的病害。为此,国内学者对传统波形钢腹板组合梁桥进行了优化,提出了采用平钢板取代混凝土底板的新型组合结构——波形腹板钢箱组合梁[3],这种结构可以充分发挥混凝土顶板抗压、钢底板抗拉以及波形钢腹板抗剪屈服强度高的优点,能够有效地解决温度应力和收缩、徐变等因素带来的病害,进一步减轻了结构自重,增大了桥梁的跨越能力[4]。同时,该类结构可进行工厂化制造和装配式施工,从而大大缩短了施工周期,因而该类桥梁具有广阔的发展前景,已在我国甘肃省中川机场T2 航站楼立交桥、彭大高速泾河特大桥等一批重点桥梁工程中得到应用。
近年来,针对波形钢腹板组合箱梁的静力特性的研究成果已在工程实践中得到了广泛的应用[5-6]。学者们也对波形钢腹板组合箱梁的动力特性进行了研究。张永健等[7]运用能量变分法推导了波形钢腹板组合箱梁桥的振动频率解析解。李鹏飞等[8]分析了不同桥墩类型对波形钢腹板连续刚构桥动力特性的影响。郑尚敏等[9]对波形钢腹板PC 组合箱梁的扭转振动频率进行了试验研究。桂水荣等[10]研究了结构参数对大跨径变截面波形钢腹板箱梁桥动力特性的影响。胡霖远等[11]将波形钢腹板混凝土梁理想化为夹心梁,基于Zig-zag 理论分析了波形钢腹板梁的自由振动特性。冀伟等[12]基于势能驻值原理得到了波形腹板钢箱-混凝土组合梁桥振动频率的简化计算方法。Feng等[13]基于Hamilton 原理,综合考虑剪切剪滞效应和界面滑移等因素,提出了一种用于计算波形钢腹板组合箱梁固有频率的改进分析方法。上述研究主要集中在波形钢腹板组合箱梁的自由振动方面,且未同时考虑铁木辛柯(Timoshenko)剪切变形、转动惯量、剪滞翘曲应力自平衡以及腹板褶皱效应等因素对结构振动特性的影响,因而具有一定的局限性。由于桥梁的弯曲振动频率是计算其冲击系数的基础,而结构在地震荷载作用下的破坏也主要源于强迫振动,所以波形腹板钢箱组合梁的动力学特性研究更为重要。
笔者基于能量变分法和Hamilton 原理,综合考虑Timoshenko 剪切变形、转动惯量、剪滞翘曲应力自平衡以及腹板褶皱效应的影响,推导出波形腹板钢箱组合梁的动力学弹性控制微分方程和自然边界条件,结合模型试验和有限元数值模拟对组合箱梁的竖向弯曲振动特性进行了精细化分析。
1 组合箱梁的振动方程
1.1 基本假定
建立组合箱梁振动方程的基本假定如下:
1)波形钢腹板具有褶皱效应,忽略其纵向抗弯作用;
2)波形腹板钢箱组合梁发生弯曲变形时,横截面纵向应变计算服从“拟平截面假定”;
3)混凝土翼板与波形钢腹板在弹性范围内协同工作,两者连接无相对滑移。
1.2 控制微分方程的建立
波形钢腹板形状如图1 所示,其有效剪切模量Gw[14]可表示为
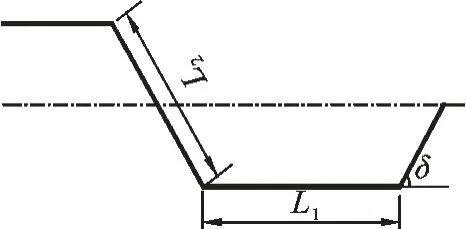
图1 波形钢腹板形状示意图Fig.1 Shape of corrugated steel webs
其中:L1为平板长度;L2为斜板长度;δ为波折角;Es为钢材弹性模量;υs为钢材泊松比。
图2 所示波形腹板钢箱组合梁由混凝土顶板、钢底板及波形钢腹板组成,其中:b2为悬臂板宽度;t1为上翼板混凝土厚度;2b1为混凝土顶板宽度;t2为钢底板厚度;h1和h2分别为顶板和底板的中心到形心轴的距离;z轴为组合箱梁的高度方向;y轴为组合箱梁的宽度方向。
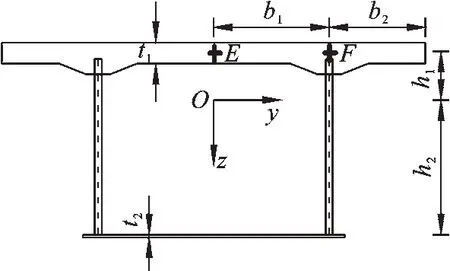
图2 波形腹板钢箱组合梁Fig.2 Box composite girder with corrugated steel webs
理论计算时,采用换算截面法将组合箱梁混凝土顶板换算为等效钢板,其等效几何材料特性为
其中:Ec为混凝土弹性模量;td为换算后等效顶板厚度;ρd为换算后等效顶板材料质量密度;ρc为混凝土质量密度。
在对称弯曲状态下设结构的跨度为l,结构的竖向动挠度为w(x,t),则剪力滞效应引起组合箱梁顶板翘曲位移η1、底板翘曲位移η2和悬臂板翘曲位移η3可分别表示为
其中:f1(y),f2(y),f3(y)分别为组合箱梁顶板、底板和悬臂板的不均匀分布函数;u1(x,t),u2(x,t)分别为结构振动时剪力滞效应引起的组合梁顶、底板和悬臂板的转角差函数;α为组合梁翼板各自满足应力自平衡条件求得的常数之和。
且有
组合箱梁顶板应力为
组合箱梁底板应力为
组合箱梁悬臂板应力为
组合箱梁顶、底板和悬臂板变形势能为
组合箱梁剪切应变能为
其中:Aw为波形钢腹板的横截面积。
组合箱梁荷载势能为
其中:M(x,t) 为x截面的动弯矩;M1(x,t),M2(x,t)分别为顶、底板和悬臂板剪力滞效应产生的动弯矩。
组合箱梁总势能为
结构总动能为
依据Hamilton 原理δ∫(T-V)dt=0[15],可得组合箱梁的振动微分方程为
相应的自然边界条件为
其中:Isy1=-∫A z[α-zf1(y)]dA;
1.3 控制微分方程的求解
根据组合箱梁的振动特点,若结构振动圆频率为ω,则有
其中:φ为组合箱梁强迫振动时的初始相位角。
由式(21)可得U(3)1和U(5)1的表达式,对式(22)进行3 次求导后将U(3)1和U(5)1代入,可得到关于U2,W和Ο的微分方程,再结合式(23)可得仅含W和Ο的微分方程。将式(20)代入并消去Ο后,可得关于W(x)的新微分方程为
对式(29)进行分析可知,其特征方程解的形式为r1,2=±(α1+iβ1),r3,4=±(α2+iβ2),r5,6=±(α3+iβ3),r7,8=±(α4+iβ4)。
根据微分方程的性质,可得式(29)的通解为
其中:n1=α1+iβ1;n2=α2+iβ2;n3=α3+iβ3;n4=α4+iβ4;C1~C8为待定常数,可由相应边界条件求得。由常微分方程组性质和恒等式原理假设Ο(x)解的表达式,结合式(20)和式(30),最终可得Ο(x)的解为
同理可得U1(x)和U2(x)的方程解为
2 边界条件
简谐均布力作用下两端简支组合箱梁边界条件为
对于两端简支组合箱梁,若跨间r点作用1 个简谐集中力Pr=P0sin(ωt+φ),且集中力Pr距左右边界距离为l1和l2,则r点需引入的连续边界条件为
其中:U下标括号内数字表示剪力滞效应引起组合箱梁顶、底板和悬臂板的转角差函数。
在求解组合箱梁的自振频率时,令均布简谐力q(x,t)=0,将式(30)~(33)或其求导式代入相应的边界条件,可以得到结构的固有频率方程,再通过Matlab 软件求解其特征值方程,从而得到结构的各阶振动圆频率ωn,将组合箱梁振动的圆频率转化成竖向自振频率,其计算式为
3 模型梁试验
为验证本研究所得波形腹板钢箱组合梁弯曲振动频率分析方法的有效性,设计制作了一跨简支组合箱梁模型,其横截面形状见图2,梁高为0.4 m,跨径为6 m,b1=0.3 m,b2=0.25 m,t1=0.05 m,t2=4 mm。组合箱梁顶板混凝土材料按照C50 混凝土设计,波形钢腹板和底板均采用Q390 钢,共设置了2 道端横隔板和3 道中横隔板,波形钢腹板厚度为3 mm,波折角δ=37°,平板长度L1=40 mm,斜板长度L2=40 mm。
采用锤击法对简支组合箱梁自振特性进行测试,采样频率为512 Hz。根据试验模型振型的分析结果,竖向拾振器布置在混凝土顶板六分点处(即L/6,2L/6,3L/6,4L/6 和5L/6 位置),敲击点避开竖向拾振器位置,试验现场照片如图3 所示,频率测试结果如图4 所示。

图3 试验现场照片Fig.3 Photo of test site
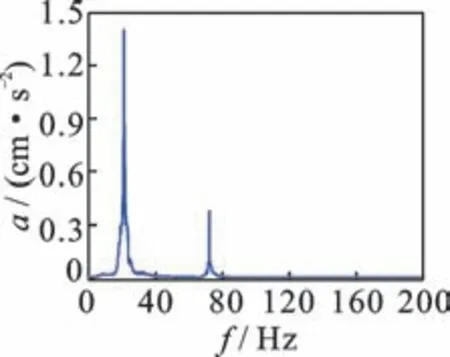
图4 频率测试结果Fig.4 requency test results
4 有限元模型
采用ANSYS 15.0 软件建立波形腹板钢箱组合梁的有限元模型,如图5 所示,其中混凝土采用SOLID65 单元模拟,波形钢腹板选用SHELL63 单元模拟,同时增加目标单元TARGE170 和接触单元CONTA175,以实现钢混连接部位的多点耦合接触,这样可对顶、底板和腹板独立划分网格,从而保证了模拟的精度。
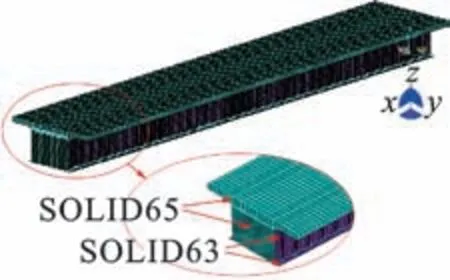
图5 有限元模型Fig.5 Finite element model
5 对比分析
简支组合箱梁自振频率对比见表1。其中:f1为本研究理论方法自振频率;f2为传统理论方法自振频率,其在本研究理论的基础上忽略了剪滞翘曲应力自平衡条件的影响;f3为Timoshenko 梁理论自振频率,其同时忽略了剪力滞效应和剪滞翘曲应力自平衡条件的影响;f4,f5,f6分别为欧拉梁理论、三维有限元和模型试验自振频率;f7为在本研究理论的基础上忽略了转动惯量影响的组合箱梁自振频率。
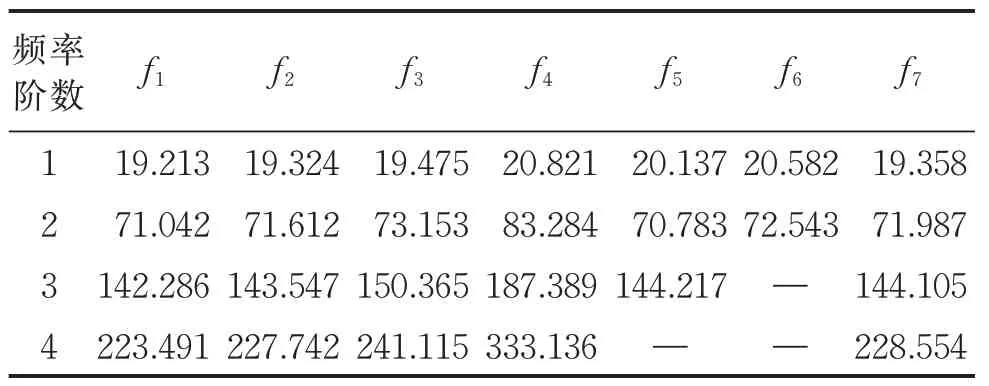
表1 简支组合箱梁自振频率对比Tab.1 Comparison of natural frequencies of simply supported composite box girderHz
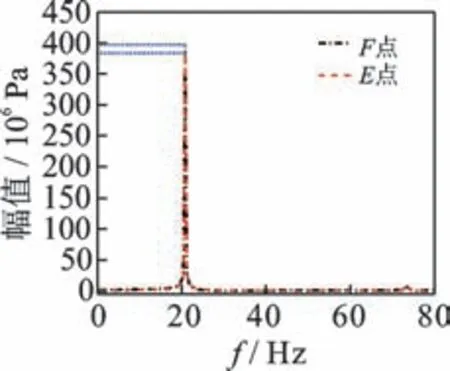
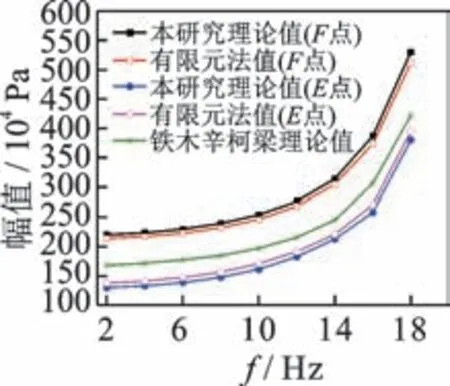
由表1 可以看出:本研究理论计算所得简支组合箱梁弯曲自振频率与有限元计算结果和实测值吻合良好,验证了该方法的准确性和有效性;根据欧拉梁理论所得组合箱梁自振频率与本研究理论和Timoshenko 梁理论相差较大,4 阶自振频率差值分别达到32.913%和27.623%,这主要是由于剪力滞效应和剪切变形降低了组合箱梁的竖向抗弯刚度,与剪力滞效应相比,剪切变形对结构抗弯刚度的影响更大;受剪力滞效应的影响,组合箱梁的各阶固有频率普遍减小,随着频率阶数的增加,剪力滞后效应的影响逐渐增大;剪滞翘曲应力自平衡和转动惯量对组合箱梁各阶自振频率的影响均小于5%。分析可知,本研究剪力滞理论所得结构自振频率值<传统理论值 采用3 种方法得到的简支组合箱梁前2 阶振型如表2 所示,表现出梁的竖向振动特性,理论振型和其他2 种方法得到的2 阶竖向振型吻合良好。 表2 简支组合箱梁前2 阶振型Tab.2 First two mode shapes of simply supported composite girder 为进一步分析简支组合箱梁的竖向动力反应特性,定义动剪力滞系数为本研究理论计算的动应力与Timoshenko 梁理论计算的动应力之比。在结构跨中作用一简谐集中力,该简谐力幅值为P0=19.6 kN。跨中截面上E点和F点的坐标位置如图2所示,运用有限元法计算组合梁E点和F点的动应力幅值,如图6 所示。 图6 有限元法计算组合梁E 点和F 点的动应力幅值Fig.6 Calculation of dynamic stress amplitude at E and F points of composite girder by finite element method 运用本研究计算方法求解组合箱梁动应力幅值流程如下:已知跨中作用简谐力幅值为P0,将不同简谐力频率ω代入式(29)后可得其8 个特征值;联立边界条件式(34)和式(35),得到8 个待定常数C1~C8的值;最后结合式(9)~(13),可得组合箱梁跨中截面两点(E,F)的动应力幅值对比见图7。 图7 组合梁E 点和F 点的动应力幅值对比Fig.7 Comparison of dynamic stress amplitudes at E and F points of composite girder 由图6,7 可以看出:在强迫振动分析中,剪力滞效应对组合箱梁翼板动应力幅值的影响较大,当简谐集中力作用频率相同时,F点的动应力幅值明显大于E点,即结构跨中横截面上各点的动应力幅值呈不均匀分布,其特点与文献[16]中关于该类结构的静力分析结果类似,因而动力分析时组合箱梁的平截面假定不再适用;同时,简谐集中力的频率值对组合箱梁的动剪力滞系数的影响普遍小于3.52%,分析时可忽略不计。 考虑结构宽跨比(2b1/L)对组合箱梁竖向弯曲振动特性的影响,保持组合箱梁其他尺寸不变,选取模型的宽度2b1为60 cm,其跨度从200~1 000 cm依次变化,研究宽跨比对简支组合箱梁固有频率比的影响,结果见图8。由图可以看出,简支组合箱梁的固有频率比随着宽跨比的增大而减小。当宽跨比小于0.15 时,固有频率比小于0.95,表明该条件下采用Timoshenko 梁理论计算结构基频可满足实际工程的精度要求;当宽跨比增大时,剪力滞效应对组合箱梁频率的影响逐渐增大;当宽跨比大于0.15 时,剪力滞效应对组合箱梁的第4 阶频率贡献值达到10.42%以上,所以在计算宽跨比较大的组合箱梁高阶自振频率时,剪力滞效应的影响不可忽略。 图8 宽跨比对简支组合箱梁固有频率比的影响Fig.8 Influence of width span ratio on natural frequency ratio of simply supported composite girder 宽跨比对简支组合箱梁动剪力滞系数的影响如图9 所示。由图9 可以看出:与传统剪滞理论相比,本研究理论所得E点和F点的动剪力滞系数与有限元解吻合更好;当宽跨比为0.3 时,F点的动剪力滞系数增大了9.4%,E点的则减小了8.7%,说明引入剪滞翘曲应力自平衡条件可提高组合箱梁翼板动应力幅值的计算精度;在强迫振动分析中,F点的动剪力滞系数随宽跨比的增大而增大,E点的随宽跨比的增大而减小,说明宽跨比越大时剪力滞效应对组合箱梁翼板动应力幅值的影响越大,剪滞翘曲应力自平衡的影响亦随之增大。 图9 宽跨比对简支组合箱梁动剪力滞系数的影响Fig.9 Influence of width span ratio on dynamic shear lag coefficient of simply supported composite girder 1)以能量变分法和Hamilton 原理为基础,提出一种能准确分析波形腹板钢箱组合梁弯曲振动特性的解析法,计算结果与ANSYS 有限元计算值和模型试验值吻合良好,且具有较高的计算精度。本研究计算方法编写Matlab 计算程序后操作方便且用时较短,避免了ANSYS 有限元模型求解的复杂性,因而具有一定的工程实用价值。 2)在强迫振动分析中,剪力滞效应对组合箱梁翼板动应力幅值的影响较大,在简谐集中力作用下,结构跨中横截面上各点的动应力幅值分布特点与其静力分析结果类似,而简谐集中力的频率值对组合箱梁的动剪力滞系数的影响普遍小于3.52%,分析时可忽略不计。 3)剪力滞效应对组合箱梁自振频率的影响随宽跨比的增大而变大,当宽跨比小于0.15 时,采用Timoshenko 梁理论计算结构自振频率可满足工程精度要求;当宽跨比大于0.15 时,剪力滞效应对组合箱梁的第4 阶频率贡献值达到10.42%以上。 4)虽然剪滞翘曲应力自平衡对组合箱梁各阶自振频率的贡献值较小,但本研究理论所得E点和F点的动剪力滞系数与有限元解吻合更好,说明引入剪滞翘曲应力自平衡条件可提高组合箱梁翼板动应力幅值的计算精度。剪力滞效应对组合箱梁翼板动应力幅值的影响随宽跨比的增大而变大,剪滞翘曲应力自平衡的影响亦随之增大。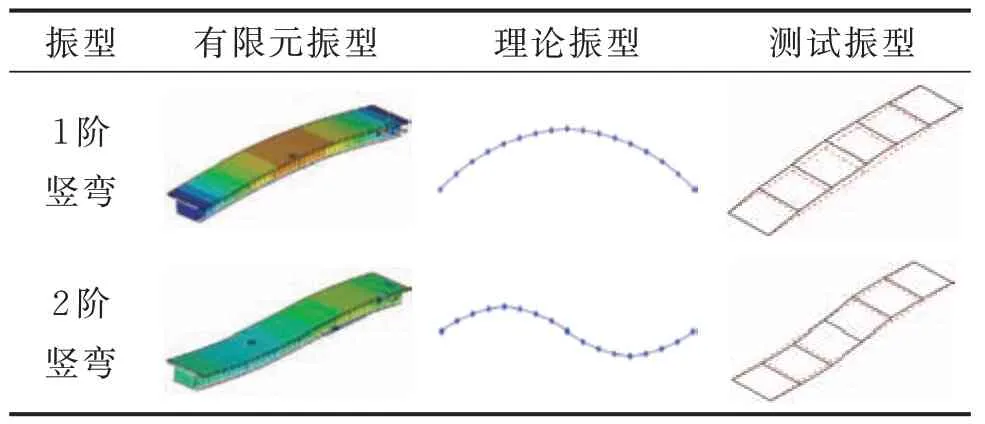


6 结论
