超声喷丸换能器的高电压阻抗匹配设计∗

施陆锴，芦小龙，李武琴，钱 丰，曹 达，李华峰

（南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

引言

超声喷丸成形技术是一种利用超声换能器驱动金属介质（撞针或弹丸）产生高频冲击作用于金属表面，实现钣件成形与校形的先进冷加工无模成形技术［1-2］。超声喷丸成形技术具有能量密度高、操作方式灵活、加工成本低和绿色无污染等特点，目前已经在飞行器、船舶及汽车等工业领域得到广泛使用。例如，法国SONATS 的STRESSVOYAGER 设备和德国KSA 的7 轴数控喷丸系统均在波音、空客等公司的诸多项目中发挥着重要作用，而国内相关的研制工作仍处于起步阶段［3-5］。作为超声喷丸成形系统的核心部件之一，超声喷丸换能器的工作特性直接决定了喷丸成形的效果。由于在低频超声领域内对换能器功率以及端面振幅的要求较高，夹心式构型的超声换能器获得了广泛应用［6］。这类结构能够承受较高的工作电压，避免压电陶瓷片在工作时发生应力破坏，金属端盖的良好传热性能为换能器的稳定工作提供了保障［7］。但是，不同的驱动电压和工作频率下超声换能器的阻抗特性并非稳定不变，为了获得最佳的工作特性，需要采用准确的匹配补偿方法提高其能量传输效率。

常见的匹配方式包括声学匹配和电学匹配［8］。声学匹配主要是通过添加匹配层材料以实现声阻抗的匹配或过渡［9］。文献［10-11］利用KLM 模型估算压电元件尺寸。Li 等［12］利用压电等效电路确定匹配层的间隔，训练神经网络模型以表征匹配层厚度和超声换能器性能之间的关系。面向大功率作动的超声换能器，如用于超声喷丸的则优先考虑电学匹配，以实现调谐、变阻及滤波的功能［13］。Lin 等［14］认为当换能器在其共振频率附近受到激励时，其输入阻抗表现为容性，应采用感性元件对容性阻抗进行补偿。Jiang 等［15］分析换能器串联电感匹配前后等效电路阻抗圆的位置，发现匹配后最佳振荡频率小于换能器机械共振频率，提出了最佳共振区匹配理论。Wang 等［16］将只包含1 个电容和电感的LC 匹配网络和超声换能器等效为数学模型，重新定义了由匹配元件带来的新谐振频率，使得负载阻抗和视在功率随负载的变化而保持恒定。尽管超声换能器匹配在理论计算和软件仿真方面取得了较多进展［14-18］，但参数的获取仍受限于阻抗分析仪等低压测试设备，而阻抗特性随电压的变化尚不明确，上述研究成果并不能直接应用于高电压驱动场合。

为研究高电压下超声换能器阻抗特性的变化，笔者采用功率放大器模拟高电压驱动，记录换能器两端的电信号参数并计算高电压工况下的阻抗特性，结果表明，高电压下换能器谐振频率会发生偏移。在偏移后的谐振频率附近选择工作频率并进行匹配，分析了加入匹配元件后负载电路的变化，研究了串联电感、并联电感对谐振频率、反谐振频率和有效机电耦合系数的影响。采用激光位移传感器观测匹配前后喷丸枪端部撞针的振幅变化，验证了匹配参数的正确性。该方法避免了传统低电压阻抗测量方法无法实现高电压阻抗精确匹配的问题，为进一步提高超声换能器的输出功率奠定了基础。

1 超声喷丸换能器及匹配方法

本研究试制的便携式超声喷丸成形系统如图1所示，包括撞针式的喷丸枪以及驱动电源，其核心构件为图2 所示的夹心式超声喷丸换能器。超声喷丸换能器在理想匹配工况下，能够作为阻性负载，将输入电能最大限度转化为超声振动，驱使冲击撞针产生高冲击载荷作用于金属材料表面，产生远大于材料屈服强度的冲击力，诱导材料内部重构应力，进而引发宏观的弯曲变形。

图1 超声喷丸成形系统Fig.1 Ultrasonic peen forming equipment

图2 夹心式超声喷丸换能器Fig.2 Sandwich-type ultrasonic peening transducer

夹心式超声喷丸换能器（以下称超声换能器）是一种将超声信号转化为机械振动的器件，其输出效能与节点设置、器件装配以及匹配电路参数密切相关。其中，匹配电路的好坏决定了换能器是否能够安全高效工作，而传统匹配参数的选择依赖阻抗分析仪等低电压测试设备，这类方法在高电压驱动下缺乏实用性。笔者提出的高电压电阻抗法，直接依据超声换能器在高电压下的阻抗虚部计算匹配电感，从而实现超声换能器的高电压精确匹配。

2 高压电阻抗匹配

2.1 试验方法

高电压驱动下超声换能器的谐振频率以及阻抗特性变化尚未明确，需先获取该工况下超声换能器的阻抗再进行匹配。笔者提出的高电压阻抗测试原理如图3 所示。采用功率放大器模拟超声换能器工作时的驱动电压，利用示波器获取高电压驱动下的电信号参数，其中超声换能器可等效为静态电容C0、动态电感L1、动态电容C1和动态电阻R1的串并联［6］，试验平台见图3（a）。功率放大器提供频率范围为17 kHz～21 kHz 的100 V 正弦交流信号，正负两端分别接至超声换能器的信号端和接地端，并在信号端前接入1 V/1 A 电流探针，示波器通道1 和通道2 显示实时电压和电流。试验过程中的电信号参数获取方式见图3（b），其中红色为电压波形，蓝色为电流波形，将示波器显示信号设置合适范围，将两路指针分别移至该路信号的峰值，读出电压峰值Umax（红色方框）、电流峰值Imax（蓝色方框）和两路信号之间的时间差ΔT（绿色方框）。利用时间差结合驱动频率，计算电压与电流信号之间的相位差。

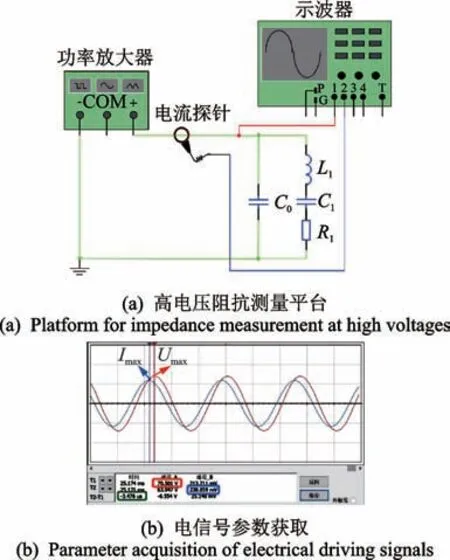
图3 高电压阻抗测试原理Fig.3 Principle of high-voltage impedance measurement

超声换能器的阻抗计算公式为

其中：ZT为超声换能器阻抗；φ为电压电流的相位差，即超声换能器的阻抗角；ΔT为两路指针的时间差；f为功率放大器输出的正弦信号频率，其范围为17 kHz～21 kHz；Re（ZT）为阻抗实部；Im（ZT）为阻抗虚部。

根据式（1）～（5）能够计算出在高电压下超声换能器的实际阻抗，通过调整功放频率，可以完成在指定频率范围内的电学特性曲线测试。将功率放大器的稳态输出电压调至峰峰值100 V，不同电压下超声换能器的电学特性变化如图4 所示。相较于阻抗分析仪（如PV80A 测试电压仅为3 V），在100 V 高电压下所测得的谐振频率fs1和反谐振频率fp1分别为18.62 kHz 和19.31 kHz，均略低于阻抗分析仪测得的谐振频率fs0（约18.75 kHz）和反谐振频率fp0（约19.36 kHz），这将导致在工作频率下选取的匹配参数产生差异。电感匹配方式能提高有效机电耦合系数［13］，因此选择略低于谐振频率且阻抗呈现容性的18.5 kHz 作为工作频率并进行后续匹配计算。图4（b）中100 V 下的幅频曲线（左轴阻抗模对数和右轴阻抗相位）并不规整，主要误差源于测量时的采样间隔。阻抗分析仪在谐振频率附近和非谐振频率区间的采样间隔分别为2.5 和25 Hz，而高电压阻抗法采样的间隔分别为10 和100 Hz。虽然采用更小的间隔必然使测得的阻抗更为精确，但也因此带来巨大的工作量，而对工作频率及匹配参数的选择并没有显著的提升。

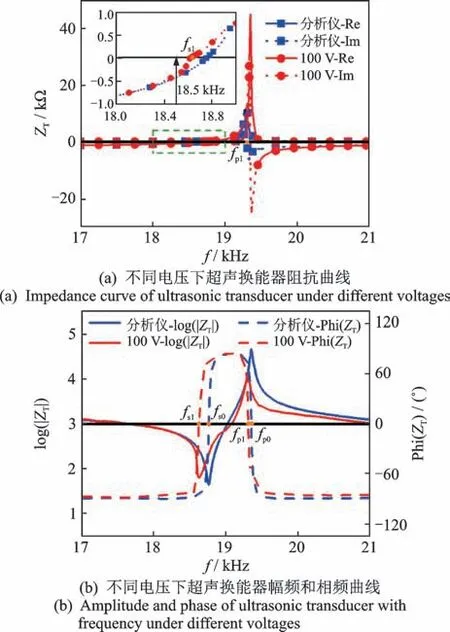
图4 不同电压下超声换能器的电学特性变化Fig.4 Changes of electrical characteristics of ultrasonic transducers under different voltages

2.2 并联电感匹配

超声换能器的阻抗表达形式通常等效为容性元件和阻性元件的串联，但为简化并联电感计算，需将其等效为容性器件和阻性器件的并联，超声换能器并联匹配原理如图5 所示。

图5 超声换能器并联匹配原理Fig.5 Parallel matching principle for UPF transducer

并联匹配电感计算公式为

其中：Zin1为加入并联电感后的负载电路总阻抗；Zpar为并联匹配电感的等效阻抗；Lpar为并联匹配电感。

根据图4 测得超声换能器18.5 kHz 处总阻抗为383 Ω，虚部为-379 Ω，代入式（7）计算得并联匹配电感的理论值为3.3 mH。考虑到实际使用的匹配电感元件的电感值与理论值存在一定的偏差，在理论值附近选择2.9 和3.7 mH 电感作为对比。接入不同匹配电感后以相同的高电压方式测量负载电路的电压和电流的峰值以及相位差，并联电感匹配的负载电路阻抗特性如图6 所示。

由图6（a）可知，引入并联电感对负载电路的反谐振频率影响较大。原阶次的反谐振频率fp1已移至更高的频率点，超出21 kHz；而上一阶次的反谐振频率fp2移至18.5 kHz 附近。由图6（b）可知，并联电感的加入未使得本阶次谐振频率fs1改变，但在低于fs1的地方出现上一阶次的反谐振频率fp2，这将导致工作频率附近阻抗特性的突变，严重影响换能器的工作稳定性。在并联3.3 mH 电感情况下，工作频率18.5 kHz对应的负载电路阻抗虚部值为-1 731 Ω，高于匹配前的阻抗虚部值，因此并联电感匹配由于干扰阶次的引入未能实现理想匹配状态。虽然并联电感未能使工作频率点呈现纯阻性，但在高于fs1处，3种感值的并联匹配结果均使得超声换能器的阻抗虚部变小，这对于抵消喷丸过程中机械负载变化而引起的电学等效阻抗波动具有一定的积极效果。

2.3 串联电感匹配

串联匹配的电感值直接采用阻抗虚部进行计算，串联电感后的负载电路等效模型如图7 所示。

图7 串联电感负载电路等效模型Fig.7 Serial matching circuit equivalent model with an inductance load

串联匹配电感计算公式为

其中：Zin2为加入串联电感后的负载电路总阻抗；Zser为串联匹配电感的等效阻抗；Lser为串联匹配电感。

由超声换能器18.5 kHz 处的阻抗以及式（9）即可计算得到理想的串联匹配电感值为3.2 mH。与并联匹配试验研究相同，采取理论电感值附近不同的电感设置，测试串联匹配后的超声换能器阻抗特性。在相同的输入电压幅值以及测试频率区间下，测得的串联电感匹配的负载电路阻抗特性如图8所示。

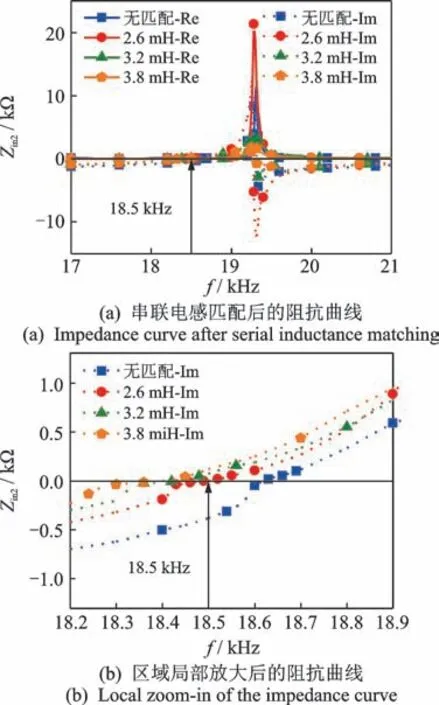
图8 串联电感匹配的负载电路阻抗特性Fig.8 Impedance characteristics of load circuit with a serial inductance matching

由图8（a）可知，引入串联匹配电感对超声换能器原有阶次的反谐振频率fp1几乎没有影响，均维持在19.3 kHz 左右；原有阶次的谐振频率fs1对应的电学阻抗随着串联电感值的升高而降低。由图8（b）可知，串联电感使得超声换能器的谐振频率发生了漂移。当串联电感值为2.6 mH 时，谐振频率点移至18.5 kHz，与设定的超声换能器工作频率点相重合，实现了预期的匹配效果。此时的超声换能器等效电路呈现纯阻性，输入电能全部转化为机械能输出，有功功率达到最大值。

超声换能器的有效机电耦合系数计算公式［6］为

其中：keff为有效机电耦合系数。

由式（10）可得，无论是并联电感升高反谐振频率，还是串联电感降低谐振频率，均可使有效机电耦合系数增大。

电学匹配理论分析和试验结果均表明，高电压下的超声换能器匹配具有一定的复杂性，不能直接采用阻抗分析仪测量的结果进行精确匹配。相较于并联电感匹配，串联电感匹配针对超声换能器指定的工作频率点具有更好的匹配效果。串并联不同电路元件的电学匹配方式非常丰富，各自展现出不同的优缺点［19-21］。

3 喷丸枪撞针振幅试验

超声换能器端部的超声振动，通过撞针的运动将能量传递至目标工件，在高速冲击的情况下实现工件的塑性变形。因此，撞针运动的强度直接反映了超声换能器的功率输出能力，通过观测喷丸撞针的位移变化即可判定超声换能器的输出性能。图9所示的喷丸撞针运动试验平台，采用KEYENCE LK-H150 型激光位移传感器单点测量撞针端部的纵向位移，采样周期设为0.2 ms，此时精度为0.01 μm，量程为0～80 mm，以覆盖撞针运动全过程。驱动电源采用笔者团队自行研制的超声喷丸成形驱动电路，频率范围为15～25 kHz，在不接匹配电路的情况下能产生峰峰值为340 V 的方波驱动信号。将超声喷丸枪倒立放置，喷丸枪头部仅安装少量撞针，以减少喷丸过程中的相互干扰。笔记本电脑用于实时记录激光位移传感器测得的撞针瞬态运动。

图9 喷丸撞针运动试验平台Fig.9 Test platform for movement detection of impact pins

通过调频旋钮设置驱动板输出频率为18.5 kHz，喷丸撞针动态运动试验结果见图10。由图10（a）可知，匹配前的撞针运动位移幅值约为2.7 mm，且位移幅值在不同的运动周期呈现一定的波动性。由图10（b）可知，匹配后的喷丸撞针瞬态运动中，位移峰值能够达到4.9 mm，约为匹配前的1.8 倍。对撞针位移作频域分析并以300 Hz 幅值为基准表征0～300 Hz 区间内信号的强度，结果表明匹配前后冲击运动的频率约为130 Hz。由此可见，高电压阻抗匹配设计能够提高超声喷丸成形系统的功率输出能力，有效提升喷丸撞针的冲击强度。通过理论计算工作频率点对应的串联匹配电感值，再经过微幅调整，即可实现超声换能器等效电路的纯阻性负载特性，有效提高功率输出。相较于利用阻抗分析仪测得的超声换能器夹持电容、动态电阻等参数计算法，高电压阻抗匹配法更为准确直接，在提升超声换能器的驱动能力方面得到了充分验证。

图10 喷丸撞针动态运动试验结果Fig.10 Measured dynamic movement of impact pins

4 结论

1）在高电压驱动工况下，超声换能器的谐振频率和电学阻抗变化显著，阻抗分析仪所测得的频率和阻抗在高电压驱动下并不适用。

2）针对超声换能器，并联匹配方式由于上一阶干扰模态反谐振点的并入，使得工作频率附近的换能器等效电路呈现突变，无法实现纯阻性的匹配需求。串联电感方式能够将谐振频率点调整至与工作频率相重合，串联2.6 mH 电感使得负载电路阻抗虚部接近于0，能够满足纯阻性的匹配需求，有效提升了有功功率。

3）采用高电压串联匹配设计，能够在使用相同超声换能器的情况下，将喷丸撞针的冲击运动幅值提升至匹配前的1.8 倍，表明高电压阻抗匹配设计有效提高了超声换能器的输出特性，对进一步研制大功率高性能超声喷丸成形系统打下了基础。