基于声纹的GIS 断路器机械故障诊断∗

李 可，姚忠远，王 枭，顾杰斐，宿 磊，薛志钢

（1.江南大学江苏省食品先进制造装备技术重点实验室 无锡，214122）（2.上海睿深电子科技有限公司 上海，201108）（3.江苏省特种设备安全检验监督研究院无锡分院 无锡，214071）

引言

气体绝缘开关设备具有可靠性高、维护方便等优点，被广泛应用于高压电力系统。断路器作为GIS 的关键组成部分，对电力系统起到了保护和控制的作用［1］。据统计，断路器机械故障是导致GIS故障主要原因［2］。通过有效方法准确诊断识别断路器的机械故障，对保障电力的安全稳定输送具有重大意义。

工程实际中一般通过接触式传感器采集断路器的机械振动信号，然后使用各种算法对信号进行分析处理，以实现断路器机械故障的诊断。Huang等［3］提出了一种基于经验模态分解（empirical mode decomposition，简称EMD）和支持向量机（support vector machine，简称SVM）的高压断路器故障诊断方法，利用遗传算法优化了SVM 的超参数，诊断精度优于传统分类方法。Zhang 等［4］利用集成经验模态分解将原始信号分解为多个本征模态函数（intrinsic mode functions，简称IMF），提取IMF 的能量熵作为SVM 的输入，有效识别了断路器的故障模式。Wan 等［5］提出了一种基于时序参数和模糊C 均值聚类（fuzzy C-means clustering，简称FCM）的故障诊断方法，利用双阈值法提取振动事件的发生时间和结束时间作为特征向量，采用FCM 计算特征向量的聚类中心，实现了断路器故障类型的准确分类。

断路器在合分闸时产生的机械振动和声音信号包含了大量设备状态信息，而振动传感器需要安装在GIS 设备内部，造成机械振动信号的采集较为困难。此外，较小的位置偏移会引起测量结果产生较大变化，所以基于机械振动的故障诊断方法对加速度传感器布点位置的要求也比较高［6］。基于声信号的检测方法具有非接触式、带电检测的优点，适用于断路器的机械故障诊断。陈朋永等［7］利用EMD 提取声波信号等时间分段的能量熵作为特征向量，结合SVM 诊断出断路器的不同状态，有效解决了小样本下断路器故障诊断的问题。杨元威等［8］提出一种基于声音信号的高压断路器机械故障识别方法，通过K-S 检验标记样本幅值差异明显的区间，提取区间内的少量信号特征识别出故障信号。

目前，声学诊断方法大多应用于旋转机械的故障诊断，基于声信号的GIS 断路器机械故障诊断方法的研究较少，且单一通道采集的信号数据极易受环境噪声的影响。笔者提出了一种基于声纹的GIS断路器机械故障诊断方法。首先，利用多通道声阵列采集信号，采用ICA 算法实现原始信号的盲源分离；其次，选取源信号中模糊熵最小的分量作为特征信号，并提取特征信号的MFE 生成断路器的声纹；最后，采用ELM 算法进行状态识别。实验结果表明，所提出的方法可以有效识别断路器机械故障。

1 断路器故障诊断方法

1.1 独立成分分析

ICA 是一种将复杂混合信号解耦的盲源分离技术，其仅依靠观测信号来恢复源信号［9］。将多通道声传感器阵列采集到的原始观测信号记为X=（x1，x2，…，xn）T，源信号记为S=（s1，s2，…，sn）T，则ICA 模型可表示为

其中：A为混合矩阵。

通过解混矩阵W可得到对源信号S的估计Y=（y1，y2，…，yn）T，即

选取合适的解混矩阵W可实现独立分量的分离。基于负熵的最大非高斯估计方法是一种鲁棒性强、收敛速度快的ICA 算法。该方法通过度量分离结果的非高斯性来评估分量间的相互独立性，其基本步骤［10］如下：

1）对原始信号X进行中心化和白化处理；

2）记l为待分离信号通道数，初始化迭代次数k=1；

3）随机选择初始向量wk，wk为解混矩阵W的一个向量；

5）对wk进行正交化和归一化处理；

6）判断wk的收敛性，若不收敛返回步骤4，否则进行下一步；

7）令k=k+1，若k≤l，返回步骤3，否则算法结束。

1.2 模糊熵与多尺度模糊熵

模糊熵是一种量化时间序列复杂度的方法，序列的复杂度越大则熵值越大，其具体计算过程参考文献［12］。多尺度模糊熵是衡量时间序列在不同尺度下的模糊熵，具有抗噪和抗干扰的优点，能够有效表征机械设备的故障特征［13］。MFE 的主要计算过程如下。

1）粗粒化时间序列y（i），1≤j≤N，将y（i）分成τ段，每段长度为N∕τ，即

其中：τ为时间尺度因子。

2）给定嵌入维度m、相似容限r和模糊函数梯度n，对每段粗粒化序列计算其模糊熵（FuzzyEn）

本研究先选取源信号中模糊熵最小的分量作为特征信号，然后计算特征信号的MFE 来生成断路器的声纹特征。

1.3 极限学习机

极限学习机是一种单隐层的前馈神经网络算法，输入层与隐藏层的节点参数随机生成，且无须调整，具有训练速度快、识别精度高的优势。假设样本（V，T）=｛（vi，ti）｝（i=1，2，…，N），其中vi为输入样本，ti为样本标签，N为样本数，则ELM 的输出为

其中：L为隐藏层节点数；βi为隐藏层第i个节点和输出层的连接权重；P（x）为特征映射函数，通常采用Sigmoid 函数；ai为输入层和隐藏层第i个节点的连接权重；bi为隐藏层第i个节点的偏差。

因此，网络的输出矩阵为

其中：H为隐藏层输出矩阵。

输出权重β可通过采用最小二乘法求解式（6）获得［14］，即

其中：H†为H的广义逆矩阵。

1.4 诊断流程

综上所述，笔者提出的基于ICA-MFE-ELM 算法的断路器机械故障诊断流程如下：

1）采用ICA 方法将断路器声信号进行盲源分离，得到多维源信号yi（i=1，2，…，n）；

2）计算所有yi的模糊熵，选择其中熵最小的信号ym作为特征信号；

3）计算特征信号ym的MFE 作为断路器的声纹特征；

4）利用ELM 识别断路器的机械故障。

2 实验验证与结果分析

2.1 实验数据采集

实验现场及设备如图1 所示，实验使用某型号110 kV 的GIS 设备。当GIS 断路器开断电路时，触头间会产生电弧，电弧高温容易造成如图2 所示的触头烧蚀，导致断路器发生开关拒动等机械故障［15］。为了采集故障信息，实验设计了触头正常和触头烧蚀2 种工况。

图1 实验现场及设备Fig.1 Experimental site and equipment

图2 触头烧蚀Fig.2 Contact ablation

数据采集装置为睿深电子科技的声学成像设备soundCAM，该设备上搭载了由64 个声学传感器组成的声阵列，传感器的频响范围为20 Hz～24 kHz，最大可测声压级为120 dB。待测断路器与声阵列平行放置，测试距离为2 m。实验时对断路器声信号进行同步采样，采样率为48 kHz。

实验采集了断路器从合闸前到分闸后共16 s 的声音数据。为减少信号处理时间，截取了合分闸动作信号附近0.5 s 的数据作为原始信号。图3 为原始声音信号的波形图，由图可见，2 种状态下的声信号包含了大量的背景噪声，很难直接进行区分。

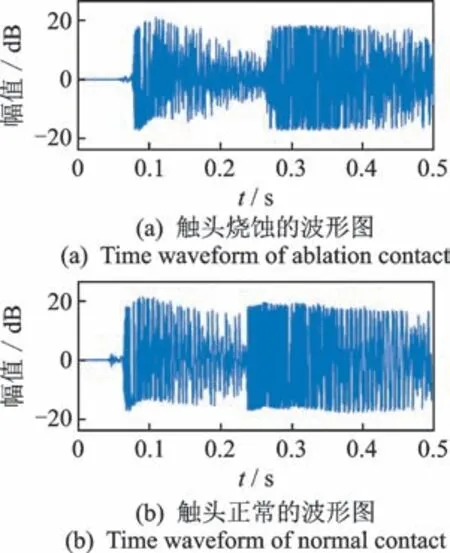
图3 原始声音信号的波形图Fig.3 Time waveform of original sound signals

2.2 特征信号选取

首先，采用ICA 算法对原始信号进行处理，输入为32 通道的原始声信号，输出为32 组源信号；其次，选取源信号中模糊熵最小的分量作为特征信号。按照模糊熵的定义，计算前需要确定嵌入维度m、模糊函数梯度n和相似容差r等3 个参数。根据本研究声音序列的特点，参考文献［16］，信号长度N=10m～30m。本研究信号长度为24 414，故综合考虑选取m=4，n=2 或3，r=0.15SD～0.25SD（SD 为信号数据的标准差）。由于选取较小参数可获得数据中更多的细节信息，因此本研究取n=2，r=0.15SD。图4 为所选取特征信号的波形图。

图4 特征信号的波形图Fig.4 Time waveform of characteristic signals

随机选取触头烧蚀和触头正常的声信号样本各30 组，用以比较ICA 处理前后信号的熵值变化。原始信号和特征信号的熵值分别如图5，6 所示。对比图5，6 可知，无法根据原始信号的熵值辨别断路器的2 类状态，而经过ICA 处理后不同状态的特征信号熵值区分度明显。然而，因为单一尺度的模糊熵易受噪声干扰，难以全面反映断路器信号的本质特征，故有必要从多尺度上提取其声纹特征。

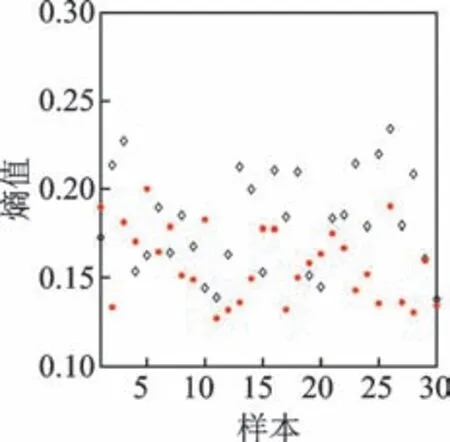
图5 原始信号的熵值Fig.5 Entropy values of original signals

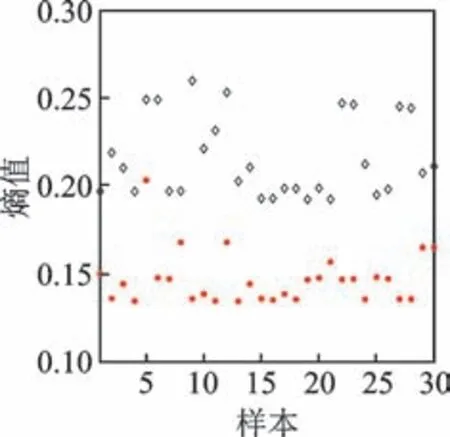
图6 特征信号的熵值Fig.6 Entropy values of characteristic signals

2.3 声纹特征提取

利用MFE 算法提取断路器的声纹特征，选取了10 种不同的尺度因子τ，计算特征信号的模糊熵值。不同状态的多尺度模糊熵如图7 所示。由图可知：触头烧蚀的熵值随着尺度增加而增加，表明该序列比较复杂，在多个尺度上包含重要的信息，随后趋于平稳；触头正常的熵值先增加，当τ为6 时，熵值逐渐减小，表明触头正常的特征信号熵值在大尺度下不稳定。因此，取尺度因子τ分别为1，2，3，4 和5，提取特征信号的多尺度模糊熵作为断路器的声纹特征。实验共采集了440 组数据，其中包括触头烧蚀220 组，触头正常220 组。触头烧蚀和正常的声纹分别如表1，2 所示。

表1 触头烧蚀的声纹Tab.1 Voiceprint of contact ablation

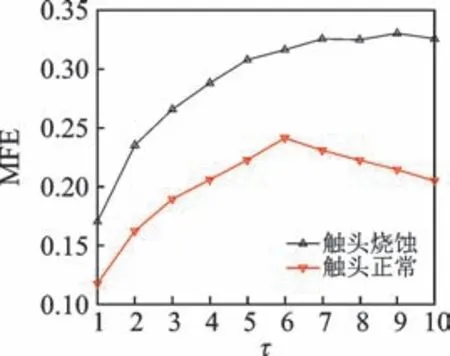
图7 不同状态的多尺度模糊熵Fig.7 MFE of different states

随机挑选了2 种状态各4 组特征信号的声纹特征，不同状态的声纹比较如图8 所示。由图可以看出，随着尺度因子的变化，不同状态的MFE 差异明显，利用多尺度模糊熵方法能够有效提取断路器的声纹特征。

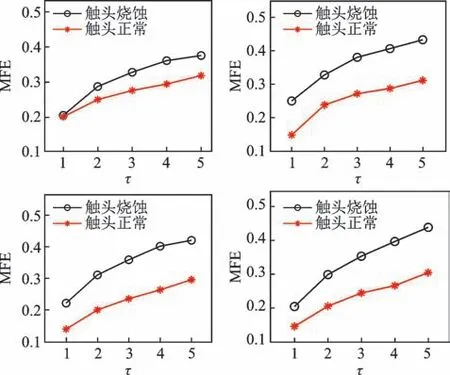
图8 不同状态的声纹比较Fig.8 Comparison of voiceprints in different states

2.4 故障识别

采用ELM 算法识别断路器触头的故障类型，每类状态各220 个样本。设定训练集、验证集和测试集的比例为3∶1∶1。当隐藏层节点数L=10 时，训练正确率可达99%以上，测试正确率达到97.6%。

为验证所提方法的有效性，将本研究算法与其他基于声音信号的故障诊断方法进行对比，对比算法如下。

1）利用奇异谱分析（singular spectrum analysis，简称SSA）对声信号进行分解重构，去除噪声分量，提取重构信号的时域和频域特征，结合SVM 实现故障分类［17］。SVM 采用高斯核函数，通过交叉验证确定最优的惩罚系数c=2.3 和核函数宽度g=24.25。

3）从声音信号中提取梅尔频率倒谱系数（Mel-frequency cepstrum coefficients，简称MFCC）作为特征向量，利用梯度提升决策树（gradient boost decision tree，简称GBDT）进行故障分类［19］。树的深度为3、个数为50。

4）将本研究所提方法中MFE 替换为多尺度排列熵（multi-scale permutation entropy，简称MPE），不同算法的诊断正确率如表3 所示。由表可知，所提出方法（ICA-MFE-ELM）的故诊断正确率明显高于其他算法。MFE 通过引入模糊函数使得熵值连续平滑变化，当信号存在波动或基线漂移时，模糊熵具有一定的抗干扰能力。由于实验信号属于非平稳信号，因此模糊熵较排列熵能更好地提取信号的特征。

表3 不同算法的诊断正确率Tab.3 Diagnostic accuracy of different algorithms

3 结束语

提出了一种基于声纹的GIS 断路器机械故障诊断方法，能够有效减少噪声干扰并且提取故障特征。该方法采用ICA 分析声阵列采集的GIS 断路器信号获得多维源信号，根据模糊熵原理选取特征信号，并计算其MFE 作为声纹特征，最后利用ELM实现故障识别。实验结果表明，本研究所提方法的故障诊断正确率在97%以上，较其他方法有明显提高。