基于影像及小波变换的桥梁损伤识别

郑佳艳, 李衡, 刘海京, 刘琰, 罗仁伟, 陈海林

(1.重庆交通大学土木工程学院, 重庆 400074; 2.招商局重庆交通科研设计研究院有限公司, 重庆 400076)

桥梁是人们生活中最常见的工程结构之一,其结构在风、地震、交通等随机荷载作用下容易发生振动,关键结构构件造成损伤(疲劳和开裂),结构健康监测(structure health monitor)或无损损伤评估(no damage evaluate)对保障结构安全、提高经济效益有重要的理论意义和工程应用价值。损伤检测和评估通常包括判断损伤是否存在、确定损伤位置、估计损伤严重程度、评估剩余性能等4个步骤。

近几十年以来,基于振动的结构健康监测技术在土木工程领域中一直是人们的研究热点,也是应用最广泛的无损检测技术之一,它基于结构动态特征参数的变化识别结构损伤,如固有频率、振型、模态应变能和频率响应函数[1-2]。固有频率[3]是最广泛使用的基于振动的损伤指标之一,但识别损伤位置非常困难。结构局部发生损伤导致的局部刚度降低会影响损伤区域振型的连续性和光滑性,通过分析振型及其高阶导数可用于结构损伤识别[4]。在此基础上,将振型或振型曲率与信号处理技术相结合,如小波变换、神经网络和高斯过程分类,可显著提高损伤检测的准确性和精度。小波变换(wavelet transform,WT)作为一种高效的信号处理工具可对信号进行局部分析,且对信号微小突变非常灵敏,在结构与机械工程损伤识别和定位的应用已经成为健康监测的热点研究方向。Shi等[5]提出了一种二维方向连续小波变换的板结构线型损伤检测算法,通过人工诱导缺口铝合金夹板的模态试验验证了该算法的有效性和实用性。Wu等[6]利用空间小波变换对梁结构在静力位移下的裂纹检测进行了实验研究,结果表明小波变换可以识别或放大这种小扰动,有效定位裂纹位置。Solis等[7]提出了一种新的小波分析梁损伤检测方法,通过分析振型变化定位损伤。Zhao等[8]基于简支钢筋混凝土梁有限元模型中提取的结构模态形状,利用不同类型小波进行了损伤识别。Katunin等[9]提出一种基于结构剪切测量结果的模态旋转场差异,并采用基于二维连续小波变换算法进行后处理的损伤识别方法。结果表明,该方法能够提高损伤的敏感性,能够有效地识别较小程度的损伤。Cui等[10]提出一种利用空间分布小波熵方法进行呼吸裂缝定位的新方法,在实验室中,应用该方法对带有预定义呼吸裂纹的光束振动响应进行了分析,进一步证明该方法的可行性。王盟等[11]将结构瞬时振型差进行小尺度小波变换,利用小波系数实部发生极大值时刻及发生位置识别结构损伤时间和损伤位置并用极大值大小来判定损伤程度,最后用一个悬臂梁和斜拉桥的数值算例验证了该方法。Sun等[12]研究了使用小波变换分析模态形状,并从小波系数中提取损伤指标的方法。此外,为了进行比较,还提取了其他两个损伤指标,即模态形状曲率和多项式拟合差,研究结果表明,小波分析能够有效地抑制测量噪声的影响,并精确地检测损伤的位置和大小。孙禹晗等[13]采用旋转悬臂梁模型模拟旋翼直升机桨叶结构,针对位移模态,基于小波变换的奇异性分析特性,研究了一种通过小波系数辅助损伤识别的方法。计算结果表明,在旋转结构中,位移模态结合小波变换的奇异性分析能够实现较为准确的损伤识别效果。方有亮等[14]利用小波包样本熵原理,研究了钢框架结构损伤定位识别方法。通过分析框架结构受冲击载荷时的动力响应,使用小波包分解对加速度信号进行处理,并创建小波包样本熵的损伤指标,该指标可使用单一传感器实现理想的识别效果,并具有适用性和鲁棒性。

但上述文献均是通过传统测量方式获取结构动态响应,如通过加速度计或应变传感器测量结构的动力响应,进而达到评估结构的安全状况或检测损伤的目的。

在预测结构的非线性行为方面,相比于结构的加速度或速度响应,位移本身包含了更多关于动力行为的信息。常用的位移测量方法分为接触式和非接触式两类,接触式位移响应检测方法主要包括线性可变差动变压器百分表,拉绳式位移传感器,线性可变差压传感器,磁致伸缩位移传感器,液位计等[15-16];非接触式位移测量有全球定位系统、激光多普勒仪、全站仪等。但上述用于测量结构位移的传感器在实际应用中存在局限性,这种传感器不仅安装烦琐、耗时、价格昂贵,还存在安装可达性差、使用寿命以及后期维护困难等缺点[17]。

随着科技和数字图像处理技术的发展,基于计算机视觉的结构位移监测方法也不断涌现出来,并在实际工程中得到广泛运用;基于视觉的位移传感器系统作为一种新兴的非接触式测量方法,与其他常用的接触式位移传感器相比,视觉传感器具有远距离、非接触、高精度、省时省力、多点监测等诸多优点,因此受到越来越多的科研和工程人员的关注。Cha等[18]实现了基于运动放大技术的相位光流算法用于结构位移测量,这种非接触式位移测量方法不需要密集的仪器,不会增加任何可能导致测量偏差的附加质量,且较传统方法可以测量更多的信号。郑佳艳等[19]提出了一种基于欧拉影像放大技术和边缘灰度均值差的非接触式测量方法,通过标定即可获取目标结构时域中的实际位移幅值。刘辉等[20]提出多视域下基于机器视觉的索力测试新方法,解决现有非接触视觉测量存在的测试视场不足和应用场景复杂多变的问题,该方法可以协调统一测试精度与视域范围之间的矛盾。郑晓昱等[21]针对目前人工测量存在的缺点,提出了一种基于激光点标定的视觉测量方法。该方法通过计算实际距离和图像上距离之间的比例来计算每个像素点的实际尺寸,从而得到门窗洞的实际尺寸。具体步骤包括:使用两个激光点标定距离,计算像素点对应的实际尺寸,使用图像处理算法测量门窗洞的图像尺寸,并计算其实际尺寸。Feng等[22]通过简支梁结构振动测试,结果表明视觉传感器对密集全场位移测量具有很高的精度,验证了视觉传感器的远程、实时、多点测量能力。叶肖伟等[23]提出了一种基于数字图像处理技术测量结构位移的方法,并介绍了基于模板匹配算法测量结构位移的计算过程,并对该系统分别进行实验室和现场标定试验来验证该系统用于结构位移测量的可行性以及测量精度的可靠性。Dong等[24]将基于机器视觉的传感技术与数字图像处理算法相结合,提出了结构动态位移的多点同步测量方法。利用实测多点动态位移,采用快速傅里叶变换(fast Fourier transformation,FFT)对结构模态参数进行辨识。在工程中,通常需要对结构进行振动测试来获得一些重要信息,如固有频率、振型等,利用这些数据不仅可以为结构设计提供有效的依据,另外还可用于分析地震作用下结构的反应。图像技术能够方便、快捷、直观准确地获取结构的动力响应及模态参数,这是其他方法所不能比拟的。但目前基于视觉进行结构动力响应监测与模态参数识别并应用到损伤识别中的研究较少。

综上所述,桥梁损伤识别中主要存在的问题是传统传感器在实际应用中存在一定的局限性,其自身附加质量会对结构的振动以及模态产生一定的影响,且传感器的布设总数决定振型的空间分辨率,对于基于振型的小波变换的损伤识别,该方法以振型作为输入信号,通过小波的奇异性检测能力识别损伤,所以振型的准确与否直接关系到损伤识别的结果,由此可能导致对结构的损伤定位不准确。为解决传统传感器测点布设不便、数量少以及自身重量对获取振动响应信号和模态参数的影响,提高损伤位置识别的精度及准确性,充分利用视觉传感器多点以及非接触监测的优点,现开发一种基于数字图像的结构响应测量与小波变换相结合的新型损伤检测技术。以悬臂梁为研究对象,通过数值模拟和模型实验予以验证,采用一种经济的基于数字图像的技术来获得悬臂梁的动态位移响应以及模态参数,通过室内悬臂梁结构实验来验证位移响应的有效性,通过FFT变换提取结构模态参数,与数值模拟结果吻合度高。最后,基于结构振型分析通过小波分析识别损伤的发生及位置。

1 基本理论

1.1 模板匹配的原理

模板匹配算法是一种广泛应用的模式识别方法,它归属于统计识别方法的范畴,通过先验信息选择包含目标点或者目标特征区域的图像子集作为模板,同时确定模版在原始图像中对应锚点的位置。将选择的模板与序列图像中对应的子集进行比对,并为像素单位从左至右、从上至下逐列逐行移动,每移动一个像素点以获得模板图像子集与序列图像重叠部分(目标子集)的像素灰度值进行相关运算。当相关运算系数取极值时认为匹配,表示模板图像与序列图像的子集达到最佳匹配,最佳匹配的位置即为目标点在序列图像中的位置。

如图1所示,以几何尺寸为W×H(单位pixel)的原始图像G左上角顶点为坐标原点建立直角坐标系,从原始图像中选取包含预设尺寸为m×n的目标模板子图像,模板左上角顶点(简称锚点)位于原始图像坐标内位置(i0,j0),则在位置(i0,j0)处的相关系数R(i0,j0)可以表示为

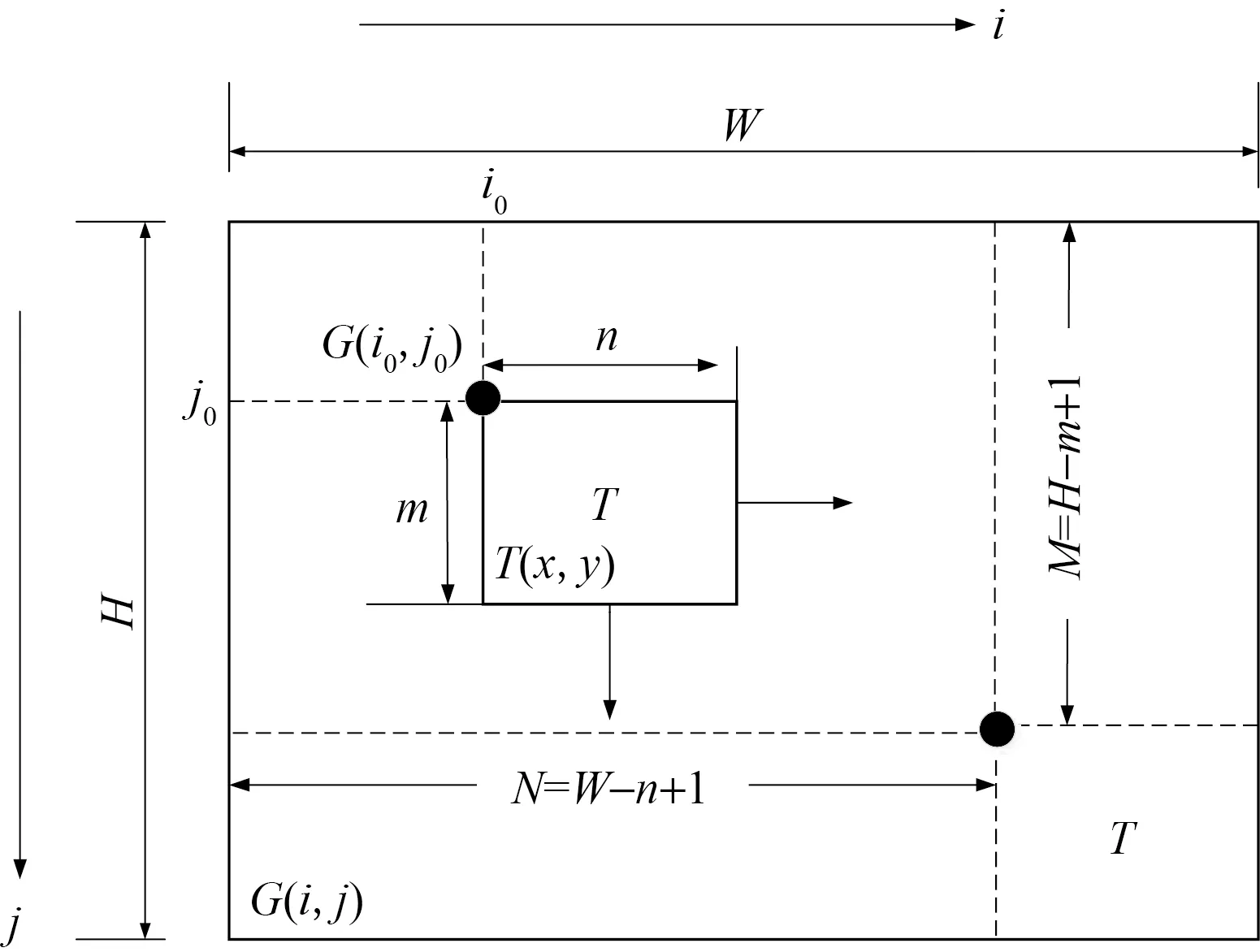
图1 模板匹配相关匹配过程示意图Fig.1 Schematic diagram of correlation matching process in template matching

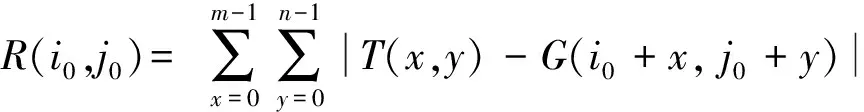
(1)

式(1)中:x=0,1,…,m-1;y=0,1,…,n-1;i0=0,1,…,M;j0=0,1,…,N。

相关匹配过程是将搜索模板T叠放在被搜索图G上遍历,模板覆盖被搜索图的区域称为子图G(i0,j0),(i0,j0)为子图锚点在被搜索图G上的坐标。模板T逐像素遍历并计算模板T与子图G(i0,j0)的相关系数,模板T在被搜索图像G的移动范围为M=H-m+1,N=W-n+1,当模板T完全遍历搜索图像G并计算相关系数,最终得到一个大小为(H-m+1)×(W-n+1)的相关系数矩阵,相关系数矩阵中极小值的位置即为搜索图像G与模板T匹配的最佳位置,即寻找的目标位置。

1.2 小波变换的基本概念

小波变换是一种积分变换,它是将一原始小波(称母小波,也称基本小波)进行缩放、变换,以生成后续小波(称子小波)的过程。

设ψ(x)∈L2(R)为小波母函数,其中,L2(R)为平方可积的实数空间和能量有限的信号空间,并满足容许性条件为

(2)

式(2)中:ψ(ω)为小波母函数ψ(t)的傅里叶变换。将基本小波ψ(t)经过伸缩和平移后可得

(3)

式(3)中:a为尺度参数,是反映某一具体基函数尺度大小(伸缩情况)的变量;b为平移参数,是反映其在x轴上平移大小的变量。

对任意信号f(x),其连续小波变换可以表示为

(4)

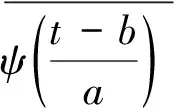
将小波变换的参数a、b进行离散化,并采用特殊的形式,即将尺度参数a按二进的方式离散化aj=2j,得到二进小波和二进小波变换,然后再将时间中心参数b按二进整数倍数的方式离散化,即bj=k2j,最后得其离散小波变换可以表示为

(5)

信号中的奇异点和不规则的变异成分往往含有大量信息,这是信号的重要特征之一。由于小波变换具有多分辨率时频分析特性,因此将小波变换用来检测信号奇异值的位置是非常有效的,如损伤或不连续性,因此可以采用小波分析辅助模态参数进行损伤识别。为放大损伤前后变化的奇异性,提高损伤识别的敏感程度,以小波系数平方差作为损伤指标,具体表示为

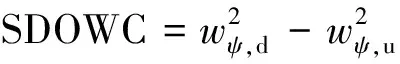
(6)

式(6)中:SDOWC为小波系数平方差;wψ,d为损伤后的小波系数;wψ,u为损伤前的小波系数。

2 悬臂竖梁数值模拟及验算

2.1 悬臂竖梁的数值模拟

为了验证模态参数小波变换方法用于损伤识别的可行性,采用一悬臂竖梁进行数值模拟,如图2所示,其尺寸和材料参数分别为:长L=1 000 mm、宽B=40 mm、厚H=1.7 mm、密度ρ=7.85×10-9kg/mm3、弹性模量E=200 GPa、泊松比μ=0.29。通过单元刚度折减来模拟结构的非线性损伤,有利于确定损伤程度大小,损伤程度用S表示。单元为D×B×H(50 mm×40 mm×1.7 mm,D为单元长度)的长方体减小弹性模量E的值模拟单元刚度损失。如图3所示,共设置D1～D4的4种损伤工况,其中9号单元单损伤的程度有10%、20%、40% 3种工况,多损伤工况是5号单元和16号单元两处位置,且损伤程度均为20%。具体损伤工况如表1所示。

表1 悬臂梁的损伤工况

图2 悬臂梁模型示意图Fig.2 Schematic diagram of cantilever beam model

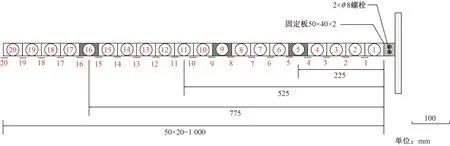
图3 悬臂梁单元划分Fig.3 Elements of cantilever beam

2.2 固有频率及验算悬臂梁模型

提取悬臂梁的前三阶频率数值模拟结果,在无损伤工况下,利用振动理论计算得到的理论值与模拟值如表2所示。前三阶固有频率的理论值与数值模拟结果的相对误差分别为一阶0.396%、二阶0.349%、三阶0.349%。由表2可知,两种方法得到的结构固有频率吻合度高,表明建立的有限元模型的正确性。悬臂梁在单损伤和多损伤工况下的固有频率如表3所示。

表2 悬臂梁无损时的固有频率对比

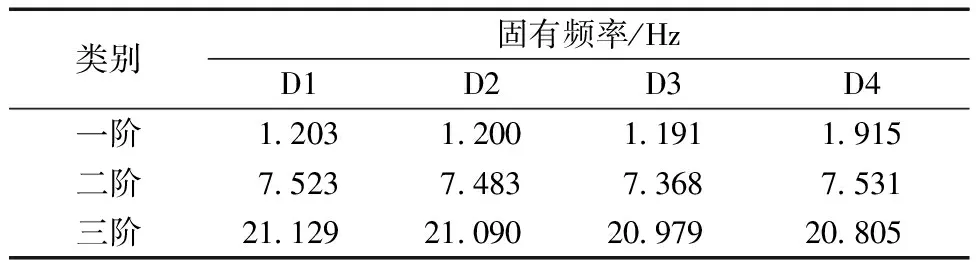
表3 悬臂梁在不同损伤工况下的固有频率

2.3 模态参数损伤识别

单损伤采用工况1、工况2和工况3,多损伤采用工况4进行算例分析。由于低阶模态可以更好地反映结构的整体动力特性,且与原始响应较为接近且平滑,同时受到噪声干扰的影响较小,因此在实际的损伤识别工作中,如果采用某个阶次的振动信号来识别结构损伤,通常建议选择低阶的振动信号,以减少损伤识别时的不确定性。因此,实际损伤识别应用中如果用某阶次的振动信号来识别和定位损伤时,通常第一阶次的被选用。通过数值模拟得到悬臂梁4种工况下的归一化一阶振型如图4所示。

图4 不同损伤程度下结构的位移模态Fig.4 Displacement modes of structures under different damage degrees

由位移模态分析结果可知,其在结构损伤前后的差异并不明显,很难判断损伤的位置,因此对位移模态进行小波分解(使用“coif1”小波基函数进行6层离散小波分解),用损伤后的小波系数平方减去损伤前的小波系数平方,得到如图5所示的小波系数平方差。由图5可知,结构损伤引起小波系数平方差曲线出现了显著的异常突峰现象,可根据突峰发生位置来定位损伤。从图5(a)可以看出,在悬臂梁单损伤D1～D3工况下均能够清晰地通过第8节点和第9节点的突峰判定第9号单元出现损伤,其结果与模型中预设损伤位置一致。特别是在悬臂梁发生10%较小的损伤时,小波系数平方差曲线的突峰值也比较明显,可以准确地识别出在第9号单元位置处存在损伤,且随着损伤程度的增加,小波系数平方差也越大。由图5(b)可知,在悬臂梁多损伤D4工况下,由小波系数平方差曲线可看出测点4与测点5、测点15与测点16有2个明显突峰,且因破坏程度一致,所以两处突峰大小相当。根据突峰位置,可判定在第5号单元和第16号单元的位置发生损伤。

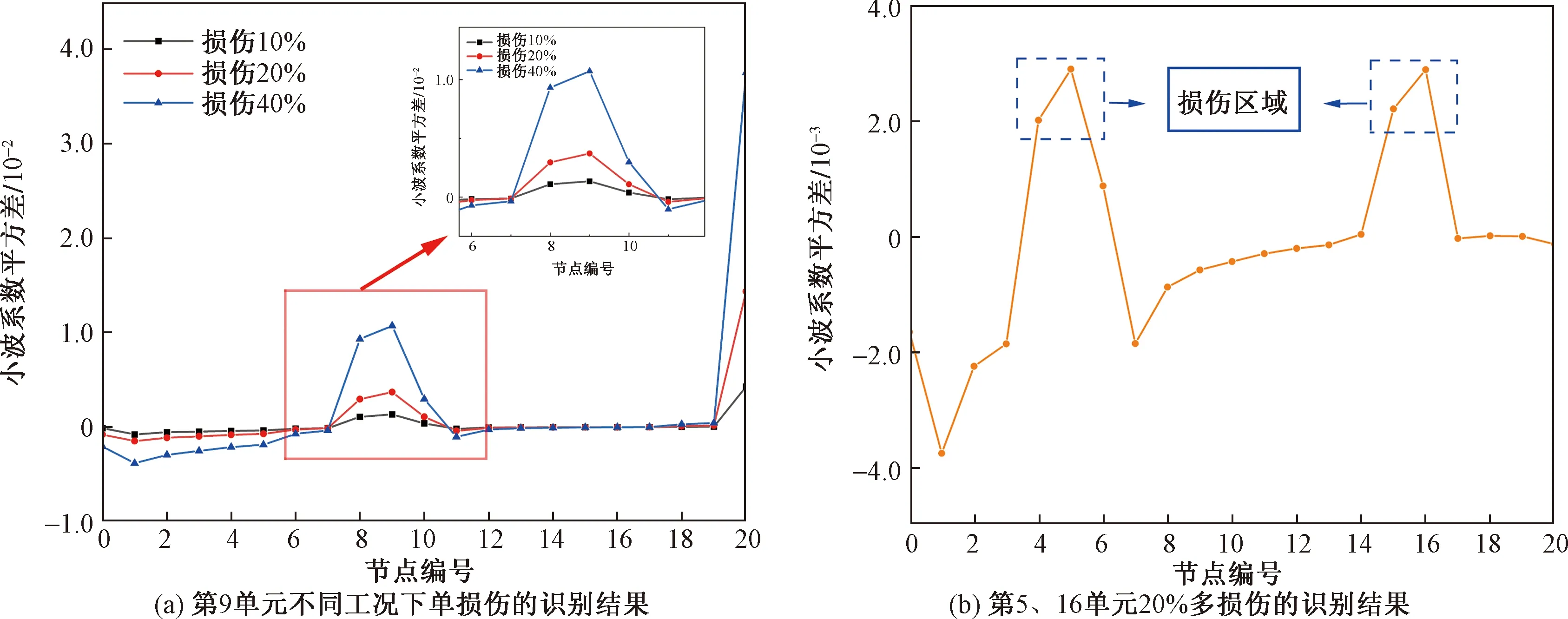
图5 4种工况损伤识别效果Fig.5 Damage identification result of four working conditions

3 悬臂竖梁试验验证

3.1 试验模型及测试方案

为进一步检验本文方法的可靠性,在实验室对一悬臂竖梁开展振动试验。悬臂竖梁模型与2.1节中数值模拟模型的几何尺寸及物理参数相同。悬臂竖梁模型试验布置示意图及测点分布如图6所示,试验以白色A4纸为背景,用黄色标点纸在悬臂竖梁正面一侧等间距布置20个测点,相邻测点的间距为50 mm,并将测点自下而上依次编号为P1～P20,以作为机器视觉系统动态位移追踪目标。在距离悬臂梁左侧70 mm处将动态激光测距仪固定在三角支架上,并将其调至激光正对悬臂梁的9号目标测点,以获取9号测点的振动衰减信号。在试验中,为避免光环境对机器视觉测量的影响,在悬臂梁上下两端分别布设了一台LED辅助光源以保证亮度均匀。同时在距离悬臂梁正面140 mm和155 mm处分别用相机三脚支架固定工业相机和索尼相机,并调整镜头方向使其与悬臂梁正面正交进行拍摄。在该距离下机器视觉采集设备(工业相机、索尼相机)能够对悬臂梁结构振动进行全域跟踪,进而通过模板匹配法对悬臂梁的20个目标测点进行追踪计算,以获取结构的多点位移时程曲线。

图6 悬臂梁试验模型Fig.6 Cantilever beam test model

试验中,采用人工激励方式在结构的6号测点处敲击,使其发生自由衰减振动,通过基于机器视觉获取的多点位移响应时程信号分析计算,提取结构位移模态。

3.2 试验仪器

试验中利用工业相机(a2A5328-4gmBAS)和商业相机(SONY FDR-AX40)同时采集悬臂梁的振动影像数据,并用激光测距仪(GOLTM-R603)和电脑(Msi GL62M)采集结构单点动态时程位移。其中工业相机的物面分辨率为360 pixel×460 pixel,帧率为50 帧/s;索尼相机的物面分辨率为1 080 pixel×1 920 pixel,帧率为50 帧/s;激光测距仪的采样频率为63 Hz。试验仪器型号及参数详如表4所示。

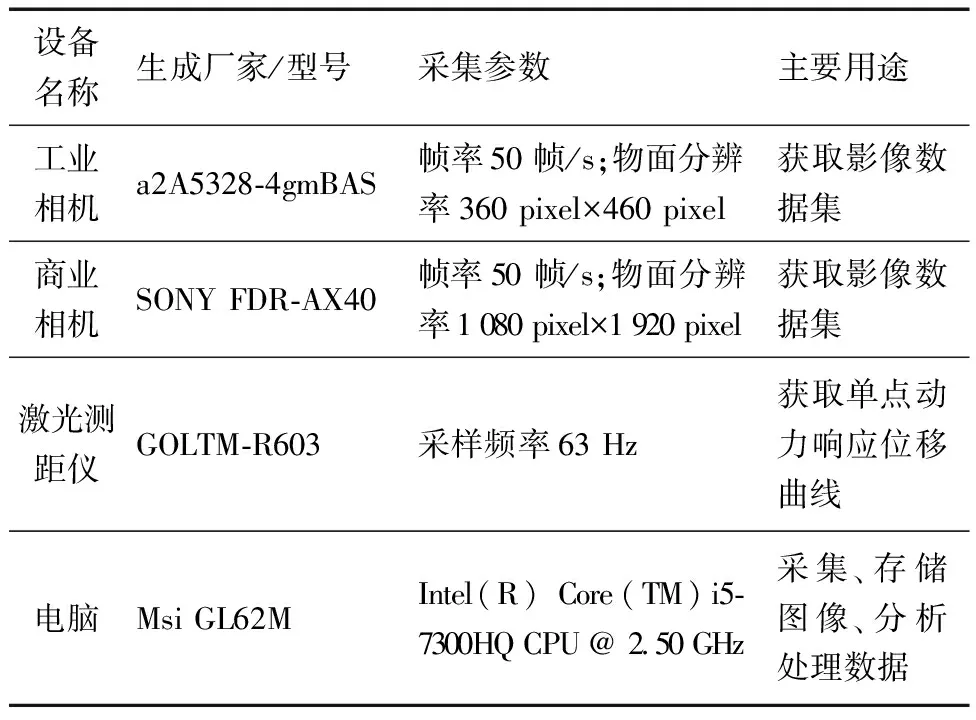
表4 试验测试传感器及采集设备参数

3.3 悬臂梁的损伤工况

由于裂缝深度d与截面刚度呈一次线性关系,所以实验通过设置深度为d,宽度为b=2 mm的矩形缺口用来模拟损伤,损伤程度S用裂纹深度d与梁宽度B之比表示,即S=d/B,图7所示为悬臂梁损伤试验的示意图,试验损伤工况与2.1节相同,具体损伤工况如表5所示。

表5 实验损伤工况

图7 悬臂梁损伤设置Fig.7 Damage of cantilever beam

3.4 时域分析

两种数据采集系统(基于机器视觉测量的系统和激光测距仪)记录了悬臂竖梁的振动衰减时程。如图8所示为基于机器视觉和通过激光测距仪获得的无损和工况1下测点9的位移时程曲线,利用测量的数据分析了动态特性,对比研究基于机器视觉的测量系统和激光测距仪的测量精度。从图8(a)可以看出3种仪器获得的时域振动衰减趋势吻合良好,但从图8(b)和图8(c)[图8(b)的5～10 s放大图]可以看出,第9号单元损伤10%的位移响应信号的激光测距仪与视觉测量前5 s内基本重合,而后5 s内的时程曲线出现了明显偏移,这是由于激光测距仪的采样频率不稳定导致的,从而也进一步凸显视觉测量采样稳定的优势。

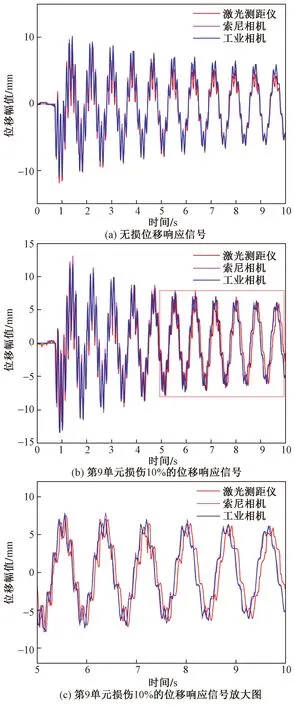
图8 悬臂梁在无损和损伤10%时的位移时程曲线Fig.8 Displacement-time curve of cantilever beam with undamage and 10% damage

3.5 频域分析

将无损和工况1下获取的第九测点振动衰减曲线进行频域分析,在频域空间中对比研究基于机器视觉系统和激光测距仪的测量精度。由图9可以看出,激光测距仪、索尼相机、工业相机在频域中吻合度高。

图9 不同工况下的频域对比分析Fig.9 Frequency domain analysis and comparison under different working conditions

对利用激光测距仪器、索尼相机和工业相机采集悬臂梁的振动信息进行频域分析,得到其在5种工况下第9号测点的第一阶和第二阶频率如表6所示。结果表明,一阶固有频率fa和fb的最大误差均为2.202%,二阶固有频率的fa最大为3.589%、fb最大为3.182%。

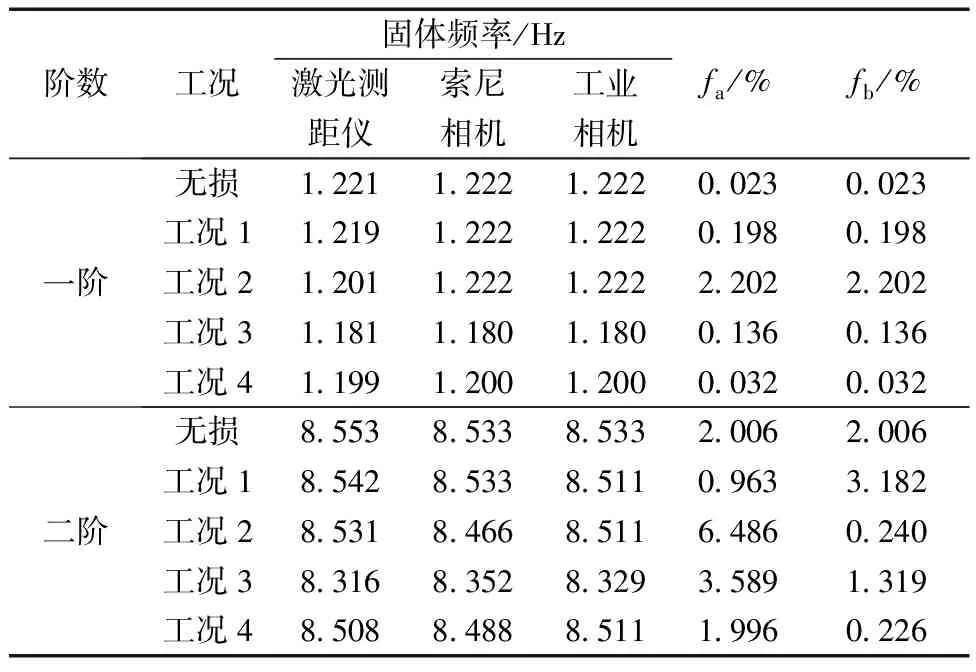
表6 不同工况下悬臂梁第9号测点前二阶频率

3.6 振型识别

傅里叶变换后的幅值谱上的峰值与结构模态是相对应的,通过拾取某测点位移信号FFT后振幅谱上的峰点,可以确定结构的各模态信息。其中幅值谱上峰值从左到右的序号代表相应的模态阶次,峰值的横坐标代表该阶模态的模态频率,纵坐标代表这个测点在该阶模态振型图上的幅值大小。振型图上的振动方向则依靠虚部谱和相位谱进行判断,若各个测点对应某阶模态的虚部谱上纵坐标符号为正,则确定幅值谱所取峰值纵坐标在振型图上的符号为正,反之取负。

首先将机器视觉方法获取振动衰减信号的幅值最大值作为归一化因子,接着,将该种测量方法的其余测点与归一化因子相比即可求出其振型坐标。

与商业相机相比,工业相机输出原始数据,其光谱范围往往比较宽,更适合高质量的图像处理算法,且图像未经过压缩,质量较高,更适用于机器视觉测量,有利于分析处理,因此下文将以工业相机为主要考虑对象。通过机器视觉测量方法获得的一阶振型如图10所示。可以看出,利用模板匹配法得到的模态振型与传统方法得到的模态振型有很高的吻合度,结果表明,非接触式影像测量获得的结构模态振型准确可靠。该方法为获取桥梁结构的模态参数和结构健康监测提供了一种新的手段。

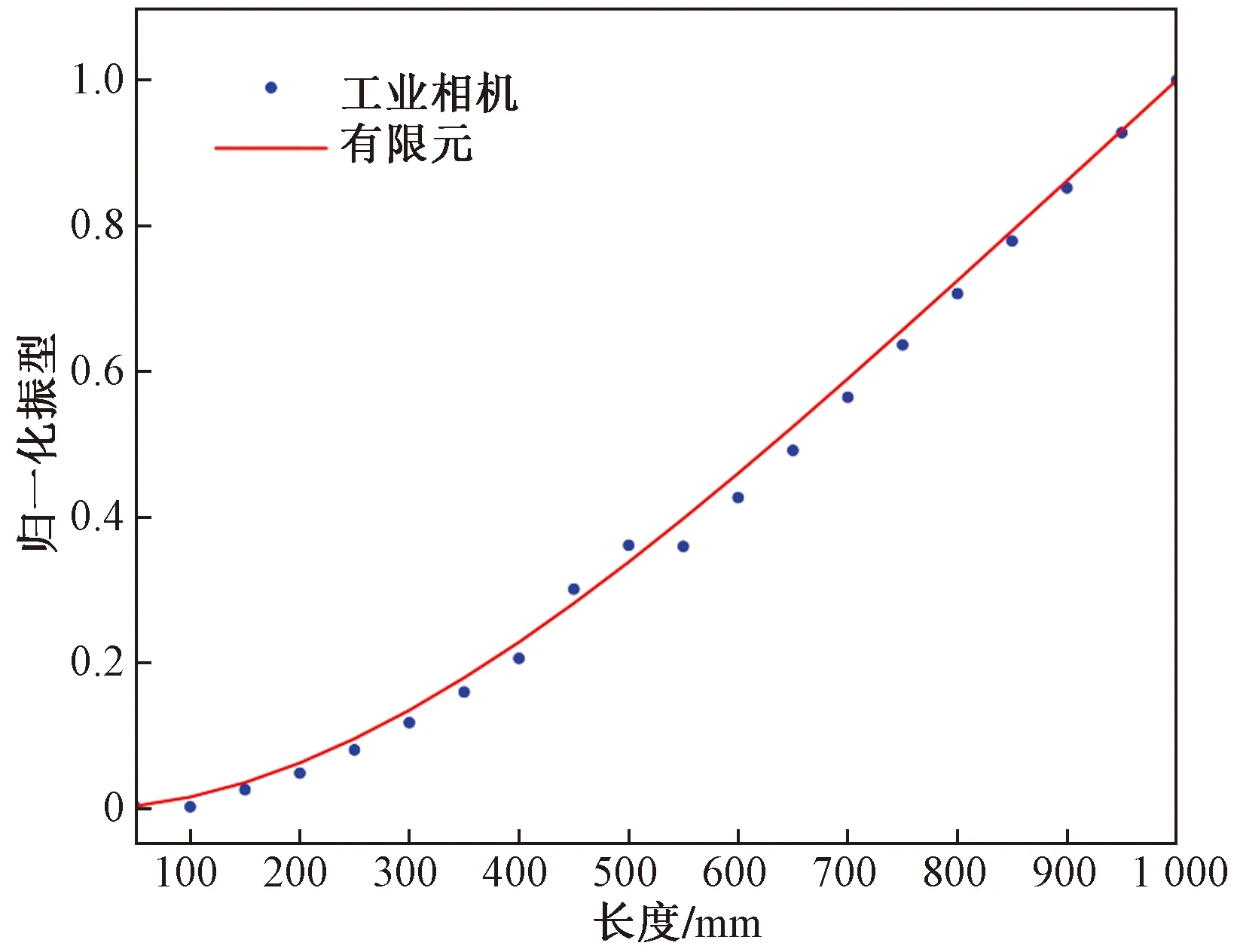
图10 无损工况下有限元和试验归一化位移模态对比Fig.10 Comparison of normalized displacement modes between finite element method and experiment under undamage conditions

3.7 模态参数损伤识别

通过小波系数平方差损伤指标对悬臂竖梁模型进行损伤识别,实验结果如图11所示,实验共设置4种损伤工况,小波系数平方差在D1～D3工况下产生一处突峰,在D4工况下产生两处突峰。从图11(a)中可以看出,小波系数平方差在节点8和节点9之间存在一处损伤,损伤发生于突峰对应的第9号单元,且随着损伤程度的增加,小波系数平方差也越大。从图11(b)中可以看出,小波系数平方差曲线在节点4和节点5之间,节点15和节点16之间位置处均有明显突变峰值出现,依据损伤指标小波系数平方判定悬臂竖梁对应的第5号和16号单元均有损伤,其损伤判定结果与预设损伤位置相吻合。

图11 试验各工况时损伤识别效果Fig.11 The effect of damage identification under various working conditions

此外,由于测试实验过程中会存在仪器、噪声以及操作上的多种不可避免的误差来源,为了确保该方法对损伤识别结果准确可靠,在工程实际中,测试时还需要对多组数据测量计算或者降噪处理以避免判断错误。

4 结论

提出了基于影像和小波变换的桥梁损伤识别新方法。该方法具有非接触、高效快捷、可多点监测提升振型空间分辨率和准确识别及定位损伤等优点。在实验室对悬臂竖梁振动进行机器视觉与传统传感器(激光测距仪)测量,并通过损伤试验和数值模拟分析验证了该方法对结构损伤识别的可行性和准确性,主要结论如下。

(1)图像序列包含了丰富的数字信息,基于数字图像处理技术能够有效地获取结构动力响应,通过悬臂竖梁振动敲击实验,分别从时域和频域的角度验证了该方法用于结构位移测量的可行性以及测量精度的可靠性。其中一阶频率最大误差为2.202%,二阶频率最大误差为3.182%;对全域测点的振动衰减信号快速傅里叶变换成功获取了结构的模态振型,与有限元结果高度吻合。

(2)通过小波基函数对位移模态进行六层离散小波分解,根据小波系数平方差的峰值能够精确地识别结构损伤位置,且其峰值随着损伤程度的增加而显著增加。

(3)在基于影像获取结构的频率和振型基础上,通过位移模态的小波系数平方差可以准确地定位识别悬臂梁的单损伤和多损伤,结果与预设损伤位置高度一致,损伤因子在损伤处峰值显著,具有良好的鲁棒性。