基于改进XGBoost的地震多属性地质构造识别方法
2023-11-06杨楚龙王怀秀刘最亮
杨楚龙, 王怀秀*, 刘最亮
(1.北京建筑大学电气与信息工程学院, 北京 102616; 2.华阳新材料科技集团有限公司, 阳泉 045000)
煤炭在现在以及将来很长一段时间仍为中国的最主要能源来源,是中国赖以生存和发展的物质基础[1]。进入21世纪以来,大型化和向深处掘进成为煤矿的发展趋势,许多煤矿的地质条件处于不稳定状态,而煤矿的地质构造会引起矿井突水、瓦斯爆炸、塌方等一系列安全问题[2-4]。地质构造的存在严重威胁着矿井生产的安全,为此急需解决地质构造位置的预测,为提高煤炭的产量和保证煤矿安全提供有力的支持[5]。地震属性可以用来预测地质构造,而这些地震属性可以从三维地震勘探成果数据体中提取出来[6-7]。地震数据经过一系列数学变换和处理,从中可以提取出关于地震波的几何属性、动力学属性、运动学属性和统计学属性,这些属性就称之为地震属性。地震属性经提取后对其进行分析利用,最后用来预测[8]。矿井中的地质情况十分复杂,影响地质构造的因素众多,利用单一的地震属性往往不能够准确地识别出构造,因此利用地震多属性融合技术十分有必要。
地震属性的研究早在20世纪90年代就开始了,何隆运[9]于1992年将波形合成追踪法融合地质属性,该方法建立了地震信息与地质信息间的对应关系,并利用此对应关系解决了许多复杂的地质问题,取得了良好的地质勘探成果。进入21世纪以来,随着机器学习和人工智能的蓬勃发展,地震多属性融合技术与各种算法的结合更加紧密。金龙等[10]将支持向量机(support vector machine,SVM)应用于地震属性融合,SVM是一种理论基础严密、鲁棒性强的机器学习算法,但是其在解决大数据量样本以及多分类问题上具有一定的局限性。丁峰等[11]用主成分分析(principal component analysis,PCA)根据主分量对多个地震属性进行排序,取前3个主分量进行RGB颜色融合,该方法可在一定程度上提高地震属性分析的效率。但是PCA属于“有损失”压缩,会损失一些有用的信息。杨久强等[12]把深度神经网络应用于地震属性的融合中,深度神经网络一般含多个隐藏层,理论上可以模拟任何的复杂函数,对模型的拟合能力十分强大,但是其容易出现过拟合、梯度爆炸的问题。上述研究虽然取得了一定的成果,但是仍然存在着属性选择较为单一、不能全面反映地质构造特征的问题。
在大数据时代,各行各业都面临着海量的数据,但是这些数据大部分都存在类别不均衡的问题。面对此类问题,传统的分类算法会自动地忽略少数类,并把少数类样本归类到多数类样本中以提高分类准确率[13]。例如,在二分类问题中,多数类样本的比例为98%,少数类样本的比例为2%,分类器即使把任意样本都预测为多数类,该分类器的准确率都可以达到98%。该分类器会导致大量的少数类被分为多数类,这种情况在一些特殊应用场所会造成严重后果。例如在医院的癌症诊断中,正常病例占大多数,而真正的病例只占少数,医生关心的是怎么把这些真正的病例识别出来,在这种情况下把真正病例判断为正常病例的代价非常大。类似的情况在电信诈骗检测、煤矿地质构造识别中也很常见。
在实际矿区中,构造体只占矿区的极少数部分,矿区大部分区域都为无构造,而目前关于地质构造识别的研究大都没有考虑这一因素。因此,在不平衡数据的情况下识别构造体具有重要的现实意义。
为了克服上述问题,现提出一种基于边界样本分类算法(boundary sample classification,BSC)的合成少数类过采样技术(synthetic minority over-sampling technique,SMOTE)算法BSC-SMOTE。BSC-SMOTE算法把处于正负样本边界的样本进行分类,只对“边界样本”进行合成,有效地避免正负样本边界模糊的问题。再用平衡后的数据集训练极限梯度提升(extreme gradient boosting,XGBoost)分类器,并使用贝叶斯优化(Bayesian optimization,BO)算法对该分类器进行超参数寻优,最后使用优化后的XGBoost分类器对构造体进行识别。
1 方法原理及其改进
1.1 SMOTE算法原理及其改进
合成少数类过采样技术(SMOTE)[14]是由Chawla等于2002年提出的,该算法的提出主要是为了改进随机过采样的弊端。随机过采样在合成新的少数类样本时,只是简单的对样本进行复制,这种简单的随机复制容易导致算法模型过拟合,不利于模型的泛化能力。而SMOTE算法不是对少数类样本进行简单的复制,而是根据一定的规则合成新的少数类样本。但是SMOTE在生成新样本时容易受样本集分布的影响,容易发生分布边缘化的问题,模糊样本的边界,如表1所示。

表1 SMOTE算法Table 1 SMOTE algorithm
SMOTE过采样的主要思想是:对样本集中每一个少数类样本Xi,计算其到其他所有少数类样本的欧式距离,然后对这些距离按从小到大的顺序进行排序,找出与其最近的K个样本,最后按照式(1)对该样本Xi与其K近邻Xk进行插值处理生成新的少数类样本Xnew,其中rand(0,1)表示0~1的随机数。SMOTE算法合成少数类的示意图如图1所示。

图1 SMOTE示意图Fig.1 Schematic diagram of SMOTE
Xnew=Xi+rand(0,1)|Xi-Xk|
(1)
SMOTE在生成新样本时容易受样本集分布的影响,发生分布边缘化的问题。对处于多数类样本与少数类样本分界处的少数类样本,在其选择K近邻样本时,这些邻居样本也分布在边界上,因此插值产生的新样本也处于边界上,反复迭代产生的新样本会模糊边界。极端情况下,如果有少数类样本分布于多数类样本之中,那么由它合成的新样本也会落在多数类样本之中。在这种情况下,样本集虽然得到了平衡,但是无形中给模型的分类增加了难度。
针对SMOTE算法容易模糊边界的问题,提出了基于边界样本划分的BSC-SMOTE算法,该算法强化了边界的界限,使之更有利于算法的分类,如表2所示。该算法的主要思想是:对样本集中每一个少数类样本Xi,计算其到其他所有样本的欧式距离,然后对这些距离按从小到大进行排序,找出与其最近的K个样本,如果其K个最近邻中全部为多数类样本则将此少数类样本划分为噪声样本,如果其K个最近邻中有一半以上为多数类则将此少数类样本划分为边界样本,如果其K个最近邻中有一半以上为少数类样本则将此少数类样本划分为安全样本。最后,只对边界样本按照式(1)进行插值处理,对安全样本和噪声样本不做处理。BSC-SMOTE算法合成少数类的示意图如图2所示。

表2 BSC-SMOTE算法Table 2 BSC-SMOTE algorithm
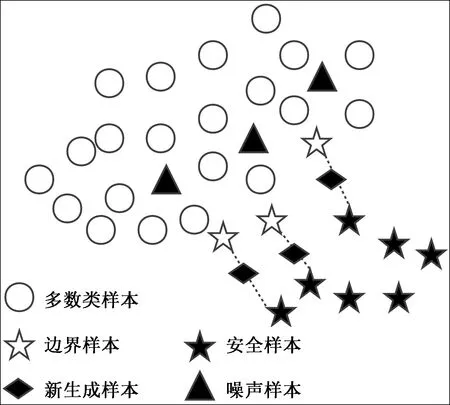
图2 BSC-SMOTE示意图Fig.2 Schematic diagram of BSC-SMOTE
1.2 XGBoost算法
在解决不平衡数据的分类问题时,通常有两种解决思路[15],一种是对数据集进行平衡,使得改造后的数据集均衡;另一种思路是对算法层面进行一些改进,例如使用集成学习算法。
XGBoost的全称为extreme gradient boosting,可翻译为极限梯度提升算法,是集成算法的一种。XGBoost是由陈天奇等[16]于2016年所提出的,自XGBoost提出以来,各种机器学习竞赛均由XGBoost算法所统治。XGBoost具有运行速度快,同时支持分类和回归、精度高、拥有正则化、防止过拟合等优点。XGBoost是在梯度提升树(gradient boosting decision tree,GBDT)的基础上进行改进的,GBDT只使用了一阶导数信息,XGBoost在GBDT的基础上还使用了二阶导数信息,并且XGBoost可以自己定义代价函数,其代价函数引入了正则项用于控制模型的复杂度,使XGBoost学习出来的模型更简单,泛化性能更高。其主要思想为:先训练一棵树,得到预测结果,把预测值和真实值的差值记作残差,用残差代替真实值。然后在第一棵树的基础上训练第二棵树,得到第二棵树的残差,用残差代替真实值,以此类推直到第K棵树,最后把K棵树的预测值加起来得到最终结果。
XGBoost是由k个基分类器集成的一个分类器,例如第t次迭代的树模型是ft(xi),有
(2)
(3)

表3 XGBoost常用超参数Table 3 XGBoost common hyperparameters
用BSC-SMOTE算法平衡后的数据集训练XGBoost分类器,得到BSC-SMOTE-XGBoost模型。
1.3 贝叶斯优化算法
贝叶斯优化(BO)是一种全局优化算法,具有高效性和鲁棒性的优点,能够在非常少的采样次数下快速找到全局最优解,因此被广泛地运用在超参数优化、机器学习模型优化、神经网络结构搜索等领域。贝叶斯优化算法的原理是通过贝叶斯公式,将先验分布和观测数据结合起来,计算后验分布,并不断更新后验分布,最终找到全局最优解[17]。贝叶斯公式为
(4)
式(4)中:f为待优化的函数;D为已知数据;P(f|D)为已知数据D的情况下,待优化函数f的后验概率;P(D|f)为函数f的似然函数,表示在函数f下,数据D出现的概率;P(f)为先验概率,表示对函数f的先验分布的假设;P(D)为归一化因子,用于将后验概率归一化为概率分布。通过最大化后验概率P(f|D),可以找到最优函数f*。在每次迭代中,贝叶斯优化算法使用已知的数据D来更新函数f的后验概率分布,然后根据后验概率分布选择下一个函数参数进行评估。这个过程不断迭代,直到找到最优的函数参数。
用贝叶斯优化算法对所得到的BSC-SMOTE-XGBoost模型进行超参数寻优得到BO-BSC-SMOTE-XGBoost模型,其中待优化函数f为XGBoost的目标函数obj。找到最优函数f*就找到了XGBoost的最优超参数组合。
2 地震属性融合与筛选
2.1 数据获取与分析
地震属性可以用来解释与预测地质构造,因此地震属性被广泛地运用在煤矿地质构造的识别。以山西新元煤矿三维地震勘探成果数据体为基础,提取出12种地震属性。这12种地震属性分别为:倾角、最小振幅、最大振幅、瞬时相位、瞬时频率、均方根振幅、方差体、相干体、曲率、主频、瞬时振幅和平均能量。这12种地震属性的最大值、最小值和平均值如表4所示。可知,各个属性之间极差以及平均值差异较大,加上各属性的量纲不同,如果直接对这些属性进行融合,各个属性之间的差异会影响最后数据融合的效果。为了消除各个地震属性之间的差异,就需要对属性进行数据标准化处理。采用离差标准化消除各个属性之间量纲的差异,并把各个属性通过线性变换映射到[0,1]。离差标准化的转换公式为

表4 地震属性的数据分布情况Table 4 Data distribution of seismic attributes
(5)
式(5)中:x为原始属性的值;min(x)为属性最小值;max(x)为属性最大值;x*为标准化后的属性值。
以经过标准化处理后的12种地震属性作为数据集的特征,以山西新元煤矿有限公司前方实际揭露的地质构造作为数据集的标签,由此构成数据集的特征和标签。数据集的标签为3类:无构造(标签记为0)、陷落柱(标签记为1)、断层(标签记为2)。其中断层破坏了煤岩体内部应力场的初始平衡状态,使煤层发生滑动位移,大规模的断层会造成煤矿停产和工作面搬家,甚至会造成透水、瓦斯突水等安全问题[18]。陷落柱会影响煤层分布的连续性及稳定性,同时陷落柱会对工作面的布置和推进产生巨大影响,导致工作面的开采效率大幅降低[19]。通过对矿方提供的数据进行分析,发现已揭露的矿区中,无构造区域占绝大多数,而断层和陷落柱只占一少部分。新元煤矿已揭露矿区数据分布情况如表5所示。
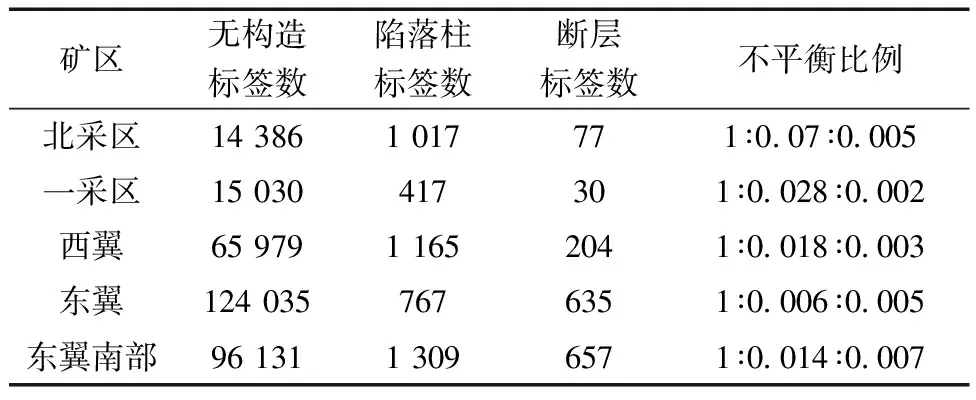
表5 已揭露矿区数据分布Table 5 Data distribution of exposed mining areas
由表5可知东翼勘探区无构造标签数最多,数据的不平衡程度最高,且断层和陷落柱较为发育,具有一定的典型性,故选取东翼勘探区作为研究区域。
2.2 地震属性优选
在选择特征时,如果特征选择偏少,模型学习不到足够的信息,会影响模型的效果。如果特征选择过多,其中可能存在着噪声,也不利于模型的学习。特征重要性是用来描述特征对于标签的重要性,特征重要性越大表明特征对于标签的贡献越大,反之特征对于标签的贡献越小。互信息法是一种用来衡量特征与标签相关性的过滤方法,互信息法既可以用于回归也可以用于分类,它的返回值在0~1,返回0证明特征与标签不相关,返回1证明特征与标签完全相关。互信息的计算公式为
(6)
式(6)中:X和Y为两个随机变量;x为随机变量X可能取的值;y为随机变量Y可能取的值;X和Y的边缘分布分别为p(x)与p(y),联合概率分布为p(x,y)。利用互信息法计算特征与标签之间的关系如图3所示。
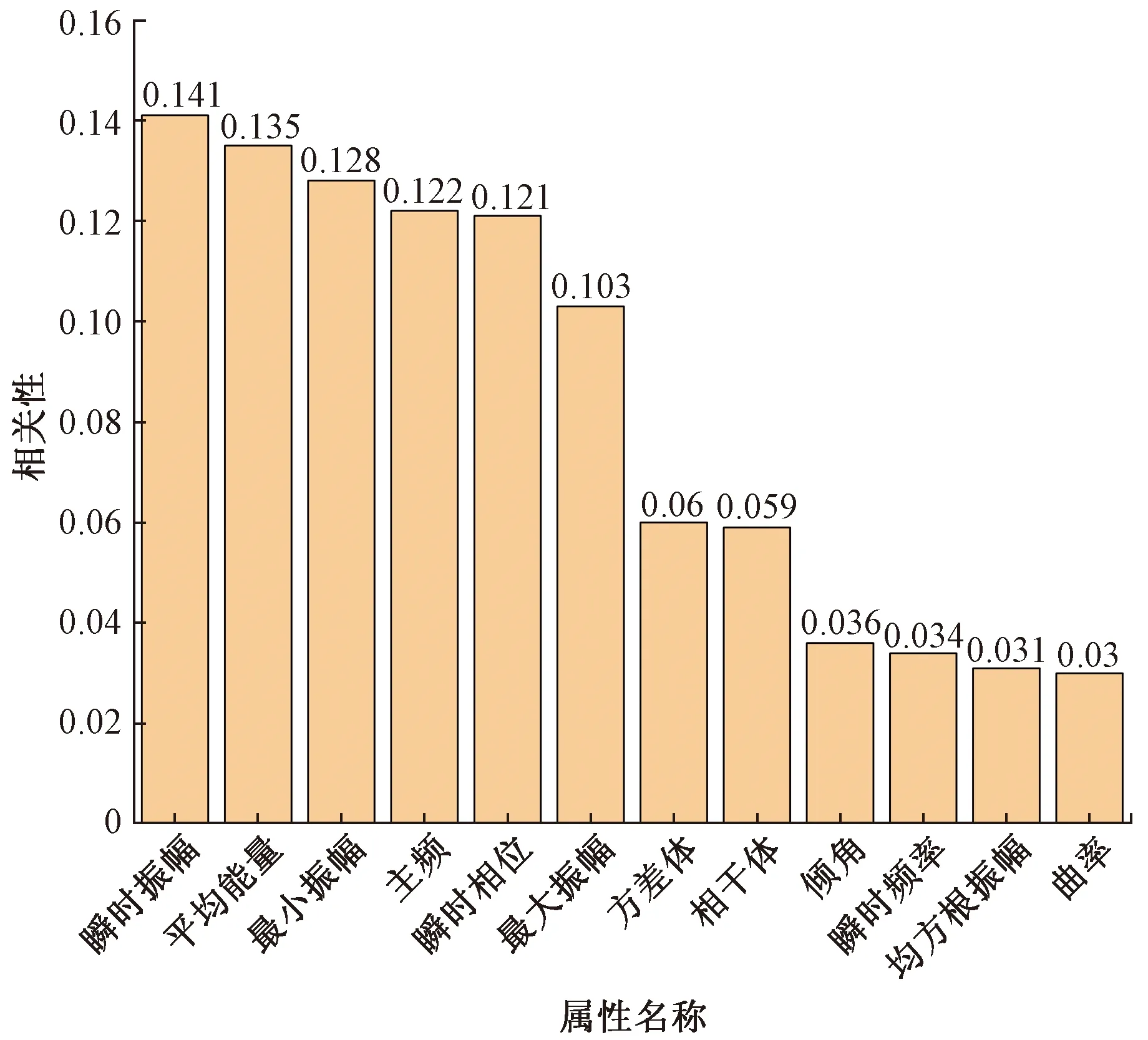
图3 特征相关性Fig.3 Feature correlation
如图3所示,所有的特征对于标签的相关性都大于0,证明所有的特征都与标签相关,其中瞬时振幅与标签的相关性最大为0.141。但曲率、均方根振幅等特征与标签的相关性比较低,为了找出真正对算法模型有效的特征,以特征相关性为变量画出学习曲线。首先以0~0.141为特征相关性的范围画出学习曲线,如图4所示,可以看出,当特征相关性阈值设为0.10左右时,分类算法的准确度可以达到最高。
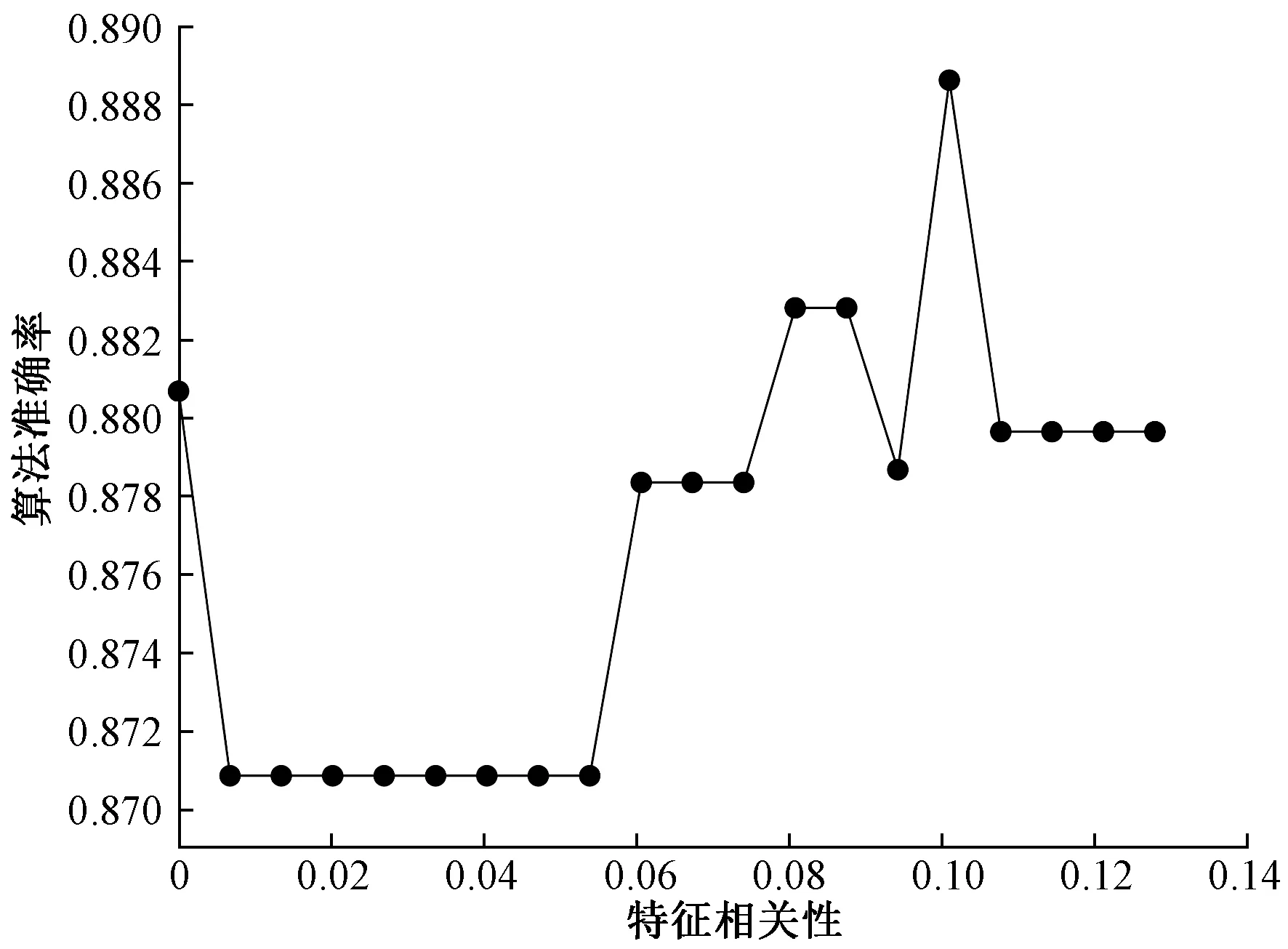
图4 大范围学习曲线Fig.4 Large scale learning curve
进一步缩小阈值范围,以0.09~0.11为范围画出学习曲线如图5所示。

图5 小范围学习曲线Fig.5 Small range learning curve
从图5可以看出,当特征相关性为0.102 5时,算法准确率达到最高,所以设置特征相关性阈值为0.102 5,即只保留相关性大于等于0.102 5的特征,小于0.102 5的特征全部舍去。通过属性筛选,最后只保留了瞬时振幅、平均能量、最小振幅、主频、瞬时相位和最大振幅这6个特征。
3 实验验证与分析
3.1 评价指标
通常情况下,分类器性能的好坏可以使用准确率(accuracy)作为评价指标,但是在数据集不平衡的情况下,单纯比较分类器准确率的高低没有太大的意义。因为准确率把多数类分类错误的代价和少数类分类错误的代价没有区分开,显然把少数类分类错误的代价比把多数类分类错误的代价要大。此时可以使用精确率(precision)、F1(F1score)和召回率(recall)这些更加科学的指标来评价模型,这些指标都是建立在混淆矩阵的基础上,混淆矩阵如表6所示。
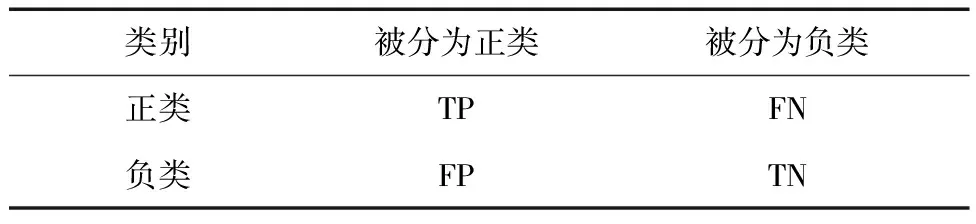
表6 混淆矩阵Table 6 Confusion matrix
精确率的定义是所有预测为正类的样本中真正是正类的比例,其计算公式为
(7)
召回率的定义是所有正确预测为正的样本占所有实际为正的比例,其计算公式为
(8)
F1同时兼顾了精确率和召回率,是两者的调和平均值,F1的值越大表示分类器越有效,其计算公式为
(9)
3.2 模型构建
首先把东翼勘探区数据集按照7∶3分成训练集和测试集,对训练集运用BSC-SMOTE算法进行平衡,然后用平衡后的训练集训练XGBoost,再用贝叶斯优化算法对XGBoost进行超参数寻优,最终形成了BO-BSC-SMOTE-XGBoost模型。贝叶斯优化算法寻优的过程和模型训练过程如图6和图7所示。

图6 贝叶斯优化过程Fig.6 Bayesian optimization process

图7 模型训练过程Fig.7 Model training process
如图6所示,当迭代次数为30次时,模型取得了最小误差值,即XGBoost的目标函数obj取得最小值,此时模型对应的超参数为最优超参数组合,并且如图7所示此时模型的准确率最高,最优参数组合如表7所示。

表7 最优超参数组合Table 7 Optimal hyperparametric combination
将改进后的XGBoost算法与KNN、随机森林,SVM以及未改进的XGBoost算法进行对比,对比结果如表8所示。

表8 算法对比(东翼)Table 8 Algorithm comparison (Dongyi)
通过实验对比发现,提出的改进XGBoost算法在精确率、召回率、F1均有明显的提升,改进XGBoost算法模型的预测精确度为0.95,比未改进的XGBoost算法提高了0.16,比KNN、随机森林和SVM等传统算法提高了0.15以上。把算法模型获取的模型参数应用于东翼勘探区,得到东翼勘探区构造预测结果,并把预测结果经软件可视化得到如图8所示的预测构造图。经过与东翼实际揭露构造(图9)对比,可以发现预测构造的数量与实际构造的数量基本相同,且预测构造的坐标与实际构造的坐标吻合,说明本文算法模型能够克服类别不平衡的影响,较为精确地识别出地质构造。
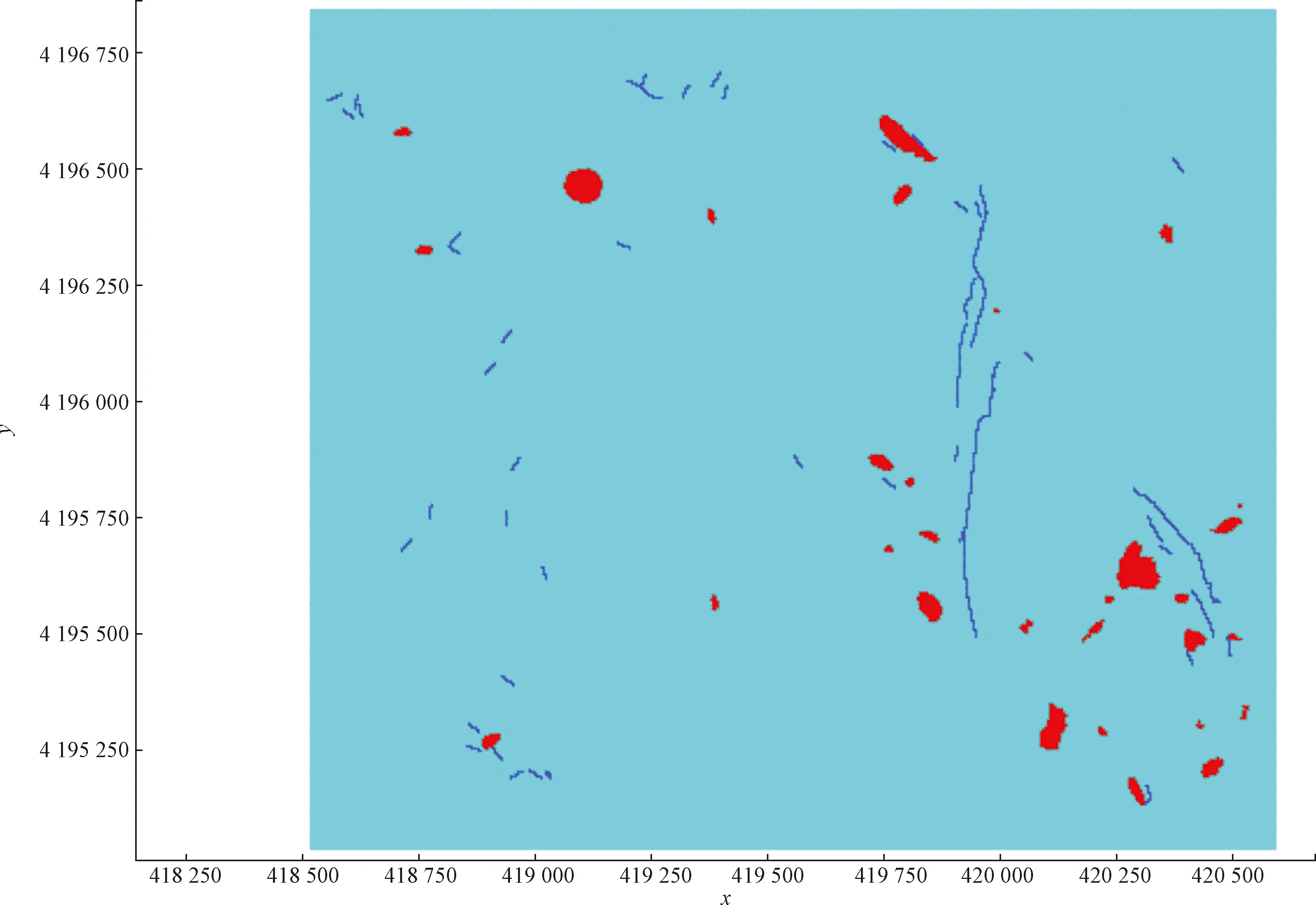
浅蓝色区域为开采的范围;红色区域为陷落柱;深蓝色区域为断层
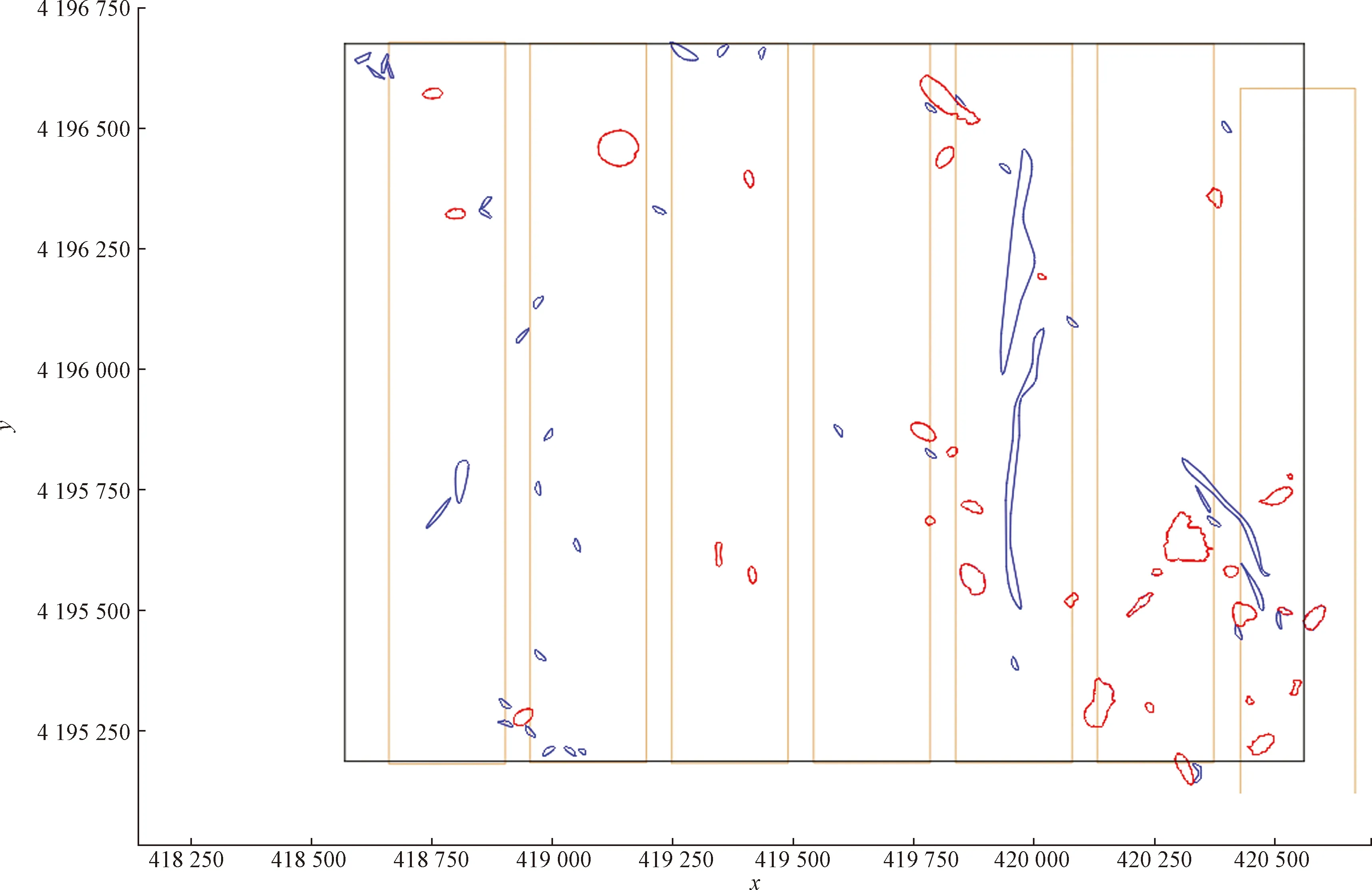
棕色线条为开采的巷道;红色线条围成的区域为陷落柱;蓝色线条围成的区域为断层
4 结论
为研究不平衡数据条件下的地质构造体识别的问题,通过理论分析与实例验证。得出以下结论。
(1)煤矿的地质构造体(断层,陷落柱)是造成煤炭减产,煤矿事故频发的因素之一,预测煤矿的地质构造体具有重要的现实意义。通过对三维地震勘探成果数据体的地震属性进行融合分析后可以用来预测构造体。
(2)在众多地震属性中,不是所有的地震属性都对算法模型的构建有用,筛选出与标签相关的属性能够提高模型的准确率和效率。
(3)实际的应用中,构造体的数量只占勘探区的极少部分,这种分布的不均衡会直接影响算法模型的分类性能,可以通过改善这种分布的不均衡来提高模型的分类性能。
(4)XGBoost具有运行速度快,同时支持分类和回归、精度高、拥有正则化、防止过拟合等特点。贝叶斯优化算法考虑之前的参数信息,不断地更新先验,能够又快又准地找到XGBoost的最佳超参数组合。
