翅片间距对管翅式相变储热单元储热特性的影响
2023-11-06王纾禾栾茹王一波国建鸿赵勇雷鸣宇
王纾禾, 栾茹, 王一波, 国建鸿*, 赵勇, 雷鸣宇
(1.北京建筑大学电气与信息工程学院, 北京 102616; 2.中国科学院电工研究所, 北京 100190)
近年来,随着化石燃料的消耗,为清洁低碳的可再生能源创造了发展机遇[1]。中国太阳能资源丰富,但由于其具有不稳定、易受天气影响的特点,光伏出力和负载需求在时间上不匹配,电能存储成本较高,导致光伏发电利用率低,存在严重的弃光问题。光伏-热泵热电联供系统实现就地消纳光伏的同时为建筑物供暖提供了更加清洁的热源。相变储热技术是热电联供系统中热电解耦的关键一环,其与热泵的结合为建筑物供暖提供了更节能成本更低的选择,已有众多学者围绕热泵-储热的综合系统展开研究,冯国会等[2]采用TRNSYS和实验相结合的方式分析热泵与太阳能耦合的相变储热系统的运行情况,研究发现该系统中热泵机组的性能系数(coefficient of performance,COP)与普通能源系统相比提升了16.67%左右,证明复合式能源系统更加高效、节能。闫泽滨等[3]设计了以空气源热泵作为相变储热供暖的辅助热源的太阳能-相变储热空气源热泵复合供热系统。胡文举等[4]提出了将相变储热装置作为辅助热源的空气源热泵系统。上述研究表明热泵与太阳能耦合的相变储热装置综合供暖系统可有效提高热泵系统的供热性能,提高太阳能供热系统灵活性与稳定性,并证实了该复合系统在供暖中的可行性与可靠性。
储能技术有效发挥削峰填谷的作用,减少了可再生能源波动和间歇带来的弊端[5]。在众多热能存储技术中,相变储热因储热密度高和输出温度近似恒定的特点越来越受到重视[6]。因此对储热装置性能的设计与测试具有急迫性和必要性。
相变材料导热性能普遍较差,从而限制了相变储热装置的应用[7],因此大量学者对其强化换热进行研究。李芃等[8]在光管管壳式换热器及内管上加纵向直肋以提高导热性能,研究表明加装肋片后熔化时间与光管相比缩短了4倍多。Yang等[9]在套管式储热单元加装了环形翅片,并对其熔化过程进行数值模拟,结果表明加装环形翅片后可使相变材料的熔化时间缩短了65%。林道光等[10]对内翅式套管相变蓄热器蓄热过程进行数值模拟,研究表明翅片个数、高度和厚度的增加都能促进强化换热,但强化换热作用均会渐趋平缓。Wu等[11]的研究表明增加翅片长度和降低翅片高度可以显著缩短熔化总时间,并综合考虑了翅片位置对熔化和凝固过程中温度分布不均匀的影响,提出了不同翅片长度对应的最佳翅片位置。以上研究说明加装翅片是强化换热的一种主要手段,但这些对强化换热的研究仅证明了在其实验工况下的强化效果,缺乏对更多工况的定量分析,未综合考虑供暖运行参数对储热性能的影响,且大部分数值模拟基于二维物理模型,仅考虑了轴向流场及温度场的变化,甚至忽略了自然对流,无法真实反映翅片对系统的强化作用。且以往对热泵与相变储热复合系统的研究大多为两种模式互为辅助热源的可行性研究,对复合系统内储热装置的强化换热及其在热泵工作温区的换热特性研究并不充分。
减小翅片间距可以提高介质的导热速率[12],占据介质的体积,从而降低换热量,另一方面翅片过多会提高制造成本,翅片间距设计需同时考虑换热效果和经济可行性。为解决以上问题,更好地分析翅片间距对相变储热单元性能的影响,现以光伏供电热泵产热并结合相变储热设备的热电联供系统为研究背景,采用FLUENT对管翅式相变储热单元进行三维建模,根据前已述及的研究成果选择4种翅片间距结构,对该模型相变材料熔化过程进行数值模拟,并考虑相变材料的自然对流因素。基于对复合系统中储热单元储热特性研究的缺乏,首先数值模拟以热泵为热源时不同翅片间距模型下相变材料的换热特性;进而分析不同供暖运行参数——进水温度、流量对储热单元换热特性的影响规律,从而获得在改变其翅片间距过程中所呈现的储热量的变化趋势,特别是储热时间与储热量之间的关联性,这对于管翅式相变储热单元的结构优化设计至关重要。最后对于上述仿真结果进行实验验证。
1 模型建立
1.1 物理模型
相变储热单元是一个长为800 mm、宽为500 mm、高为100 mm的铝合金箱体,如图1(a)所示,主要由外壳、相变材料(phase change material, PCM)、翅片铜管和换热流体(heat transfer fluid, HTF)组成,选用铜作为管材和翅片材料以提高导热性。设计了4种翅片间距的模型,以研究不同翅片间距模型的换热特性。相变材料使用复合CH3COONa·3H2O-KCl,通过差示扫描量热法(differential scanning calorimetry,DSC)测得其基本属性,物性参数见如表1所示。对于储热过程,高温的HTF水从管内流过,PCM受热熔化温度逐渐升高至相变温度,实现相变储热。

表1 相变材料物性参数Table 1 Physical properties of phase change materials

图1 物理模型Fig.1 Physical model
为得到PCM内部温度变化过程,在Fluent内对YZ平面建立温度监测云图,自动保存时间间隔为30 min;并对7个特征点的温度变化进行监视,数据保存周期为一个步长,特征点分布如图1(b)所示,分别在离地30、50、70 cm处,距进水口储热箱体壁面Y方向的50 cm(T1,T3,T5)、20 cm(T2,T4,T6),选取管壁位置T7作为与内部PCM温升的比对点。
1.2 数学模型
为简化数学模型,进行了如下假设[13]。
(1)熔融的相变介质的流体流动是牛顿的、层流的、不可压缩的,考虑相变区域自然对流,采用Boussinesq 近似[14]。
(2)存放相变材料的箱体为连续、各向同性且均匀的。
(3)相变材料在给定温度内只发生固液相变,不存在过冷及性能衰减。
(4)储热器外壁面设置为绝热边界条件,忽略系统对外热损失。
(5)相变材料在固态及液态状态下比热容不发生变化。
考虑了温度对密度产生的影响,相变材料的密度采用Boussinesq假设近似,熔化区任意一点的密度为
ρ=ρ0-ρ0f(T-T0)g
(1)
基于以上假设,传热流体区域和相变材料区域的能量流动受三大守恒定律共同约束。
质量守恒方程为

(2)
动量守恒方程为

(3)
能量守恒方程为

(4)
式(4)中:
(5)
(6)
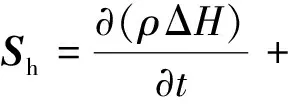
(7)
H=ΔH+h
(8)
ΔH=βL
(9)
式中:P为压力,Pa·s;U为达西表观速度,m/s;f为热膨胀系数,K-1;ρ0为PCM常温(20 ℃)下密度,kg/m3;T、T0分别为实际温度与初始温度,℃;g为重力加速度,kg/N;V为x,y,z各方向的速度分量,m/s;μ为动力黏度,Pa·s;Si为基于焓-孔隙率法在糊状区减少的动量方程的源项[15];Sh为由于固相材料的存在产生压降作为能量方程源项;Amush为糊状区常数,取Amush=105;ε为很小的常数,取0.000 1,避免计算时分母为零;β为液相体积分数;Tsolid和Tliquid分别为固相与液相的温度,℃;H为相变材料总焓值;ΔH为相变潜热,kJ/kg;h为显热焓值,kJ/kg;L为相变材料完全熔化潜热,kJ。
1.2.1 数值计算方法
由于相变问题是伴随着吸收或放出潜热的强非线性边界移动问题,无法使用近似法求解,采用基于有限体积法的ANSYS FLUENT分别建立翅片间距为λ、2λ、3λ、4λ(λ=10 mm),单边片高均为25 mm的相变储热单元计算模型。考虑翅片的高宽比较大,模型结构复杂且存在多域计算,采用Fluent Meshing绘制非结构化混合型网格,4种翅片间距模型网格的最大偏移量依次为0.55、0.58、0.44、0.45,均小于最大限度0.85,符合计算要求。
选取3D双精度、压力基、非稳态求解器,考虑求解域间传热,将流体域的自然对流视作层流,并采用基于焓-孔隙率[16]的熔化与冷凝模型对相变材料的熔化过程进行仿真。该模型优点在于将复杂的固液边界移动问题用多孔介质的孔隙率代替,简化了计算难度。松弛因子均设为10-6,分别选取5、10、15 s作为时间步长进行计算,由于对仿真结果影响不大,最终计算时间步长设定为10 s,考虑到光伏出力时间及实际供暖时间,储热过程设定为8 h。
1.2.2 初始条件及边界设置
为模拟实际实验初始温度,将全计算域的初始温度设为35 ℃。
T|t=0=Tinitial
(10)
式(10)中:Tinitial为求解域初始温度。
所研究的实验模型共有如下三类边界条件。
(1)入口边界。设定为质量流量入口,模拟实际实验流量0.6 m3/h,即0.166 7 kg/s;商用空气能热泵供暖出水温度范围一般为35~55 ℃,有部分产品可以最高达到60 ℃,因此仿真进水温度设置为55 ℃,对于探究不同供暖参数对换热特性影响的数值实验,需改变入口条件。
(2)出口边界。设为压力边界条件,回流比例设为1。
(3)壁面边界。将翅片外表面与PCM接触壁面、水管外侧与PCM接触壁面及水管内侧与HTF接触壁面均选用耦合边界条件,对应壁面边界条件为
(11)
储热单元的外壁为不锈钢材料,不考虑外壁面散热,设为绝热壁面作为边界条件,即
(12)
式中:t为实验时间,s;Tpipe-outside、Tpipe-inside、Tfin、TPCM、Twater、Tw分别为水管外壁面温度、水管内壁面温度、翅片温度、介质温度、进水温度及外壁面温度,℃;k为壁面的导热系数,W/m℃。
2 模拟结果及分析
2.1 相变储热过程特性分析
对储热单元的储热过程进行分析,以翅片间距为3λ,进水水温为55 ℃,进水流量为0.6 m3/h的仿真为例。
图2为介质内特征点温度变化趋势,第一阶段各点由环境温度快速上升至相变温度50 ℃,为固态显热储热;第二阶段特征点达到相变温度后,以潜热方式储热,该段时间介质温度变化平缓;第三阶段为液态显热储热,PCM相变完成后温度逐渐升高至与换热流体平衡的温度至储热结束。可以看出,位于50 cm处介质的熔化先发生,30 min内温升迅速,达到相变温度后,温度增长缓慢;20 cm处由于没有翅片,导热性较差,温升过程滞后30 min左右。
图3为液化率随时间变化折线图,液化率随时间增加,前300 min内增长迅速,曲线斜率大,熔化过程快;随后增长速率逐渐降低,可直观看出,在360 min左右液化率达到了97%,曲线趋于平缓,液化率增幅很小。

图3 PCM液化率变化曲线Fig.3 PCM liquid phase volume fraction variation curve
PCM内部相变过程较为复杂,且已忽略热损,根据热量守恒,PCM的瞬时换热功率由换热流体进出口温度计算,公式为
PQ=cpm(Tin-Tout)
(13)
式(13)中:cp为换热流体水的比热容,取4.2 kJ/(kg·℃);Tin为当前时刻进水温度;Tout为当前时刻出水温度;m为入口质量流量。
图4为PCM与HTF间换热功率随时间变化曲线,在熔化前10 min内换热功率最高达到14 kJ/s,由于初始温度与HTF温度相差较大,PCM为固态,热量以导热方式传递,故翅片周围介质温升较快;PCM液化率逐渐增加,相变材料熔化后液态密度减小,向上方移动,自然对流促进PCM熔化;300 min左右PCM液化率达到90%,传热管与PCM间温差减小,此时换热功率减小至0.5 kJ/s,换热功率曲线逐渐趋于平坦,360 min左右换热功率减小至0.1 kJ/s。

图4 换热功率变化曲线Fig.4 Heat transfer power variation curve
2.2 不同翅片间距的强化换热效果分析
图5为不同翅片间距在55 ℃,0.6 m3/h工况下的PCM平均液化率曲线,可以看出4组翅片尺寸模型的液化率随时间变化规律一致,均为先增大再减小,且达到90%后逐渐趋于一条直线,剩余10%左右PCM位于边缘处。
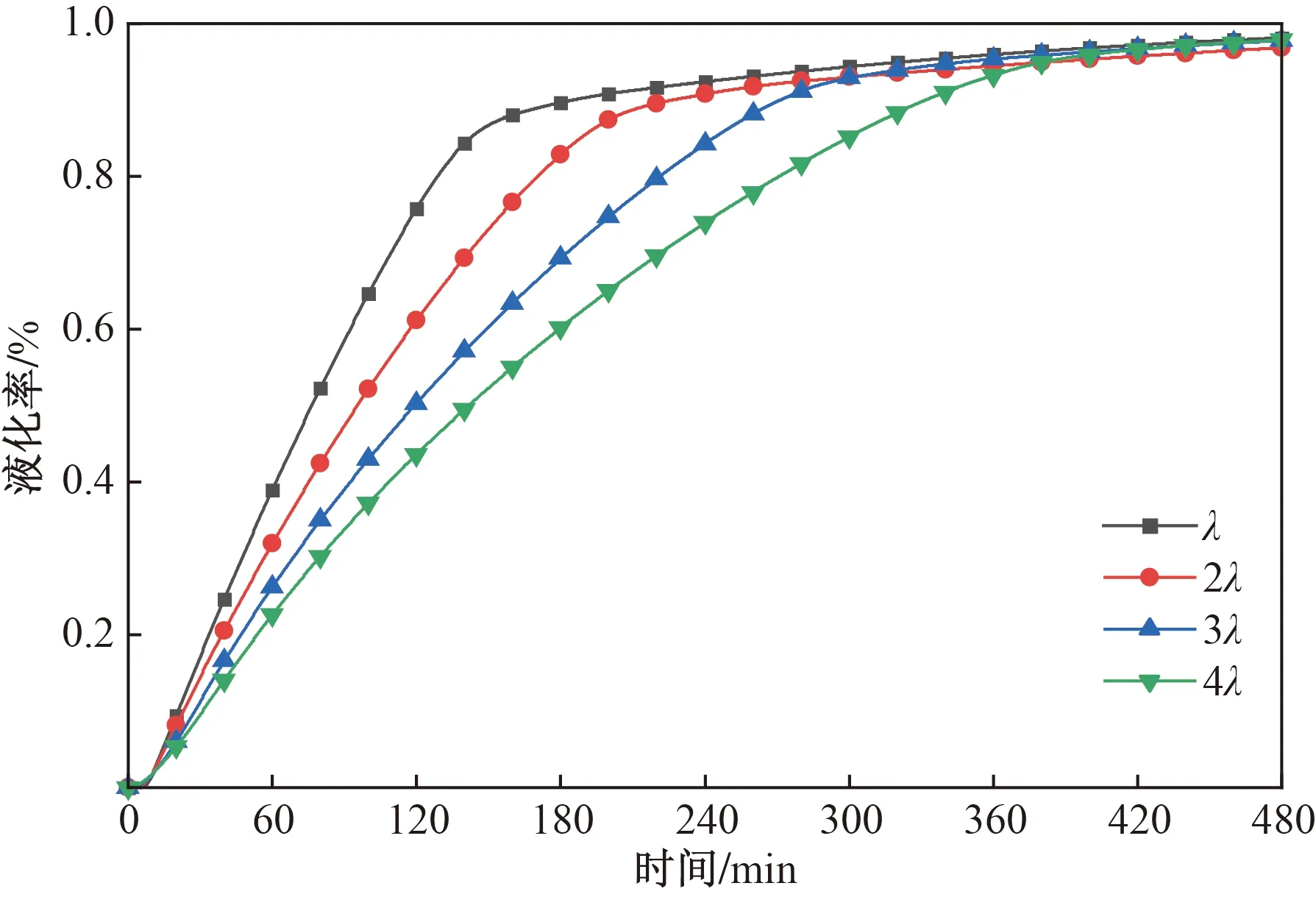
图5 不同翅片间距PCM液化率曲线对比Fig.5 Comparison of PCM liquid phase volume fraction variation curve under different fin spacing
对于不同翅片间距的模型,随着翅片间距减小,液化率曲线在熔化初期越陡峭,到达90%用时越短,具体数据如表2所示,翅片间距为λ~4λ熔化至90%用时分别为332、271、226、185 min,与翅片间距为4λ模型相比,λ模型缩短79.46%的时间。
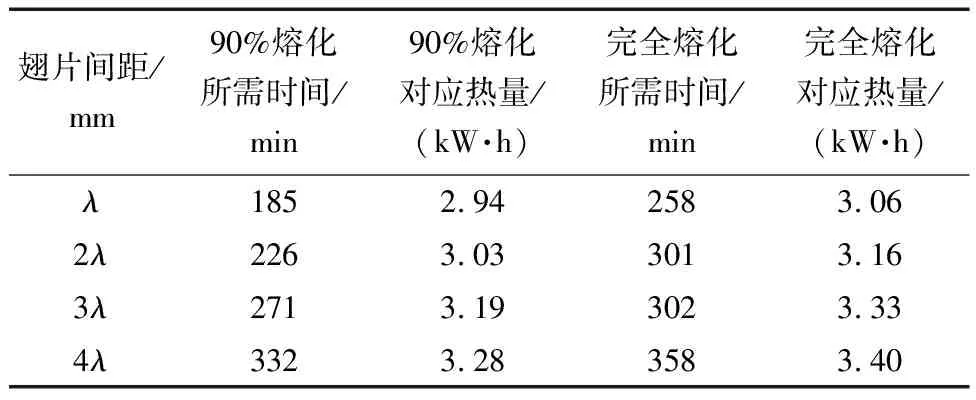
表2 熔化时间及储热量对比 Table 2 Comparison of melting time and heat storage
图6为不同翅片间距在储热300 min时相变介质XY平面的内部温度分布情况,在该时刻翅片间距为λ和2λ模型已完全熔化,如图6(a)和图6(b)所示,边缘处最低温度已达到相变温度,两侧没有翅片干预温升缓慢,是该模型的熔化“死区”,导致PCM完全熔化缓慢。如图6(b)和图6(c)所示,HTF从最上方管路进入,由于HTF在流动过程中热量不断消耗,PCM随水流方向的温度逐渐降低,越接近出水口处HTF的温度越低,周围PCM温升更加缓慢。整体来看翅片间距对温升影响显著,随着翅片间距的减小,PCM内部温度分布越均匀,边缘处温度越高。
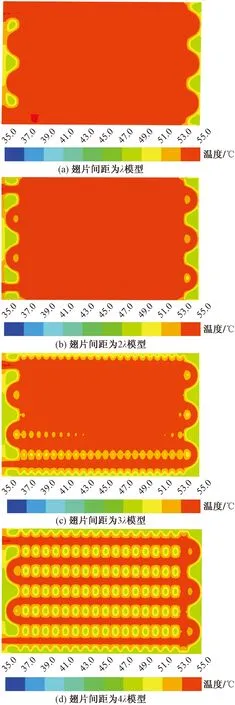
图6 YZ平面温度云图对比Fig.6 Comparison of temperature cloud diagram in the YZ plane
相变储热各阶段热量由式(14)计算,公式为
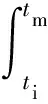
(14)
式(14)中:ti、tm、tf分别为开始储热时间、开始相变时间和储热结束时间,s;m为相变材料质量,kg;ΔT为PCM的平均温度与翅片平均温度间的温差,℃。
考虑相变机理的复杂性,通过对换热功率积分,求得该时段的总储热量为

(15)
图7为不同翅片间距储热量随时间变化曲线,由图可知储热量变化趋势与液化率相似。对于固定工况的四组模型而言,翅片间距越小的模型,在熔化初期的换热功率越大,熔化用时越少,储热量由于翅片间距减小挤占了PCM的体积的缘故而降低。翅片间距为λ、2λ、3λ、4λ模型在储热8 h后储热量分别达到了3.23、3.28、3.56、3.66 kW·h,与λ模型相比,储热量分别增加了1.55%、10.22%、13.31%。

图7 不同翅片间距储热量曲线对比Fig.7 Comparison of heat storage curves under different fin spacing
2.3 供暖运行参数对不同翅片间距换热特性影响
强化换热的实际研究意义在于提高单位时间的换热速率。由式(13)知换热功率受质量及温差影响,考虑到制造成本及实际情况,选取翅片间距为2λ及3λ模型进行数值模拟,并通过实验验证数值计算的准确性。
2.3.1 进水温度对换热特性影响
为研究不同进水温度对换热特性的影响,在相同进水流量下,共设4组进口水温:55、60、65、70 ℃进行仿真实验。
图8为两组翅片间距在不同进水温度下相变材料平均液化率曲线,与0.6 m3/h,55 ℃工况下一致。整体而言,翅片间距为2λ模型的熔化速率在各个工况下均更快,在各工况下,翅片间距为2λ模型比3λ模型完全熔化时间依次缩短了14.81%、19.73%、20.41%、20.12%;同一种结构随进水温度增加,PCM在相同时刻的液化率提高,熔化率达到90%的时间也大大缩短,液化率达到90%的时间分别为76.67、96.33、131.33、215.67 min,与进水温度为55 ℃的工况相比,2λ模型提高进水温度后熔化至90%的时间分别减少了39.10%、55.33%、64.45%;翅片间距为3λ模型达到90%的时间分别为90、120、165、270 min,与进水温度为55 ℃相比,时间分别减少40.25%、56.69%、65.77%。由式(14)可知进水温度增加后,增大PCM与HTF的温差,提升了换热系数,从而提高换热功率,增加单位时间换热量,加速PCM熔化。

图8 不同进水温度PCM液化率曲线对比Fig.8 Comparison of PCM liquid phase volume fraction variation curve under different inlet water temperatures
图9为两组翅片间距模型8 h的储热量对比,可明显看出翅片间距为3λ模型储热量更多,在55、60、65、70 ℃工况下翅片间距为3λ模型比2λ模型储热量依次增加6.06%、7.23%、7.73%、7.94%;总储热量随进水温度升高而增加,与进水温度为55 ℃工况相比,升高进水温度后翅片间距为2λ模型储热量依次增加6.73%、12.02%、17.27%,3λ模型依次增加7.91%、13.79%、19.35% ,进水温度的提升,提高了液态显热,使总储热量增加。
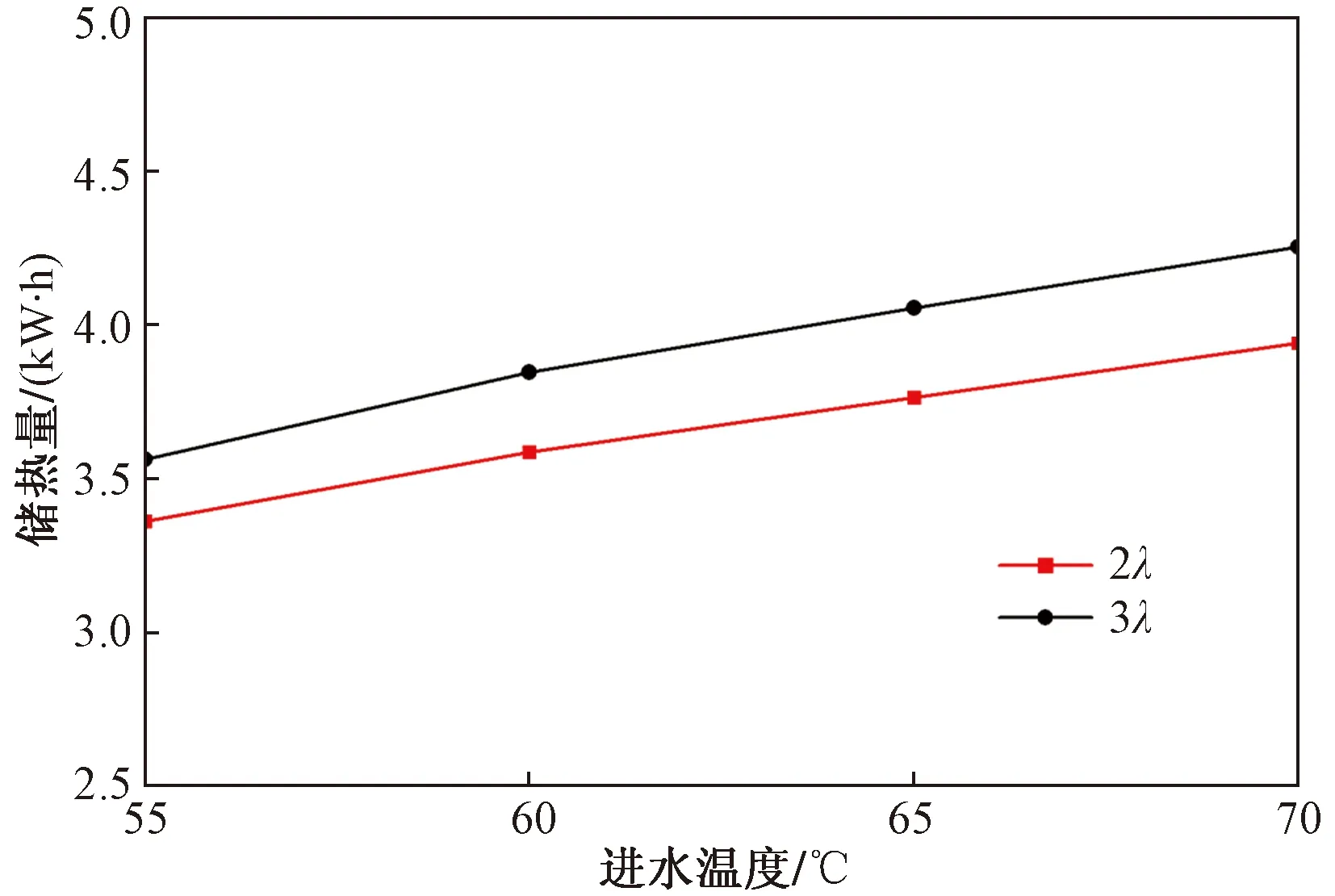
图9 不同进水温度储热量对比Fig.9 Comparison of heat storage under different inlet temperatures
2.3.2 流量对强化换热特性影响
进水流量分别为0.4、0.6、0.8、1、1.2 m3/h的PCM平均液化率曲线如图10所示。从整体趋势来看,两组翅片间距模型在不同流量下呈现出的液化率变化规律与0.6 m3/h,55 ℃工况下一致。因为两组翅片间距模型内部介质导热性能不同,所以不同流量对两组模型影响程度不同,在0.4、0.8、1.2 m3/h工况下,翅片间距为2λ比3λ模型完全熔化时间分别缩短了13.69%、17.61%、17.42%。分别来看,在前30 min内两组模型的液化率曲线是几乎分别重合的,说明流量的加大对熔化初期几乎没有影响,在30 min后随流量增加液化率曲线的斜率略微加大,表明传热流体流量增加熔化过程加快,但增幅较缓,分别在120 min和180 min左右进入缓慢熔化区,进水流量为1.2 m3/h时,与0.4 m3/h 工况相比,翅片间距为2λ和3λ模型的完全熔化时间分别缩短11.54%和8.17%,且两组模型在流量为1.2 m3/h与1 m3/h时,熔化速率变化较小,说明进水流量对换热情况的影响存在阈值。
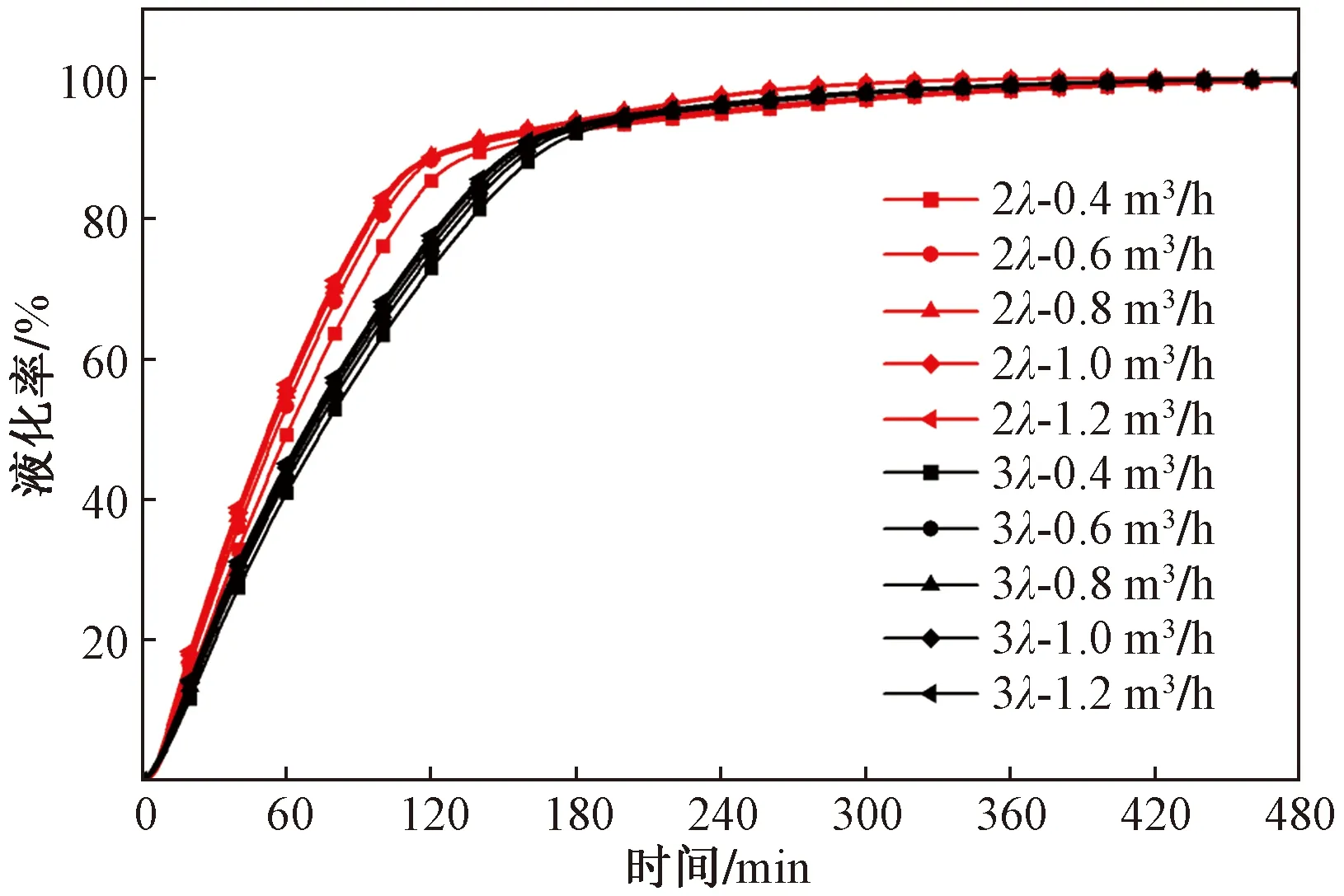
图10 不同进水流量PCM液化率曲线对比Fig.10 Comparison of PCM liquid phase volume fraction variation curve under different inlet flows
图11为不同进水流量下两组模型的储热量对比,整体而言,8 h仿真实验内随进水流量增大,翅片间距为3λ模型比2λ模型的储热量依次增加4.06%、7.05%、9.04%、10.77%、11.78%;分别来看,与0.4 m3/h工况相比,增大流量后翅片间距为2λ模型储热量分别增加4.46%、6.08%、7.41%、8.10%;3λ模型增加7.81%、11.56%、14.77%、16.59%,增长率减小。由于相同进水温度下PCM所能达到温度一致,以液态显热方式储存的热量相同,故同模型所能达到的总储热量是一定的,且增加流量会耗费更大泵功,因此流量的选取需要综合考虑。
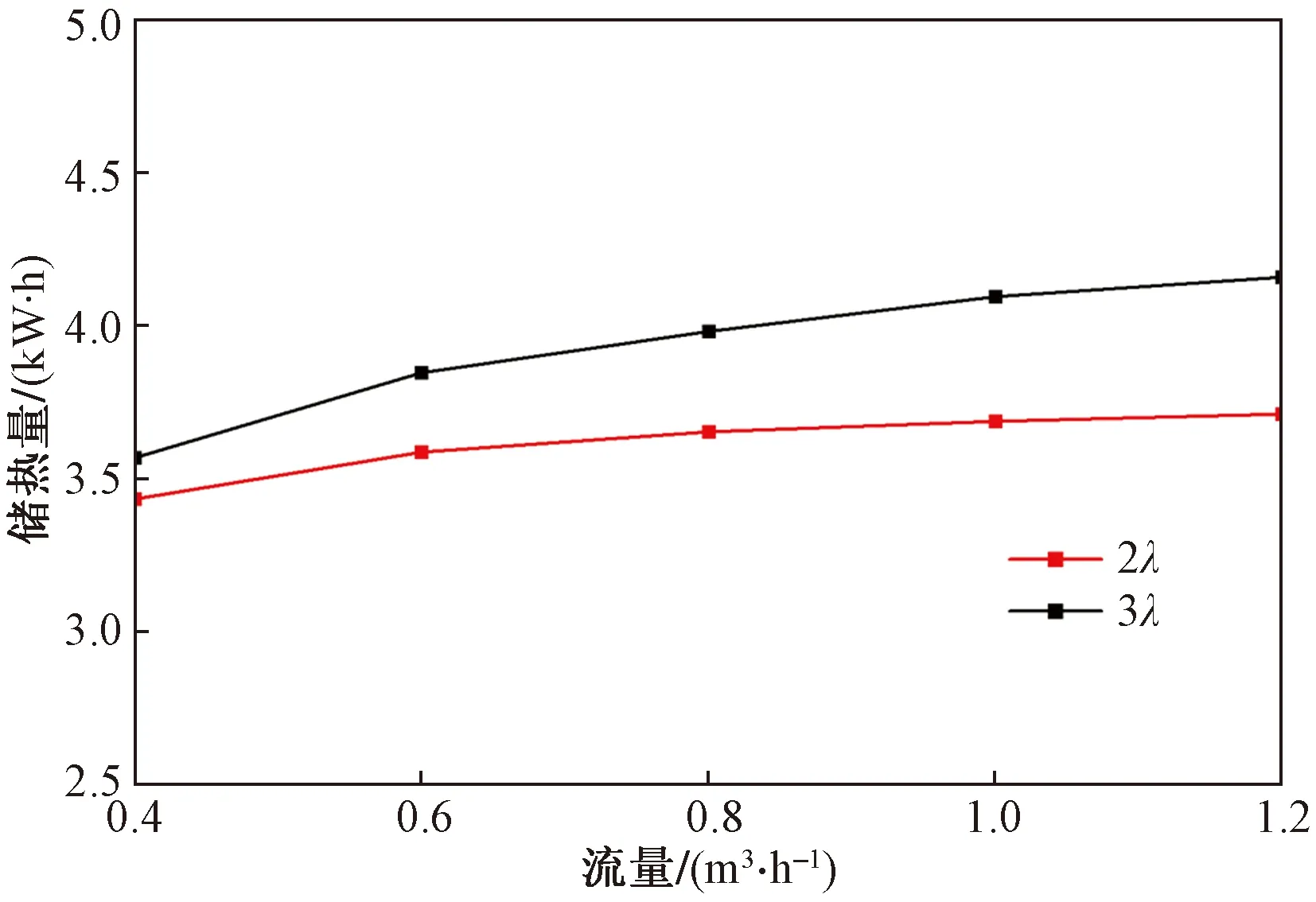
图11 不同进水流量储热量对比Fig.11 Comparison of heat storage under different inlet flows
2.4 实验结果
为验证数值计算模型的准确性,选取了翅片间距为2λ和3λ的相变储热单元搭建了如图12(a)所示的空气源热泵-相变储热实验系统。为与数值模拟结果相对比并得到更加准确的数据,在实际实验中共布置11根以铂电阻PT1000 温度传感器为探头的热电偶,如图12(b)所示,除与计算模型中位置一致的热电偶(T1~T7)外,还在翅片的中间位置、端部位置(T8,T9)以及保温层的内外侧(T10,T11)各设置了一根热电偶。
以进水温度为60 ℃,进水流量为0.6 m3/h的工况储热8 h,每组工况重复3次实验,从实验结果中各选取一组温度与仿真温度进行对比。
如图13所示,可见实验与仿真特征点温度变化趋势总体一致,采用式(16)分别计算两模型的均方根误差,公式为
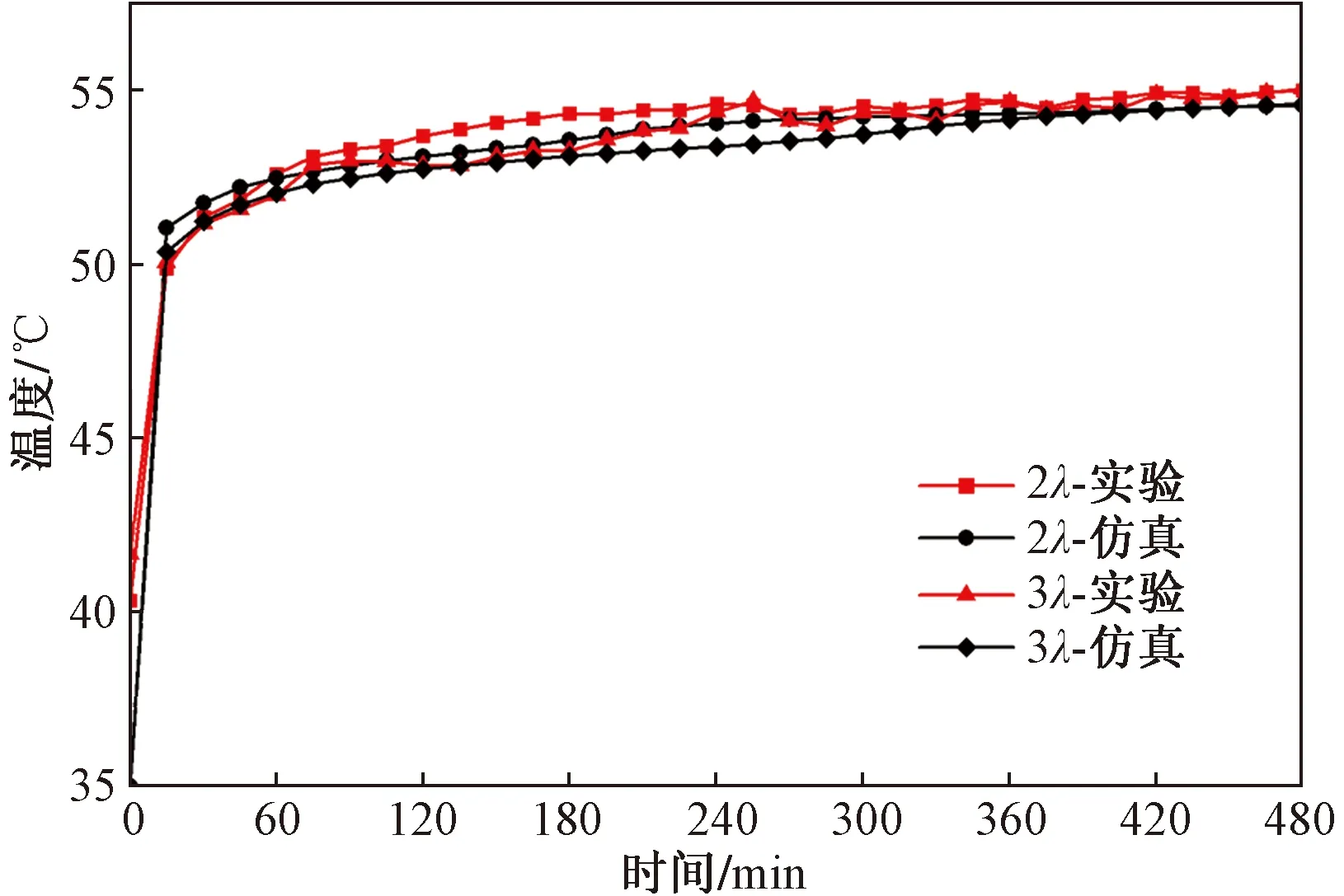
图13 仿真与实验特征点温升过程对比Fig.13 Comparison of simulation and experimental temperature rise processes at feature points
(16)
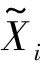
翅片间距为2λ和3λ模型的均方根误差分别为5.1%和3.3%。
换热功率对比如图14所示,实验与仿真计算结果趋势一致,两组翅片模型在熔化初期的换热功率分别达到了15 kJ/s和14 kJ/s,验证了数值模拟实验的准确性。

图14 仿真与实验换热功率对比Fig.14 Comparison of heat transfer power between simulation and experiment
3 结论
针对不同翅片间距模型的强化换热效果及不同进水温度、流量对其储热特性的影响规律进行研究,并通过实验验证了数值模拟模型的准确性。结果定量地反映出储热单元基于实际工况的工作特性,可得出以下结论。
(1)减小翅片间距增加接触面积,换热系数增加,强化换热效果明显,缩短熔化时间, 翅片间距为λ比4λ模型熔化时间缩短了79.47%,储热量减少13.31%。
(2)随进水温度升高,增加HTF与PCM的温差,提升换热系数,相变材料完全熔化时间大幅缩短,分别缩短了64.45%和65.77%;储热量分别增加17.27%和19.35%。增大进水流量后,换热速率增加,完全熔化时间分别缩短11.54%和8.17%, 进水流量为1.2 m3/h时,对两组模型储热速率提升不明显。
(3)减小翅片间距储热时间缩短,同时储热量降低,储热单元成本显著提高,因此储热时间充裕的情况下,可以考虑适当放宽翅片间距以降低换热器的成本。
对不同翅片间距下储热时间、储热量定量化研究,为项目提供理论和实验依据。通过对翅片间距的优化设计,提高换热效率,可促进相变储热装置在供暖方面的应用,解决可再生能源消纳。
