基于Isight的动力电池液冷板流量分配一致性优化分析

刘志恩，裴书卿，张振文，范蓉蓉，卢炽华

(1.武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉 430070；2.先进能源科学与技术广东省实验室佛山分中心，广东佛山 528225；3.湖北雷迪特冷却系统股份有限公司，湖北武汉 430058)

随着全世界资源危机以及环境污染的加重，锂电池电动汽车低污染、零排放的特点使其成为替代现有传统汽车的重要选择[1]。锂电池具有高比能量、低自放电率等优点，但该电池的循环寿命和安全性在很大程度上取决于电池实际工作温度。在急加速工况下，锂电池大电流放电产热功率较小电流工况大得多，此时电池容易发生安全隐患[2]，因此合理有效的电池冷却方法至关重要。

目前针对大功率产热电池进行冷却的主流方法是液冷，液冷分为直接和间接接触式两种，鉴于直接接触式为浸泡式，不利于后期的维护，所以目前研究和使用较多的是间接接触式。锂离子电池最适宜的工作温度范围为25～40 ℃，电池模组之间的最大温差应小于5 ℃以保证电池的最佳性能和寿命[3]，现有研究主要是通过改进流道结构达到提高液冷板对电池模组的冷却效果的目的，却鲜有针对减小模组之间温差的。本文旨在研究流道结构对单入口多支路的液冷板流量分配一致性问题，并提出一套适用于实际液冷板产品的优化方法对现有液冷板进行优化。

1 模型建立与网格无关性

1.1 三维模型建立

本文建立了一种单一进出口的四支流液冷板简化模型，研究各个支路入口的宽度、倾斜角度对液冷板流量分配一致性的影响，模型简化后保证与实际并无明显差异。液冷板流道入口主流道宽24 mm，出口主流道宽22 mm，冷管厚度4 mm、间距12.7 mm，如图1 所示。

液冷板安装在电池模组底部，通过间接接触式对电池进行散热。冷却介质从进水口进入，流经四个支路的蛇形流道带走热量，再经由出口汇流，从出水口统一排出。

1.2 流体计算模型建立

1.2.1 流体计算模型选取

本文基于STAR CCM+进行计算流体动力学(CFD)仿真，在进行仿真计算前需要考虑流体在液冷板中的流动状态，以此来界定计算模型。

液体的流动状态分为层流和湍流，当液体的雷诺数小于2 300 时，流体受粘性作用控制，使流体因受扰动所引起的紊动衰减，流动保持为层流。随着雷诺数的增大，粘性作用减弱，惯性对紊动作用的激励增强，到雷诺数大于4 000 时，流动受惯性作用控制，流动转变为紊流[4]。雷诺数的计算公式为：

式中：ρ为流体密度；v为流场特征速度；L为流场特征长度；μ为流体粘度。

冷却介质采用50%乙二醇溶液，冷却介质工作时的温度为25 ℃，流量为10 L/min，其物性参数如表1 所示[5]。

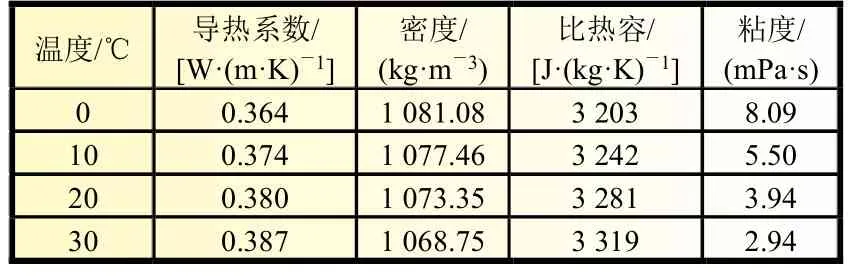
表1 50%乙二醇溶液物性参数

根据上述条件进行计算后，冷却液流动过程中的雷诺数大于4 000，流动方式为湍流，因此采用标准的k-ε湍流模型，模型控制方程为：

式中：k为湍动能；ε为湍动能耗散率动能的生成率；σk为湍动能对应的普朗特系数；σε为湍能耗散率对应的普朗特系数。

1.2.2 边界条件

在STAR CCM+的仿真过程中，设定放置于液冷板上方的电池模组为热源，整块电池各处体积均匀产热，且忽略电池模组与空气的对流换热，只与下方液冷板进行传导换热。电池产热功率稳定，不随时间产生变化。

液冷板进水口边界类型设定为质量流量入口，质量流量为0.054 8 kg/s，湍流强度为0.03，湍流特征长度0.5 mm，冷却液初始温度为25 ℃。出水口边界类型设定为压力出口，出口压力设定为0 Pa。导热垫厚度1 mm，导热系数为3 W/(m·K)，导热垫密度为2 400 kg/m3。电芯密度为2 546 kg/m3，电池模组产热比功率稳定在300 W/m3，模组的导热系数各项异性，沿X、Z轴方向的导热系数为13.2 W/(m·K)，沿Y轴方向的导热系数为0.73 W/(m·K)。

1.3 网格无关性分析

对图1所示液冷板流体域三维模型进行网格划分过程中，采用了多面体网格以及边界层网格生成器，网格基本尺寸为5 mm，最小表面网格尺寸为0.5 mm，表面网格增长率为1.3，边界层层数为3，边界层增长率为1.2，边界层厚度为1.28 mm。

在保证仿真结果精准度的前提下，需要通过降低模型的网格划分数量来保证计算效率。图2 为网格无关性验证的结果。结果表明，当网格数量大于53 万时，进出口间的压降误差小于1%。

2 仿真结果与分析

2.1 等入口直径液冷板流量分配

保持四个蛇形流道[6]支流入口宽度为10 mm，各个支流入口与主流道保持垂直，其余变量保持不变，且入口宽度与出口宽度变化保持一致，便于减少几何结构的变量数。仿真过程中建立四个监视面(X=0 mm，Y=70 mm，Z=0 mm)，监测流出各个模组的实际流量。

图3 为四个支流入口宽度保持一致时的质量流量分配情况，入口宽度分别为5、10、15 mm。

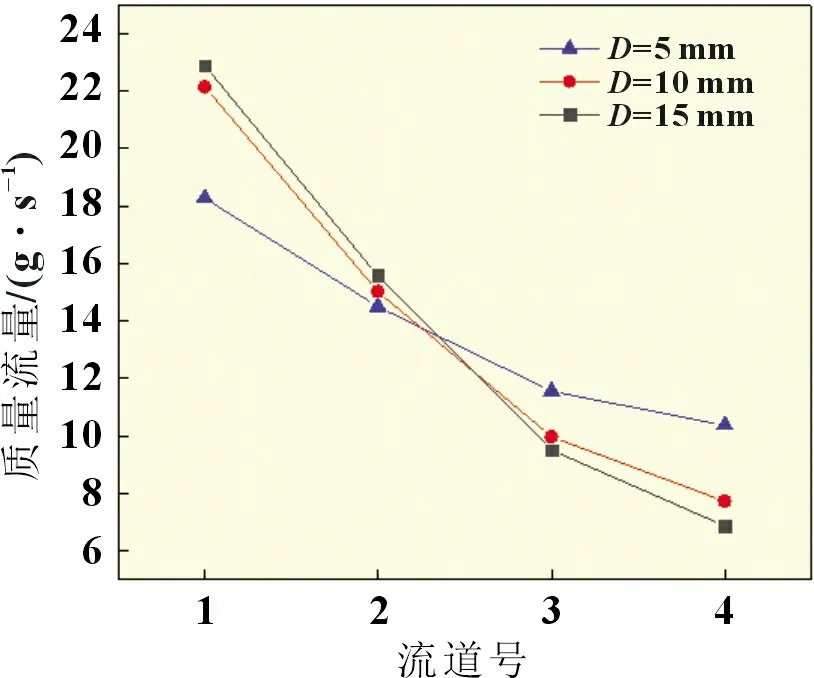
图3 等直径流道在不同直径下的流量分配

由图3 可知，在D=10 mm 的等直径液冷板中，随着液冷板流道号的增加，各个模组支流的流体流速和流线的疏密程度在逐渐下降，冷却介质流经模组换热后进入汇流流道。此外，随着入口直径的增大，分配到1 号支流的流量在逐渐增多，3 号和4 号支流的流量明显下降，液冷板整板的流量分配均匀性较差。

2.2 基于Isight DOE的自动运算方法

Isight 是一个仿真分析流程自动化和多学科多目标优化工具，提供与多种主流计算机辅助工程(CAE)分析工具的专用接口，利用Isight 可以将CATIA 和STAR CCM+快速集成，通过改变CATIA 中的宏文件和STAR CCM+中的脚本文件以实现三维模型以及边界条件的自动更新。集成过程中需要给定模型的优化变量个数以及每个变量的水平数，本文主要针对图1 模型进行流量分配规律总结和结构优化，使用Isight实验设计(DOE)中的全因子方法进行计算，该方法将所有变量进行全排列组合，该方法的优势就在于获取信息的全面性[7]。

2.2.1 流道入口宽度对流量分配影响

本文分别考虑了入口宽度、支流角度对流量分配的影响，在本节中保持支流入口角度90°不变，通过改变四个支流的入口宽度来观察该变量对流量分配的影响程度。

初设入口宽度D1～D4的变化范围为0～10 mm，各个变量的水平数为5，变化步长是2 mm，共计625 组计算方案。

图4 为Isight DOE 全因子计算后作出的帕雷托(Pareto)图，蓝色数值条代表该变量起正影响，红色代表负影响。图4表征各个变量对目标的贡献比例大小，变量的影响程度与数值大小成正比。

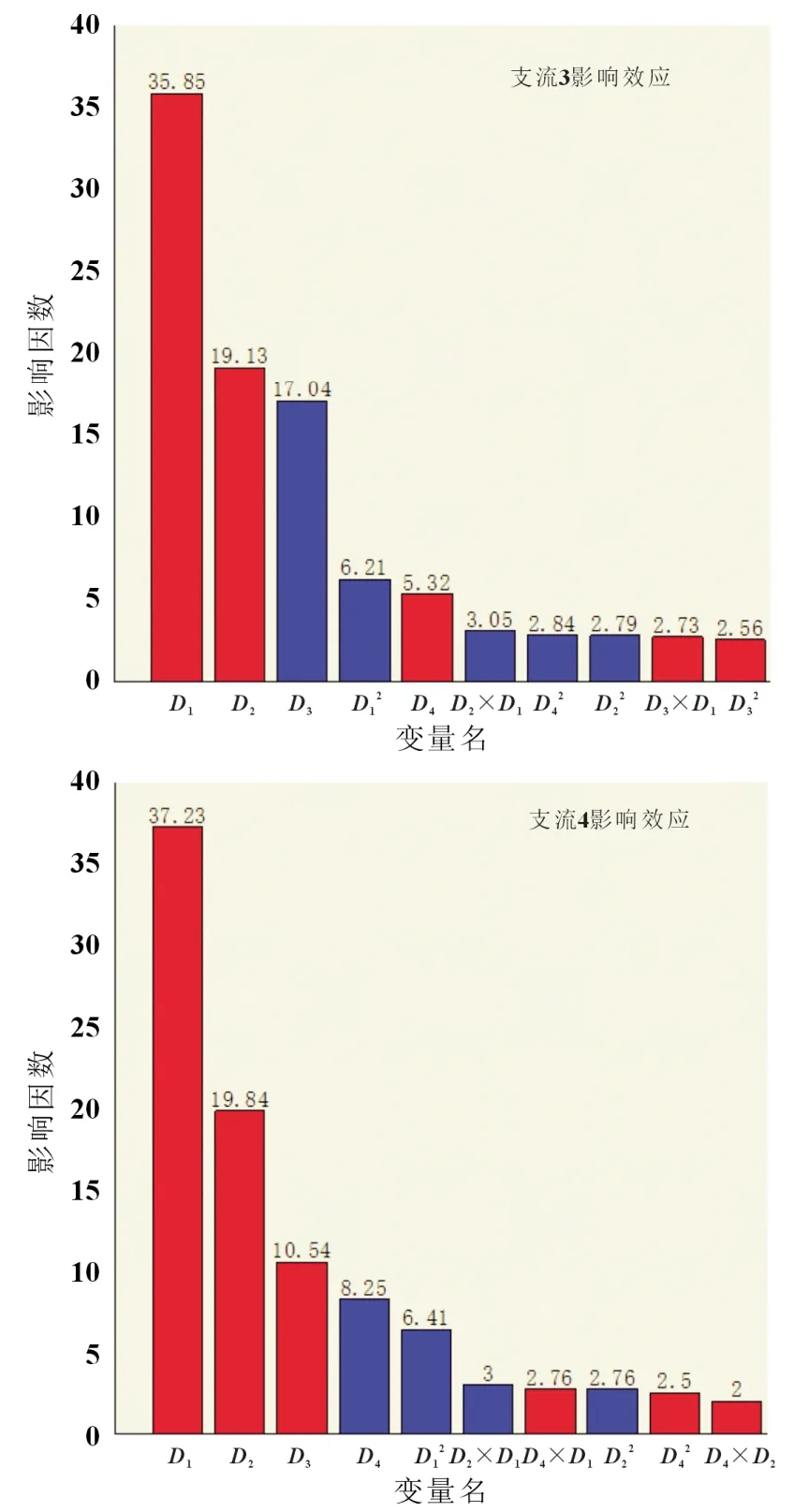
图4 流道直径对流量分配影响的Pareto 图

由图4 可知，对1 号支流流量分配影响最大的是1 号支流自身的流道宽度D1，其次是2 号支流宽度D2，但D1的影响程度高达72.91，占主要地位。

为了更加直观地评价D1和D2对1 号支流流量分配的影响，计算图3 中三条折线的D1为1～5 mm 的斜率，再取三个斜率的平均值，如式(4)～(5)所示：

由式(5)可得D1～D4中对四个支流流量分配影响较为明显的变量的平均变化率，如表2 所示。

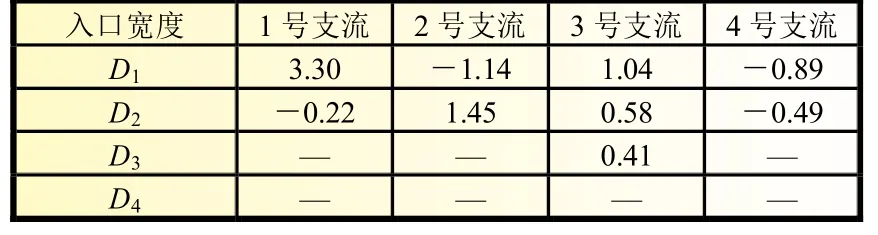
表2 支流入口宽度对流量分配的平均变化率 g/mm

式中：t=1～4。

综上所述，针对上述四支流液冷板在仅考虑支流流道宽度时，对流量分配起决定性影响的是D1和D2两个变量，D3和D4所产生的影响有限，所以在进行流道宽度设定时，应该重点考虑D1和D2的合理性。

2.2.2 流道倾斜角度对流量分配影响

限制1～4 号支流入口宽度为10 mm，改变支流入口的倾斜角度，考虑到流道倾斜角度过大的时候冷却液进入冷板后会产生较为明显的一侧偏移，导致冷却液的分布均匀程度下降，倾斜角度变化范围为80°～100°，变化步长为10°，水平数为3，分别为80°、90°、100°，计算方案总数为81 组。

图5 为流道倾斜角度对流量分配影响的Pareto 图，随着支流入口倾斜角度a的改变，对1 号支流流量分配影响最为明显的是1 号支流入口流道的倾斜角度a1，且影响为正，其次是2 号支流入口流道的倾斜角度a2，a2越大，则其流量越小，a3和a4的影响较小，可以忽略。

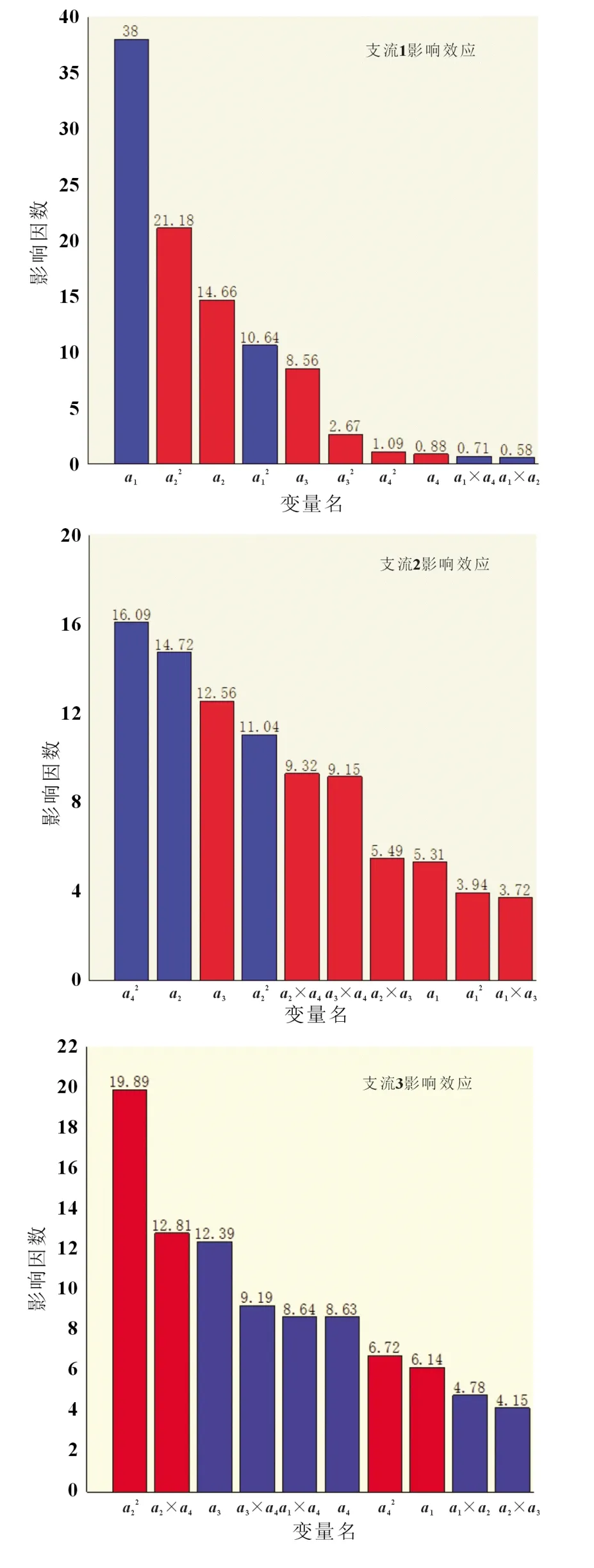
按照2.2.1 所示计算支流宽度对支流流量变化率的方式计算角度对不同支流流量变化率的影响，计算结果如表3 所示。

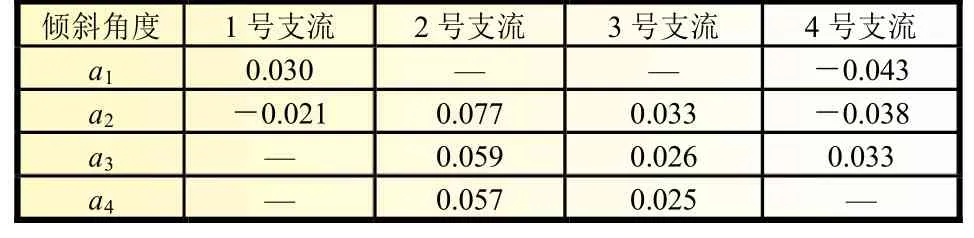
表3 支流倾斜角度对流量分配的平均变化率 g/rad

综上所述，角度变化对各个支流的流量分配的影响远小于各支流入口宽度对支流流量分配的影响。

2.3 液冷板优化方案

由2.2 节可知，液冷板的支流入口宽度比倾斜角度影响更大，D1和D2的影响最为显著。由2.1 节可知，当支流的入口宽度相等时，冷却液的流量分配会随着支流号的增加逐渐下降，所以针对液冷板的优化方案应该重点集中在对D1和D2的调控上，减小D1和D2，增大D3和D4。

重设DOE 中支流宽度的变化范围，D1和D2变为1～5 mm，D3变为5～10 mm，D4变为10～15 mm。D1和D2水平数都为5，变化步长为1 mm，D3和D4的水平数都为3，变化步长为2.5 mm，由此共得到225 组方案。

如若在上述参数变量范畴内没有获得流量一致性较好的方案，可以继续扩大D3和D4的变化范围；如若在上述方案中获得了流量分配一致性较好的方案时，可以继续缩小和细化参数的变化范围和参数的步长，进一步提高优化效果，优化流程如图6 所示。

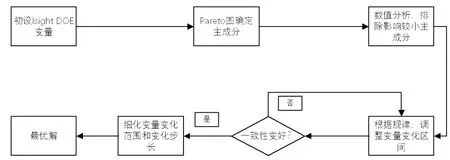
图6 基于Isight的迭代优化流程

各支路流量分配一致性使用标准差的计算方法来进行综合评价，该方法更加客观准确，其计算方法如式(6)所示：式中：σ为质量流量的标准差；Xi为各个支路实际分配的质量流量，i为流道号；μ为四个支路所获质量流量分配的平均值；N为总的支路数量。

由上述步骤最终获得的优化方案为D1=3 mm，D2=5 mm，D3=7 mm，D4=15 mm，优化前后的各支路流量分配如图7 所示。

图7 优化前后支路流量分配对比图

2.4 流固耦合传热仿真结果

根据优化结果，更改三维数模，并将液冷板、导热垫片、模组三者进行装配，导入STAR CCM+中进行流固耦合传热仿真，对液冷板上、下板采用多面体网格，对流体域采用带边界层的多面体网格。因为导热垫片仅有1 mm 厚度，较为单薄，所以采用薄壁层网格，模组自身比较规则，采用切割体网格。

根据1.2.2 节的边界条件设置仿真，并对1～4 号模组顶面进行了平均表面温度、最大表面温度和最小表面温度的监测，计算1～4 号模组顶面最大温度和最小温度之差，评价液冷板中支流流量分配一致性对模组顶面温差的影响，仿真结果如图8 所示。

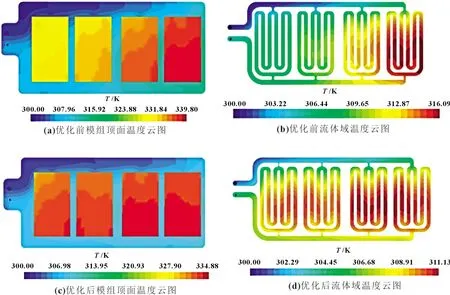
图8 优化前后温度云图

由图8 可以明显发现优化前后四个模组顶面温差的改善，1～4 号模组顶面平均温度为θj，j为模组号。表4 给出了优化前后流量分配一致性的标准差、1～4 号模组顶面平均温度以及最大温差。

表4 优化前后指标对比 ℃

2.5 实验验证

将上述优化结构冲压成型，放入实际实验台架中进行测试，该测试台架可以保证一定温度的冷却液稳定输入，经由仪表读取整板的流阻和压降以及电池顶面温度。

实验测得的电池顶面温度一致性与仿真值基本一致，实验与仿真之间的差距源于仿真过程中简化了实验所用液冷板部分圆角和尖锐结构。此外，置于电池顶部用于监测温度的传感器所监测的范围并不是整个电池顶面，而仿真结果是电池顶面温度平均值，实验与仿真结果对比如图9 所示。

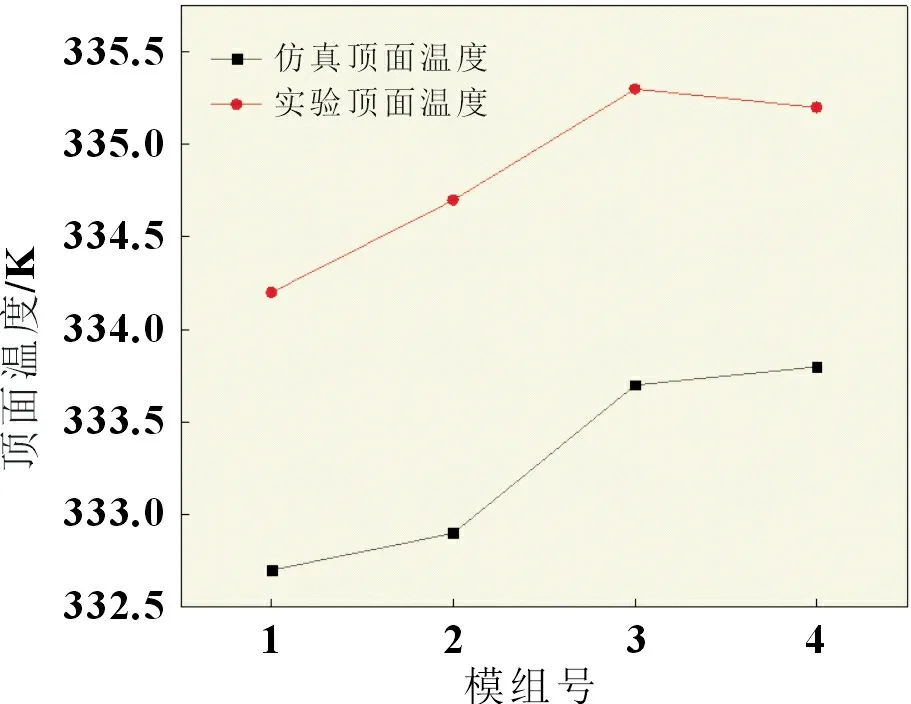
图9 仿真和实验数据对比

3 结论

本文研究了液冷板中支流入口宽度和倾斜角度对流量分配的影响，以及在电池模组稳定功率放热的条件下，液冷板中各支流流量分配一致性优劣对模组顶面温度差的影响。结果表明，液冷板的支流宽度对支流流量分配的影响较为明显，尤其是D1和D2；支流的倾斜角度存在一定的影响，但并不是主要的影响因素，由此确定了基于Isight DOE 的迭代优化方法，最后以各个支流流量分配的标准差来评价各个支路流量分配一致性的好坏，并将最终得到的优化结构代入STAR CCM+进行流固耦合传热仿真。观察对比未优化的液冷板和优化后的液冷板传热仿真结果，发现优化后的模组顶面最大温差较未经优化的小6.38 ℃。将该优化结构在实验台架上进行了实际工况的实验，发现实际效果基本符合仿真结果，电池的顶面温差较未优化结构降低了很多，说明了该优化方法的可行性。