在解决问题的过程中生成数学概念——《倍的认识》教学实践与反思

文| 陈 敏 王雪晴

【教学背景】

“倍”是小学数学中的一个重要概念。通常的处理是在规定“把A 看成1 份”的基础上，引导学生理解“B 有这样的几份，B 就是A的几倍”（如图1）。这样虽然把“倍”的意思说得清晰、利落，但为什么要把A 看成1 份，又为什么按这样1 份1 份去度量B，亦即，为什么要对A、B 做乘法性的比较缺少缘由。

图1 人教版《数学》三年级上册第50 页

图2

图3

图4

实际上，对两个数量是进行加法性比较还是进行乘法性比较“既不是假设的，也不是规定的，而是根据个人想要知道什么、需要解决什么来建构的”，即，这是一种“刻意的关系”。若创设问题情境，引导学生经历刻意的关系的建构和交流过程，将有益于增进学生的模型意识，发展他们的量化推理能力。

基于上述思考，本课尝试引入喂鱼及搭积木的日常情境，鼓励学生探讨其中的数量关系，促成“倍”概念的发生和发展，建构乘法模型。经实践，效果良好。

【教学对象】

二年级学生，已经学习了2～4的乘法口诀以及对应的除法计算。

【教学内容】

一、情境导入，引发比较

师：这个周末，老师去花鸟城买了两条小鱼。看，鱼哥哥和鱼弟弟朝我们游过来了！你能辨认出谁是哥哥？谁是弟弟吗？

师：老师打算每天给鱼弟弟喂2 粒鱼食。你觉得给鱼哥哥喂几粒合适呢？

生1：3 粒。因为鱼哥哥长得比鱼弟弟大，所以吃得肯定也多一点。

生2：4 粒。因为哥哥看起来有2 个弟弟那么大，2+2=4（粒）。

【设计意图：题材取自Kamii等（1996）使用的一道乘法思维检测题。以学生熟悉的喂鱼情境引入，激发学习兴趣，探明学习起点：生1 采用定性分析，知道要“吃得多一点”，选择算法“2+1=3”，体现为加法思维水平。生2 则基于图像，定量判断出“哥哥有2 个弟弟那么大”，初具乘法思维水平。】

二、深入讨论，理解倍比

1.比较身长，确定鱼食

师：两位同学都认为哥哥比弟弟“长得大”，所以要“吃得多”。那到底怎么把握哥哥和弟弟的大小，又怎样根据大小比较合理地喂食呢？

师：我们先来说说，哥哥和弟弟的大小可以怎么比较？

生1：我觉得可以比较它们的长短。

生2：我觉得也可以比较它们的轻重。

（板书：身长、体重）

师：请一位同学来比比身长。

生1 操作课件呈现：

生2：哥哥比弟弟长。

生3：看起来鱼哥哥的身长是鱼弟弟的2 倍。我可以上来再量量看吗？

（生3 操作，集体观察：正好量了2 次）

生3：鱼哥哥的身长就是鱼弟弟的2 倍。

生4：也可以说，鱼弟弟的身长是鱼哥哥的一半。

师：很好，用上了我们昨天刚刚学习的 “2 倍” 和 “一半”。

【设计意图：学生已具有2 倍和一半的比较及表达经验。前一课中，特别安排借助复印水彩点的活动，学习了2 倍和一半关系（如图5）。鱼兄弟身长2 倍（一半）关系的视觉效果比较明显。为完成合理喂食的任务，需要对鱼的身长进行更为精确的比较。以上多个因素叠加，学生主动对鱼身长进行了乘法性比较。】

图5 自编的“2 倍和一半”课时方案

图6

师：身长的关系清楚了，按照这样的关系，你们觉得给哥哥喂几粒鱼食比较合适呢？

生1：鱼哥哥的身长是鱼弟弟的2 倍，食量也是鱼弟弟的2 倍。

生2：弟弟吃2 粒，哥哥身长是它的2 倍，就是2 个2 粒，2+2=4（粒）。

生3：也可以用乘法计算：2×2=4（粒）。

师：如果鱼哥哥的食量是鱼弟弟的2 倍，也就是说——把鱼弟弟吃的2 粒看成1 份（贴1 条线段，并板书：1 份——2 粒），鱼哥哥要吃这样的2 份（贴2 条线段，并板书：2 份——？粒），鱼哥哥要吃4 粒。［板书：2×2=4（粒）］

【设计意图：在学生回答的基础上，初步梳理出倍比的分析框架：先确定1 份量，再确定有这样的几份是多少。线段图、对应式和乘法算式互相生成，互为参照，实现对“倍”概念的多元表征：线段图是几何直观；对应式揭示数量结构；最后凝聚为乘法算式。】

2.比较体重，确定鱼食

师：有同学说也可以按体重喂，体重是怎样的关系呢？

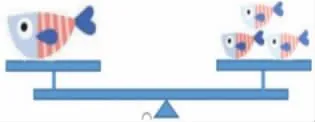
生1：1 条鱼哥哥等于3 条鱼弟弟那么重。

师：可以试试用“倍”来说吗？谁来试试？

生2：鱼哥哥的体重是3 倍。

师：怎样的3 倍？

生3：鱼哥哥的体重是鱼弟弟的3 倍。

师：为什么认为“鱼哥哥的体重是鱼弟弟的3 倍”呢？

生4：可以学习2 倍的方法。1条鱼弟弟的体重是1 份，3 条就是3 份，鱼哥哥等于这样的3 份，所以鱼哥哥的体重是鱼弟弟的3 倍。

生5：把鱼弟弟的体重看作1份，鱼哥哥的体重有这样的3 份，鱼哥哥的体重就是鱼弟弟的3 倍。

强调：我们一起像生5 这样说一说——把（ ）看成一份，（ ）有这样的（ ）份，（ ）是（ ）的（ ）倍。

师：那按照这样的体重关系，给鱼哥哥喂几粒鱼食比较合适？

生1：给鱼哥哥喂这样的3倍：2×3=6（粒）。

生2：鱼弟弟吃1 份是2 粒鱼食，鱼哥哥吃这样的3 份，就是2×3=6（粒）。

【设计意图：借助天平直观，激励学生将“2 倍”的分析经验迁移到“3 倍”的情境中。强化倍比的分析框架、语言表述和数学表示。】

三、推广举例，丰富理解

师：好，我们给鱼哥哥喂上鱼食。按2 倍的话，要喂——4 粒（课件演示）；按3 倍的话，要喂——6粒（课件演示再添2 粒）。

生1：我感觉6 粒太多了，小鱼要撑坏的。4 粒比较合适。

师：你提醒得好。我们按这样的关系来计算鱼食，其实只是一种设想。到底怎样喂鱼，可能我们还得去请教一下养鱼专家。那同学们，你们在生活中遇到过像这样“倍”的问题吗？

生1：周末我有2 个培训班，我姐姐有4 个培训班，姐姐的培训班个数是我的2 倍。

生2：有一天，我想吃2 个冰淇淋，弟弟想吃6 个冰淇淋，弟弟想吃的是我的3 倍。

师：怎么知道是3 倍呢？

生2：2 个是1 份，6 个有这样的3 份，6 个是2 个的3 倍。

师：你分析得真清楚。不过冰淇吃太多，对身体可不好，你可以劝劝弟弟。还有想说的同学吗？

生3：我们有100 米和50 米两种测试，100 米的长度是50 米的2 倍。

师：预测一下跑100 米和跑50米用的时间，可能是什么关系？

生4：可能也是2 倍。

生5：要同一个人跑，跑100米花的时间是跑50 米的2 倍。

生6：也不一定，可能路长了以后，会跑得慢下来。

师：想得很周到！你们想强调的是跑的速度不变，跑100 米花的时间是跑50 米的2 倍。对吗？

生7：我知道生活中的倍数不一定正好是2 倍、3 倍，新闻里有时也说1.5 倍，1.2 倍。

生8：中国人口大约是14 亿，美国人口大约是3 亿，我们的人口比美国的4 倍还要多。

师：这里的一份数是？怎么知道是4 倍还要多？

生：3 亿人。3×4=12 亿，小于14 亿……

师：一份也可以有3 亿那么多，好大的一份呀！

生8：我把半个月饼看成1份，8 个月饼是半个月饼的……8个半个是……8 个是半个的……

师：自己有点说晕了。我们帮他理一理。（在黑板上画半个圆和8 个圆）1 份是——半个，8 个可以分为这样的（用手指引导学生观察和计数）——16 份。现在可以自信地说出来了吗？

生8：8 个是半个的16 倍。

师：掌声送给他。一份可以很大，也可以很小，同学们真棒！

师：同学们，你们举了这么多“倍”的例子，它们有什么共同的地方吗？

生9：倍就是两个数比，其中1 个看成1 份，另一个看看有这样的几份，就是它的几倍。

生10：1 份可大可小，看我们自己选谁做1 份。

生11：1 份大了，倍数就小；1份小了，倍数就大。

生12：一半也是倍，不到1 倍。

【设计意图：引导学生通过类比、联想其他生活经验，进一步理解“倍”的意义。在举例过程中，教师有针对地进行追问，巩固倍比的基本分析框架，适当增加推理的复杂性。同时，教师经由学生的回答诊断学生的概念掌握情况并概括和凸显倍比的本质。】

四、综合运用，发展推理

师：我们来看另外一项同学喜欢的活动——搭积木。

师：请你打开作业纸，先自己静静地写一写好吗？

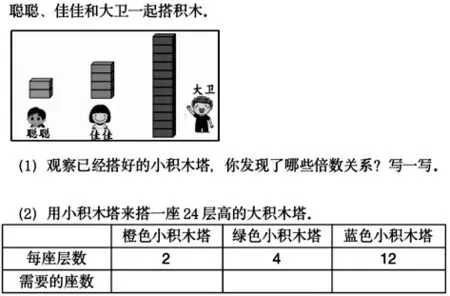
生1：我发现，绿积木的高度是橙积木的2 倍。蓝积木的高度是橙积木的6 倍。

师：对吗？也是这样写的同学举手。关于这个发现，你们有什么想说的吗？

生2：积木越高，比出来的倍数也越高。

生3：都和橙积木比，蓝积木高，比出来的倍数也大；绿积木矮，比出来的倍数就小。

师：意思是，一份量不变，比较量越大，比出来的倍数也越大。是吗？那如果比较量不变，倍数会变吗？

生4：会变的。比如说，我比的都是蓝积木。如果和橙积木比，蓝积木是橙积木的6 倍；但是和绿积木比，蓝积木只是绿积木的3 倍。

师：一份量变了，比较的结果也会变。

生5：一份量越大，比出来的倍数反而小了。

【设计意图：直观比较，检查学生基础目标的达成。对比较结论进行比较，渗透一份量、比较量和倍数三者之间的函数关系。】

师：要搭一座24 层的大积木塔，要用几座小积木塔？你们算出来分别是多少呢？

生1：蓝积木塔最高，算起来最快：12+12=24，用2 座就够了。24÷4=6（座），绿积木塔的话，要用6 座。

师：橙色的呢？

生1：橙积木塔是24÷2，我们还没有学过。

生2：先算12÷2=6，6 座橙色塔搭成1 座蓝色塔。再用6×2=12，2 座蓝色塔=12 座橙色塔。

师：大家听懂了吗？

生3：我想的和生2 有点像。因为绿积木的高度是橙积木的2倍，那么需要绿积木的座数应该是橙积木的一半，绿积木要：24÷4=6（座），橙积木要：6×2=12（座）。

师：生3 说到好几组倍数关系，我们来捋一捋。绿积木的高度是橙积木的2 倍，有问题吗？所以绿积木的座数只要橙积木的一半，同意吗？为什么？

生4：一份量越大，倍数越小。把绿积木当成比较量，这个一份量大，比出来倍数小；橙积木这个一份量小，比出来倍数多。

生5：1 块绿积木=2 块橙积木，6 块绿积木=12 块橙积木。大家都乘6 倍。

生6：其实就是想，越矮的积木，要用的块数就越多。

师：大家真是太厉害了！从会比较倍数，到会用倍数推算，又上了一层楼。

【设计意图：进一步挑战学生的推理。生1 使用大塔层数÷小塔层数求取需要的小塔座数，依赖于数值计算，可诊断为加法思维水平，在橙色塔问题上遇到了困难；生2 对此做了优化和推进，其推理过程可表达为24÷2=（12+12）÷2=12÷2×2，具备一定的乘法思维；生3 采用反比推理，基于小塔之间的高度关系推断小塔座数之间的关系，简洁高效，体现出较高的乘法思维水平。促进不同水平学生之间的交流，在将他人思考与本人思考进行比较与联系的过程中，内化、提高。】

【反思】

对于一些重要的数学概念、关系，教师往往把备课的重点放在怎样帮助学生理解和掌握这些概念、关系上，却疏忽了如何引发学生的学习动机，即，为什么要学习这个内容？如倍的认识，有多次听课的经历表明，当课堂上呈现兔子和萝卜图（图1）时，二、三年级的学生更倾向于从多少的角度而非倍数关系来提出分析。“倍”变成了教师的选择，当堂的规定。

《义务教育数学课程标准（2022 年版）》提出要“注重发挥情境设计与问题提出对学生主动参与教学活动的促进作用，使学生在活动中逐步发展核心素养”。Savard 也建议 “任务的设计需要镶嵌于社会文化情境中，从而学生能将自己看作是积极的代理人”。在本课中，我们没有使用以往课堂中常见的、直接要求比较物品倍数关系的任务，而采用喂鱼、搭积木等情境，先激活学生“大鱼多吃，小鱼少吃”“高积木用得少，矮积木用得多”之类的日常经验，再推动他们逐渐量化，主动从“倍”的角度分析情境，建构数量关系。我们期望经由这样的学习过程，可以帮助学生体会到数学中有很多概念和关系都是人们出于分析和解决问题的需要，主动建构和发明的，而这些建构和发明的概念、法则能大大增进人们对现实世界的理解和把握。我们相信，如果学生经常有机会从自己熟悉的情境开始，自觉反思和加工自己的应对经验，逐步迭代成更为准确和高效的概念、法则，进而改善他们对数学学习的信念，同时，也能降低概念和法则的学习难度，增进学生的理解。

另外，需要提出，课堂上学生也讨论到 “6 粒太多了”“喂鱼不完全按照大小关系” 等等，这些评价恰恰体现了学生对任务真实性的感受，对数学模型的理解，是思维批判性的表现，有了进一步学习的可能。素养导向的课堂不正应该包容乃至追求这样的弹性吗！