莫让材料“暗示”僵化了学生的思维——以《三角形的面积》教学为例

文| 许燕萍 俞 军

在《义务教育数学课程标准（2022 年版）》中明确指出：数学教学应让学生经历独立的数学思维过程，理解数学基本概念和法则的发生和发展，探究自然现象或现实情境所蕴含的数学规律，经历数学“再发现”的过程，发展质疑问难的批判性思维，初步养成讲道理、有条理的思维品质，逐步形成理性精神。因此，在课堂教学中，我们必须合理选择学习材料，充分暴露学生的原生态思维，激发他们的思维广度，使其深入思考，集思广益，提出解决问题的多种策略，深刻体验知识产生的过程，让学生的学习真正发生。带着这种理念，笔者对《三角形的面积》一课教学进行了反复实践，现将磨课中的一些思考与各位同仁分享。

环节一：精选探究材料，暴露学生思维

课堂上教师提供不同的学习材料，学生的思考就会有不同的方向。如果像教材那样提供两个完全一样的三角形，学生可能就只会想到“倍拼法”，这样的安排给学生过多的暗示，局限了学生的思维。如果仅提供一个三角形，学生想到的可能就是画出示意图，此时，相比教材呈现的方法就更为丰富多样。

【教学片断1】

教师多媒体出示三类不同的三角形（如图1）。

图1

师：如果让你任选一类三角形来研究，你会选哪个？（学生齐答：直角三角形）

师：直角三角形的面积该怎么计算呢？把你的想法表示在图上，然后再算一算，请完成《学习单》的第一题。

（学生独立探究，教师关注学生探究的情况，了解学生的探究过程，并指导学生解释计算背后的思考过程）

教师巡视中有意选取三种转化方法投影反馈（如图2）。

师：这是三位同学的作品，你看得懂吗？请把你看懂的跟同桌交流一下。

师：我们一起来交流吧！谁先来说说？

生1：我看懂了第一种，他是用两个一样的直角三角形拼成长方形。

生2：三角形的面积是长方形面积的一半，所以可用16×10÷2来计算。

（教师根据学生的回答将这种方法贴到黑板上）

师：另外两种呢？谁能指着说一说？

生：第二种是剪掉一个三角形，把它拼到下面来，拼成一个长方形。

师：这一刀能随便剪吗？

生：不能，要剪在高的中间，这样才能拼成长方形。

师：现在谁会计算三角形的面积？

生：长方形的长是16，宽是10÷2，所以列式为10÷2×16。

师：一个三角形也能转化成长方形，真了不起!老师也将这种方法展示到黑板上。

生1：第三种跟第二种一样，都是剪掉三角形拼成长方形，只是第二种沿高的一半剪开，而这种是沿着底的一半剪开。

生2：我来补充算式：16÷2×10。

师：同学们真厉害！在研究直角三角形的时候都想到了转化成已经学过的长方形来计算。

这一环节，教师只提供《学习单》上的一个三角形，变教材主导材料为教学需求材料，为学生创设了探究的时空，能充分暴露学生的原生态思维。由于学生已有的知识经验和思考的角度不同，呈现的方法就多种多样。

环节二：紧扣数学本质，完善学生思维

直角三角形虽然有它的特殊性，但它的研究方法跟锐角三角形、钝角三角形乃至其他平面图形面积的研究是一样的，其数学本质都是转化的思想方法。教学中，可以让学生借鉴直角三角形的研究方法，自觉迁移到锐角三角形、钝角三角形的研究中，实现转化方法的多样化。

【教学片断2】

师：你们能带着刚才的研究经验再来探究探究锐角三角形和钝角三角形吗？

教师在巡视中有意识地选择三种典型方法，投影：

1.展示图3

图3

师：这种方法你能看明白吗？

生1：这两个三角形都是补了一个完全一样的三角形拼成平行四边形，也就是黑板上的第一种方法。

生2：三角形的面积都是拼完后平行四边形面积的一半。

2.展示图4

图4

师：这又是怎么想的？

生1：他是将上面的三角形旋转拼到下面，变成一个平行四边形。

生2：也就是黑板上第二种方法，沿着高的一半剪开。

师：算式中12÷2 是什么意思呢？

生1：是平行四边形的高，也就是原来三角形高的一半。

生2：我觉得还可以沿着底的一半剪开。

师：真会思考！底的一半剪开，拼成的是怎样的一个图形？在脑海中想想看。

3.展示图5

图5

师：有同学是这么想的，跟你想的一样吗？这种方法你有什么疑问吗？

生1：底的一半怎么找？

生2：对折。

生3：应该是左边底的一半剪开，右边底的一半也剪开，分别拼到上面。（请学生指一指）

师：你们真了不起！现在我们一起以动态的方式来回顾刚才的这几种转化过程。

（教师课件动态演示转化过程，图略）

师：你们很厉害！想到了这么多种转化方法。那么，现在请你观察黑板，你觉得三角形的面积可以怎么算？

生：（齐）底×高÷2。

教师根据学生回答，板书：三角形的面积＝底×高÷2，S＝ah÷2。

学生在已有的直角三角形的活动经验上，能够自主利用方法再次迁移，由特殊到一般，从而让推理过程更严密。通过大量的对三角形面积转化过程的体验与感悟，使学生对三角形面积公式的理解更为清晰和深刻，真正构建起三角形面积计算的模型，学生的思维从模糊到清晰，从残缺到完整，甚至从错误到正确，不断完善自己的思维。

环节三：延长体验过程，强化学生思维

公式推导完成后，接下去就是大量的公式应用，这样的教学，学生又回到枯燥的公式套用上，之前的大量探究就显得多此一举。因此，可以通过练习让学生的体验延续，思维得到进一步强化。

【教学片断3】

1.课件呈现基本练习

师：你们学得都很棒！现在老师要来考考你！请看屏幕（课件出现原始三角形，如图6）。

图6

师：如果让你求出这个三角形的面积，你会想到哪些转化方法？静静地想一想。（让学生只在脑海中想，不作交流）

课件依次呈现图7 中左侧的四张图。

图7

师：这些转化方法你想到了吗？

接着同时出示图7 中右侧的3 个算式。

师：现在请你将转化的方法和匹配的算式连一连。

师：（课件出示答案）请看大屏幕，和你连的一样的请举手。

2.呈现拓展练习

请你在图8 中画一个三角形，使它的面积与平行四边形的面积相等。（每相邻两点之间的距离为1）

图8

师：看来，这些数学问题都难不倒大家。下面我们继续研究，请看大屏幕，自由地读一读要求。同学们，题目读完了，会吗？请在《学习单》上试一试。

（1）展示底是4，高是6 的作品（如图9）。

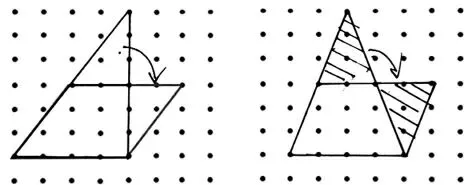
图9

师：我们先来看这两位同学的作品，先请他们说说他们是怎么画的？

生：沿着高的一半剪开就可以拼成前面的平行四边形。

师：他很会思考！同学们，我们一起观察，当三角形的面积和平行四边形的面积相等，并且底也相等时，那么它们的高有什么关系？

生：三角形的高是平行四边形的高的2 倍。

（2）展示底是8，高是3 的作品（如图10）。

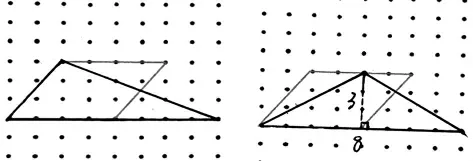
图10

师：我们再来看这两幅作品，谁能猜猜他们是怎么想的？

生：沿着底的一半剪开就可以拼成前面的平行四边形。

师：你表达得很清晰！同学们，这时候两个三角形的底、高、面积之间有什么关系吗？

生：当三角形的面积和平行四边形的面积相等，如果高也相等时，那么三角形的底是平行四边形的底的2 倍。

（3）展示底×高＝24 的作品（如图11）。

图11

师：这两位同学画的三角形底和高都不相等，面积会相等吗？

生：面积相等，因为底和高相乘都等于24，再除以2 就都等于12 了。

师：原来只要做到底×高等于24 就可以了。

两个练习注重的依然是转化的思想本质，利用想象、连线、画图等方法延长转化过程的体验，学生感悟到的是一种数学本质，而非一个冷冰冰的公式。同时，培养学生的空间观念和逆向思考的能力，以及万变不离其宗的哲学思维，尤其对三角形面积计算公式这一数学模型有了更为深刻的建构。

学习是自内而外的生长，在提倡“生本教育”的今天，数学课堂教学要时刻想着学生会怎么想，学生会怎么做，切勿给他们过多的材料“暗示”。只有基于“思维”而教、围绕“思维”而学，才能将学生置于教学的核心地位, 顺应学生主动探索，促进思维自然生长。