基于速度和位移反馈的圆柱涡激振动主动控制研究1)

邹 琳 王家辉 王 程 郑云龙 徐劲力

(武汉理工大学机电工程学院,武汉 430070)

引言

随着新能源的发展以及风能、海洋能的利用,人们发现可以将蕴藏在流体中的能量挖掘出来以一种新的能源形式加以利用[1].流体绕过钝体形成的不对称涡脱能使钝体产生涡激振动[2-3],Bernitsas 等[4]发现能利用海水绕过圆柱体产生涡激振动来发电,之后西班牙公司 Vortex Bladeless 发明了一种无叶片式风力发电机[5],利用结构的涡激振动将风能转化为电能.利用涡激振动发电关键性问题在于如何提高能量捕获效率,因此稳定控制与增强涡激振动对于提升其发电效率具有重要意义.

圆柱涡激振动控制按照是否有能量输入的方式一般分为被动控制和主动控制.目前增振被动控制的技术主要关注柱体的结构参数,Bahmani 等[6]研究了层流状态下,质量和阻尼比对圆柱涡激振动的影响,发现质量比或阻尼比的减小会增大振动幅值.Barrero-Gil 等[7]研究了质量比和机械阻尼对圆柱能量转换的影响,发现最大俘能效率主要受质量阻尼参数的影响.邹琳等[8]将表面结构斜率参数引入波浪型圆柱,提出波浪锥型圆柱,发现改型后柱体较直圆柱振动幅值与锁频区间都有一定增长.Zhang 等[9]研究了4 个圆柱不同排列间距对振动的影响,发现在一定的间距下,下游的圆柱振动幅值会被增强.Quadrante 等[10]对于运动中的圆柱表面进行不同角度的线布置,发现布置在60°和75°的角位置会加剧圆柱体的振动.Luis 等[11]实验研究发现附加线后圆柱体俘能最大效率大约是光滑圆柱体的4 倍.Kiu 等[12]研究了表面粗糙度对圆柱涡激振动的影响,发现圆柱体粗糙度会影响最大响应幅度和最大平均阻力系数.主动控制则是通过外部输入能量来控制流动.Mackowski 等[13]和 Huynh 等[14]通过外部能量输入将非线性刚度元素附加到系统中,利用反馈控制改变系统结构运动方程参数来实现增振.Ramlan 等[15]发现在低工作频率范围下双稳态刚度会提高获取的能量.Huynh 等[16-17]量化了阻尼和双稳态间隙控制参数,并提出OGY 控制算法,通过将其应用到所需的周期振动来稳定混沌响应,成功地提高了能量捕获功率.然而湍流的复杂特性使这些研究流体控制的方法仅局限于简单的被动控制和开环能量输入,未能很好利用流场中的流体信息.

机器学习(machine learning,ML)提供了丰富的技术从数据中提取信息[18],在机器人控制[19]、自动驾驶等[20]控制领域都有着大量的应用.随着计算机性能的提升,研究者逐渐将机器学习应用于流动控制当中.Ren 等[21]采用遗传规划算法,以数据驱动和无监督的方式选择显式控制律,通过控制固定位置的吹吸气成功有效抑制了涡激振动振幅.Paris 等[22]针对圆柱层流下的减阻问题,使用改进的近端策略优化算法优化了圆柱后方信息采集传感器布局.任峰[23]通过近端策略优化算法控制旋转激励,成功使涡激振动振幅大幅降低.机器学习算法中的遗传算法(genetic algorithms,GA)目前已经成功应用于流场的主动控制[24].Li 等[25]使用基于遗传算法的优化来直接控制类车体的尾流,在减阻方面得到了很好的效果.陈东阳等[26]基于Van der Pol 尾流振子模型、结构动力学理论和遗传算法,建立了非线性能量阱(nonlinear energy sink,NES)减振装置优化设计仿真模型,抑制了柱体结构的涡激振.Benard 等[27]在实验中通过遗传算法实现了自主多变量的优化,同时优化等离子体放电的高压信号的电压幅度、突发频率和占空比,实现了后向台阶湍流控制的最优条件.Minelli 等[28]利用大涡模拟和遗传算法研究了阻力最小的驱动器参数,结果表明遗传算法选择了自然涡脱频率的超谐波频率,实现了使阻力最小化的有效驱动.

可见,引入智能算法是目前实现钝体涡激振动主动控制非常有效的手段之一.本文将以实现圆柱增振为目的,采用遗传算法优化的神经网络与圆柱涡激振动数值模拟相结合,基于速度反馈和位移反馈增益机制以实现改变振动系统的阻尼和频率,研究不同折合流速下(Ur=3.5～8),神经网络得到的速度反馈增益kv与位移反馈增益kd对圆柱增振的影响机理,为钝体绕流主动流动控制探索新方法.

1 理论模型和求解方法

1.1 受控圆柱涡激振动理论模型

二维圆柱涡激振动系统可以看成是一个弹簧质量系统[29],如图1(a)所示.图中x为来流方向,假定圆柱沿着纵向长度的横截面是均一的,只考虑单位长度的运动,不受任何控制的结构运动的方程为

图1 二维涡激振动系统结构示意图Fig.1 Schematic diagram of a two-dimensional vortex-induced vibration system

其中,ρ 为流体密度,D为圆柱直径,U是来流速度,CD,CL0分别为阻力和升力系数,其值大小采用Facchinett 等[30]给出的数据:CL0=0.3,CD=1.2.无量纲q(t) 表示尾迹的运动,代表圆柱的瞬态升力与固定在水中的升力之比.当速度反馈和位移反馈施加之后,如图1(b)所示,运动控制方程变为

其中kv和kd分别表示速度和位移反馈增益.为了获得圆柱涡激振动响应,利用Van der Pol 方程来描述尾迹运动

式中,λ 和P为经验参数,通过实验参数拟合分别为0.3 和1.2;ωs为涡脱频率,可以表示为 ωs=2πS tU/D.上述方程中的参数值详见表1,结构的固有频率fn=ω0/(2π)=10 Hz.采用4 阶龙格-库塔方法可以获得圆柱的涡激振动响应.Van der Pol 尾流振子模型虽然在低折合流速下的计算结果会产生一定误差,但基本上可以捕捉到柱体的涡激振动特性[31],将该模型计算结果用于神经网络选取kv,kd组合是可行的.

表1 计算模型参数Table 1 The parameters of computational model

1.2 遗传算法优化神经网络计算框架

神经网络的结构由两个隐藏层和一个输入输出层组成,网络的神经元个数分别为 1×10×5×2,种群数量为N.对每一个个体而言按照图2 中所示的方式进行解码得到神经网络.以指定范围的10 种折合流速(Ur=3.5,4,4.5,···,8)作为该神经网络输入,输出速度和位移反馈增益大小.将得到的反馈增益作用于耦合方程式(3)和式(4),从而得到反馈增益下的振动幅值比.如果这个振动幅值比达到了事先设定的目标范围(如0.6～0.8),那么这个神经网络的适应值加 1,否则,在指定的折合流速下,神经网络的适应值加 0.具体的评价标准如下

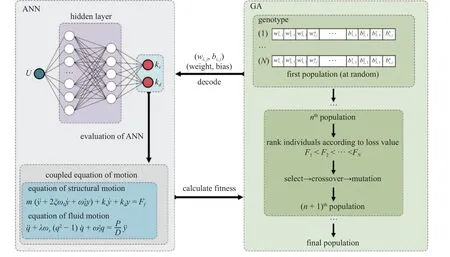
图2 利用遗传算法寻找最优的神经网络结构参数的计算框架Fig.2 A computational framework for the optimal neural network structural parameters by employing the genetic algorithm

式中,F(Ur) 表示折合流速Ur下,神经网络的适应值,Ar表示该流速下涡激振动的最大振动幅值.因此,整个计算目的就是要找到一个合适的神经网络,使得在给定流速范围内都能满足振幅比的要求,即

按照上述神经网络评价标准,一个神经网络最大的适应值为10,最小的适应值为0.根据每个神经网络的适应值不同对个体进行排序,随后进行选择、交配和变异这3 种遗传方式产生下一代个体.通过这种方式,进化一定数量的代数后,遗传算法能够寻找到满足条件的神经网络.

遗传算法的参数设置如表2 所示.在遗传算法参数的设定中,应该着重关注两个参数: 种群数量和进化代数[32].图3 所示为种群数量对进化过程能够达到最大适应值的影响.从图中可以看出,当种群数量为100 和120 时,最终神经网络控制振动的表现趋向于稳定,每一次样本进化得到的神经网络最终适应值都能达到10.因此本文种群数量均设置为100 来进行计算.找到最优神经网络之后,将神经网络输出的反馈增益值作用于公式(3),然后利用4 阶龙格库塔法求解受控状态下的耦合方程,得到圆柱的振动位移.利用Fluent 中的用户自定义函数(UDF)实现上述过程.

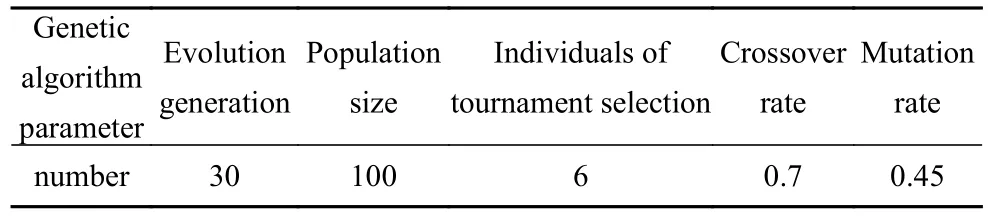
表2 遗传算法参数设置Table 2 Genetic algorithm parameters

图3 不同种群数量对最大适应值的影响Fig.3 The effect of different population sizes on maximum adaptation values

1.3 网格划分和边界条件

本文基于CFD 商业软件FLUENT 和结构动力学原理,通过UDF 及嵌套网格技术建立了单自由度圆柱涡激振动的数值模型.数值计算中的计算域为长方形,图4(a)所示,大小为40D(顺流向)×20D(横流向).进口和出口到圆柱中心的距离分别为10D和30D.计算域的横流向尺寸距圆柱中心从-10D到10D,动网格策略采用重叠网格(overset)模型,选择围绕圆柱体的直径为6D的圆形区域作为前景网格,它是跟随圆柱体运动的伴随移动区域.前景网格大小由圆周节点数L和半径节点数d定义(图4(c)),背景网格在前景网格运动周围进行加密,大小由节点数H定义(图4(b)).入口处采用狄利克雷边界条件,即u=U∞,v=0 (u和v分别为x,y方向上的速度(单位: m/s)),出口处的边界条件采用诺曼边界条件,即 ∂u/∂x=0,∂v/∂x=0,计算域的上下面为对称边界条件,即 ∂u/∂x=0,v=0,圆柱表面为无滑移边界条件,即u=0,v=0.

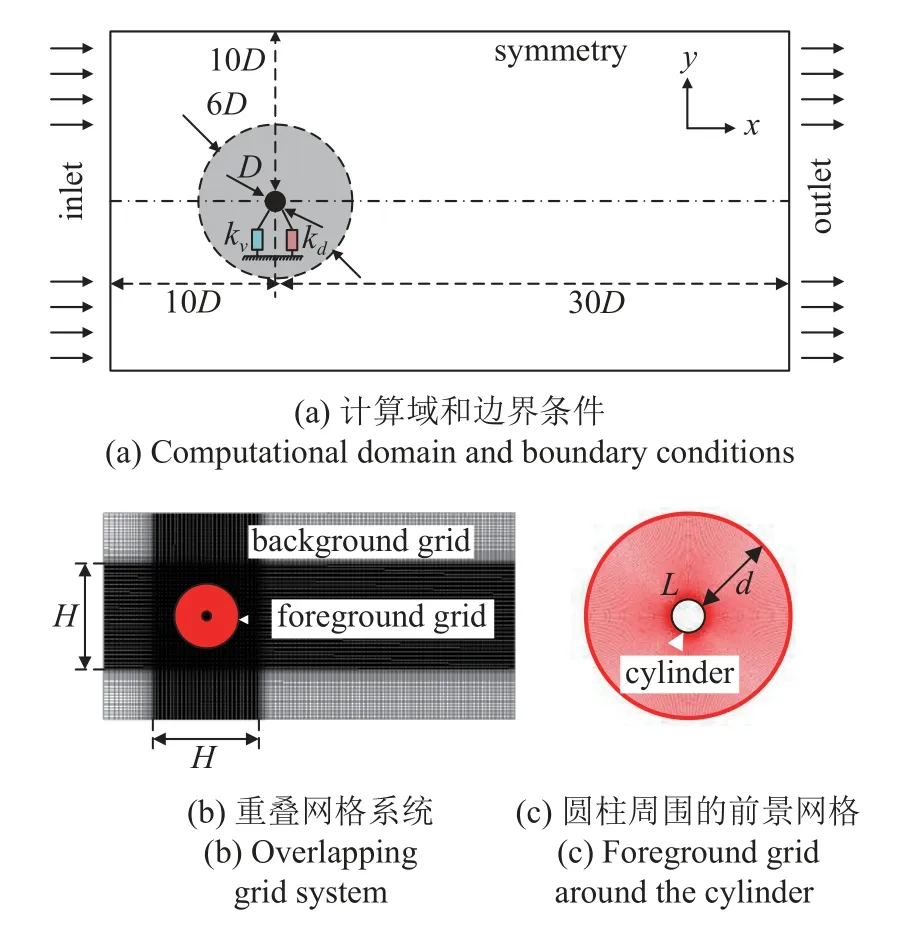
图4 计算域,边界条件和网格组成示意图Fig.4 Schematic diagram of computational domain,boundary condition and mesh composition

2 数值计算模型验证

2.1 网格及时间步长独立性验证

如表3 所示,M1,M2,M3 代表同一时间步长下3 种网格密度对圆柱振幅比的精度影响,在时间步长Δt=0.003 s 时,随着网格数量的增大,可以清楚地看到M2 和M3 之间的振幅比差异下降到小于0.5%,判定振幅比收敛于M2,因此在数值模拟中选择了M2 的网格划分策略.M2,M4,M5 为同一网格密度下时间步长对振幅精度的影响,可看出随着时间步长减小(Δt=0.003～0.001 s),振幅比的影响可以忽略不计,因此时间步长选择Δt=0.003 s.

表3 重叠网格数量无关性验证(无反馈控制,Ur=5)Table 3 Validation of the number of overlapping meshes(no feedback control,Ur=5)

2.2 UDF 合理性验证

首先使用UDF 程序对圆柱进行仿真计算,计算仿真参数为: 圆柱直径D=0.02 m,固有角频率 ω0=62.83 rad/s,圆柱质量比m*=2.47,折合流速Ur=2.4～12,流体密度为ρ=1.225 kg/m3,流体动力黏性系数为1.79×1 0-5m2/s.将计算结果与实验结果进行对比.

本次实验验证风洞试验段截面尺寸为450 mm×450 mm,实验台架前后壁面各有一个可拆卸的盖板,直径为280 mm,经过测量该模型的边界层厚度为18 mm,可以认为模型处于均匀流场之中,根据相似性原理,实验模型3:1 等比例放大,圆柱直径为60 mm,长度为445 mm,采用中空设计,厚度约为1.5 mm,圆柱的材料为8200 Pro 树脂,采用3D 打印技术,质量比为m*=15.8,由位移自由衰减曲线可求得模型固有频率fn=9.27 Hz,阻尼比ξ=0.000 21.圆柱模型上下两端开孔方便炭纤维杆支撑固定并连接到尼龙线,一端连接挡板,挡板下方安装激光位移传感器,当圆柱振动时由传感器进行振动位移采样,采样设备包括示波器,电源,控制器和激光头.实验台架及实验原理如图5 所示.

图5 实验装置示意图Fig.5 Schematic diagram of the experimental setup

图6 为圆柱涡激振动最大振幅比随折合流速变化曲线图,从数值仿真结果来看,其曲线整体变化趋势和锁频区间与Singh 等[33]和黄继露[34]的仿真结果基本保持一致.黄继露[34]与Singh 等[33]的仿真质量比分别为m*=2.0,m*=10.0,本文数值仿真中质量比m*=2.47,小于Singh 等[33]的仿真质量比.并且本文的雷诺数范围为Re=600～3200,黄继露[34]与Singh 等的仿真雷诺数Re=100,因此数值计算的振幅比会大于文献中的数值仿真结果[35].与实验结果来对比看,由于实验采用相似性原理,对实验圆柱进行3:1 放大,因此实验数据与仿真数据存在一定差异,但振动幅值仿真计算结果的曲线变化趋势大致相同,锁频区间也较好地吻合,因此可以认为本文的数值计算模型使用的UDF 程序是有效的.

图6 本文数值仿真结果与实验结果和文献结果对比Fig.6 The numerical simulation results are compared with the experimental results and literature results

3 结果和讨论

3.1 速度反馈和位移反馈的影响

分别调整kv和kd的大小,观察不同折合流速下涡激振动幅值大小,当速度反馈增益减小时,会使系统在共振区间内的幅值增加(见图7(a)).当位移反馈增大时,共振区间向右移动,意味着发生共振的起始流速增加(见图7(b)).可以看出,速度反馈能够改变系统在共振区间的幅值,位移反馈能够改变共振区间的范围.如果将二者结合起来,就能够实现在一定的流速范围下,结构的振动幅值稳定在给定目标范围内(0.6～0.8),如图7 中的绿色区域所示.

图7 速度反馈和位移反馈对振幅比的影响Fig.7 The effect of velocity feedback and displacement feedback on vibration amplitude ratio

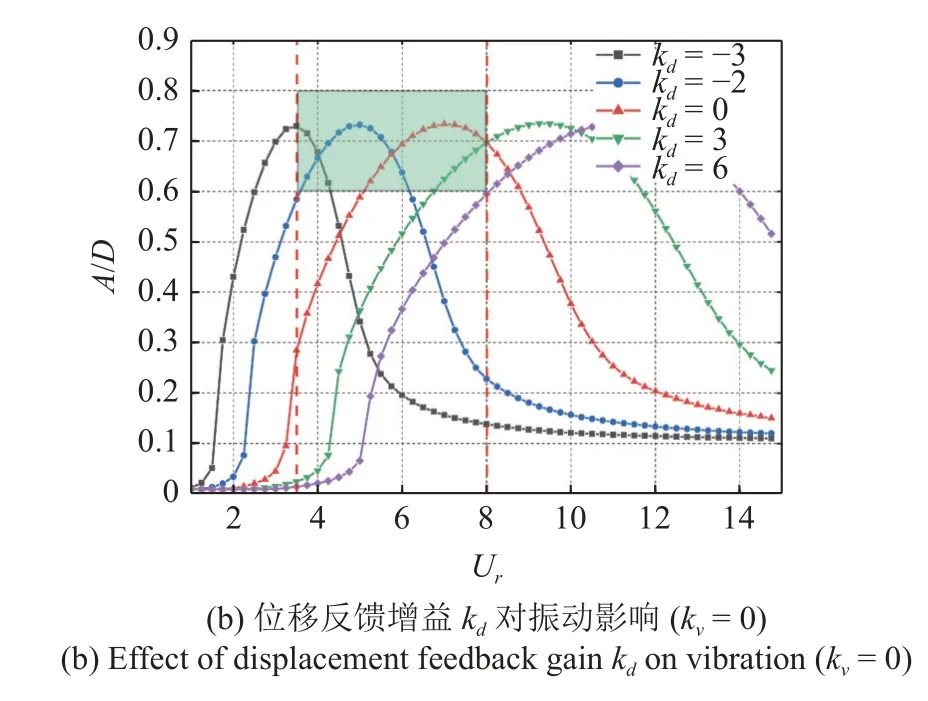
图7 速度反馈和位移反馈对振幅比的影响 (续)Fig.7 The effect of velocity feedback and displacement feedback on vibration amplitude ratio (continued)

3.2 基于神经网络的圆柱涡激振动控制

记 N eti,i=0,1,2,···,9 表示种群数量为100 时遗传算法搜索出的10 个不同的神经网络.10 个神经网络输出的kv和kd变化趋势有一部分是类似的,因此只分析4 组具有代表性趋势的神经网络输出结果.图8(a)和图8(b)所示为4 个不同的神经网络在目标折合流速Ur=3.5～8 内输出的速度反馈kv和位移反馈kd的变化情况.对于 Net1和 Net2而言,神经网络输出的速度反馈增益基本上随着流速的变化保持不变,而位移反馈增益随着流速的增加而增加.对照图8(c)和图8(d),可以发现在这两个神经网络的控制下,目标流速内的振幅比基本上呈现先增大后减小的趋势.通过透明曲线的变化趋势可以看出,随着位移反馈kd的增加,透明曲线向右移动,这与图7(b)所示的变化规律是一致的,但是在移动的过程中最大峰值在逐渐减小,这与单纯的只有kd作用时的变化规律(图7(b),峰值基本保持不变)并不一样,这说明速度反馈和位移反馈共同作用时对涡激振动系统的振幅影响是非线性的.对于 Net3而言,目标流速内的振动幅值比变化曲线呈现“尖端”点,在Ur=5.5 时振幅比突然增大,这主要是由于kv突然变化导致的(图8(a)).而且受控作用下的振幅比呈现先减小后增大的变化趋势,这主要是由图8(a)中kv的绝对值先减小后增大所造成的.最后通过 Net4可以看出,随着kv绝对值的减小,系统的振动幅值逐渐减小,然后趋于不变.另外透明曲线的峰值点逐渐向右移动,这主要是由于kd的不断增大所造成的.

图8 折合流速 Ur=2.5～14.5 时,圆柱在4 种神经网络的4×10 组输出增益下涡激振动幅值比Fig.8 The amplitude ratio of vortex-induced vibration of the cylinder under the output gain of 4×10 groups of 4 neural networks(Ur=2.5～14.5)

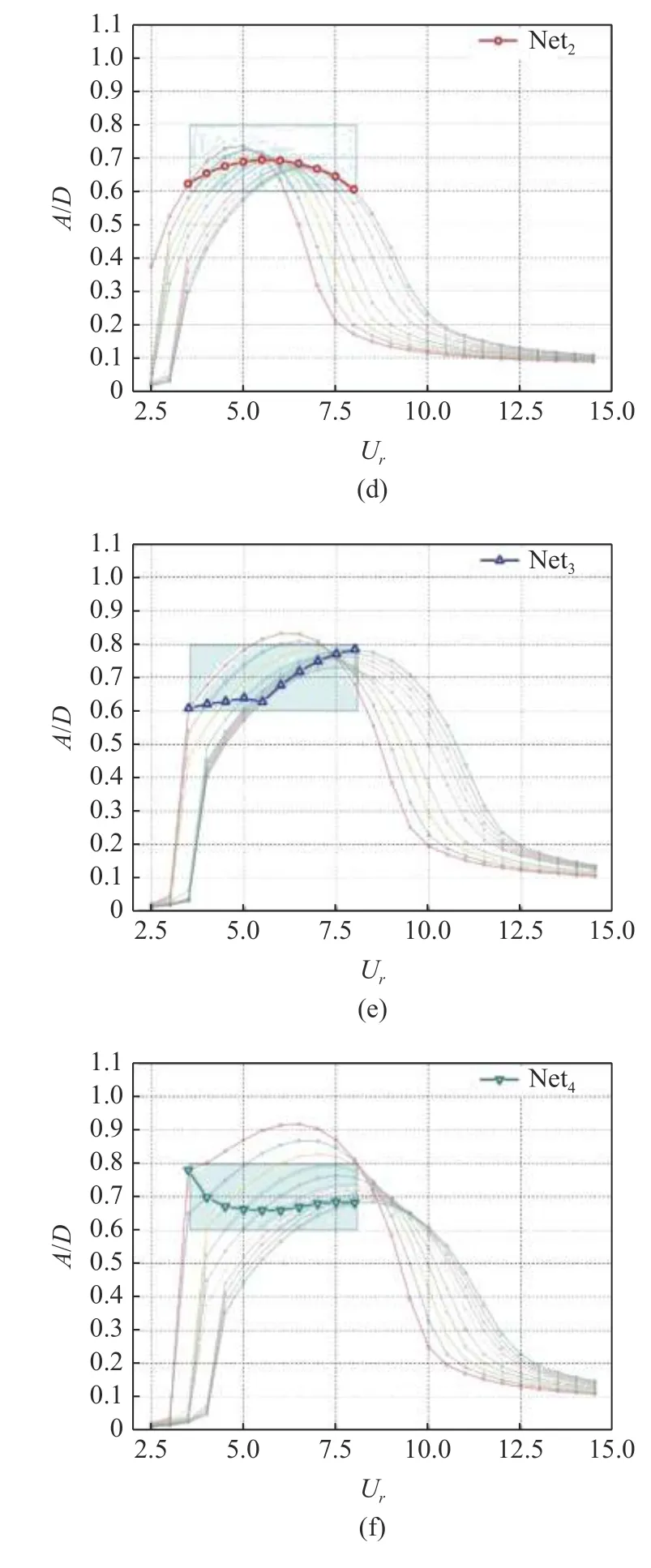
图8 折合流速 Ur=2.5～14.5 时,圆柱在4 种神经网络的4×10 组输出增益下涡激振动幅值比 (续)Fig.8 The amplitude ratio of vortex-induced vibration of the cylinder under the output gain of 4×10 groups of 4 neural networks(Ur=2.5～14.5) (continued)

通过上述的讨论可以发现,神经网络在目标折合流速内输出不同的kv和kd能使系统振幅比保持在目标范围内,通过这种方式实现了涡激振动增强.值得注意的是,虽然遗传算法最终找到的神经网络都能满足在目标流速范围内达到目标振幅比的要求,但是正如图8 所示,不同的神经网络对系统振幅比的影响是不同的,例如 Net1和 Net2控制的振动幅值比是先增大后减小的,明显不同于 Net3和 Net4作用时候的情况.而且,通过进一步观察图8(f)可以发现,尽管 Net4能够实现目标振幅比的要求,但是从浅色曲线可以看出,对应的浅色曲线的峰值明显要高于其他3 个神经网络控制时的情况,这是由于 Net4输出了相对更大的反馈增益系数kv和kd(图8 所示).因此为了考虑神经网络输出的速度反馈和位移反馈的大小,将kv和kd无量纲化,引入以下表达式

式中,J代表神经网络输出增益所消耗的总能量,Jv(速度反馈增益能量消耗)和Jd(位移反馈增益能量消耗)分别表示速度和位移反馈增益相对于系统阻尼和固有频率的大小,这两个值反映了主动控制过程中外部能量的输入.权重系数C代表含义是惩罚参数,用于优先考虑Jv或者Jd对总体能量消耗的影响,取C=0.01.因此神经网络需要满足下式约束条件

其中Ui表示目标折合流速范围Ur=3.5～8 内的10 个流速.

图9 所示为未施加约束和施加约束后10 个神经网络对应的总能量消耗值,从图中可以看出,未施加约束时,增益能量消耗的平均值为7.911,当施加式(8)的约束之后,平均值为5.294,降低约33.08%,说明约束的添加能够在满足振幅比控制要求的前提下尽量保证能量消耗较少.且施加约束后,样本标准差为0.243,说明由遗传算法寻找到的不同的神经网络输出的反馈增益能够达到一个稳定的值,这对提高控制系统的稳定性是有利的.

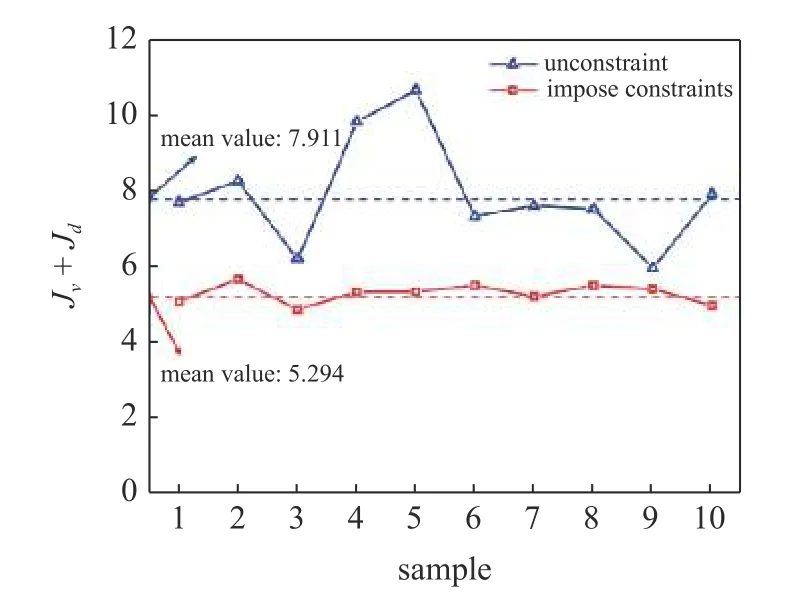
图9 不施加约束和施加约束情况下10 个不同的样本的J 值,种群数量为100Fig.9 J values for 10 different samples without and with constraints imposed,the population size is 100

图10 展示了施加式(8)约束后,由遗传算法找出的4 个不同的神经网络在折合流速范围内输出的反馈增益大小以及振幅变化曲线.从图10(c)可以看出,随着折合流速的增加,不同kv和kd的组合使得透明曲线在向右移动过程中峰值不断减小,这主要是由于 Net1输出的kv绝对值在逐渐减小导致透明曲线峰值减小,kd逐渐增大导致透明曲线向右移动.观察图10(a)和图10(b),对于 Net3而言,当折合流速大于6 时,神经网络输出的速度反馈kv和位移反馈kd基本保持不变,对应于图10(e)可以看出,透明曲线的位置保持重合,某一条特定的幅值比曲线可以满足在目标振幅比范围内的要求.另外,观察图中的 Net4,发现神经网络输出的速度反馈kv绝对值逐渐变大(图10(a)),意味着系统在共振区间的振动幅值会逐渐变大,而位移反馈从-2.47 到0.88,意味着共振区间会逐渐向右移动,但是观察图10(f)图中的透明曲线可以看出,透明曲线的最大峰值在向右移动过程中基本保持不变,这就再次说明了速度反馈和位移反馈共同作用时对系统振动幅值的影响是非线性的.从图10(c)～图10(f)可以看出,在目标折合流速范围内,系统在神经网络的控制下,振动幅值比基本维持在0.6～0.7 之间,处于目标振幅区间的下半部分.特别地,对于 Net2和 Net4而言(图10(d)和图10(f)),系统的目标振幅在满足共振区间的条件下基本接近于0.6,因此增加式(8)约束对提高系统振动的稳定性是有意义的.

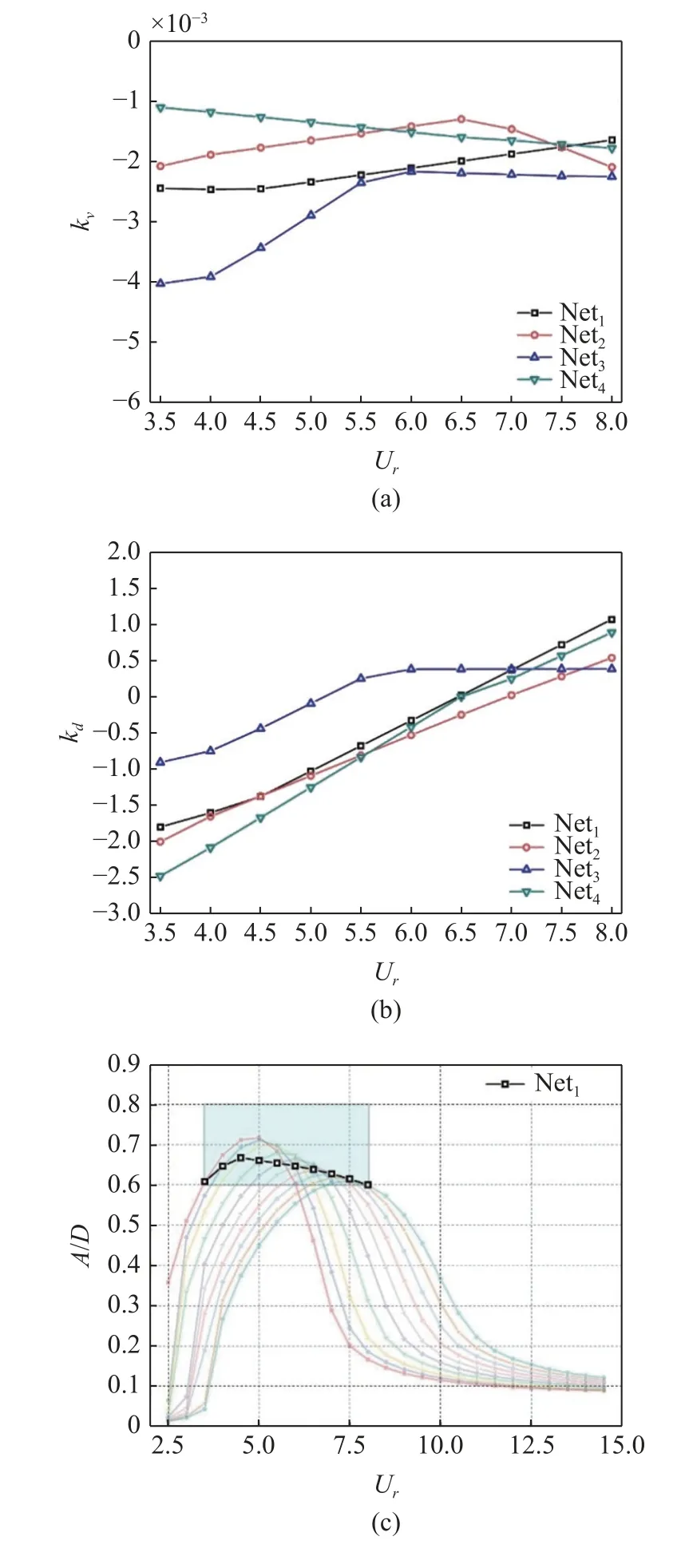
图10 (a)～(b)施加反馈约束后的输出反馈增益以及(c)～(f)反馈增益下的振动幅值比Fig.10 (a)～(b) Output feedback gain with feedback constraint applied and (c)～(f) vibration amplitude ratio at feedback gain

3.3 受控和未受控圆柱的涡量图

为了分析速度和位移反馈的控制效果,选取图10中 Net1输出速度和位移反馈增益来控制二维圆柱的振动.首先引入无量纲时间t*=u∞t/D,u∞是自由来流速度.图11 分别展示了在Ur=3.5,8 时受控与未受控的涡量图.从图中可以看出,Ur=3.5 时,随着时间的增加,对于未受控情况观察不到涡脱现象,当施加反馈增益之后,在振动达到稳定时明显出现漩涡脱落,呈现“2S”的涡脱形式,并且圆柱在平衡位置处上下振动.从图12 可以看出,对于未受控情况,圆柱的振动幅值和速度基本为0,这与涡量图相对应.当施加速度和位移反馈后,处于稳态时振动幅值比显著增加,且达到了事先设定的目标振幅比内(0.6～0.8),说明反馈增益为系统提供了能量来源,激发了结构的振动和漩涡脱落.

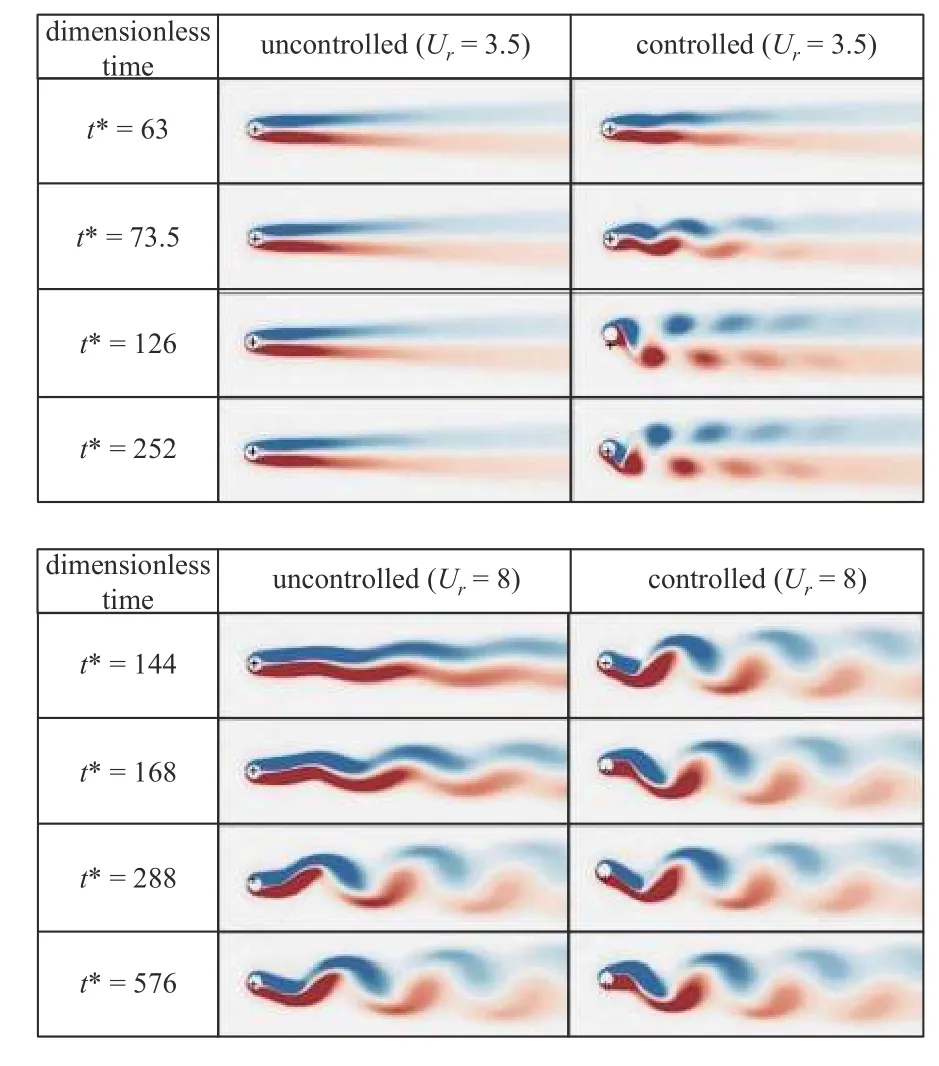
图11 圆柱振动涡量图,“+”符号表示圆柱的平衡位置Fig.11 Vibration vortex structures of the cylinder,The symbol “+”indicates the equilibrium position of the cylinder

图12 圆柱振动位移和速度相图Fig.12 Diagram of vibration displacement and velocity of the cylinder

当折合流速Ur=8 时,在图11 中可以观察到对于受控状态,系统的起始振动时间明显要早于未受控情况,例如无量纲时间t*=144 时,受控状态下后方的漩涡脱落比未受控状态更加明显.观察图12 发现对于未受控情况,系统的振动幅值比为0.439,未达到指定的振动幅值比范围.当施加反馈增益之后振动幅值为0.606,增加了38.04%,这说明施加增益来改变振动幅值的策略是可行的.而且观察图12 可以看出,施加速度和位移反馈后,结构的振动速度由0.557 m/s 变为0.855 m/s,增长了53.5%,这对于利用结构的振动速度来获取能量的应用是有价值的.

图13 所示为在受控和未受控状态下,振动位移和升力随时间的变化关系.从图13(a)可以看出,在折合流速Ur=3.5 时,圆柱受控状态下的振动要比未受控明显增加.当折合流速Ur=8 时,反馈增益作用在系统上之后不仅能够增加圆柱的振动幅值,而且也会使得圆柱涡激振动的起振时间提前.从图13(b)可以看出,在受控状态下,折合流速Ur=3.5 时圆柱受到的升力系数为0.947,要大于Ur=8 所受到的升力系数0.161,这是因为低折合流速(Ur=3.5)下的圆柱本身不发生涡激振动,而高折合流速下(Ur=8) 圆柱体会存在一定的振动,因此要使得在Ur=3.5 时圆柱的振动幅值比达到指定范围,此时需要的外部能量会更多,因此升力系数也会相应越大.图14展示了在两种不同折合流速下,对应于受控和非受控振动位移和升力的频谱.对于Ur=3.5 来说,施加了反馈之后振动幅值明显增加,振动频率为7.33 Hz(图14(a))高于未受控时的振动频率6.12 Hz,进一步观察发现受控后的振动频率低于结构的固有频率(fn=10 Hz).对于Ur=8 来说,未施加反馈增益时,系统振动频率为10.13 Hz (图14(c)),这和结构的固有频率基本保持一致,因为此时系统处于自由涡激振动状态,不存在外部激励强迫系统振动.当存在反馈作用时,结构的振动频率和涡脱频率都会加快,这说明在高折合流速情况下施加反馈增益后,会使系统振动频率高于结构的固有频率.对于升力系数而言,特别是在折合流速Ur=8.0 时,由于反馈增益的施加,升力系数变化曲线的高频范围会增大(图14(d)中由30.17 Hz 增加到33.5 Hz,增加了约11.04%).而且对于受控情况,不管是低折合流速还是高折合流速,圆柱的振动频率都要高于非受控情况,不再受到固有频率的支配.

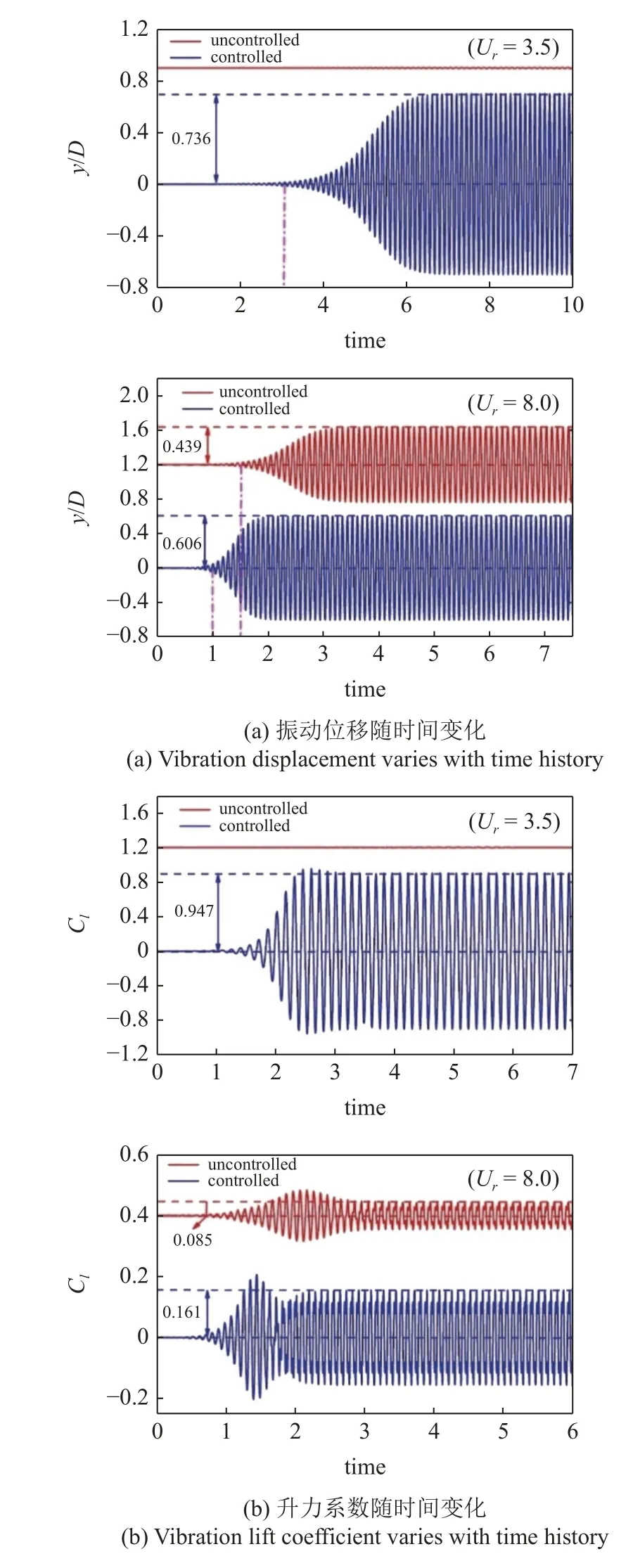
图13 折合流速 Ur=3.5,8 时,圆柱的振动位移和升力系数时间历程变化曲线Fig.13 The time history of the vibration displacement and lift coefficient of the cylinder (Ur=3.5,8)

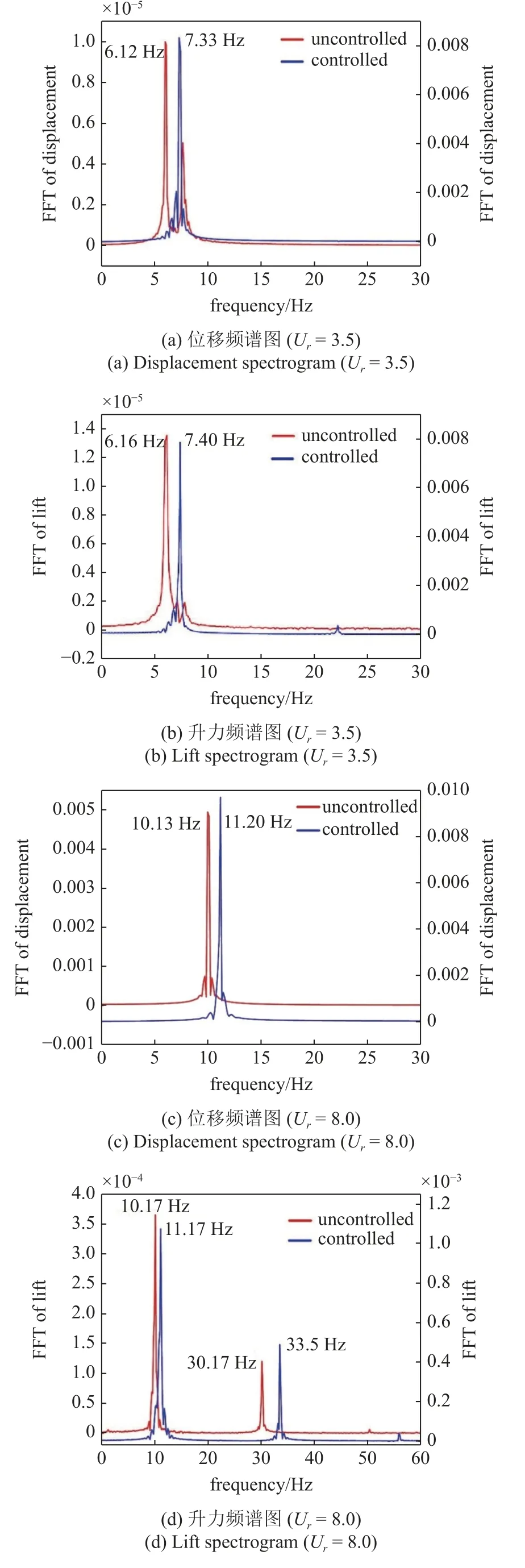
图14 圆柱位移和升力的频谱图Fig.14 Spectrogram of displacement and lift force of the cylinder

4 结论

本文将折合流速作为输入,通过遗传算法优化的神经网络控制速度反馈和位移反馈增益,以此来实现二维圆柱的涡激振动增强,这对利用振动获取可再生能源有重要的意义.本文的主要结论如下.

(1)利用速度反馈结合位移反馈的方式,能够实现在一定的流速范围内使圆柱的振动幅值保持在一个稳定的值附近.利用这种方式,借助神经网络来映射流场速度与反馈增益值大小之间的关系,最终在折合流速范围Ur=3.5～8 内圆柱的振动幅值比保持在0.6～0.8.

(2)加入反馈增益约束后,平均能耗J低于无约束情况,从7.911 降低到5.294,降低了33.08%.而且,受约束的最优表现的神经网络控制的目标幅度接近0.6,有利于提高系统的稳定性.

(3)通过对非受控和受控情况下的振动分析,发现在Ur=3.5 时,反馈增益为涡激振动系统提供了激发振动的能量来源,并且可以明显观察到涡流脱落和涡度.当折合流速Ur=8 时,受到反馈增益作用之后,圆柱振动速度增加了53.5%,且起振时间早于非受控情况,说明外部激励控制能够增加结构的振动速度和起振时间.由于外部能量输入并激发涡激振动系统的振动,在相同边界条件下,受控状态圆柱的振动频率高于非受控状态,不再受固有频率支配,这将有助于提高系统的涡激振动.