温度敏感凝胶推进剂中气泡运动特性研究1)

2023-10-29宋春雨李梦哿吴威涛

力学学报 2023年9期

宋春雨李强周昊李梦哿封锋吴威涛

(南京理工大学机械工程学院,南京 210094)

引言

凝胶推进剂是指将胶凝剂添加到液体推进剂中形成的一种新型推进剂,一般表现出剪切变稀的非牛顿流变特性,且能够有效地降低液体推进剂的挥发性,是一种能长期保持稳定的推进剂体系[1].剪切稀化流体是最常见的非牛顿流体,其特征是表观黏度随着剪切速率的增加而降低,所以可以使用一种考虑了流体零剪切速率和无穷剪切速率下黏度的本构模型即Carreau-Yasuda 模型对凝胶的流动特性进行模拟[2-3].凝胶的剪切稀化特性使其在剪切速率较低时表现出固体特性,在剪切速率较高时表现出流体特性,因而兼具了固体推进剂和液体推进剂的优点[4].本文所研究的凝胶在低剪切速率下并未表现出弹性效应,所以研究中构造的本构模型并未考虑弹性效应.由于凝胶复杂的流变学特性,难以通过简单的经验总结方式进行精确控制,因此需要对其流变特性进行系统研究,以指导其制备、贮存、填装和使用等过程[5].而在凝胶推进剂的制备和加注过程中,气泡的混入是难以避免的,这可能会导致推力振荡、推力断续或熄火等问题.此外,气泡的混入还会影响推进剂的传热性能和泵的气蚀现象[6].所以对于凝胶推进剂中气泡运动行为的探究有重要的意义.

大量的学者研究了气泡在非牛顿流体中的运动情况并探讨了流体的流变特性对气泡运动的影响.Premlata 等[7]的研究发现气泡在牛顿流体中可以保持直线上升,在非牛顿流体中气泡的运动轨迹与流体的流变指数与特征时间都有关系.Davidson 等[8]的研究表明,在黏性流体中,气泡上升的速度与液体的黏度成反比,与液体的密度成正比.同时Zhang等[9]在实验和数值上研究了大密度和高黏度的剪切稀化流体中的气泡动力学问题.其使用Carreau 流变模型作为液相的力学模型,并观察到气泡尾部存在一个高黏性区域,这会影响尾随气泡的运动,同时剪切稀化流体中流变指数的下降会增加气泡的上升速度.还有研究表明[10],气泡变形随伽利略数(Ga)和厄特沃什数(Eo)的增加或流变指数的降低而增大.气泡终端速度随Ga数的增加而增大,随Eo数和流变指数的增加而减小.Abu-Nab 等[11]研究了表面张力对气泡半径、生成时间和气泡初始速度的影响.胡波等[12]研究了特征时间对气泡运动的影响,发现特征时间越大,气泡的终端速度越大.并且当表面张力较小时,气泡尾部出现黏度盲区.Li 等[13]研究了剪切稀化液中单气泡的上升,发现气泡周围的流线呈现对称分布,椭球型气泡的尾部流线更细长.姜韶堃等[14]的研究结果表明,高表观黏度流体的黏度随高度呈线性变化,导致气泡发生规律而可预测的形变,气泡的宽高比会随着高度的增加而线性变化,并且气泡的形状变化幅度相对较小.Fan 等[15]的研究结果表明,气泡的瞬时体积和分离体积均随孔径减小,随质量浓度和气体流量的增加而增大.分离时的长径比随孔径和质量浓度而增大,随气体流速的增加而下降.Liu 等[16]研究了非牛顿流体中3 个平行气泡的相互作用,发现气泡的水平间距大于临界间距时会使气泡发生排斥作用.Wang 等[17]的研究指出,气泡终端速度容易受壁面效应的影响.还有一些学者对屈服应力和黏弹性流体中气泡的运动进行了研究.如Xiang 等[18]研究了屈服应力流体中气泡的形成,发现微通道中液体流量的增加和气体流量的降低有利于提高气泡形成的均匀性.Aguirre 等[19]研究了在黏弹性液体中,随黄原胶浓度的增加,溶液黏度增加而气泡的速度减小.并发现气泡周围产生的涡流是气泡变形的原因.

除了流变指数、特征时间和表面张力等因素,温度对非牛顿流体的性质也会产生影响,Rahimi等[20-21]研究了温度对幂律模型中的稠度指数和流变指数的影响,发现温度对凝胶的幂律指数的影响不显著,而稠度指数随温度的升高而线性降低,同时在低温下凝胶的温度敏感性更强些.Ellahi[22]通过使用两种与温度相关的黏度模型,研究了非牛顿纳米流体的特性.他们发现黏度参数与温度呈现强烈的依赖性.

对于处理两相流问题有许多学者进行了研究并提出了改进方法.Klostermann 等[23]证实使用流体体积方法(VOF)研究气泡问题具有许多优点,例如能够保持界面的尖锐性和有界性、保证系统总质量的守恒以及计算快等.Garoosi 等[24]使用了改进版的流体体积方法,对具有不同密度的两个气泡的瞬态演变进行了数值研究.Reza 等[25]使用分段线性界面计算方法(PLIC)跟踪了两相流界面,通过连续表面力(CSF)模型计算表面张力,并在数值模拟中取得了两个连续斜坡处气泡运动的最大速度.Nahed 等[26]基于PLIC-VOF 方法,提出了一种新的曲率估计方法,大大降低了伪流动的影响,使得曲率计算精度更高.

目前对于温度敏感性凝胶的研究还主要集中在本构方程构建和物性实验测量等方面,对于气泡动力学研究还相对较少.本工作采用流体体积方法研究了在静止凝胶流体中,温度、特征时间、流变指数和表面张力对气泡形变和运动的影响,重点关注气泡的纵横比、速度、重心位置的变化趋势,以期为凝胶推进剂加注过程中的除气工艺提供研究基础.

1 物理模型和计算工况

1.1 物理模型

本文研究的气泡运动速度较小,三维效应不显著,因此为了节省运算时间,采用二维模型进行仿真研究.如图1 所示,计算域为一个二维矩形区域.Pang 等[10]采用二维模型仿真研究了气泡在非牛顿流体中的上升运动,与实验结果误差为12%.值得指出的是本文所简化的模型为二维无限大平板,与三维球形气泡存在差异.气泡初始位置位于A点受浮力驱动向上运动,其中L足够长,可以确保气泡的运动得到充分发展.由文献[27]可知计算域宽度的一半与气泡直径的比值超过10 时,气泡的终端速度趋于稳定,此时可忽略壁面效应的影响.本文研究的气泡半径较小,W/(2d)=12.5,所以壁面对气泡的运动影响可以忽略不计.矩形计算区域的宽度为W=0.15 m,高度为L=0.24 m,初始气泡中心A点与底部壁面距离为h=0.04 m,定义气泡初始位置为原点.网格尺度为0.000 2 m,一个气泡内约有700 个网格.

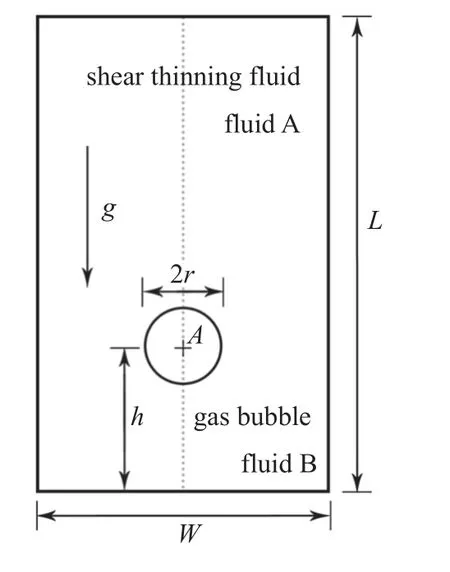
图1 示意图(非按比例)Fig.1 Schematic (not to scale)

假设气泡的初始形状为圆形,直径0.006 m,气泡的上升运动主要受重力、黏性力和表面张力的影响,其中重力加速度的方向向下.这些作用力对于气泡运动的影响可用伽利略数(Ga) 和厄特沃什数(Eo)进行表征.其中,Ga数表示重力与黏性力的比值,Eo数表示重力与表面张力的比值.其表达式为

其中,ρl表示液相密度,ρg表示气相密度,g表示重力加速度,d表示气泡初始直径,η0表示液相零剪切黏度,σ 表示表面张力,θ 表示温度.

1.2 边界条件

在模拟中,上端边界为压力出口边界条件(pressure outlet),而下端边界和左右侧面边界为无滑移壁面边界条件(wall).

2 控制方程和数值方法

2.1 控制方程

本文假设气液两相的流动均为不可压缩的且为层流,并忽略由温度变化引起的流体密度变化.Navier-Stokes 方程的守恒形式[28],包括连续性方程和动量守恒方程的公式如下

其中,U为速度,ρ 为流体局部平均密度,⊗ 表示张量积,p为压力,τ 为应力张量,F为运用连续表面张力模型得到的体积力源项,∇ 为哈密顿算子.其中,应力张量的公式如下

其中,µ 为流体当地平均黏度,D为应变率张量,其公式如下

流体局部平均密度 ρ 和平均黏度 µ 的计算如下

其中,α 为整个计算域的相函数,其定义见2.3 节;下标l 和g 分别表示液相和气相.利用连续表面张力模型[29],我们可以将表面张力当作体积力处理,计算体积力的方法如下

式中,σ 为表面张力系数,κ 为界面曲率,计算公式如下

本文研究的凝胶溶液与气体的黏度比值较大,约为 1 05,而凝胶溶液与气体的密度比为1 03.研究指出如果气液之间的黏度和密度比太大,则计算收敛非常困难[30].因而对于压力方程采用共轭梯度求解器和多重网格预条件器进行求解,为了保证数值求解的收敛性和稳定性,控制时间步长,使得库朗数最大在0.05 左右.同时,采用PIMPLE 算法来求解速度场和压力场的耦合问题,外部迭代50 次,内部迭代3 次.在网格上使用分段线性界面重建来处理流体界面上的不连续性,以实现数值求解的连续性.

2.2 液相本构方程

凝胶的剪切稀化特性采用Carreau-Yasuda 模型描述,根据局部剪切速率,可得到凝胶的当地表观黏度.Carreau-Yasuda 模型如下

重点考虑了温度对凝胶推进剂黏度的影响,并根据Andrade-Eyring 法则[31],使用Reynolds 模型来表示温度影响项[32],温度敏感剪切变稀凝胶的黏度本构方程如下

式中,η∞和 η0分别为无穷大剪切率和零剪切率时的黏度,λ为时间常数,b控制了黏度-剪切率曲线初始阶段的形状,n为流变指数,c1和c2为温度指数.γ˙ 为剪切速率,计算如下

剪切速率和温度是影响黏度的两个独立参数.由课题组实验测量与参数拟合获得[33],具体的本构方程参数为 η0=71.217 3 Pa·s,η∞=0.027 1 Pa·s,λ=0.158 2,b=1.381 4,n=0.396 4,c1=-0.01 1,c2=0.061 1.

2.3 流体体积法

两相流问题中,界面的复杂演化是宏观尺度两相流问题的一个主要特征[34].采用VOF 方法来跟踪流体表面.该方法利用流体体积与网格体积的比值来计算VOF 函数的值,该函数通过界面压缩方法保持尖锐的界面,并且在没有重新初始化步骤的情况下保持质量守恒.通过求解VOF 函数所满足的运输方程,可以获得全流场的流体体积函数分布情况,并进而构建运动界面.通过追踪界面,可以获得其附近所有的流场信息.流体运动时,气-液的交界面也变化,所以需要更新每个单元对应的体积函数,相函数的运输方程[35]是VOF 的核心,表达式为

其中,u为速度矢量;α 为整个计算域的相函数,其值在气泡内部为0,在气泡外部为1,在界面处为0～1 之间.下式用于计算气相的局部体积分数

其中,下标s 是网格编号;As是编号为s 的网格单元的面积;ψs是界面追踪的直观指标,同时也是界面构造的关键参数.

此外,还采用PLIC 方法对界面进行重构,通过在单个网格中划分斜线线段来近似两相界面,斜线的斜率通过附近的相分数来确定,具有误差小、精度高的优点.通过求解单个网格内气泡的局部体积分数梯度,可以获得界面的法向量.计算界面法向量的方法如下

在每个网格中,下一时刻气泡的局部体积分数可以通过计算当前时刻网格内气泡的局部体积分数与这段时间流入网格内的气泡体积分数之和来获得.通过更新下一时刻网格内的气泡局部体积分数,就可以对整个流场中的气泡界面进行重构.

3 结果分析和讨论

3.1 不同温度下的气泡运动特性

气泡的运动速度和周围液体的流动状态会影响气液两相之间的传质传热效率[36].气泡的变形程度受到黏性力和表面张力的影响,黏性力或表面张力越大,气泡变形程度越小.研究将体积分数为0.5 的区域定义为气泡区域.图2(a)显示了不同温度下气泡稳定后的轮廓,由于凝胶液体黏度较大,所以本文中所有气泡都没有明显的变形,气泡形状更接近球形.图2(b)和图2(c)显示了不同时刻下气泡的运动轨迹和重心位置,可以看到温度升高会使气泡运动得更远,并在竖直方向基本保持直线运动.气泡的变形是由于气泡的上升过程中,其顶端与底端压力的分布不均导致的.如图2(d)所示,温度升高会增加气泡的变形.由于气泡的形状均表现为椭圆形,因此气泡的变形程度主要表现在纵横比上.纵横比是衡量气泡变形程度的重要参数,其值为气泡最大横向距离与最大纵向距离之比[37].

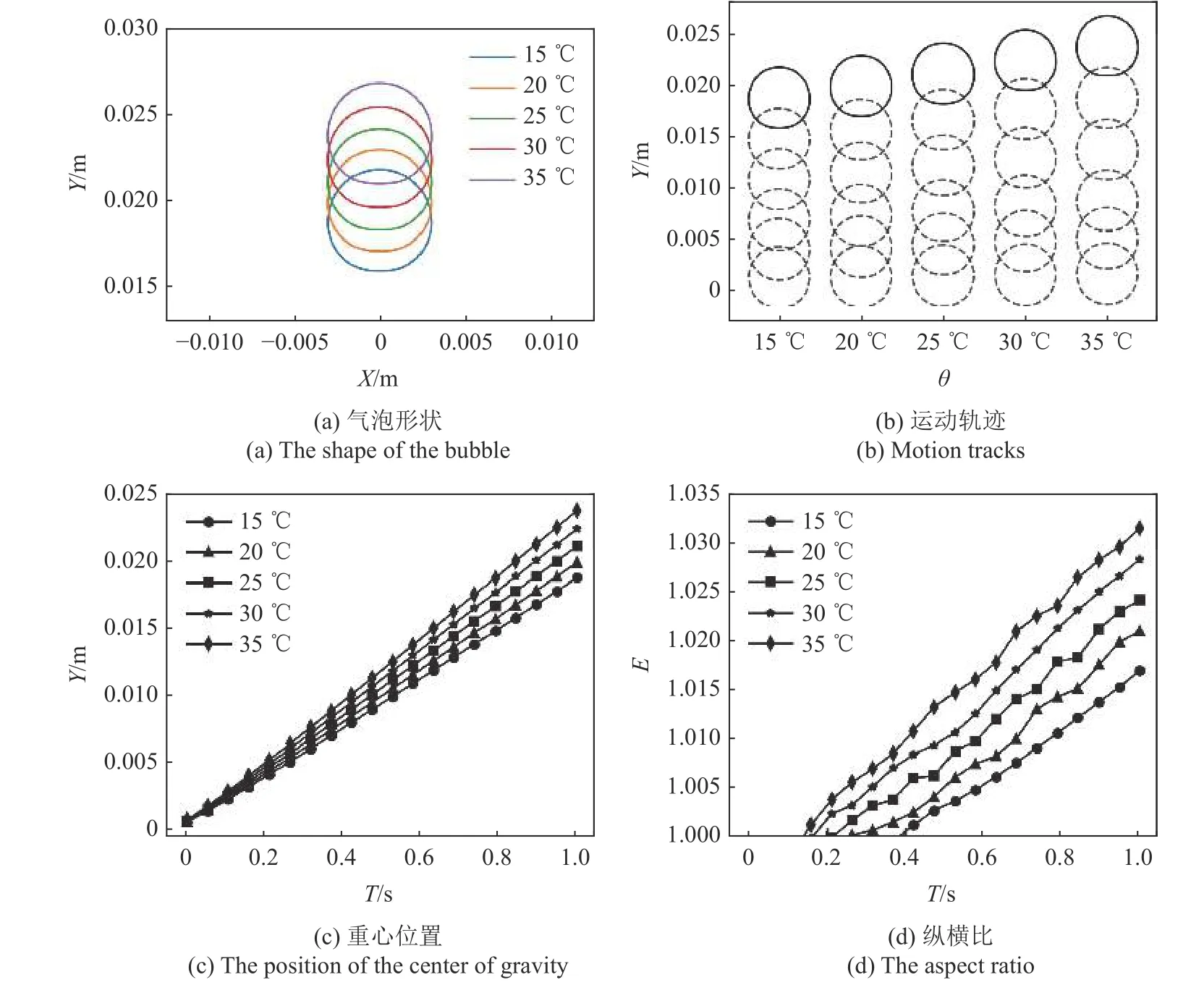
图2 不同温度下气泡的运动情况Fig.2 The movement of bubbles at different temperatures

气泡形状的变化会对气泡的动力学特性产生重要的影响[38],尤其是气泡的尾涡会随气泡形状的变化而不断变化,并最终达到稳定状态.图3 显示了气泡中心参考系下的流线图,展示了气泡的流动情况.气泡的变形会导致流线的不同,可以看到在气泡内部出现两个环流区,而气泡的尾流区没有任何额外的环流区.由于内部环流的惯性作用,环流会被底部表面切为两个部分,即内部环流和外部涡流.由于变形气泡的曲率较小,气泡尾部没有形成尾涡[39].图4展示了不同温度下气泡上升速度的变化情况.气泡上升的初始阶段浮力占主导作用,导致气泡的纵向速度急剧增加[40].随着气泡的不断上升,在高黏度的流体中气泡所受到的阻力逐渐增大,使得气泡上升的加速度变小,直到气泡达到一个稳定状态.此时气泡的速度即为其终端速度.随着温度升高,液相的表观黏度降低,气泡周围液体的阻力也随之降低,导致气泡的终端速度随着温度升高而增加.图4(b)显示了气泡上升速度与纵横比的关系.可以看到气泡的上升速度与纵横比呈正相关.气泡速度[41]的计算公式为

图3 不同温度下气泡周围的流线图Fig.3 Streamline diagram around bubbles at different temperatures

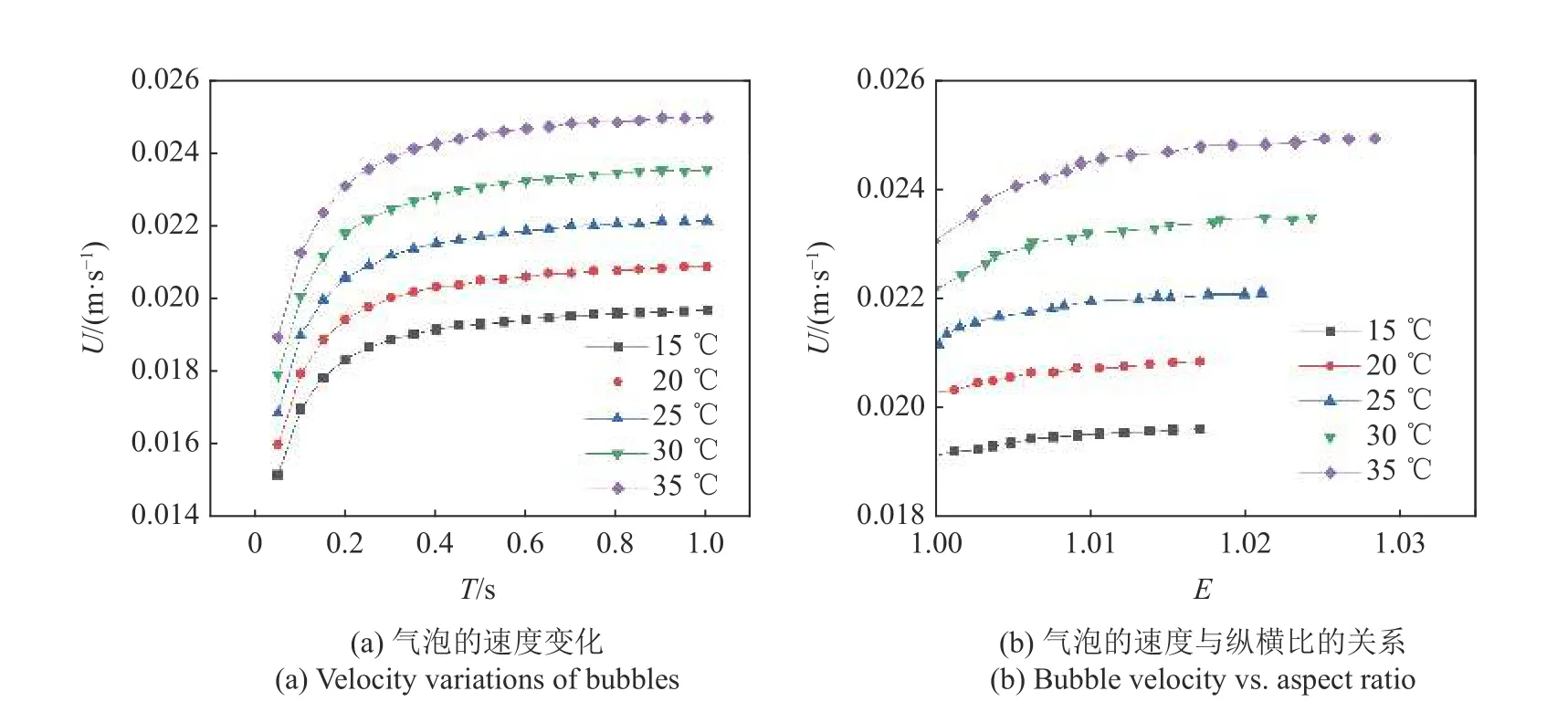
图4 不同温度下气泡的速度与纵横比Fig.4 Velocity and aspect ratio of bubbles at different temperatures

式中,Ω 为气泡区域的面积,u为每个网格上读取的速度.

3.2 不同温度下气泡周围液相黏度及剪切速率分布

由于凝胶流体的黏度较高,气泡在其中运动时轨迹和形状相对稳定,从而容易形成稳定的剪切流场.不同气泡的终端速度差异主要是由于它们受到的阻力不同[42].摩擦阻力与液相的黏度相关,图5 上方显示了气泡周围液相的表观黏度分布情况.为了方便比较,将液相的表观黏度进行了最大值归一化处理,4 条等高线分别为0.98,0.95,0.9 和0.8.剪切速率的增加会降低剪切变稀流体的黏度,因此当气泡上升时,气泡周围的液体黏度会降低,即处于高剪切区.同时,气泡周围液相低表观黏度区的增大会减小气泡上浮过程所受到的摩擦阻力,从而提高气泡的终端速度.

图5 不同温度下液体中的表观黏度(上)和剪切速率(下)Fig.5 Apparent viscosity (top) and shear rate (bottom) in liquids at different temperatures

图5 下方为剪切速率分布的云图,根据图中的分布情况可以看出,在剪切速率较低的区域,液相表观黏度较高,反之则较低.此外,在气泡的赤道处出现了一条腰线,气泡顶部和底部均出现了高剪切速率区,并从气泡上下两部分向外辐射.在腰线处液体的表观黏度最高,剪切速率最低.

3.3 流体性质对气泡运动的影响

当流体的流变指数n=1 时,该流体为牛顿流体,其黏度与剪切速率无关.当n＜ 1 时,流体表现为剪切变稀流体.流变指数n控制黏度随剪切速率快速变化期间的斜率.图6 展示了n=0.2,n=0.4,n=0.6 和n=0.8 这4 种情况下气泡周围液相的表观黏度和剪切速率分布.结果表明,当n值较小时,液相的剪切稀化效应更明显,说明流体更容易流动,气泡周围液体的表观黏度降低,剪切速率增加.

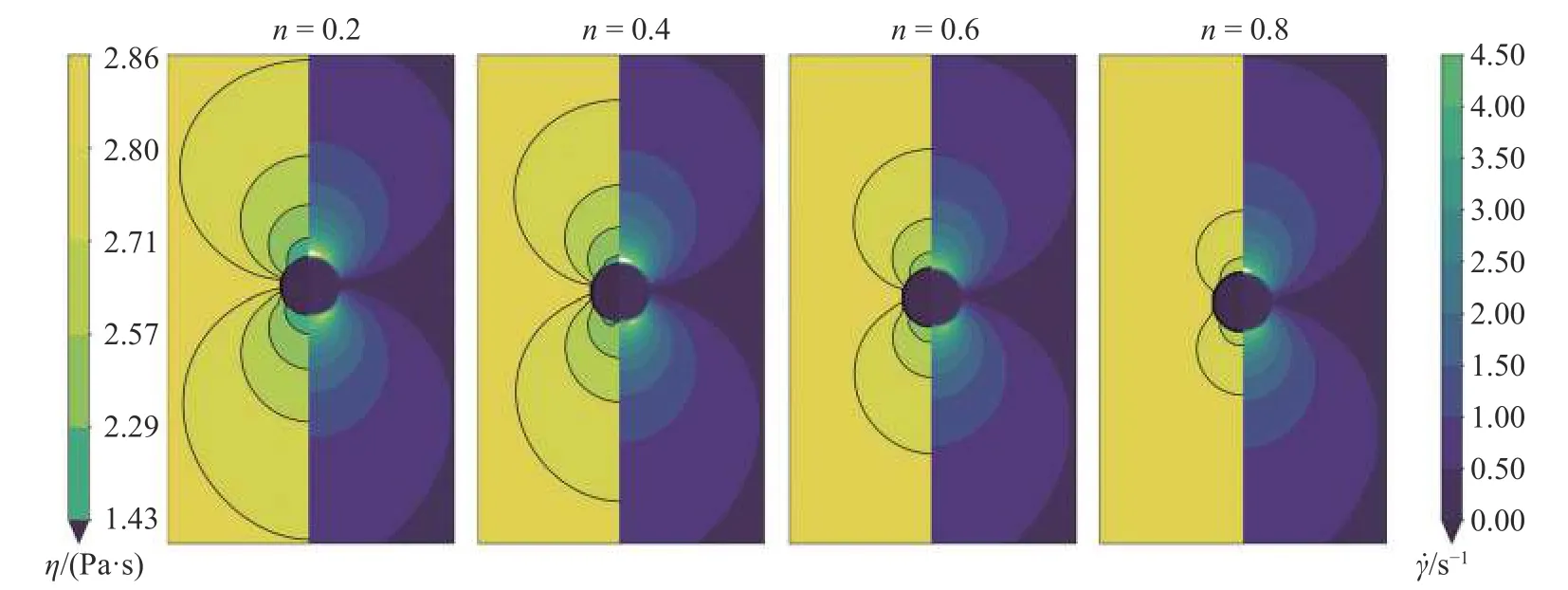
图6 不同流变指数下的表观黏度(左)和剪切速率(右)Fig.6 Apparent viscosity (left) and shear rate (right) at different rheological indices

图7(a)显示了流变指数n对靠近气泡底部的液体黏度的影响.随着流变指数的减小,气泡底部附近的液体黏度下降更多.同时,剪切稀化效应会导致液体的黏度降低,动能耗散减小,从而也会使气泡速度增加.图中还显示了气泡在牛顿流体n=1 中上升的结果.如图7(b)说明了流变指数n对靠近气泡下方的液体速度的影响.越靠近气泡下方液体速度越大,其中由于剪切稀化效应,其值随着流动指数的减小而增加.

图7 流变指数对气泡底部的黏度及速度的影响Fig.7 Effect of rheological index on viscosity and velocity at bubble bottom

当气泡向上运动时,液体被推向气泡的下方,形成一个向下的流动.这个流动使得气泡周围的液体受到强烈的剪切应力,从而引起液体的黏度降低,同时也使液体的流动速度增加.另外,浮力的作用使得气泡周围的液体向外扩散,这进一步降低了液体的黏度.

图8(a)和图8(b)分别显示了在剪切稀化流体中,不同流变指数下气泡纵横比和重心随时间的变化.从图中可以观察到,在剪切稀化效应越明显的流体中,气泡的纵横比变化越小.液体中低表观黏度区的增大是由于剪切稀化效应导致的,这使得气泡受到的黏性阻力减小,其上升速度变快,因此气泡的重心位置也逐渐升高.

图8 流变指数对气泡的纵横比及重心位置的影响Fig.8 Effect of rheological index on the aspect ratio and the position of the center of gravity of bubbles

气泡终端速度会受到液相流体性质的影响,如图9(a)所示,随着时间的推移,气泡速度快速增加并逐渐稳定.在剪切稀化效应较强的流体中,由于流体的剪切作用,气泡周围液相的黏度会大幅下降,从而减小了气泡受到的黏性阻力,因此在剪切稀化液体中气泡更容易上升.气泡的终端速度也越大.

图9 流变指数及特征时间对气泡速度的影响Fig.9 Influence of rheological index and characteristic time on bubble velocity

同时,特征时间λ是描述剪切稀化液体特性的重要参数.当液相受到扰动时,液相中的高分子链受到扰动,平衡态会遭到破坏,特征时间λ是描述液相从非平衡态恢复到平衡态所需要的时间,当λ=0 时,流体为牛顿流体.在本研究中,选择了λ=0.05 s,0.158 2 s,0.25 s,0.5 s,1 s 这5 种情况.从图9(b)可以看出,气泡的终端速度随着λ的增加逐渐增加,在t=0.4 s 之前,气泡终端速度增幅较大,而在t=0.4 s 后,气泡终端速度增幅较小.此外,当特征时间较大时,其对气泡速度的影响也更为明显.

图10 显示了气泡的运动轨迹随着特征时间的增加而变化,气泡在纵向拉长.这是因为特征时间越大,λ越大,液相受到扰动后恢复到平衡态所需的时间越长,剪切稀化效应更强,气泡形状越不稳定,气泡被拉伸和扭曲的程度更高.

图10 不同λ 下的气泡运动轨迹Fig.10 Bubble trajectory under different λ

根据图11(a)和图11(b),可以看到在不同的温度和流变指数下,气泡终端速度和纵横比均有相应的变化.随着液体流变指数的增加,气泡周围的阻力会增加,导致气泡终端速度下降,同时气泡的形变也会增加.此外,如前所述,温度对液体的黏度也会产生影响,从而间接地影响气泡周围的摩擦和阻力大小.因此,随着温度升高,气泡的终端速度也会增大,并且气泡的变形程度也更为明显.在低温下流变指数对气泡纵横比的影响要更小些.

图11 3 种温度下气泡的纵横比和速度随流变指数与特征时间的变化情况Fig.11 Variations of aspect ratio and velocity of bubbles with rheological index and characteristic time at three temperatures

根据图11(c)所示,λ的增加加速了液体从牛顿流体到剪切稀化流体的转变.当温度保持不变时,液体的λ减小会使其黏性下降,气泡周围的液体阻力随之下降,使得气泡的纵横比更大.同时随温度的升高,气泡的纵横比在均匀增加.由图11(d)知气泡的终端速度随着λ 的增加逐渐增加,并且高温能够促进气泡的上升,使得气泡的终端速度增加.随λ的增加,温度对气泡终端速度的影响逐渐变大,气泡速度增加的幅度也随之变大.

在大的Eo数条件下,由于表面张力相对较弱,气泡会具有较大的变形.如图12 所示,在本文研究的Eo=15,100,950 这3 种情况下,随着计算时间的增加,气泡底部继续向上凹陷并向外水平扩展.当表面张力较大时,气泡可以抵抗射流的影响并保持形状稳定,使得射流不会突破气泡边缘,射流在底部界面沿径向方向流动[43].而当表面张力较小时,在气泡内外压力差的作用下,气泡的底部向上凹陷,但并不会在气泡外部形成涡流.