基于DSMC 方法的再入飞行器微烧蚀研究1)

甘 驰 陈 松,2) 张 俊

* (北京航空航天大学中法工程师学院/国际通用工程学院,北京 100191)

† (北京航空航天大学航空科学与工程学院,北京 100191)

引言

飞行器在以高超声速再入大气层时将会产生一道强激波,使得飞行器壁面周围温度急剧升高,导致空气发生振动激发、离解甚至电离等一系列物理化学变化[1].针对这种极端的气动热环境,常常需要进行热防护系统(TPS)设计.相比于可反复使用的热防护系统而言,高超声速条件下更需要烧蚀性的热防护系统.这种烧蚀性TPS 一般是多孔设计,通过材料质量的损失例如热解、氧化和升华等一系列复杂的物理化学反应来为飞行器缓解极端的热载荷.隔热材料热解后产生的气体会沿着材料向外移动到边界层区域,由温度相对较低的热解气体带走部分热量.同时由于TPS 材料的多孔设计,高温的边界层气体也可能会向内流入材料微观结构中,引起更深层次的化学反应,影响结构内部的热流.因此研究局部区域的微烧蚀问题对于整个热防护系统的设计显得十分重要.

当飞行器因强烈气动加热而发生烧蚀时,烧蚀外形的变化会进一步影响流场情况,因此在模拟烧蚀过程时需要进行耦合计算[2].为此,除了进行气动热环境分析外,还需要建立准确的烧蚀模型,以及如何在烧蚀过程中高效地处理烧蚀移动边界的后退问题.Liang 等[3]针对“天宫一号”的再入过程建立了一维烧蚀模型和传热模型;周印佳等[4]采用Sutton-Graves 和Tauber-Sutton 理论计算驻点热流以及Landau 坐标系实现烧蚀动网格,通过求解瞬态有限差分热传导方程实现了烧蚀热防护一体化计算方法;李伟等[5]采用有限体积法建立了碳纤维增强复合材料的微观烧蚀数值模型,并引入了固体相体积分数与界面重构技术;胥建宇[6]提出了基于比色测温的烧蚀模型表面温度测量方法,并建立了基于LSTM神经网络的烧蚀量预测模型;王晓婕[7]组合使用生死单元法、网格自适应技术和网格重划分技术建立了气动热环境-固体导热-烧蚀一体化耦合计算方法;杨凯威等[8]针对有限元软件采用了自编热流加载和烧蚀移动边界用户子程序方法,建立了高速空气舵前缘三维烧蚀和温度场耦合计算方法.

然而,在相当大的高度时,飞行器所处的气体环境十分稀薄,克努森数Kn＞ 0.01,这将使得传统的计算流体方法难以给出准确的模拟结果.在高度不断下降的过程中,虽然飞行器外部周围的流体可能整体上是连续的,但由于材料尺度较小,并且飞行器头部存在各种端口、紧固件等微小粗糙元,局部的克努森数可能仍处于过渡区甚至稀薄区.因此,在这种情况下需要采用适用于稀薄和近连续领域的具有高保真度的气体动力学方法.

直接模拟蒙特卡洛方法(DSMC)于20 世纪60年代由学者Bird 提出[9],从统计学的角度求解玻尔兹曼方程,通过模拟大量微观粒子的运动和碰撞来反映真实的流场情况.DSMC 方法适用于模拟稀薄气体流动,并且发展至今已能够应用于许多领域[10].现有的众多程序都能够很好地实现DSMC 方法,如Bird 开发的代码DS2V[11]和DS3V[12],美国国家航空航天局NASA 开发的代码DAC[13-14],Dietrich 等[15]开发的代码MONACO,Scamlon 等[16-17]开发的并行代码dsmcFoam 等.

近年来,Plimpton 等[18]基于DSMC 方法开发出了开源并行程序SPARTA.SPARTA 采用多层笛卡尔网格对粒子进行分组,能够高效地模拟粒子间的碰撞以及化学反应,同时允许在流体网格中加入固体壁面对象,并模拟粒子与壁面之间的碰撞与反射过程.程序采用了Marching Square 算法来生成以及实时更新烧蚀外形,并记录粒子与壁面碰撞时传递给壁面的能量,模拟烧蚀面吸收的热量来扣除网格的节点值,进而模拟烧蚀过程.该程序能够同时考虑多组分化学反应,具备模拟高超声速化学非平衡流动的能力.流场初始条件以及网格信息通过读取外部输入文件来设置.

随着统一随机粒子(USP)方法的提出,SPARTA还在不断发展之中[19].针对于飞行器头部局部粗糙区域的烧蚀问题,本文采用最新的标准SPARTA 源码,并在此基础上进行了改进.首先对粒子与壁面碰撞时动能的记录规则进行了修改,避免了负能量出现的情况;其次添加了缩放系数使网格节点值与粒子动能值处于同一量级,减少一个烧蚀循环内的溢出损失;最后对程序中烧蚀速率的计算方法进行了改进,以更准确地描述烧蚀物理过程.本文模拟了几种典型几何外形的烧蚀过程,并给出了最终的烧蚀外形以及流场图像.在不考虑转捩现象[20]以及气体离解反应和电离反应的情况下,球锥烧蚀的模拟结果与参考文献[21]的烧蚀结果在驻点线附近取得了较好的一致性,验证了DSMC 方法以及SPARTA 程序对于烧蚀问题研究的可行性.同时,通过斜楔体的烧蚀计算本文对带有微小粗糙元的飞行器表面的烧蚀问题进行了探讨.如何将更加复杂的因素加入到程序中从而给出更加准确的烧蚀计算结果也是今后主要的研究方向.

1 研究方法

1.1 分子动理论与DSMC 方法

分子动理论是物理学中研究物质微观粒子运动行为的理论.该理论认为分子的运动是随机的,并遵循牛顿力学和统计物理学的原理.所有微观分子的运动和相互作用共同影响了气体的宏观性质,例如密度、温度和压强等性质.当气体密度很低时,分子平均自由程远大于分子自身的尺寸,连续介质假设失效,此时的气体被称之为稀薄气体.在稀薄气体领域,分子间的相互作用可以忽略不计,分子个体的行为所产生的影响更加显著.在这种情况下,分子被认为是非常小的硬球,其主要行为包括平动和碰撞.分子在平均自由程内可视为作直线运动.

稀薄气体动力学的核心是玻尔兹曼方程.该方程描述了分子在流场中的运动和碰撞.然而由于玻尔兹曼方程形式复杂,直接求解相当困难.因此,许多数值模拟方法被发展出来用以求解稀薄气体问题.其中最常用的方法是DSMC 方法.

DSMC 方法是基于统计物理学的数值模拟方法,最初被用来模拟稀薄气体的动力学行为,经过数十年的发展已经在烧蚀问题以及与流场的耦合计算等研究中具有重要作用.在该方法中,每个模拟粒子代表了大量相同的真实气体分子.粒子的运动和碰撞在一个时间步内可认为是解耦的.粒子在该步长下沿直线运动,并被随机选取来模拟分子间的碰撞.常用的分子碰撞模型有VHS 模型、VSS 模型.此外,碰撞过程中的化学反应由热化学模型来模拟,例如TCE 模型和QK 模型等.在烧蚀问题中,粒子会与固体表面发生碰撞并反射或被吸收从而反映气-固间的相互作用过程.

1.2 SPARTA 程序

SPARTA 是基于DSMC 方法的开源并行程序,其运行效率高,用户可以方便地添加新功能.该程序中的对象可分为3 类: 模拟粒子(simulated particles)、计算网格(grid cells) 以及流体中的壁面(surface elements).计算网格始终是结构化网格,可用于二维和三维流动的模拟.在二维流动中,网格为与两条轴相互平行的矩形,壁面外形由数个点两两连接而成的线段组成;而在三维流动中,网格则为长方体形状,壁面由众多点三三连接形成的三角形组成.此外,网格可以根据需要进行多层加密,以及在不同区域进行不同程度的加密.

SPARTA 的输入文件包括了许多计算参数的设置,例如计算域大小、网格尺寸、来流条件、采样设置以及需要计算的流体性质等.在流场中,粒子的性质也需要进行设置,如粒子的质量、转动自由度、振动自由度等.SPARTA 使用VHS 或VSS 等碰撞模型来模拟粒子之间的相互作用.用于烧蚀的隐式壁面(implicit surface)信息由二进制文件存储.

SPARTA 工作流程示意图如图1 所示.在开始计算过程之后,程序首先会将输入文件中的命令全部读入,之后再开始执行相应的命令.程序会根据输入的网格信息自动生成结构化网格并初始化.接着,程序会在指定的边界处生成模拟粒子并为其赋予初始速度等信息,然后按照该速度来移动粒子.在每个时间步内,计算域外的粒子会被移除,而与壁面碰撞的粒子会发生反射或被吸收.此外,程序会随机选取粒子对并模拟碰撞过程,碰撞后粒子的速度会发生改变.循环内程序会每隔一定时间步进行采样并在循环的最后输出计算结果,如包括粒子和壁面在内的流场图像、每个网格的坐标以及网格内流场的温度、压强、密度等信息.在输入文件中会规定总共模拟的步数Ntotal,如果当前模拟步数N达到了总共的模拟步数Ntotal,程序就会停止运算.

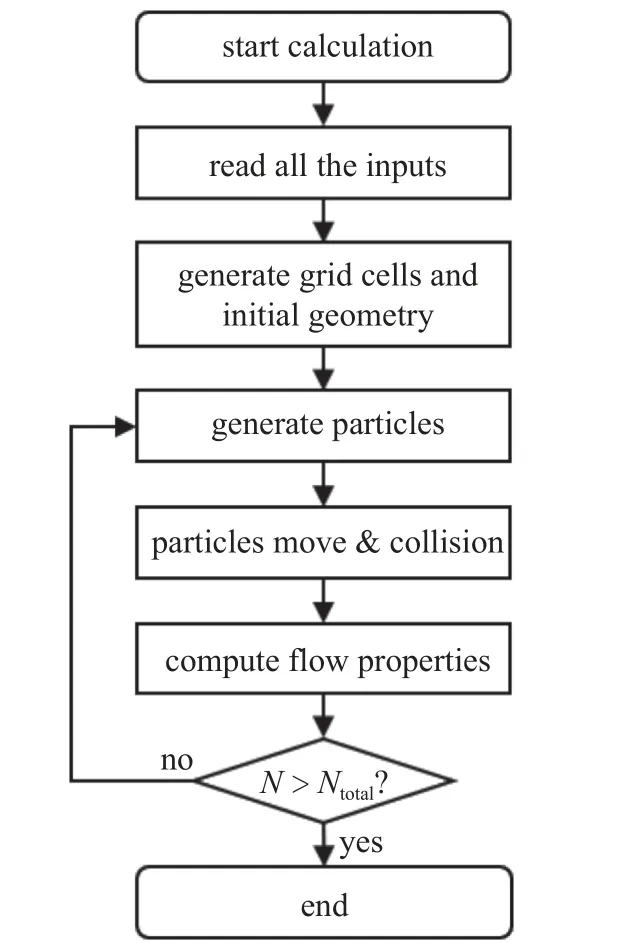
图1 SPARTA 基本工作流程图Fig.1 The basic flowchart of SPARTA

1.3 烧蚀模型

目前,计算烧蚀速率的方法主要包括解析烧蚀外形方程[2]、求解烧蚀边界热平衡方程[3,22-23]、采用气动热化学烧蚀方法[24-26]等.SPARTA 采用类似于热平衡边界假设的烧蚀原理,认为气动加热量与烧蚀吸热量达到平衡.

SPARTA 采用Marching Square 算法对烧蚀后的壁面外形进行实时更新.该算法与Marching cubes 方法类似,能够根据输入的二维标量场生成云图或等值线.该算法一般用于作地形图上的等高线或者气象图中的等压线,而在SPARTA 中用于生成烧蚀外形.算法的输入可以看作是一个二维矩阵,矩阵中的每一个元素是一个节点,4 个节点可以连接形成一个矩形,相当于一个计算网格.因此每个网格都具有4 个节点值.通常情况下,该算法会被给定一个阈值,大于该阈值的节点值被视为1,小于则视为0,因此每个网格的4 个节点分别可能为0 或者1,总共有16 种不同的情况.对应这16 种情况,算法给定一张查找表,不同的情况下网格会有不同的线段几何外形,并且每个网格一定能在该索引表中寻找到相应的线段几何外形,如图2 所示.

图2 Marching Square 算法的填充规则Fig.2 Look up table of Marching Square algorithm

Marching Square 算法的基本步骤如下:

(1) 遍历每一个网格,获取其4 个节点的数值;

(2) 根据节点数值的分布情况确定该网格对应的索引值,采用二进制编码的方式,将4 个节点的数值映射到一个4 位二进制数上,例如0000,0001,0010 等;

(3) 利用预先建立的查找表,在查找表中找到对应的线段几何外形,例如水平线段、垂直线段和斜线段等;

(4) 最终将所有网格的线段合并起来构成整体壁面外形.

在SPARTA 中,被线段所围的区域被视为烧蚀体,能够与模拟粒子发生碰撞并烧蚀.主程序根据输入条件如计算域尺寸、网格尺寸和加密信息等自动生成结构化隐式网格.其中每个网格为正方形(二维计算)或立方体(三维计算),每个二维正方形网格具有4 个节点,三维立方体网格具有8 个节点.在给定阈值之后,根据每个网格的4 个节点值,使用Marching Square 算法高效地划分出壁面外形.以二维计算为例,初始烧蚀外形的生成如图3 所示.该算法能够根据实时的节点数值信息来高效地更新烧蚀外形.

图3 SPARTA 烧蚀外形划分示意图Fig.3 The schematic of how SPARTA generates ablation geometry

在整个烧蚀模拟的过程中,模拟粒子不断地在来流边界生成并以指定的速度进行运动.在每一个时间步内,粒子进行直线运动或与其他粒子发生碰撞.同时部分粒子可能会与烧蚀壁面发生碰撞并依据壁面的温度以一定的速度发生漫反射或镜面反射.因此在每一时间步内,烧蚀外形上的不同部分会经受不同程度的粒子碰撞,对应于不同程度的气动热环境.SPARTA 会记录下每个烧蚀循环内每一时间步内壁面上发生碰撞的信息,例如与粒子发生碰撞的次数,粒子碰撞前后的速度、动量等,并根据记录下来的物理量对壁面进行烧蚀,例如计算粒子传递给壁面的总动能

此外,SPARTA 的烧蚀外形变化是在每次烧蚀循环后进行更新的,而每一个烧蚀循环由若干时间步组成.SPARTA 烧蚀循环流程图如图4 所示.图4中N为当前模拟步数,Nac为一个烧蚀循环所包含的模拟步数,k为正整数.以使用粒子动能变化作为烧蚀判据为例,每一个时间步内粒子传递给壁面的动能都会被记录下来,直到该烧蚀循环结束.烧蚀循环结束时,每一个壁面单元所吸收的能量将会被累加起来形成一个“烧蚀量”.程序会读取该壁面单元所在网格的4 个节点值,从节点值中扣除该“烧蚀量”.在该烧蚀循环的最后,程序会根据更新后的节点值来生成新的烧蚀外形.例如当烧蚀循环步数Nac为100 时,每100 个时间步内壁面外形的“耐久值”都在不断减小,最后在第100 步时壁面外形会被更新.SPARTA 会将动能值转化成与节点值相当量级的数值并从对应的网格节点值中扣除,直至该节点值为0,然后从该网格的其他节点值中继续进行扣除.当一个网格的4 个节点值均为0 后,该网格内的壁面单元即为“完全烧蚀”,此时该网格中不再存在壁面单元,粒子则可以进入该网格与“更里面”的壁面再次发生碰撞,并将该过程循环下去直至计算结束.因此在每一个烧蚀循环内,计算网格中节点值的分布会不断发生变动,在循环结束时对壁面的外形进行更新.图5 为SPARTA 模拟烧蚀过程的示意图.

图4 SPARTA 烧蚀循环示意图Fig.4 Flowchart of ablation cycle in SPARTA

图5 SPARTA 模拟烧蚀过程示意图Fig.5 Simulated ablation process of SPARTA

图5 中,左侧为初始的壁面外形,其内部的节点值均大于阈值,程序根据Marching Square 算法生成了该近似于正方形的外形.经过一个烧蚀循环后,每个壁面单元经受了不同程度的粒子碰撞,受到了不同程度的气动加热,因此节点值分布发生了变化,如图5 右侧所示.程序会依照新的网格节点值更新烧蚀后的壁面外形,并将该循环继续进行下去.在SPARTA 的烧蚀循环中,最外层的壁面单元总是会最先被烧蚀.并且粒子碰撞最频繁、碰撞粒子动能最高的区域烧蚀量最大,以此来反映真实、物理的烧蚀过程.

在SPARTA 中,粒子与壁面碰撞后反射的速度由基于壁面温度的分布函数给出.在这种条件下,温度较高的区域粒子反射的速度较大,传递给壁面的能量较小,因此反而烧蚀的速率较慢,与真实的情况相背;甚至当壁面温度较高时,可能会出现碰撞后速度大于碰撞前的情况,该能量值成为负数.因此本文对此项进行了优化,将式(1)中碰撞后的动能项舍弃,只考虑入射的速度,从而保证温度越高的区域烧蚀速率越快.

另外,由于SPARTA 中烧蚀外形的更新是在每次烧蚀循环结束之后进行,因此每个循环内只有最外层的网格承受热量,而内层的网格并不会被烧蚀.在某些情况下,粒子传递给外层网格的能量可能足以在循环结束前烧蚀掉外层网格.然而,由于外形没有及时更新,最外层的网格仍会存在并继续与粒子碰撞.在这种情况下,本应烧蚀内层网格的能量在烧蚀实际并不存在的外层网格.为了解决这个问题,本文在记录能量时添加了一个缩放系数 α,以确保在一个烧蚀循环内无法完全烧蚀掉一个完整的网格,从而减少能量溢出的损失[27]

式中,fnum为真实分子与模拟粒子的比值,即一个模拟粒子代表多少真实的分子;Acell为网格的尺寸,如二维方形网格的边长;dt为时间步长;Emax为模拟粒子最高的动能.

此外,当前模拟中计算网格的尺寸会影响烧蚀速率.fnum中真实分子的数量与气体的数密度有关,如下式所示

为了保证计算效率,每个网格单元中模拟粒子的数目npercell通常是个定值.如果其值过大,模拟过程将耗费大量时间;而如果太小,DSMC 方法的统计特性将会引起较大的误差.另外,在同一算例中,体积数密度 ρnum始终保持不变.在二维条件下,沿z方向的网格单元长度lz也是常数,可以忽略.因此,fnum与x和y方向的网格单元大小lx和ly的乘积有关.通过代入和简化,并假设用k表示其中的常数项,则式(1)中的系数 β 变为

因此,β 正比于lx和ly的乘积与壁面元素长度a的比值.而a的大小与网格尺寸非常接近,因此lx和a可以同时消去,还剩下ly.这表明烧蚀速率实际上受到网格尺寸的影响.较大的网格意味着更快的烧蚀速率,而较小的网格则会导致较慢的烧蚀速率.烧蚀过程本身的速率受到了模拟参数的影响,将会产生误差.

为了解决这一问题,对于二维模拟,系数 β 的分母被修改为了a2.修改后保证了烧蚀速率不再受网格单元大小所影响,而是取决于烧蚀过程本身.

由于SPARTA 程序受到文件数据格式的限制,此前节点最大值被设定为255.为了考虑材料的传热特性,本文采用一维热传导方程以及烧蚀表面的热平衡方程计算烧蚀速率[3].在烧蚀表面的热交换过程包括高超声速来流的气动加热热流qaero、材料结构吸热热流qcond以及烧蚀表面的辐射热流qrad

在DSMC 方法中,气动加热是由粒子与壁面碰撞前后传递的动能所实现的,因此气动加热热流为粒子传递的动能流量之和

烧蚀表面的辐射热流与壁面的温度相关

其中 σ 为Stephan-Boltzmann 常数,其值为 5.67×10-8W/(m2·K4);ε 为发射率,介于0～1 之间.当壁面的温度到达最高点后,结构通过热传导方式所吸收的热量可以认为完全用于结构的烧蚀,即

式中,V为烧蚀表面的后退速率,Q为壁面单位质量的材料烧蚀时所吸收的热量.因此通过烧蚀表面的热平衡方程可以求出烧蚀进行的速率V为

在以Marching Square 算法实现的烧蚀问题中,网格的节点值G将根据该烧蚀速率来设置

以此来实现更加物理的烧蚀过程.

2 典型外形烧蚀模拟

2.1 二维方柱烧蚀模拟

基于SPARTA 的烧蚀模型,本文就一些简单的外形进行了烧蚀模拟.表1 展示了来流条件以及SPARTA 中的网格尺寸、时间步长等条件.

表1 SPARTA 计算参数Table 1 Simulation parameters in SPARTA

烧蚀材料采用典型的碳/碳复合材料的性能参数,其密度为1800 kg/m3,表面发射率为0.8.材料在高空稀薄大气环境下发生化学烧蚀,大气的组成为77% 的N2和23% 的O2,反应体系中包括碳的燃烧、碳氮反应以及碳的升华等反应,在该计算条件下Q=36.95 MJ/kg.来流的气动加热热流qaero由SPARTA 计算得到,在该条件下驻点处的气动加热热流为6.586 MW/m2,除去热辐射所耗散热流后,剩余的热量完全用于材料结构的烧蚀,由此可以计算出烧蚀速率约为0.098 3 mm/s,以及网格的节点数值,最后对SPARTA 的烧蚀过程进行“标定”.

SPARTA 输出了整个烧蚀过程中烧蚀外形的变化图6 和某一时刻流场的速度分布图7.高超声速来流会在方柱前方形成脱体弓形激波,激波正后方温度急剧上升.

图6 二维方柱烧蚀过程Fig.6 The ablation process of the rectangular cylinder

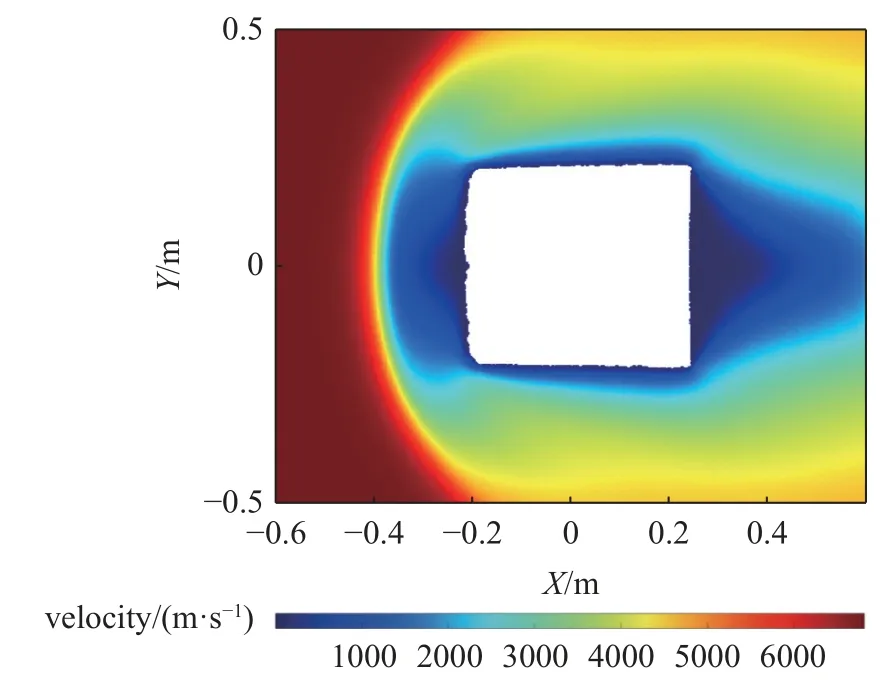
图7 二维方柱绕流速度场云图Fig.7 The velocity contour of the rectangular cylinder

在速度分布图中,方柱前缘有较大一块区域内粒子速度明显较低,而模拟粒子在方柱的棱角处的平均速度要高于前缘中心附近.因此棱角处表现出的平均温度更高,烧蚀后退位移多于前缘中心,前缘将会逐渐烧蚀成弧形.与方柱侧边和后缘碰撞的粒子数量远小于前缘与棱角,并且碰撞时的入射速度较小,所以靠近后缘处的烧蚀量较少,基本维持着原来的外形.根据烧蚀外形的变化图6 可以发现,烧蚀过程与速度场云图所展示的情况基本符合,方柱截面逐渐变成了“子弹”形状,前缘形成了圆弧形状,反映了SPARTA 烧蚀模型的有效性.

2.2 二维圆柱烧蚀模拟

本文同时模拟了二维圆柱的烧蚀,其计算参数与方柱烧蚀相同.在圆柱烧蚀模拟中激波的形状更加贴近前缘圆弧形,因此圆柱表面的温度分布更加均匀.圆柱前缘驻点处承受的温度最高,并且沿着两侧弧形温度逐渐下降.肩部的温度要低于头部驻点,所以在圆柱表面上头部驻点处的烧蚀量最大,离驻点越远的地方烧蚀量越小,整体的烧蚀外形表现出弧形逐渐“变平”的特征.图8 所展示的白色区域为圆柱截面的外形变化.图9 展示了烧蚀过程中某一时刻的温度场分布情况.

图8 二维圆柱烧蚀过程Fig.8 The ablation of the two-dimensional cylinder

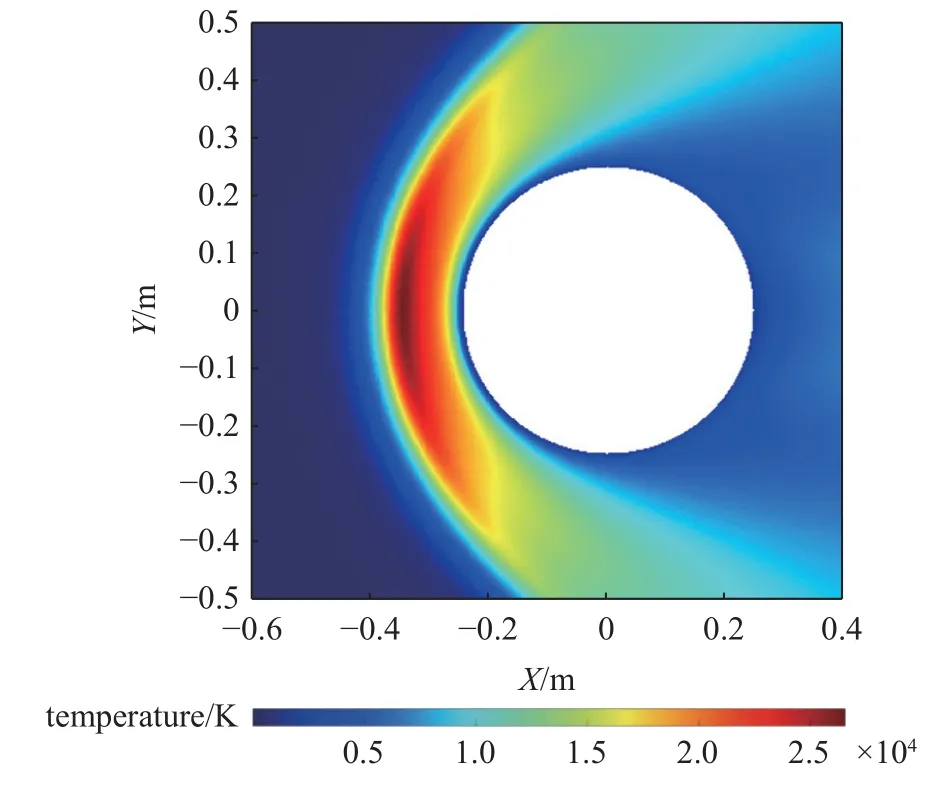
图9 二维圆柱绕流温度场云图Fig.9 The temperature contour of the two-dimensional cylinder

在不考虑化学反应以及电离、离解反应的情况下,激波后驻点线上的最高温度达到了25 000 K.前缘表面上的温度远高于侧后方,因此在整个过程中后退位移要远多于侧后方,使得圆柱的前缘表面呈现明显的扁平形状,而后缘表面仍基本保持圆弧形状.图8 的烧蚀结果和温度场的结果基本吻合.

2.3 二维球锥烧蚀模拟

本文就典型的球锥气动外形[21,28]的高超声速再入过程进行了模拟.该球锥头的截面外形的头部半径为0.032 m,锥角9.8°,其示意图如图10 所示.因为球锥的外形为三维轴对称外形,因此在模拟过程中选取其中一个对称截面进行计算.球锥头从70 km 高度的轨道以5800 m/s 的速度再入大气层.在该高度下,大气的密度为8.3×10-5kg/m3,气体十分稀薄,DSMC 方法能够很好地适用.表2 给出了模拟再入时的稀薄气体环境条件以及SPARTA 模拟时的计算网格设置.

表2 来流条件以及SPARTA 设置Table 2 Free stream conditions and SPARTA parameters of the simulated blunt cone

图10 球锥截面气动外形Fig.10 Aerodynamics geometry of the blunt cone section

由于选取的球锥外形的尺寸较小,相应地,为保证计算的准确度,网格尺寸设置得足够小,并且小于分子的平均自由程;时间步长的选取同样小于分子平均自由时间.壁面采用恒温条件,在烧蚀过程中壁面的平均温度可达到4000 K 左右,因此认为在烧蚀过程中壁面温度保持在该水平上.来流的气动加热热流最高为126.009 MW/m2,此时沿驻点线的烧蚀速率约为1.72 mm/s.

烧蚀过程中某时刻的温度云图如图11 所示.SPARTA 计算的最终烧蚀外形以及参考文献[21]中的原始外形和烧蚀外形由图12 给出.烧蚀过程中初步考虑了O2,N2,O,N,NO 五组分的化学反应.不过图11 的结果中显示的温度最高达到了14 000 K以上,事实上在该温度下气体已经发生了电离和离解反应,反应过程会吸收很大一部分热量,因此真实情况下的最高温度将低于14 000 K.

图11 球锥截面烧蚀温度场云图Fig.11 The temperature contour of the ablated blunt cone section

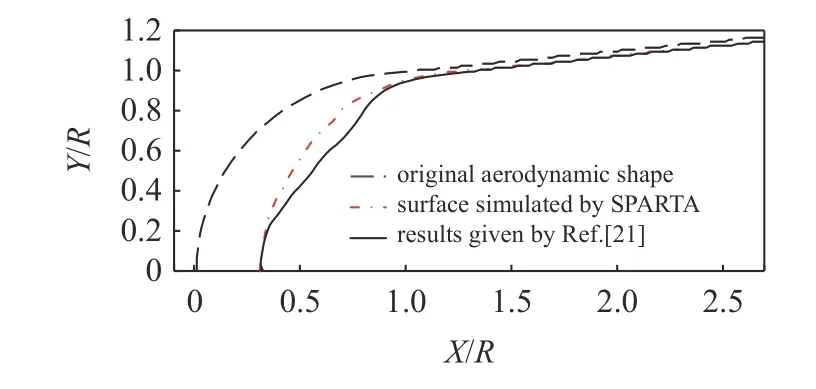
图12 SPARTA 预测烧蚀外形与文献[21]结果对比Fig.12 The surface recession predicted by SPARTA and the comparison with the result in Ref.[21]

由图12 可以看出,在头部驻点线附近,SPARTA模拟得到的烧蚀外形与参考文献结果相符,驻点后退量为9.50 mm,而文献中的烧蚀后退量为9.79 mm,误差在3%以内.在再入过程中,球锥前方形成了弓形脱体激波,激波后头部承受的热流最大,因此烧蚀量最大.肩部区域所承受的热流低于头部区域,因此烧蚀后退位移少于头部.对比参考文献中的烧蚀外形,SPARTA 计算的烧蚀外形整体呈现较为平滑的弧线型,而文献中的结果在肩部附近呈现“削平”的状态.本文结果中肩部区域的烧蚀量明显较少,这是由于参考文献中考虑了转捩现象的影响.肩部的转捩点后的热流会迅速升高,局部的烧蚀量较大,因此肩部区域会产生凹陷.并且由于外形的变化,转捩点不断沿肩部移动,使得整个肩部区域的烧蚀量要多于不考虑转捩现象的情况,导致外形越来越尖.所以SPARTA 计算的外形仍呈圆弧形,而参考文献为典型的“双锥形”.SPARTA 计算中暂未考虑转捩现象的影响,因此导致了部分误差.如何将复杂的转捩机制加入SPARTA 程序中也是今后的改进之处.

3 带有微小粗糙元的二维斜楔体烧蚀模拟

本文模拟了二维条件下带有微小的方块状粗糙元的斜楔体烧蚀[29],其截面几何外形如图13 所示.

图13 斜楔体截面外形示意图Fig.13 Geometry of the wedge with an obstacle

相对于整个斜楔体而言,方块状粗糙元的尺寸非常小,可以视作飞行器表面上的螺栓等小零件.来流条件参考NASA 于2008 年的一项实验数据[29]给出.具体的计算参数如表3 所示,

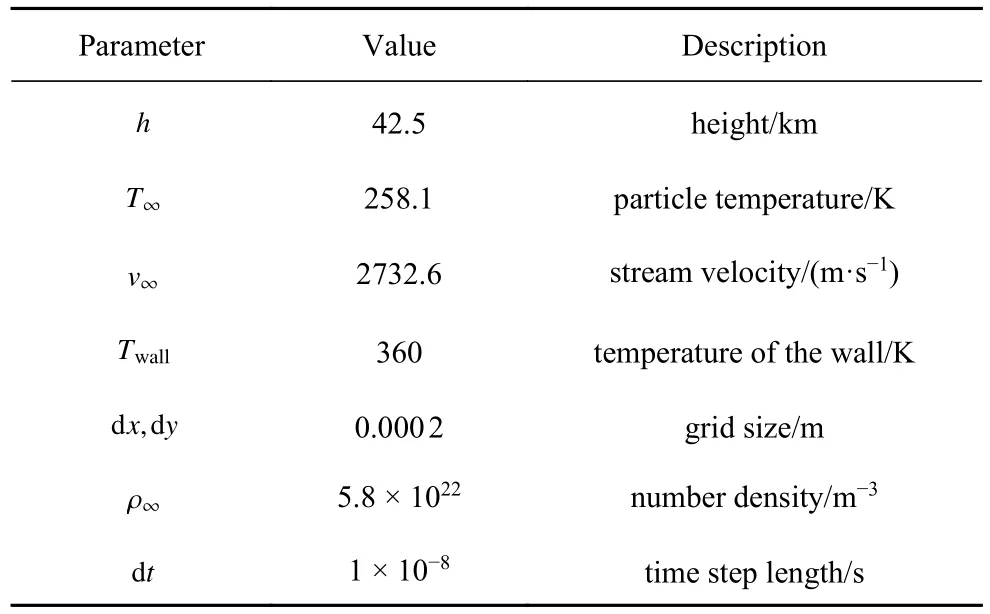
表3 来流条件以及SPARTA 设置Table 3 Free stream conditions and SPARTA parameters of the simulated wedge

为了还原该几何外形,保证微小粗糙元能够以较好的分辨率重现在SPARTA 中,并综合计算量的考虑,网格的尺寸设置为0.000 2 m.相应地,时间步长为1×10-8s.壁面的初始温度设置为360 K.计算中考虑了高温条件下大气组分中N2,O2,N,O,NO五组分的化学反应.而化学烧蚀模型考虑碳的氧化、碳氮反应以及碳的升华反应.在42.5 km 的高度下,大气的稀薄程度有所降低,此时单位质量的烧蚀材料完全熔化时所吸收的热量Q取值为10.20 MJ/kg.驻点处的热流为5.37 MW/m2,烧蚀速率约为0.081 mm/s.

通过初步的分析,斜楔体的头部较为尖锐,来流在前方形成脱体弓形激波,头部会承受较高的热流.同时微小粗糙元附近也会形成局部的高热流区域,因此烧蚀会首先发生在头部以及粗糙元区域.SPARTA计算结果如图14～图16 所示,图14 呈现了烧蚀过程中微小粗糙元的外形变化,图15 和图16 分别展示了流场中温度和克努森数的分布情况.

图14 带有局部粗糙元的斜楔体烧蚀过程Fig.14 The ablation process of the obstacle on the wedge

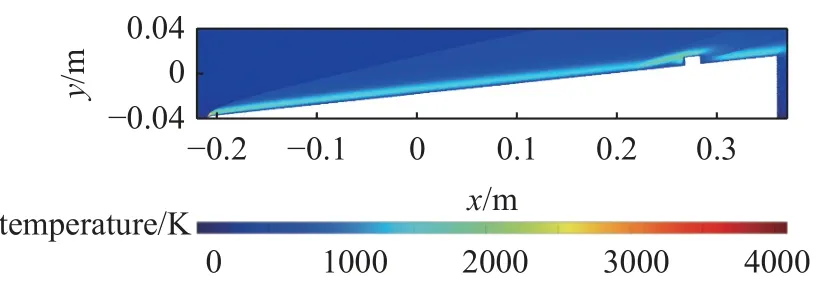
图15 带有局部粗糙元的斜楔体温度场云图Fig.15 The temperature contour of the wedge with an obstacle

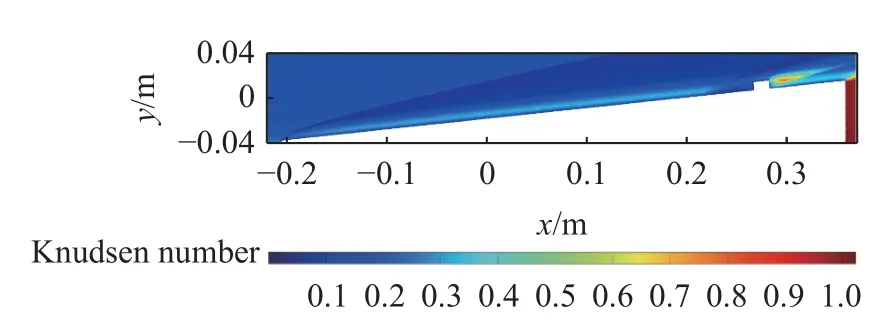
图16 带有局部粗糙元的斜楔体克努森数云图Fig.16 The Knudsen number contour of the wedge with an obstacle

图14 中粗糙元区域的外形变化非常明显,烧蚀开始后左上角迅速变成了圆弧形,并且粗糙元前方的角区开始向内凹陷;然后粗糙元逐渐被削平,前方凹陷的部分也逐渐加深;最后整个粗糙元几乎完全被烧蚀,和斜楔体表面共同后退.

通过温度场云图15 可以看出,斜楔体头部和粗糙元前方温度较高,最高温度达到了3800 K.高温区域主要分布在斜楔的头部区域以及方块状粗糙元的前缘区域.温度场的分布情况表明主要烧蚀的区域集中在头部和粗糙元前缘区域.

图16 为流场中克努森数的分布.通常情况下,当克努森数大于0.05 时,流体的连续介质假设将会失效,此时基于该假设的数值方法也不再适用[30].从图16 可以看出,尽管云图中有部分噪声,但是绝大部分区域的克努森数均在0.1 以上.特别是在粗糙元区域后方以及靠近斜楔表面的区域,克努森数已经远超连续流体的范畴.由此可见,在42.5 km 的高度下,即使飞行器周围所处的流体环境可能是整体上连续的,但靠近飞行器表面的流场仍处于过渡区甚至是稀薄区.因此,DSMC 方法在该情况下依旧是重要的研究方法.

从该算例也可以反映出,飞行器头部表面局部粗糙区域容易先于其他部分发生烧蚀.在飞行器头部布置相关的部件导致形成类似于该粗糙元形状的区域时,需要特别注意该部分的热防护系统设计.

4 结论

本文采用基于分子动理论的DSMC 方法对高超声速飞行器再入过程中的微烧蚀问题展开了研究,针对多种典型气动外形进行了烧蚀计算与分析,并总结了飞行器表面微烧蚀的主要特征.

首先,本文定性分析了二维条件下方柱和圆柱的烧蚀.通常情况下,驻点处的温度最高,因此烧蚀量也会最大.而模拟结果显示,局部尖锐或粗糙的区域热流会更加集中,具有更快的烧蚀速率.

其次,本文模拟了二维条件下典型轴对称球锥的再入烧蚀.在目前设置条件下,计算得到的驻点附近烧蚀速率与文献结果基本相符.不过由于未考虑转捩现象以及复杂化学反应的影响,本文预测的烧蚀量产生了部分误差,结果中激波后温度也偏高.因此如何在程序中综合考虑转捩现象、电离以及离解反应的影响也是重要的改进方向.

最后,本文模拟了二维条件下带有微小粗糙元的斜楔体的烧蚀过程.粗糙元附近存在有相当稀薄的流场区域,表明了DSMC 方法在微烧蚀问题中的重要意义.整个斜楔体的头部以及粗糙元前方热流较高,率先发生烧蚀,粗糙元区域会逐渐被削平并形成凹陷.因此热防护系统的设计要考虑到局部的粗糙元,尤其是飞行器头部较为重要的部件.

本文初步验证了DSMC 方法对于飞行器再入过程中烧蚀问题研究的可行性.此外,Marching Square 算法能够非常高效地更新烧蚀外形,与基于粒子模拟的DSMC 方法契合较好,在烧蚀耦合计算方面具有很大的潜力.在本文微烧蚀研究的基础上,可以预测高超声速飞行器再入过程中的烧蚀速率,为飞行器热防护系统的设计提供理论基础或者为在轨航天器退役后遗骸的再入烧蚀问题提供处理方案.不过本文目前的计算方法仍存在一定误差,并且未考虑到更为复杂的化学反应体系.将以上属性加入到烧蚀模拟中将成为本文接下来的主要工作方向.