基于可变马赫数锥形流场的定平面形状乘波体设计方法研究1)

2023-10-29孟旭飞刘传振

力学学报 2023年9期

孟旭飞白鹏刘传振

(中国航天空气动力技术研究院,北京 100074)

引言

随着宽速域高超声速飞行器的发展,最近十几年,宽速域乘波体一直是乘波体领域的研究热点[1].不过人们提出的很多宽速域乘波体,比如串联式乘波体[2]、并联式乘波体[3]和可变形乘波体[4-5]等,大都是针对乘波曲面的改进,难以兼顾亚声速性能.针对这一问题,有学者提出了定平面形状乘波体概念,这类外形在高超声速阶段保持乘波效应,低速阶段通过合理的平面形状兼顾亚声速性能[6-7],引起了人们的特别关注.当前研究最多的定平面形状乘波体来源于密切锥方法[8],本文作者在之前的工作中推导了密切锥方法中设计曲线与平面形状之间的设计几何关系式[9],设计得到了单后掠[10]、双后掠[11]和“S”前缘[12]等乘波体,大大提升了密切锥方法的灵活性.

不过,基于密切锥的定平面形状乘波体,在不同密切面内使用相同的锥形流,限制了设计空间,而且这种方法被认为没有改善高超声速阶段的宽速域特性[13].近几年有学者提出在不同密切面内使用不同的锥形流场,以扩大设计空间,同时提高宽速域性能.2018 年,在Liu 等[14]的工作中,不同的密切面内锥形流的马赫数相同,但通过改变半锥角使激波角符合一定的变化规律,比如按抛物线型分布.在激波角从对称面处沿展向向外侧增大的流场中,生成的乘波体具有更大的容积,但升阻比较低;与之相反,当激波角从对称面处向外侧减小时,具有更小的容积和更高的升阻比.2018 年,Zhao 等[15]提出在不同密切面内布置马赫数不同、半锥角相同的锥形流,但激波角不同,他们发现生成的外形可以提高升阻比,同时认为宽速域表现提高.2019 年,在Liu 等[16]发表的论文中,不同密切面内锥形流场的马赫数不同,半锥角也不同,但通过调整马赫数和半锥角保证激波角相同,他们认为这种方法生成的外形也具有良好的宽速域升阻比.

基于密切锥的定平面形状乘波体设计,其理论推导有两个前提: (1)激波为直线型;(2)不同密切面内基准流场的激波角相同.原则上说,只要满足这两个前提,即可给定平面形状设计乘波体,不必局限为不同密切面内使用相同的锥形流场.因此本文结合定平面形状乘波体概念和可变马赫数流场[14]的思路,在不同密切面内使用马赫数不同但激波角相同的流场,开展基于可变马赫数流场的定平面形状乘波体设计,扩大设计空间,并与使用固定锥形流场的乘波体作比较,探索定平面形状乘波体在高超声速范围内的宽速域特性.

1 设计方法

1.1 基于可变马赫数流场的密切锥方法

密切锥设计方法由给定的激波出口形状拟合流场,进而生成乘波体外形.在密切锥方法中,有两条设计曲线,一条是激波出口型线(inlet capture curve,ICC),决定了激波的出口形状;另一条为流线追踪起始线(flow capture tube,FCT),表示流线追踪的起始投影线.

密切锥乘波体设计方法如图1(a)所示,A点为ICC 上的一点,AA'为ICC 上过A点的垂面,定义为密切平面,A'为曲率中心,D点为FCT 上的一点,它由AA'与FCT 相交得到,C点为密切锥壁面上的一点,B点为流线追踪得到的乘波体下表面对应点.在密切平面内,流线追踪方法与锥导乘波体设计方法完全一致,以图1(b)所示的密切平面AA'为例,O为锥形流的圆锥顶点,OC为锥面,OA为激波,D'为D点在激波上的投影点,D'B为流线.组合所有密切面的流线所得到的流面即可作为下表面乘波面,上表面一般是自由流追踪得到的流场.

图1 密切锥设计方法示意图Fig.1 Illustrations of osculating-cone method

传统的密切锥方法中,基准流场是锥形流,并且每个密切面内锥形流均相同.无黏锥形流作为拟二维流场,一般可通过求解Taylor-Maccoll 方程(下简称“T-M 方程”)快速生成.T-M 方程是一个常微分方程,形式如下

其中,Vθ和Vr为流场中任意一点处的速度分量,Vmax是总焓对应的最大速度,θ为射线与对称轴夹角.T-M 方程只有一个因变量Vr,Vθ可以根据锥形流的无旋条件求得:Vθ=dVr/dθ.

T-M 方程是一阶常微分方程,可以采用龙格库塔方法推进求解.当求解T-M 方程生成锥形流时,流场仅与马赫数和半锥角有关,并且马赫数和半锥角决定激波角.因此在不同的密切面内设定不同的马赫数或半锥角(激波角),可以得到使用不同锥形流场的密切锥设计方法,扩大设计空间.特别地,当不同密切面内基准流场的马赫数不同时,就是基于可变马赫数流场的密切锥方法.

1.2 定平面形状乘波体设计

定平面形状乘波体可以通过密切锥方法设计得到.在密切锥方法中,本文作者推导了设计曲线ICC,FCT 与所生成乘波体外形的平面形状轮廓线(planform contour line,PLF)之间的几何关系.选择标准坐标系,使用3 个函数c(x),f(y)和p(y)表示ICC,FCT和PLF,x,y为两个独立变量,c(x),f(y)和p(y)之间可用如下方程进行几何关联

其中,λ为当地后掠角,β为锥形流的激波角,具体推导请参考文献[10].式(2)是一阶非齐次常微分方程组,根据这个方程组即可实现给定平面形状的乘波体设计,而且进一步还可实现给定三维前缘线的乘波体设计.

式(2)的推导基于两个前提: (1)密切面内的流场激波为直线型;(2)不同密切面内基准流场的激波角相同.参考1.1 节中可变马赫数流场乘波体的设计思路,在不同密切面内使用马赫数不同锥形流场,并在求解T-M 方程时从相同的激波角出发生成流场,保证各密切面内的流场激波角相同,这样即可实现基于可变马赫数流场的定平面形状乘波体设计.

1.3 带上/下反翼的双后掠乘波体

选择文献[17]中的上反翼双后掠乘波体作为基准外形,如图2(a)所示,长8 m,翼展9 m,第1 后掠角75°,第2 后掠角50°,翼梢抬高0.8 m 生成上反翼.提取这个外形的三维前缘线设计乘波体,具体操作是: 首先将提取的三维前缘线沿俯视图和正视图方向,分别投影得到p和f;然后将p和f代入式(2)并使用数值方法求解得到c;最后将c和f作为设计曲线使用密切方法生成乘波体.此时外形的前缘线正是所提取的上反翼双后掠形状.

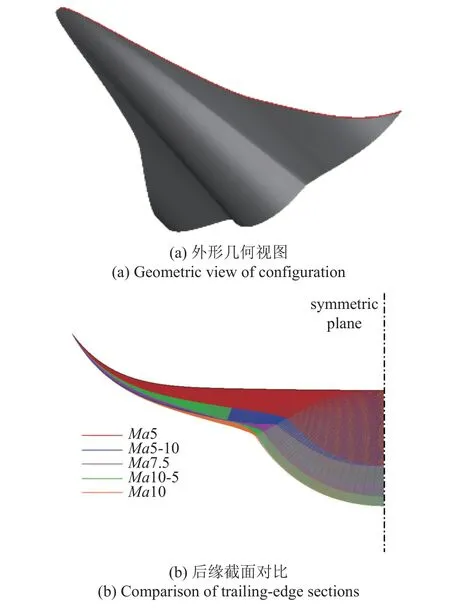
图2 基于不同马赫数分布流场的上反翼双后掠乘波体Fig.2 Double swept waveriders with wing dihedral based on different Mach number distributions

在不同密切面内布置不同马赫数的锥形流,设计高度30 km,激波角均设定为β=15°,简单起见,参考论文[18]的思路,设定中央对称面处的内侧马赫数Main和最外侧密切面的马赫数Maout,中间密切面的马赫数由这两端的值线性变化得到

其中i代表每个密切面,n为乘波体设计中密切面的数目.

表1 给出了本文测试外形的设计参数,其中Ma5,Ma7.5 和Ma10 外形为固定马赫数乘波体,基准流场分别在Ma=5,7.5,10 设计.Ma5-10 和Ma10-5 外形为可变马赫数乘波体,Ma5-10 外形的内侧马赫数为5、外侧为10,Ma10-5 外形的内侧马赫数为10、外侧为5.

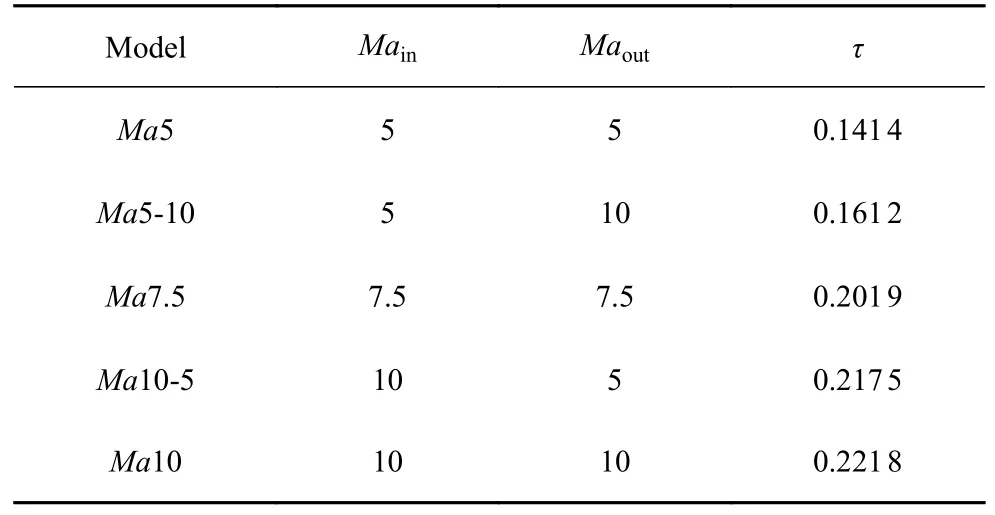
表1 可变马赫数外形的设计参数Table 1 Design parameters of waveriders from variable-Machnumber flows

外形的容积与设计马赫数有关,当激波角确定时,锥形流的马赫数越大,流线越远离物面,导致所生成的乘波体容积越大.表1 第4 列给出了不同外形的容积率τ=V2/3/S,其中V是容积,S是平面投影面积.容积率从小到大分别为Ma5,Ma5-10,Ma7.5,Ma10-5 和Ma10,这5 个外形平面形状相同,因此上述排序也是容积的排序.图2(b)展示了5 个模型的后缘剖面,Ma5-10 外形内侧厚度较小,外侧厚度较大,而Ma10-5 外形内侧厚度较大,外侧厚度较小,但因为内侧是主要的容积提供位置,所以Ma10-5 的容积大于Ma5-10 外形.

1.4 数值方法及网格收敛性

使用数值模拟手段评估外形的气动性能.数值方法采用有限体积方法求解三维可压缩Navier-Stokes 方程.无黏通量采用Roe 格式[19]计算,有权重格林-高斯公式重构方法获得空间二阶精度,梯度限制器选取改进的Barth 限制器[20],以消除计算中间断附近的数值过冲和振荡,同时应用基于压力辅助限制器的局部熵修正方法避免非物理解[21].黏性通量采用二阶中心格式计算.湍流模型采用在工程上广泛应用的Menter SSTk-ω两方程模型[22].时间方向采用二阶精度双时间步方法,LU-SGS 隐式推进求解[23].计算平台为我院自主研发的计算流体力学(computational fluid dynamics,CFD)数值模拟软件平台-GiAT,已经过大量理论和工程验证[24-27].

图3 给出了数值计算所采用的网络示意,为了保证激波与黏性流动的精确模拟,采用分区结构化网格.在激波间断位置网格尽量顺激波方向布置;黏性层法向网格尽量保证垂直壁面,流向参数梯度较大位置保证足够的流向网格密度.

图3 计算网格Fig.3 Computational mesh

以Ma5.5 外形为例分析网格收敛性.分别生成3 套不同尺度的网格: 稀疏网格Coarse,网格数494 万左右;中等网格Medium,网格数968 万左右;密网格Refined,网格数1914 万左右.

在状态H=30 km,Ma=7.5 评估气动性能,首先考察升阻力数据.表2 给出在攻角α=12°时升阻特性计算结果,可以看到medium 网格与refined 网格之间差异较小,均在0.9%以内,而coarse 网格则与密网格差异较大,最大差异为阻力系数3.94%.

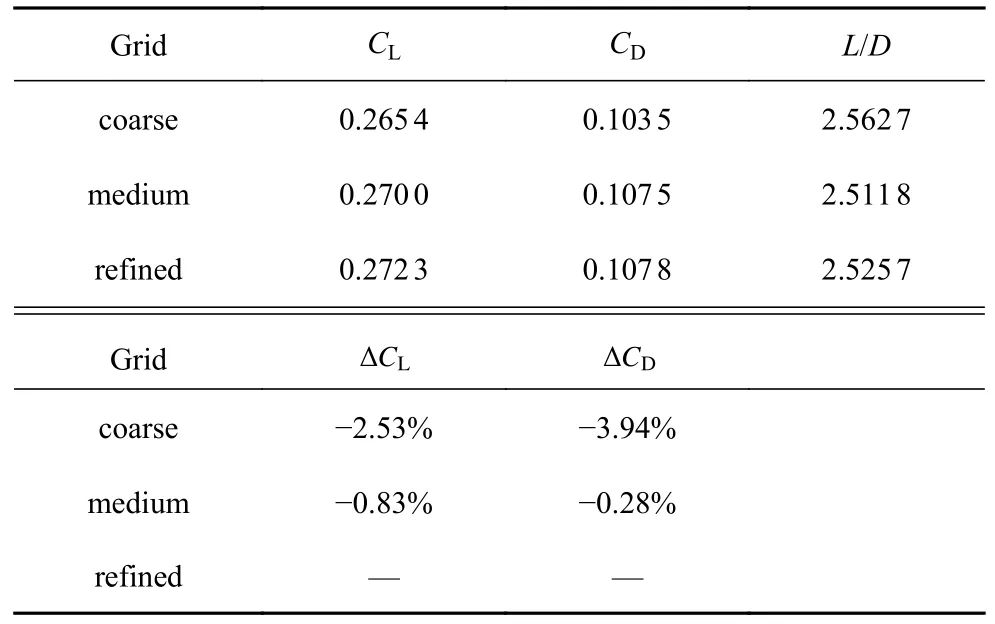
表2 不同网格的升阻特性结果Table 2 Lift and drag results of different grid

表3 给出轴向力系数、法向力系数和相对头部顶点的俯仰力矩系数结果,同样可以看到medium网格与refined 网格之间差异较小,均在0.8%以内,coarse 网格与refined 网格最大差异为轴向力系数的5.57%.

表3 不同网格的力矩结果Table 3 Moments results of different grid

考虑到medium 网格相比refined 在气动力、力矩方面的误差较小,而coarse 网格误差较大,本文认为medium 网格,即网格量968 万左右,是可信和足够的.

2 气动性能比较分析

2.1 升阻力对比

本节研究基于可变马赫数流场的定平面形状乘波体的升阻特性,并与相同流场的外形作对比.计算图2 中5 个外形的气动性能,计算状态为H=30 km,Ma=5,7.5,10.这5 个外形具有相同的平面投影形状和三维前缘型线,参考面积29.598 m2,参考长度8 m.

图4 给出零度攻角时5 个外形的升阻力随马赫数的变化.可以看到,Ma5-10 外形介于Ma5 和Ma7.5 流场设计的乘波体之间,Ma10-5 介于Ma7.5 和Ma10 乘波体之间,表明可变马赫数乘波体具有较均衡的综合性能.

图4 升阻力随马赫数的变化 (α=0°)Fig.4 Lift-drag characteristics variation via Mach number at α=0°

图4 升阻力随马赫数的变化 (α=0°) (续)Fig.4 Lift-drag characteristics variation via Mach number at α=0°(continued)

同时,外形的性能与容积密切相关,5 个外形的升力系数、阻力系数和升阻比由大到小的排序与容积率排序相反,而且Ma5,Ma5-10,Ma7.5 外形的容积率相差较大,而Ma7.5,Ma10-5,Ma10 外形的容积率差较小,这个容积差别的幅度也对应在气动力的差别上.

乘波体的最大升阻比一般不在零度攻角,对这5 个外形来说,最大升阻比一般在2°攻角取得.图5给出了α=2°时的升阻比,规律与在零度攻角是相同的.另外综合考虑图4 和图5 中升阻比的变化,可以看到同一攻角下,随着马赫数的增大,考虑底阻的升阻比数值有小幅度增加,而不考虑底阻的升阻比则有小幅度下降.

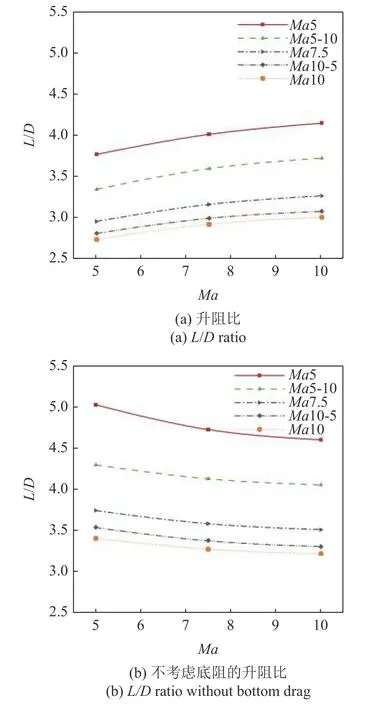
图5 升阻力随马赫数的变化 (α=2°)Fig.5 Lift-drag characteristics variation via Mach number at α=2°

2.2 纵向稳定性

本节分析可变马赫数乘波体的纵向稳定性.纵向稳定性可由气动焦点(aerodynamic center,A.C)和质心的相对位置确定,设定质心在全长的2/3 处,图6给出了可变马赫数乘波体Ma5-10 和Ma10-5 外形在Ma=5,7.5,10 时气动焦点随攻角的变化,并与Ma5,Ma7.5 和Ma10 外形作比较.这5 个外形均为纵向静稳定,且气动焦点位置非常接近,均在全长的67%～70%之间,表明基准流场对纵向稳定性影响很小.同时,当马赫数变化时,气动焦点的变化也很小,说明在高超声速阶段,当飞行状态偏离设计点时,纵向稳定性不会发生大幅改变.

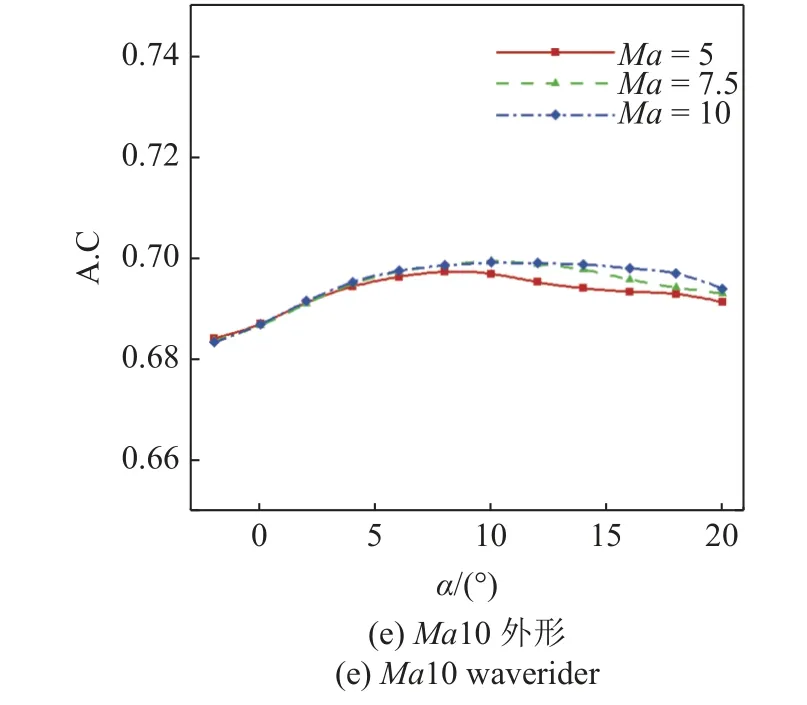
图6 气动焦点随攻角的变化Fig.6 Aerodynamic centers variation via angle of attack

一般来说,纵向稳定性与平面形状关系密切,从图6 所示的可变马赫数乘波体的焦点位置可以看出这一规律,即当乘波体的平面形状给定时,其纵向稳定性就基本确定了,不同马赫数的基准流场及其导致的乘波曲面变化对纵向稳定性的影响很小.

3 与相同平面形状的等容积外形比较

3.1 等容积的定平面形状乘波体

在3.2 节气动力的分析中可以看到,综合可变马赫数流场乘波体与固定马赫数流场乘波体的性能,发现升阻比与容积密切相关,考虑容积后可变马赫数流场外形并未表现出优势.之前学者们在比较可变马赫数流场乘波体与固定马赫数外形时,大都未考虑容积这一因素,同时很多工作中比较外形的平面形状也不同,导致所阐述的可变马赫数乘波体的性能优势值得商榷.

比如,在文献[3]中,使用内侧Ma8 流场和外侧Ma4 流场生成乘波体,与Ma4 和Ma8 外形作比较,这3 个外形的容积率均不同,平面形状也不同;在文献[18,28]中,分别设计了Ma10-6,Ma6-10 两个可变马赫数乘波体,并与Ma10 外形和Ma6 外形作对比,这4 个外形的平面形状相同,但容积均不同.在文献[15]中,设计了Ma10-4 外形,并与等容积率的Ma11.08 外形作比较.然而,虽然两外形的容积率相同,但平面形状和平面面积却不同.在文献[16]中,设计了Ma6-13 乘波体,并与Ma13 和Ma6 两个外形作对比,Ma6-13 外形的性能介于Ma6 和Ma13外形之间,这3 个外形的平面形状相同,但容积不同.在文献[29]中,设计了Ma6-12 和Ma12-6 两个可变马赫数流场外形,并与Ma6,Ma9 和Ma12 这3 个固定马赫数外形作比较,这几个外形容积不同,平面形状也不同.

容积和平面形状对乘波体的气动性能影响很大,在研究中有必要将这两个变量固定.因此本节提取图2(a)外形的前缘型线,保持激波角为15°不变,通过调整基准流场马赫数,生成了与可变马赫数乘波体容积相同的固定马赫数乘波体.图7 给出了固定马赫数外形的容积率随设计马赫数的变化,基本呈单调增长,增长率随马赫数的增加而降低.从图7中的数据计算得出,与Ma5-10 外形容积(τ=0.161 2)相同的固定马赫数乘波体外形为Ma5.50 外形,基准流场在Ma=5.50 生成;与Ma10-5 外形容积(τ=0.217 5)相同的为Ma9.25 外形,基准流场在Ma=9.25 生成.

图7 容积率随马赫数的变化Fig.7 Variety of volume efficiency via Mach number

图8 展示了可变马赫数乘波体与等容积固定马赫数乘波体在后缘截面的对比.

图8 与等容积乘波体的对比Fig.8 Comparison with equal-volume waveriders

3.2 气动性能比较

表4 给出了容积相等的可变马赫数和固定马赫数乘波体在α=0°时升阻比的比较,“ Δ ”表示同一状态下可变马赫数乘波体的升阻比相对于固定马赫数乘波体的相对偏差,负号代表可变马赫数乘波体的升阻比较小.可以看到,在容积相等、平面形状相同的条件下,当飞行Ma是5,7.5 和10 时,固定马赫数乘波体与可变马赫数乘波体的升阻比偏差都非常小,考虑底阻时的幅度均在1%以内,而且可变马赫数乘波体的升阻比小于固定马赫数外形.去掉底阻后,Ma5-10 的升阻比相比Ma5.50 外形变得更差,误差增大到1%以上;而Ma10-5 和Ma9.25 外形之间的误差均小于0.6%,升阻比性能非常接近.

表4 等容积乘波体的升阻比比较 (α=0°)Table 4 Comparisons of L/D with equal-volume waveriders(α=0°)

表5 给出了α=2°时升阻比的比较,Ma5-10 外形的升阻比变得比Ma5.50 外形更差;Ma10-5 虽然比Ma9.25 外形的升阻比略高,但偏差幅度最大只有1.29%,优势不明显.

表5 与等容积乘波体的升阻比比较 (α=2°)Table 5 Comparisons of L/D with equal-volume waveriders(α=2°)

因此,在高超声速阶段的宽速域范围内,当容积相同、平面形状相同时,可变马赫数乘波体的升阻比与固定马赫数乘波体相比没有优势,甚至还更低,类似结果在文献[30]中也有体现.结合2.2 节对可变马赫数乘波体纵向稳定性的分析,认为对乘波体宽速域升阻特性及纵向稳定性的改进应该着重于平面形状的设计优化,使用不同马赫数分布的流场改进乘波曲面,对于提升乘波体的升阻比及纵向稳定性优势不大.

在纵向稳定性方面,分别比较Ma5-10 外形和Ma5.50 外形以及Ma10-5 外形和Ma9.25 外形气动焦点的位置.表6 给出了Ma5-10 外形在3 个马赫数不同攻角时气动焦点位置相对于Ma5.50 外形的偏差,最大相对偏差只有1.6015%,差距非常小.表7为Ma10-5 外形的气动焦点位置相对于Ma9.25 外形的偏差,最大偏差绝对值更是只有0.78%.这些结果说明在容积相同、平面形状相同的情况下,纵向稳定特性基本一致.另外结合图6 的结果,可以进一步确认平面形状对纵向稳定性有决定性影响,而使用可变马赫数基准流场对乘波体的纵向稳定性基本没有影响.

表6 Ma5-10 与Ma5.50 外形气动焦点位置的相对偏差Table 6 Relative differences of A.C location between Ma5-10 and Ma5.50 configurations

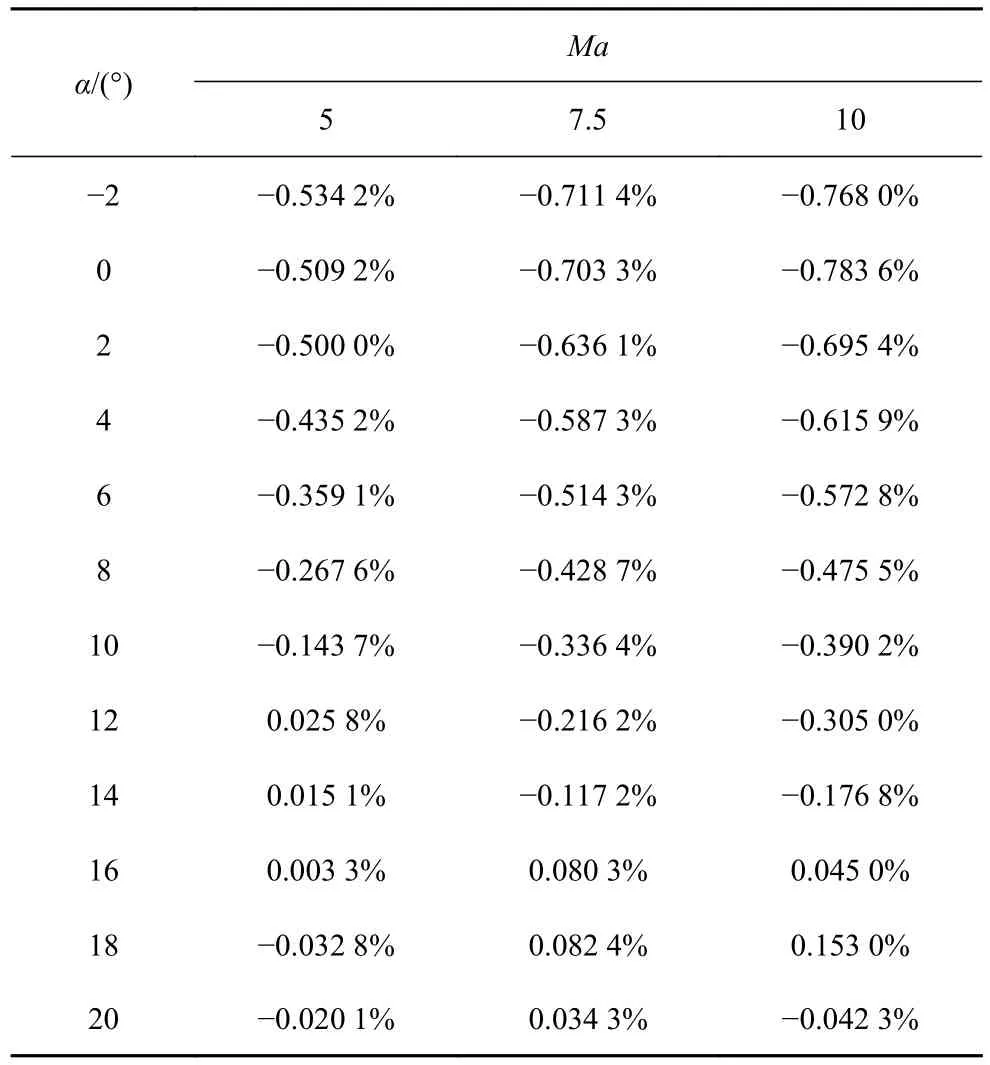
表7 Ma10-5 与Ma9.25 外形气动焦点位置的相对偏差Table 7 Relative differences of A.C location between Ma10-5 and Ma9.25 configurations

3.3 流场初步分析

图9 给出了Ma5.5 乘波体和Ma5-10 乘波体后缘压力分布在不同马赫数下的对比,可以看到,对于Ma5.5 乘波体,当计算马赫数高于5.5 时,激波向下表面靠近明显.另外,与Ma5.5 乘波体相比,Ma5-10乘波体下表面在对称面处更薄,激波位置与Ma5.5乘波体存在一定差异.同时,Ma5-10 乘波体沿展向第2 后掠区厚度大于Ma5.5 乘波体,所对应的下表面过激波后压力更高,这是由于沿展向设计的马赫数大于5.5,在高马赫数下压缩性更强.图10 给出的Ma9.25 和Ma10-5 乘波体后缘压力分布也体现了相似的规律,即对于设计马赫数更高的第2 后掠区压缩性更强.

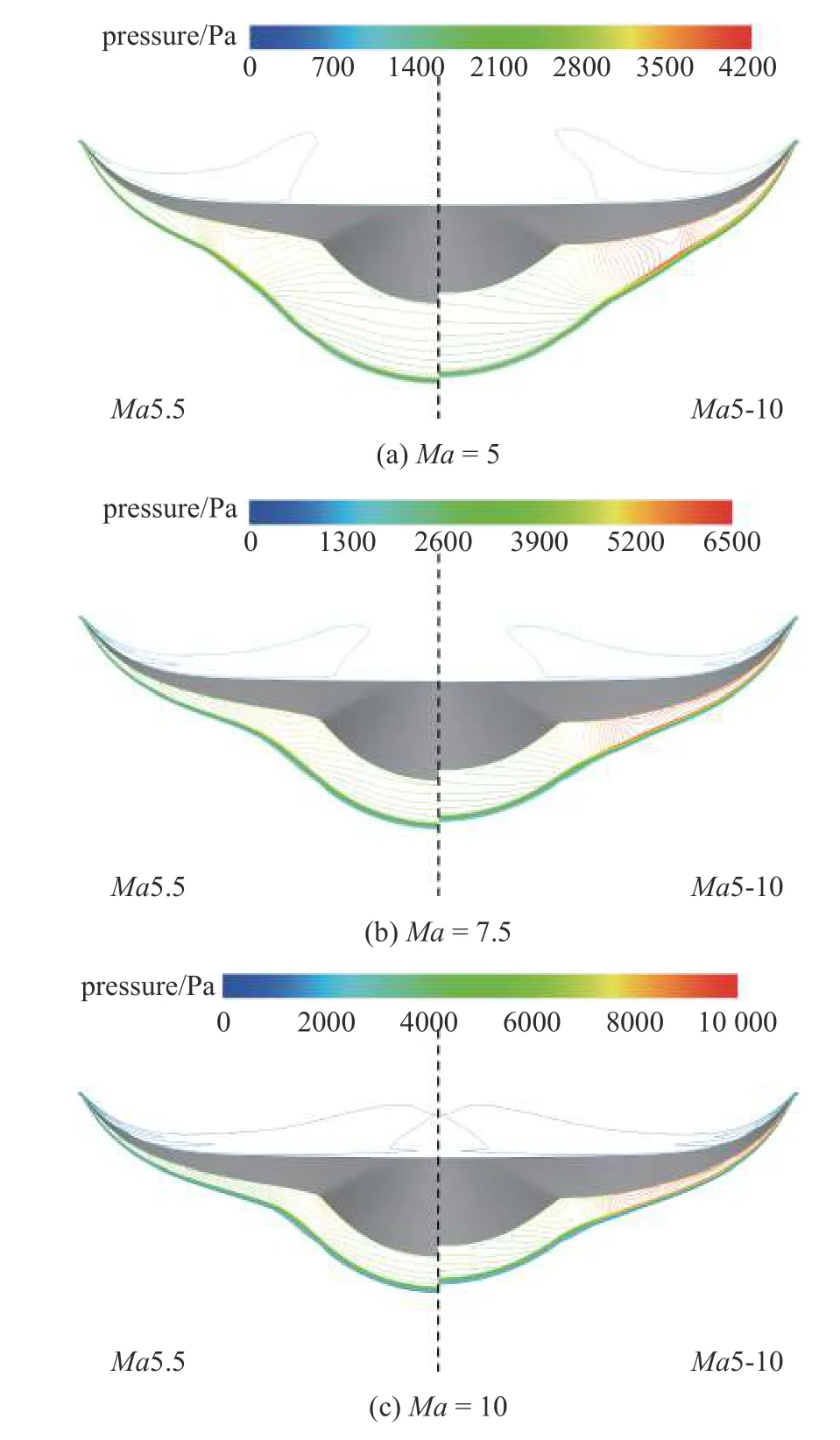
图9 Ma5.5 与Ma5-10 乘波体后缘压力分布(α=0°)Fig.9 Pressure distributions in trailing-edge sections of Ma5.5 and Ma5-10 waveriders (α=0°)

图10 Ma9.25 与Ma10-5 乘波体后缘压力分布(α=0°)Fig.10 Pressure distributions in trailing-edge sections of Ma9.25 and Ma10-5 waveriders (α=0°)

对于密切锥方法设计得到的乘波体,当计算马赫数低于设计马赫数时,下表面激波将会出现脱体的情况,导致前缘两侧出现溢流.如图9(a)所示,在Ma=5 的状态下,Ma5-10 乘波体外侧前缘处激波脱体较Ma5 乘波体更加明显.同样地,图10(a)所示,Ma9.25 乘波体外侧前缘处激波脱体较Ma10-5 乘波体更加明显.而由图9(c)和图10(c)可以看到,当来流马赫数高于设计马赫数时,无论是对于固定马赫数乘波体还是可变马赫数乘波体下表面激波均能较好地附着于前缘,保持了较好的“乘波”特性.

在特定马赫数下,可变马赫数乘波体的部分区域确实会保持明显的“乘波”特性,但其他区域却不可避免地会背离“乘波”特性,对于宽速域气动性能的提升并不明显,反而部分可变马赫数乘波体反而会导致气动性能略微下降,综合来看反而不如使用固定马赫数流场设计的等容积外形.