理想后视镜绕流影响下边界层壁面压力脉动研究1)

刘伯峰 吴 霆 朱力行 ,2)

* (中国科学技术大学近代力学系,合肥 230026)

† (中国科学院力学研究所非线性力学国家重点实验室,北京 100190)

** (中国科学院大学工程科学学院,北京 100049)

引言

流致振动和噪声现象广泛出现在各类工程应用领域[1].飞行器、车辆和水下潜航器在壁面附近的湍流流动往往是气动和振动噪声的主要来源[2].湍流流动引起的壁面压力脉动会激励板壳结构振动并进一步向内辐射引起内部噪声.民用飞行器中,机舱内的噪声水平与乘客感受密切相关: 低频噪声直接引起乘客不适;而接近人类语音频率范围的中频噪音会干扰口头交流[3].水下潜航器中,声呐罩受激振动产生内部噪声并传入水声换能器,降低了声呐的信噪比,减小了潜航器航行时声呐的探测范围[4].乘用车的内部噪声和振动水平是影响车辆乘员舒适度的关键因素.因此,汽车工业设计了一套包含噪声、振动和平顺性(NVH)等要求的综合设计指标,并围绕NVH 开展设计和优化工作.综上所述,流致振动与噪声的预测具有重要的工程价值.

气动/振动声学响应主要包括结构振动和内外部噪声的空间分布和频率谱.需要针对流致振动和噪声向外和向内的辐射和传播过程开展相应的气动-振动声学分析.气动/振动声学分析的主要方法包括解析法、统计方法和数值方法.解析法主要基于模态分析,适用于具有规则形状和简单几何的对象,如带肋的曲面平板[5].统计能量分析法首先确定系统内不同组件构成的子系统之间能量分布的情况,然后基于代理模型计算平均振动声学响应[6].计算气动-振动声学分析中,可以通过各类经典的离散方法(有限元或边界元)来表示实际工程问题中难以解析表达的复杂几何和非均匀材料系数,并通过求解线性系统得到振动声学响应[7-8].

流致振动和噪声的气动/振动声学分析的一个主要问题是确定激励源(流动发声声源).激励源中各项声源函数,可分为单级子、偶极子和四极子或更高阶源项[1].由于声源辐射功率与马赫数的高次幂相关,低马赫数流动中的噪声声源主要为偶极子,也即壁面压力脉动.现代喷气式客机的引擎噪声水平较低,巡航阶段舱内噪声主要来自客机机身圆柱壳体表面充分发展的湍流边界层[9].同时,水下潜航器的平直中段也可以被模化为湍流边界层激励下的水平或曲面板[10].因此,本文主要关注充分发展的湍流边界层的壁面压力能谱模型.

考虑到平板边界层压力脉动的随机特性,壁面压力模型往往呈现为时空关联或波数-频率能谱.剪切湍流中的壁面压力时空性质的详细讨论参见Wu等[11]的综述文章.基于壁面压力脉动的时空性质,文献中报告了一系列零压梯度湍流平板边界层壁面压力脉动模型.经典经验模型的详细论述和比较可参见Miller 等[12]的评述文章.这些半经验模型被广泛用于前述各类工程应用中的振动声学分析: Corcos模型[13]是壁面压力脉动时空关联模型早期研究中的代表性工作;Efimtsov 模型在空间关联中考虑了边界层厚度和马赫数的影响,并被用于航空工程中结构振动和内部噪声的预测[14];Chase 模型被用于开展对理想水下潜航器外壳的振动声学分析[5];Smol'yakov 模型被用于插值以提高振动声学实验数据的解析度[15].

在工程应用中,来流通常为充分发展的湍流边界层,并受到钝体阻挡后形成复杂流动[16-17],比如水下潜航器的围壳[18]和汽车后视镜绕流[19-22].这类问题中,受钝体尾迹影响的复杂湍流流动往往成为气动/振动的主要声源.由于钝体尾迹的影响,该类流动的壁面压力脉动无法采用仅考虑不同压力梯度下的平板边界层等简单情况的压力脉动模型.对这一类流动,亟需开展壁面压力时空特性的相关研究,分析钝体尾迹影响下壁面压力时空特性相对于平板边界层的变化,为适用于该类复杂流动的壁面压力模型提供模化依据,从而减小气动/振动噪声的预测成本并提高预测精度.本工作采用大涡模拟方法,得到了钝体尾迹影响下边界层壁面压力脉动,并开展了相关理论分析,以期为复杂流动下的壁面压力能谱模化提供参考.

1 问题介绍: 车辆后视镜绕流

随着新能源汽车的发展,汽车发动机等声源引起的噪声已经得到了明显的改善,风噪问题成为制约汽车NVH 的主要问题之一[23].Buchheim 通过风洞实验测量了汽车时速在典型高速公路工况(来流速度为110 km/h)下引起的内部噪声可达78 dB[24],严重影响乘员驾乘感受.汽车风噪的主要来源为后视镜绕流引起的车窗表面的压力脉动.为了更好地研究流致声源,业界提出了理想化的汽车后视镜模型作为标模[25].围绕该标模,研究者开展了一系列数值模拟[19-22]和实验研究[26].本工作主要关注钝体尾迹影响下的边界层壁面压力脉动的时空性质.理想汽车后视镜绕流为典型的钝体绕流,在文献中有较为丰富的实验测量和数值模拟的参考结果,可以较为方便地验证数值结果以支撑理论分析.

后视镜绕流的几何配置包含理想汽车后视镜与平板,如图1 所示.理想汽车后视镜由半圆柱和1/4 球组成.其中,1/4 球的半径和半圆柱底面半径均为Dmr=0.1 m,半圆柱的高为 2Dmr=0.2 m.平板由两部分组成: 半径为0.8 m 的半圆形前缘和边长为1.6 m 的正方形后缘.设置正方形后缘的目的在于模拟车辆后视镜之后的玻璃车窗以及金属门框.玻璃车窗选定为平板正方形后缘中心处长方形区域,其流向长度为1.4 m,而展向宽度为1.2 m.该长方形玻璃窗区域紧贴后视镜,是流致振动和噪声的主要激励源的发生点.本文也将从该区域提取壁面压力脉动的空间分布和时间历史.后视镜与平板的相对位置如图1 所示.除了前缘形状,整体设置与经典理想后视镜绕流的实验设置[25]完全一致.实验中通常采用方形前缘,而数值模拟中方形[22]和半圆形前缘[20]在文献中均有出现.设置前缘的目的为使得来流在平板上发展为湍流,数值模拟中的半圆形前缘选型主要出于节省计算域的考量.

图1 后视镜绕流几何配置: 理想汽车后视镜与平板 (单位: m)Fig.1 Schematic diagram of the problem: a generic side mirror and a plate (unit: m)

2 数值方法与计算设置

2.1 控制方程与湍流亚格子模型

汽车在高速公路上的时速介于100～120 km/h,相应马赫数约为0.1.该工况下,后视镜绕流的可压缩效应并不显著,但是相关文献表明壁面压力脉动中的声模态不可忽略[21].因此,我们选用滤波后的可压缩Navier-Stokes 方程作为理想后视镜绕流的控制方程如下

其中 ρ,u,p,e0和T分别为密度、速度矢量、压力、内能和温度.σ=-2µ(∇·u)I/3+µ(∇u+∇Tu) 为黏性应力张量.式(1)、式(2)和式(3)分别为质量、动量和能量守恒方程.为了进一步封闭上述3 个偏微分方程,需要引入热力学状态方程.考虑到汽车在高速公路的工况下,流动介质为空气,马赫数较小,温度变化有限,因此采用理想气体状态方程.

在可压缩流动大涡模拟中,我们引入Favre 滤波以避免在连续方程中引入亚格子项.Favre 滤波定义为.动量守恒方程(式(2))中的非线性对流项在滤波后会出现亚格子应力张量 τ,采用涡黏模型模化该亚格子应力项如下

其中 µt为亚格子涡黏,kSGS为亚格子湍动能.本工作的大涡模拟采用两种不同的涡黏亚格子模型:Smagorinsky 模型[27](以下简称SMA 模型)和Wall adaptive local eddy-viscosity 模型[28](以下简称WALE 模型).能量守恒方程(式(3))中非线性对流项滤波后出现的亚格子热通量基于雷诺比拟模化.换言之,我们采用湍流普朗特数Prt=0.7 和亚格子涡黏系数模化亚格子热扩散系数.

2.1.1 Smagorinsky 模型

Zang 等[27]将不可压缩流动大涡模拟中的经典Smagorinksy 模型延伸到了可压缩流动.亚格子涡黏系数和亚格子湍动能均通过Favre 滤波后的对称剪切率=(+)/2 构造如下

其中,Δ 为滤波宽度,实际计算中,选取当前单元体积的立方根作为滤波宽度.式(5)和式(6)中的系数取值按Zang 等[27]的建议设为CR=0.012 和CI=0.006 6.由于Smagorinsky 模型主要适用于充分发展的各向同性湍流,采用Van Driest 修正[29]以减少壁面附近的亚格子涡黏.

2.1.2 WALE 模型

WALE 模型基于可解尺度的对称应变率张量和旋转张量的相关不变量构造,考虑了旋转的影响.另一方面,WALE 模型给出的涡黏系数近壁面以O(y2)的趋势衰减,不用施加额外的壁面修正[28].基于WALE 模型的涡黏系数表达式为

2.2 计算设置

为了适配理想后视镜和平板的几何形状,汽车后视镜绕流大涡模拟的计算域由1/4 圆球和半圆柱组成,如图2 所示.其中,1/4 球的球心与理想后视镜底面圆心重合,其半径为2.1 m;而半圆柱底面与1/4 球在法向贴合,半圆柱在流向长度为6 m.图2显示,入口来流离理想后视镜前缘的流向距离为2 m.该距离保证了空气在流过后视镜前能充分发展,并遏制反射波对入口的干扰.同时,后视镜后缘距离下游出口的流向距离为6 m,大约为60 倍的后视镜底面半径,可以保证后视镜绕流尾迹在达到出口前已经充分耗散.

图2 计算域设置 (单位: m)Fig.2 Computational set-ups (unit: m)

参考汽车在高速公路实际形式的工况,以及理想后视镜绕流的相关数值[19-22]和实验研究[25]中的流动设置,我们设置相应的来流和边界条件.来流速度为u∞=38.89 m/s,也即140 km/h.来流密度选用空气在常温大气压下的密度 ρ∞=1.198 kg/m3.远场参考压力为标准大气压p∞=1.013 25×105Pa.远场温度为常温T∞=293 K.来流的运动学黏性为ν=1.522 4×105m2/s.该计算设置中,基于后视镜底面直径的雷诺数为Re≈5.2×105.后视镜表面及其附属平板(见图2 中红色和蓝色区域)被施加了无滑移无穿透壁面条件,而计算域底面的其他位置仅被施加了无穿透边界条件.

本文中的大涡模拟采用分块结构网格对计算域进行网格划分,具体分块设置见图2.为了充分解析湍流边界层,网格在后视镜和平板表面加密.特别地,由于计划在玻璃窗口(图2 中蓝色区域)收集壁面压力脉动信息并开展谱分析,因此在流向和展向均额外加密了该区域.相似地,法向网格沿壁面作了拉伸,近壁面第一层网格离壁面的法向距离为 2.0×10-5m.网格中的节点总数约为 5.88×106.经后验检验,该网格解析度满足壁面解析大涡模拟的要求.空间插值采用二阶中心差分.时间推进采用二阶后向差分(BDF2),时间推进步长设置为 Δt=2.0×10-6s.本工作中大涡模拟均通过开源流体力学计算软件OpenFOAM 执行.我们选用了该软件中的rhoPimpleFoam 求解器(隐式时间压力基求解器)来求解低马赫数可压缩流动.

3 结果与讨论

3.1 计算验证

本工作主要关注壁面压力的时空性质,因此首先检验壁面压力的相关统计量以验证大涡模拟的结果是否可靠.本文工作开展的大涡模拟过程中,待来流两次流经全计算域,开始收集壁面压力的时间历史.通过对该时间段内的相关统计量的分析,此时流动充分发展并进入统计定常阶段.

3.1.1 时均压力系数

如图3 所示,在后视镜和玻璃窗表面特定位置收集了壁面压力脉动的时间历史.首先比较后视镜表面不同位置处的时均压力系数 〈Cp〉t,其定义如下

图3 后视镜绕流壁面压力脉动探测点: 后视镜表面(S1～S8)和玻璃窗表面(S9～S10)Fig.3 Arrangement of pressure sensors: the side-mirror surface(S1～S8) and the window surface (S9～S10)

其中,〈ϕ〉t(x) 表示对 ϕ (x,t) 开展时间平均,而下标(·)∞代表远场(来流)参数.待流动发展稳定后,在总时长为 0.409 6 s 的时间内,每隔10 个时间步收集了壁面压力,最终得到了长度为20 480 的时间序列.经过系综平均后,列出了7 个不同位置探测点处的时均压力系数.探测点坐标及相应 〈Cp〉t分别列于表1 和表2.表2 的最后两行比较了本工作中基于两种不同亚格子模型开展的可压缩大涡模拟的结果.两者在不同探测点得到的时均压力系数非常接近,S2和S3 两个探测点的误差不到5%,S4,S6 和S7 这3 个位置的误差不到2%,而S1 和S5 的误差也仅有10%左右.表2 也展示了文献中的实验结果[25],以及不同求解器配合不同亚格子模型得到的数值结果[19-21].本文得到的结果与文献中数值与实验结果总体均比较接近.因此,本工作中的大涡模拟准确预测了后视镜表面的时均压力系数.

表1 后视镜表面探测点坐标：S1～S10 (坐标原点为后视镜底面前缘,单位: m)Table 1 Coordinates of pressure sensors: S1～S10 (the origin ofcoordinate system rests in the front of the mirror's bottom,unit: m)

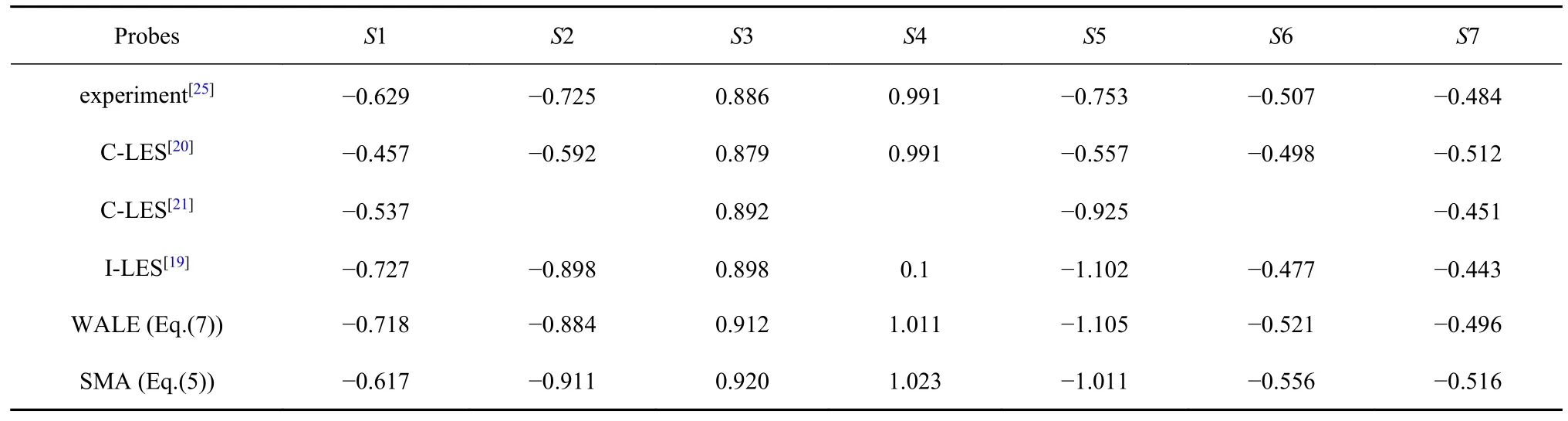
表2 后视镜表面探测点的时均压力系数：S1～S7Table 2 Time-averaged pressure coefficients at various locations on the side mirror: S1～S7

3.1.2 壁面压力脉动频率谱

验证了壁面压力的平均量后,进一步考察壁面压力脉动频率谱.对于特定位置的壁面压力时间历史p(x,t),首先得到平均压力 〈p〉t(x),然后得到脉动量p′(x,t)=p(x,t)-〈p〉t(x).然后,我们将时间域的壁面压力脉动通过离散傅里叶变换至频率谱,也即

其中,fl=l/(NtΔtS) 为离散频率序列,而tj=jΔtS为离散时间序列.Nt为时间历史的样本数,而ΔtS=10Δt为采样时间间隔.l∈[-Nt/2,Nt/2-1] 和j∈[0,Nt-1]均为整数.我们将采样时间分为9 个前后重合50%的节段,每个节段的时间序列长度为4096.得到每个节段的单边功率谱密度之后,在样本间开展系综平均如下

其中,Nseg=9 为时间序列节段数,而 ψpp为系综平均的单边功率谱密度.

对探测点S8,S9 和S10 (位置见图3)处得到壁面压力时间历史按上述方法得到单边功率谱密度.图4 展示了本文基于不同亚格子模型得到的大涡模拟结果,以及实验[25]和不同设置下的数值结果[20-21].图4 中,基于不可压缩分离涡模拟得到的S8 和S9两个位置处的壁面压力功率谱密度与其他结果均有较大偏差,说明DES 方法并不能准确地预测后视镜绕流的主要声源-壁面压力脉动.LES 结果,包括本文基于WALE 和SMA 模型的大涡模拟以及文献中报告的结果,在低频部分与实验测得结果比较接近,但在高频部分(1000 Hz 以上)会显著低于实验值.Zhu 等[30]在槽道湍流的壁面压力脉动频率谱中也报告了类似现象.该工作中,滤波直接数值模拟和大涡模拟得到的壁面压力频率谱在高频范围内远低于直接数值模拟结果.该现象主要原因在于大涡模拟中网格分辨率有限.由于壁面压力能谱的时空关联,空间截断也体现在了时间上,具体表现为频率谱在高频部分的能量明显偏低.探测点S8 中,WALE 模型的频率谱在500 Hz 以上较实验值偏高.探测点S9 中,SMA 模型的频率谱在1000 Hz 以上与实验值偏差较大.探测点S10 中,两个亚格子模型的频率谱在1000 Hz 以上均远低于实验值.综合S8,S9 和S10 这3 个探测点的功率谱密度,可以认为本文中的两种亚格子模型的大涡模拟结果在500 Hz 以下均与实验值相符.因此,之后的谱分析中,将主要关注500 Hz 以下的结果.

图4 无量纲壁面压力脉动单边功率谱密度 ψpp/(0.25Dmr).实线为本文大涡模拟结果(WALE 和SMA),红色圆圈是实验结果[25],三角和方块为文献中的数值结果[19-20]Fig.4 Dimensionless PSD of wall pressure fluctuation ψpp/(0.25Dmr).Solid line (WALE and SMA in present work),red circles (experimental reference[25]),and triangles and squares (numerical reference[19-20])

3.2 流场特性

为了定性讨论后视镜绕流特性,在图5 中展示了基于时间平均速度场的流线.速度场提取自基于SMA 亚格子模型的大涡模拟结果.按流经后视镜的不同位置,用不同颜色标注了不同的流线.红色为流经后视镜顶部的流线,而蓝色为流经后视镜侧面的流线.图5(a)中可以观察到,红色流线和蓝色流线分别勾勒出了两个不同回流区,分别称之为中部回流和侧向回流.图5(b)提供了侧面视角,图中观察到顶部剪切层由流经后视镜分离后于后视镜下游再附,形成了中部回流区.结合图5(b)和图5(c)两个视角,流经后视镜侧面的侧向剪切层形成了侧向回流区.观察图5(c)和图5(d)中后视镜平板上的流线,观察到流动被后视镜阻挡后形成了两个尾迹分支.

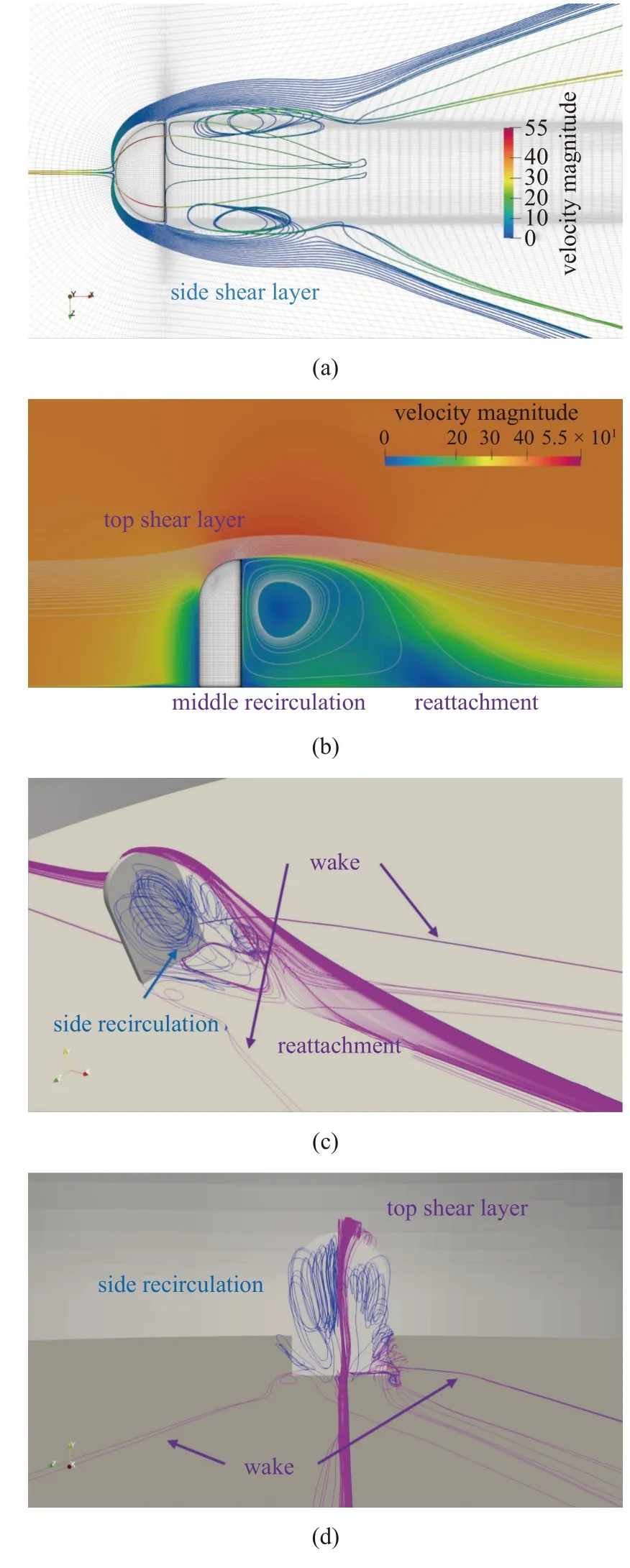
图5 大涡模拟时均流场流线(SMA 模型): 蓝色为流经后视镜侧面的流线,红色为流经后视镜顶部的流线Fig.5 Streamlines of time-averaged flow fields in LES (SMA): blue are those passing around lateral sides,and red are those going over the top

汽车工业已经充分认识到图5 中的后视镜绕流再附于玻璃窗会引起较大的壁面压力脉动,形成较强的气动/振动噪声[25].作者计算了图1 中玻璃窗(深灰色区域)上壁面压力脉动方均根.基于SMA 模型的大涡模拟数值结果,在图6(a)中绘制了该采样区域的壁面压力脉动方均根的空间分布.图中的壁面压力脉动方均根已通过远场密度和速度归一化(也即).图中可以观察到,后视镜下游出现了两个壁面压力较为集中的区域.对比图5 中时均流场,发现壁面压力脉动最大的区域并非顶部剪切层再附的位置,而是在侧向剪切层产生回流的位置.在图6(b)中,通过瞬时流场的Q等值面刻画了后视镜绕流产生的拟序结构.其中,流经后视镜侧方的剪切层引起的侧向回流附近能观察到更多涡脱落.该区域与观察到的强壁面压力方均根区域一致.图6(a)中的壁面压力脉动的分布在后视镜下游呈现以特定角度发生偏转.该偏转角度恰于图5(d)中观察到的尾迹分支一致.综上所述,来流流经后视镜后在下游玻璃窗上方形成了较为复杂的流动状态,引起的壁面压力脉动在流向和展向的空间分布不均匀,无法简单地通过湍流边界层模型来模化壁面压力作为气动/振动声学分析的声源.

图6 基于SMA 模型的大涡模拟结果Fig.6 LES results with SMA model

3.3 壁面压力谱分析

在分析了壁面压力脉动方均根的空间分布后,进一步通过谱分析研究后视镜绕流影响下的壁面压力脉动的时空性质.首先将壁面压力脉动p′(x,z,t)通过离散傅里叶变换从物理域变为波数-频率域,如下

其中,kn=2πn/Lx和kq=2πq/Lz分别为流向和展向的离散波数序列,而xm=mΔxS和zp=pΔzS分别为对应的离散坐标.Lx=1.4 m 和Lz=1.2 m 分别为玻璃窗在流向和展向的长度,Nx和Nz分别为流向和展向采样点个数,而 ΔxS和 ΔzS分别为流向和展向采样空间间隔.m∈[0,Nx-1],n∈[-Nx/2,Nx/2-1],p∈[0,Nz-1]和q∈[-Nz/2,Nz/2-1] 均为整数序列.得到波数-频率空间内的壁面压力脉动系数后,即可得到归一化的壁面压力脉动波数-频率能谱如下

波数-频率能谱处于三维空间中,为了方便讨论,计算偏转方向的能谱χc(kc,ω) 如下

其中,α 为偏转角,通过近壁法向平面(y=2.0×10-3m)中时均速度最小位置的速度矢量确定.

图7 中分别展示了基于两种亚格子模型得到的壁面压力脉动能谱.在波数频率坐标下,壁面压力脉动能谱存在3 种明显的能量集中区域(图7 中的山脊).通过考察这些集中区域的对流速度 ω/kc,这3 种集中区域对应的流动物理分别是: 声学峰,水动力对流峰和回流峰.声学峰体现湍流运动发声.考虑到声源通常以水动力对流速度被输运,因此声传播速度范围大约为u∞±c∞.其中c∞为介质中的声速.图7中,用红色虚线标记出声运动的特征速度.水动力对流峰体现流动输运作用,对应能谱峰值的能量显著高于其他特征运动对应的峰值.平板边界层中,壁面压力对流速度通常为 0.65u∞.图7 中,用紫色和绿色虚线分别标记 0.3u∞和u∞作为水动力对流速度的上限和下限.能谱中的回流峰体现第3.2 节中观察到的玻璃窗上方的回流区,该区域的特征速度为负,速度范围是 [-0.15,-0.675]u0,通过黑色和蓝色虚线在图7中标记.两种不同亚格子模型的大涡模拟结果之间相比,壁面压力能谱的定性性质一致,能谱中峰值位置的分布一致.然而,WALE 模型中的声学峰能量相比SMA 模型的结果稍强.

图7 玻璃窗口内无量纲壁面压力时空能谱(对流方向).虚线对应的特征速度分别为: 红色(± c∞+u∞)、绿色(u∞)、紫色(0.3u∞)、黑色(-0.15u∞)和蓝色(-0.675u∞)Fig.7 Wall pressure wavenumber-frequency spectrum χC.Phase speeds denoted by dashed lines are: red (± c∞+u∞),green (u∞),purple (0.3u∞),black (-0.15u∞),and blue (-0.675u∞)

为了进一步分析壁面压力能谱,在图8 中展示特定频率(也即 ω0/(2π)∈[100,200,500] Hz) 下的空间谱χ(kx,kz,ω0).从图中可以看出,在波数趋向于0 时(|k|→0),能谱出现一个山谷.该现象与Kraichnan-Phillips 定理[30]的表述一致.比较图8 中不同频率的空间谱,随着频率的提高(自左往右),能谱峰值沿着流向波数kx移动,体现了典型的水动力对流运动.特别地,也观察到后视镜绕流的壁面压力空间谱与湍流边界层存在区别.图7 中,空间谱等值线不再为椭圆,原本平行于展向波数的长轴发生了弯曲.该现象在图8 中500 Hz 对应的空间谱更为明显.文献[20]中的数值研究也报告了类似现象.空间谱等值线长轴的弯曲体现了流动经过后视镜以特定角度发生了偏转.此外,在流向波数kx为负的区域同样有一较弱的能谱峰值区域.这是由于流动在后视镜后方产生了回流,从而导致脉动压力有向上游传播的分量.

图8 不同频率下玻璃窗口内无量纲压力波数谱: 频率范围 ω0/(2π)∈[100,200,500] Hz (从左至右)Fig.8 Dimensionless wavenumber spectra of wall pressure on the window at various frequencies: ω0/(2π)∈[100,200,500] Hz (from left to right)

3.4 主传播方向的壁面压力脉动

本文在第3.2 节讨论了湍流边界层流经后视镜后,在后视镜下游玻璃窗区域内产生了较为复杂的湍流流动.在第3.3 中,通过谱分析研究了后视镜绕流产生的壁面压力脉动.分析结果显示,相比于平板湍流边界层,后视镜绕流下游玻璃窗存在多种流动引起的壁面压力脉动成分.因此,为了准确描述压力脉动在玻璃窗内各个位置的对流速度,采用泰勒冻结假设[11] 来描述脉动压力的特征传播速度C=(Cx,Cz).根据泰勒冻结假设,压力脉动和其传播速度应满足如下偏微分方程

泰勒冻结假定没有考虑湍流的随机横扫效应,因此上述方程仅在系综平均的情况才成立.因此,通过最小二乘法可以求出C

其中p′(x,z,t) 为大涡模拟中流动发展稳定后收集的壁面压力空间分布和时间历史.

压力脉动的对流速度C的流线如图9 所示.图中可以观察到,玻璃窗上的壁面压力脉动对流速度可以明显分为3 个区域: 回流区、稳定对流区和过渡区.玻璃窗紧贴后视镜的区域有封闭流线,为回流区.回流区下游,存在一个明显的对流速度方向平行、速度大小分布稳定的区域,也即稳定对流区.该区域压力脉动对流方向与来流速度形成一个稳定的夹角.该夹角本质上即为先前在节3.2 中提到的偏转角 α.SMA 模型和WALE 模型的结果中,流线与水平方向夹角分别为 α=11.60 和 α=13.31.回流区下游沿着流向中心线的压力脉动对流速度依然严格为流向,并且随着展向位置的变化,逐步过渡到稳定的偏转角.该区域为过渡区.此外,图9 中存在一个对流速度大于来流速度的区域(红色流线区域).这是由于(15)式中假定了壁面压力脉动的输运为流向-展向平面内的二维运动.实际上,该假定在复杂流动中(如本工作中的后视镜绕流)并不完全满足.出现对流速度过快的情况的区域很可能存在法向的压力脉动输运.

图9 玻璃窗口处的无量纲对流速度的流线分布和偏转角Fig.9 Streamlines and the deflection angle of the convection speed on the window

3.4.1 稳定对流区的壁面压力谱分析

通过提取壁面压力脉动的对流速度,在图9中确定了稳定对流区.对流速度在该区域内的分布恒定,没有明显的梯度变化.同时,对流速度与流向呈固定夹角,体现了图5 中的尾迹分支.在该区域内提取壁面压力脉动的波数-频率能谱以分析后视镜绕流中特定流动引起的壁面压力成分.谱分析的采样窗口为平行于坐标轴的正方形,顶点坐标为(x,z)=(0.8,0.0) m,正方形边长为 0.4 m.将该正方形逆时针旋转 α 角度,如图9 所示,以贴合对流方向.在进行谱分析之前,将该正方形区域内的壁面压力脉动投影到平行于偏转角的方向,也即 (x,z)→(x′,z′).坐标映射关系为:x′=xcosα-zsinα 和z′=xsinα+zcosα.最后,根据式(13),得到稳定对流区内的壁面压力脉动时空谱χs(,,f).由于旋转后的坐标轴x正方向与对流速度方向一致,因此偏转方向的能谱为χc(kc,f)=χs(,f).

将稳定对流区中偏转方向的壁面压力波数频率谱绘制于图10,包括不同亚格子模型得到的结果.图10 显示,与玻璃窗全场的压力能谱相比,能谱中不存在负对流速度的回流区,仅有对流峰和声学峰.该区域内的壁面压力脉动能谱中,对流峰大于声学峰的能量.比较图10(a)和图10(b)中的能谱,基于不同亚格子模型得到的大涡模拟结果定性上没有差别.稳定对流区的压力波数频率谱表明,该区域内仅有对流和声两种特征流动,与平板湍流边界层中的流动成分一致.因此,进一步提取了特定频率(也即ω0/(2π)∈[100,200,500] Hz)下的空间谱χ(kx,kz,ω0),见图11.稳定对流区在特定频率下的空间谱在零波数附近存在山谷区域,满足第3.3 中讨论的Kraichnan-Phillips 定理.另外,随着频率的增加,空间谱的峰值位置也沿着流向波数的正方向运动,体现了水动力学对流的特性.通过比较图11 与图8,发现稳定对流区的壁面压力空间谱等值线呈现相对标准的椭圆形,没有出现玻璃窗内压力空间谱的弯曲现象.这表明稳定对流区的壁面压力脉动的时空性质很可能与平板湍流边界层的相关特性一致.

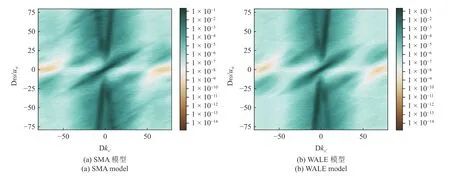
图10 稳定对流区内无量纲壁面压力脉动波数频率谱Fig.10 Dimensionless wall pressure wavenumber-frequency spectrum in the steady-convection zone

图11 不同频率下稳定对流区内无量纲化压力波数谱: 频率范围 ω0/(2π)∈[100,200,500] Hz (从左至右)Fig.11 Dimensionless wavenumber spectra of wall pressure in the steady-convection zone at various frequencies: ω0/(2π)∈[100,200,500] Hz (from left to right)

3.4.2 稳定对流区的壁面压力脉动空间关联

上一节中的壁面压力谱分析表明,稳定对流区的壁面压力很可能具备平板湍流边界层的时空特性.为了定量验证这一结论,在本节分析该区域内的壁面压力脉动的空间关联.首先将通过离散傅里叶变换得到的频率谱壁面压力系数(x,z,ω) 投影到旋转后的坐标系(x′,z′,ω) (见第3.4.1 节).然后,计算不同频率 ω 下,稳定对流区的壁面压力脉动的空间关联系数

在100 Hz 和200 Hz 下稳定对流区的壁面压力关联系数的空间分布见图12.基于两种不同亚格子模型的大涡模拟结果并无定性上的差别.壁面压力关联系数Rpp的等值线近似椭圆分布.椭圆的长轴为流向,短轴为展向.该分布说明压力关联的展向衰减比流向衰减要快.

图12 稳定对流区压力空间关联系数: 频率范围 ω0/(2π)∈[100,200] HzFig.12 Spatial correlation coefficients in the steady-convection zone: ω0/(2π)∈[100,200] Hz

进一步考察壁面压力空间关联衰减的定量性质.每个频率下,计算流向关联和展向关联的半衰长度,也即关联衰减到一半时的长度;然后对半衰长度和频率倒数的相关关系开展线性回归分析.图13 中展示基于了两种不同亚格子模型的大涡模拟的结果.从图中可以看出,稳定对流区内的壁面压力空间关联半衰长度,在流向和展向均和频率倒数成正比.带壁面修正的Smagrinksy 模型的结果中,流向空间关联半衰长度与频率倒数正比关系的线性相关系数为0.912,展向为0.731;流向和展向相关系数在WALE模型中的结果分别为0.961 和0.863.线性回归分析定量地证明了稳定对流区的空间关联衰减与频率的倒数成正比.文献[13,31]中湍流边界层壁面压力的实验研究也报告了这一规律.Corcos[13]基于该结论构造了相应空间关联模型.因此,通过基于空间关联的定量分析,发现稳定对流区内的壁面压力脉动具备平板边界层的时空特性.

图13 空间关联半衰长度与频率倒数的线性拟合Fig.13 Linear regression of the half-width of the spatial correlation and the inverse of the frequency

4 结论

本文基于可压缩大涡模拟方法,配合Smagorinsky和WALE 两种亚格子模型,开展了理想汽车后视镜绕流的数值研究.基于大涡模拟的时均流场,讨论了后视镜绕流的流动结构,并针对玻璃窗的壁面压力空间分布和时间历史开展谱分析,比较了该流动壁面压力波数频率谱与平板边界层的异同.最后基于泰勒冻结假设,得到了玻璃窗区域内的压力脉动对流速度的分布,并在特定区域内开展压力的谱分析和关联分析.本文的主要结论如下.

(1) 来流经后视镜在下游产生两个回流区: 后视镜顶部剪切形成的中部回流区和侧向剪切层形成的侧向回流区.其中侧向回流区引起的壁面压力脉动均方根较大.来流受后视镜阻挡后形成两个呈特定偏转角的尾迹.

(2) 下游紧贴后视镜的玻璃窗区域内,壁面压力波数频率谱按相速度可以划分为3 个不同分量: 声学分量、对流分量和回流分量.声学分量主要分布在低波数,高频率区域,其传播相速度介于±c∞+u∞之间;主对流分量的压力脉动相速度介于 0.375u∞～u∞之间;回流分量的压力脉动相速度介于-0.675u∞～-0.15u∞之间.壁面压力脉动空间谱中在零波数处呈山谷分布,与平板湍流边界层中Kraichnan-Phillips定理的结论一致.然而,空间谱等值线形状,相比于平板边界层,存在由后视镜下游展向流动引起的弯曲.

(3) 基于泰勒冻结假定,玻璃窗在物理空间中可按压力脉动对流速度分为3 个部分: 回流区、稳定对流区和过渡区.稳定对流区中,对流速度分布均匀,整体与流向形成偏转角.稳定对流区中,壁面压力波数频率谱仅有声学分量和对流分量,没有回流分量;壁面压力空间谱弯曲现象消失.该区域中的壁面压力空间关联在流向和展向的半衰长度均与频率倒数呈正比,与平板边界层壁面压力的空间关联具有类似的性质.