基于屈曲分析的大型搪瓷拼装钢罐外压失稳性能分析

黄承尧 杨 兴 李双喜 宋子峰 闫欣欣

（1.北京化工大学 流体密封技术研究中心；2.唐山盈和瑞环保设备有限公司）

大型拼装罐体的建造是基于圆筒薄壳理论［1］，采用变壁厚罐体设计，通过高强度螺栓将特制搪瓷钢板相互连接，层层拼装而成，最后用耐候密封胶将搪瓷钢板之间的连接缝加以密封，成为完整封闭的罐体。 搪瓷拼装钢罐具有特殊的现场拼装工艺和搪瓷防腐技术，使得拼装罐具有建造周期短、易扩容、耐腐蚀、后期维护运营方便、应用广泛的优点。

大型搪瓷拼装罐体的内压设计已有相对完善的设计标准，而罐体承受外压工况的情况国内外鲜有报道， 这就造成某些实际工程案例中，由于设计经验不足以及缺少相关的建造指导分析，时常出现搪瓷拼装罐体发生屈曲变形、螺栓失效的情况，造成罐体局部坍塌、罐体失效等问题［2，3］。20世纪70年代，西方发达国家利用先进的搪瓷工艺和设备，进行了搪瓷拼装罐的开发，并制定了相关建造标准。 国内虽然起步较晚，但科技革新促使有机复合材料不断突破，促进了国内大型搪瓷拼装罐的发展［4，5］。针对大型搪瓷拼装罐的结构研究， 唐修忠总结了大型搪瓷拼装罐体的发展，可为国内大型搪瓷拼装罐体的发展提供参考［6］。文献［2，7］基于ANSYS Workbench建立等效三维模型，改变不同膜顶储罐结构参数进行数值模拟分析，得出中心立柱高度对膜顶储罐的罐顶失效影响最大，同时提出失效修复方案，确定了最优中心立柱与顶部拉筋带角度设计，并通过自制的螺栓预紧传感器验证了修复方案的可行性；谭永明和王晓辉针对大型搪瓷拼装罐设计了一种独特的球顶结构，并采用ANSYS静力学模块和屈曲分析模块分析不同工况下罐顶的应变和屈曲极限应变［8］。在大型搪瓷拼装罐体安全监测方面，娄燕祯等基于超声波监测，研究搪瓷拼装罐的螺栓终拧后螺栓预紧力的损失变化规律［9］；周云双采用分布式光纤传感器建立了大型储罐的健康监测系统，并采用等比例模型进行虚拟试验数据研究，为大型储罐安全运行提供了监测手段［10］。

目前，国内的拼装罐体设计借鉴焊接罐的标准进行设计校核，为数不多的针对大型拼装罐的校核公式的计算结果的真实性也有待验证。 随着计算机仿真技术的发展，特征值屈曲分析和非线性屈曲分析仿真手段出现，利用数值模拟手段能够有效提高罐体设计的安全性和可靠性。 特征值屈曲分析即线性屈曲分析，通常需要对大型搪瓷拼装罐三维模型进行无缺陷假设，即忽略罐体的几何变形， 采用计算效率更高的线性迭代方程，数值分析结果能够有效预测罐体承受外压下的屈曲变形规律和极限载荷。 非线性屈曲分析考虑了罐体几何材料的非线性，采用弧长法基于一阶屈曲模态的临界载荷因子， 在模型施加微小扰动，求解罐体屈曲分析的平滑响应过程，得到的结果通常更接近实际。 笔者对搪瓷拼装罐进行数值模拟分析，在不同工况组合下探究搪瓷拼装罐体的屈曲变形，得出罐体在各种工况下的变形规律，并基于分析结果对经验公式进行校正，以期为拼装罐的屈曲设计提供指导。

1 大型搪瓷拼装罐的结构及承受外压原理

笔者选取了一个典型结构的大型搪瓷拼装钢罐（直径8.4 m、高8.4 m）作为研究对象，罐体主要由特制的搪瓷钢板通过高强度螺栓连接层层拼装而成，主要由罐顶、箍筋、抗风圈、地基、接管部件构成。 拼装储罐承受外压的结构原理如图1所示。

图1 大型搪瓷拼装储罐承受外压结构原理

拼装罐体的结构参数如下：

2 储罐屈曲分析模型建立

2.1 等效屈曲分析模型

实际建造过程中，搪瓷拼装罐体采用高强度螺栓将周围打孔的搪瓷钢板拼装连接，对罐壁成千上万的螺栓进行建模并进行屈曲分析显然不合适。 为了提高计算效率，基于4点假设将模型进行必要简化：

a.罐壁发生屈曲变形后螺栓仍处于许用强度之内；

b.钢板与钢板之间的连接缝隙密封良好无缺陷；

c.搪瓷钢板开孔后的抗变形能力与未开孔的搪瓷钢板呈线性关系；

d.罐体顶部部件及其相关附件能够通过等效力学关系施加于罐体之上。

综上，本次分析将模型视为一个无缺陷的等效圆筒搪瓷罐体， 其三维等效分析模型如图2所示。

图2 简化后的圆筒搪瓷罐体三维模型

实际工程中利用高模量密封胶能够有效保证罐体的密封性，故假设b成立；假设d通过仿真边界条件设置也能够实现；为了建立等效分析模型，下面对假设a、c进行验证。

2.1.1 搪瓷钢板等效关系

为了探究不同钢板开孔与无接缝、无开孔罐壁所能承受的外压等效关系，模拟分析两层钢板之间相互拼装在一起并考虑拼接接缝，建立搪瓷钢板两层栓接的1∶1模型和两层无开孔钢板的1∶1模型，如图3所示。

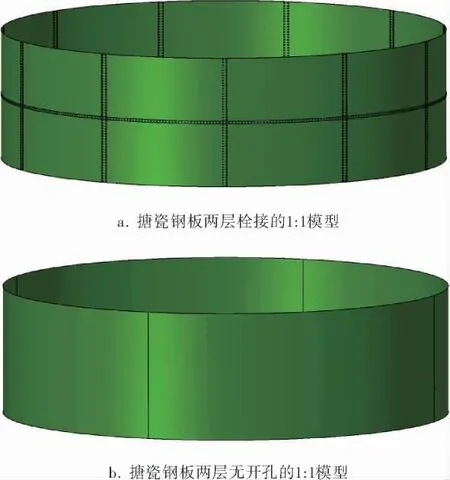
图3 搪瓷钢板分析模型

分别对不同厚度（6、7、8、9、10 mm）的钢板施加外压载荷750 Pa、 上下表面施加固定约束并进行屈曲分析，得出的临界载荷因子见表1。

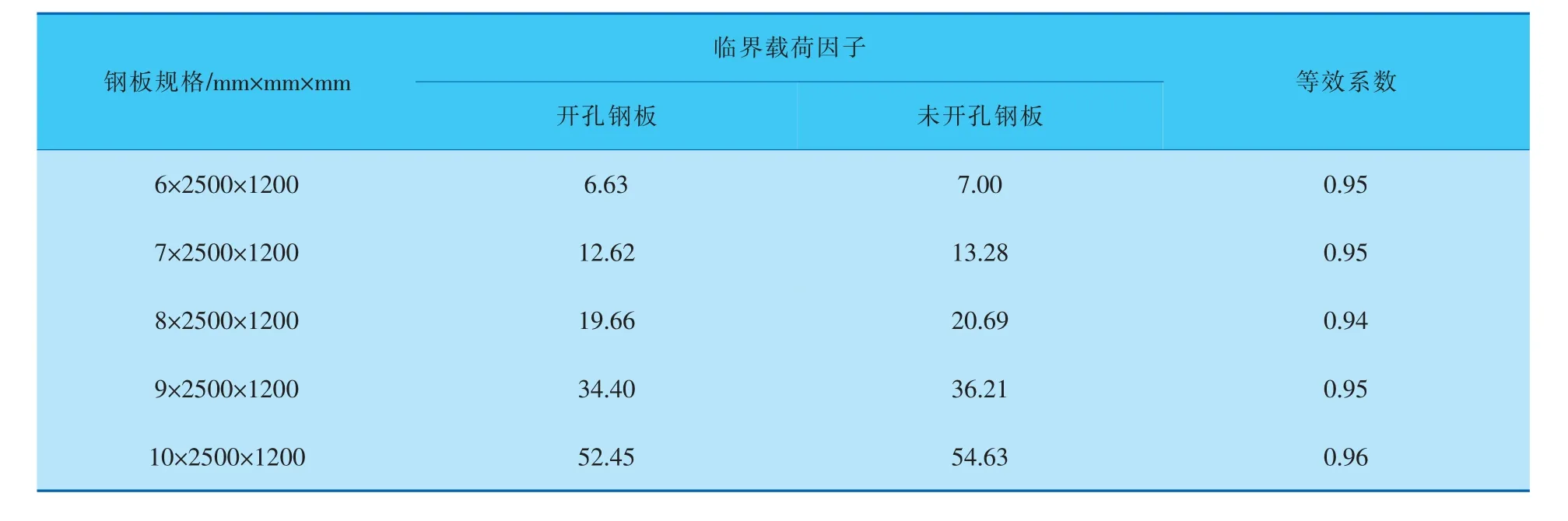
表1 开孔钢板与未开孔钢板的临界载荷因子及等效系数

从图4所示的开孔和未开孔搪瓷钢板不同板厚对应的临界载荷因子变化趋势可以看出，不同规格的钢板开孔与未开孔其临界载荷因子都存在着倍数关系，即实际罐体所能承受的极限载荷以该值为参考，定义为数值模拟解的95%，由此证明假设c成立。

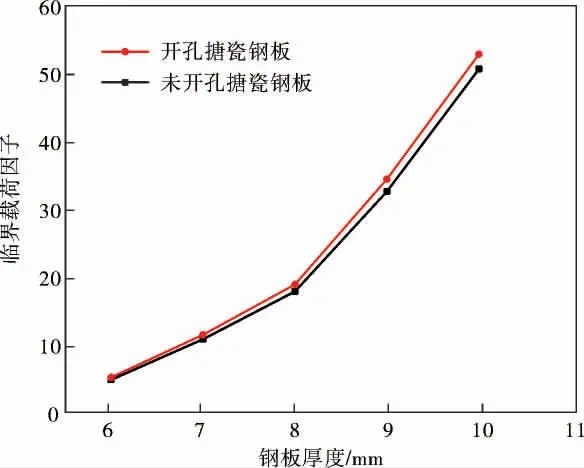
图4 不同板厚对应的临界载荷因子

2.1.2 极限载荷下螺栓的强度与刚度分析

等效罐体的建立不得不考虑螺栓的强度，通过表1的极限载荷因子与施加于壁板的外压乘积，可以求解不同规格钢板在相互连接状态下所能承受的极限载荷，基于该载荷取罐体的螺栓节点为研究对象并设置相应的边界条件，螺栓节点的分析模型如图5所示。

图5 螺栓节点分析模型

当搪瓷钢板发生屈曲变形时，极端事故发生时螺栓往往发生的是剪切破坏，故对模型两侧施加受外压载荷（表2）并求得螺栓所受的剪切力。

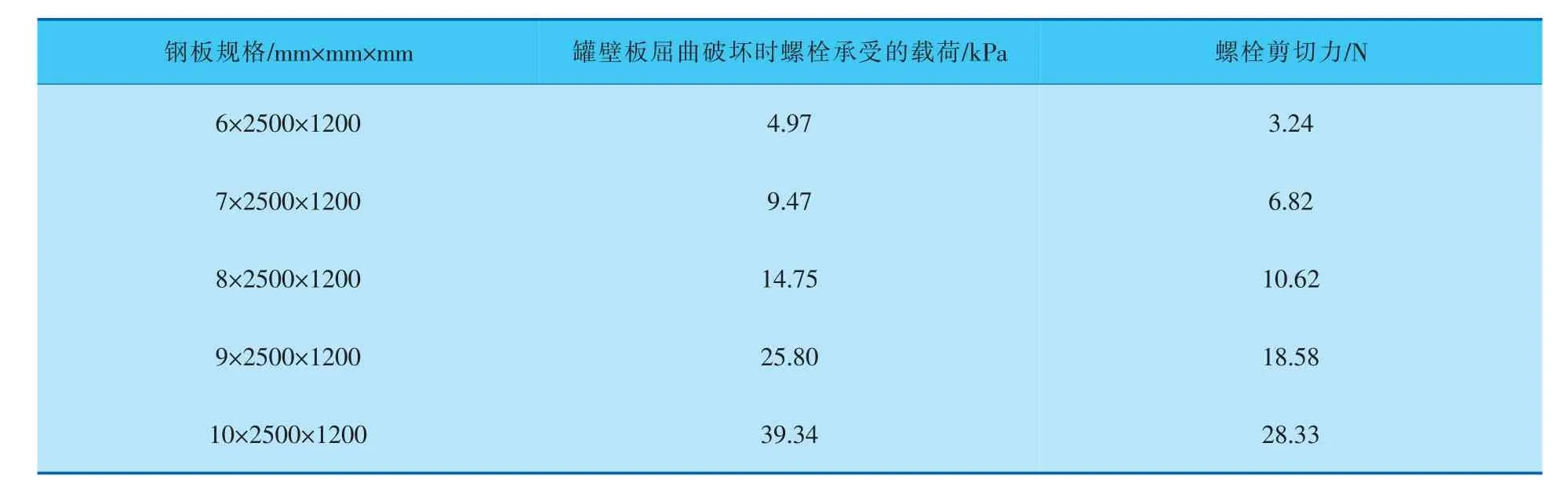
表2 搪瓷钢板发生屈曲变形时螺栓承受的剪切力

罐体建造采用的是高强度螺栓栓接，螺栓剪切力和有效面积通过查阅标准并根据剪切强度校核公式可以对螺栓的剪切力进行校核，具体公式如下：

可以看出， 当搪瓷钢板受到屈曲破坏时，螺栓所承受的剪切力τ远远小于许用值； 当钢板受到外压破坏时， 螺栓仍然处于正常服役状态，由此假设a成立。

2.2 储罐工况设置

结合实际工程案例和设计文件，将通过对表3的工况组合进行有限元屈曲分析， 并详细说明各种工况的边界条件与施加方式。

表3 分析工况组合

重力。 对整个罐体施加罐体轴向向下的重力加速度，将罐顶的部件通过附加重力形式施加于整个罐体。

液柱静水压。 在储罐内壁施加沿罐体轴向向下呈线性随高度变化分布的静水压， 介质密度1 000 kg/m3。

风载荷。 根据API 650标准中的风压设置标准， 风载荷在罐壁在0°罐体子午线的位置风压最大即为迎风侧，此时极限风压为p，沿着罐壁呈余弦函数分布在罐体两侧±90°的位置风压最小（0 Pa），如图6所示。

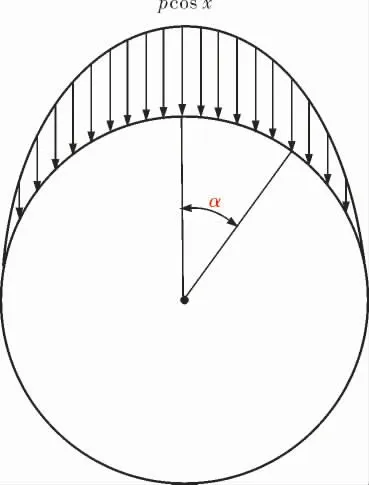
图6 风压分布示意图

在标准大气压下风压与风速可转换，即：

式中 v0——风速，m/s；

w——风压，Pa。

根据此法求解出临界载荷，可快速转换为风速，更为直观地为实际工程提供计算依据。

上述工况涵盖了所有大型搪瓷拼装罐的实际工程应用场合，下面将通过特征值屈曲分析得出罐体在各种工况下实际能够承受的最大极限载荷。

2.3 风载荷作用下罐体的屈曲分析

按照API 650标准对罐体施加边界风载荷，忽略风压在高度上的变化，分别探究罐体设置抗风圈与未设置抗风圈的极限屈曲值，空罐状态下罐体的屈曲变形失稳波数如图7、8所示。

图7 空罐状态的罐体带抗风圈屈曲模态

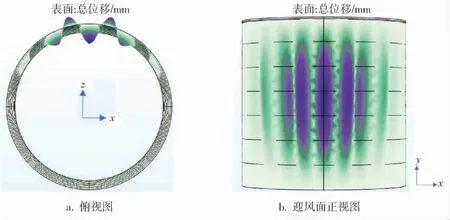
图8 空罐状态的罐体不带抗风圈屈曲模态

通过上述分析可以得出，有抗风圈罐体的极限屈服发生在罐体中部，即第2、3根抗风圈之间，且极限值位于罐壁子午线及0°的位置，临界载荷因子为11.762，失稳波数为3，此时的临界载荷为11.762×750×cos 0°=8.82 kPa， 将该极限载荷由式（1）转化为风速约为137 m/s。 无抗风圈罐体发生屈曲变形的趋势与有抗风圈的罐体大体相同，但是发生屈曲坍塌的面积扩大，此时的临界载荷为3.949×750×cos 0°=2.962 kPa， 将该极限载荷由式（1）转化为风速约为68.8 m/s。

不同高度的风压对罐体屈曲变形的影响。 工程上，为了方便计算分析，通常会忽略风压在高度上的变化对罐体施加等效载荷，然而依据风载计算公式，有：

式中 I——风重要因子；

KZ——在投影面积的质心高度Z处评估的速度压力曝光系数；

qZ——风载荷，Pa；

V——基本风速，m/s。

结合美国水工业标准， 当罐体的高度超出15.2 m，速度压力曝光系数KZ（影响最大风压的系数）会随之提升，具体的曝光系数见表4。

表4 速度压力曝光系数

因此，需对不同高度的位置施加不同风压系数，使计算结果更具有真实性。

本节以实际工程案例计算的φ11.7 m×24 m罐体设计结果作为分析对象，罐壁壁厚（自下而上）11、10、10、9、9、8、8、7、7、7、6、6、5、5 mm、其余4 mm时， 每隔2.4 m设置一道抗风圈100 mm×63 mm×6 mm； 试验组与对照组的重力加速度均取值9.81 m/s2；风压在不同高度的设置见表5。

表5 对比试验工况设置

按照网格划分以及施加相应的边界条件得出的分析结果如图9所示，可以看出，对照组与试验组罐体发生屈曲变形趋势及最大变形位置有所区别， 但是大体的变形规律以及发生屈曲变形的位置基本一致， 对照组的临界载荷因子为8.4， 对 应 的 极 限 外 压 载 荷 为8.26×750×1.165=7.22 kPa；而不考虑风压高度变化的试验组临界载荷因子为9.63， 对应的极限外压载荷为9.78×750=7.34 kPa。

图9 φ11.7 m×24 m分析对比结果

从上述数据可以看出，风压随高度的变化对罐体的极限外压载荷很小。 为了验证这一结论，通过设计文件对φ12.99 m×18 m、φ15.28 m×24 m的罐体按照上述边界条件设置进行分析计算，屈曲变形云图分别如图10、11所示， 计算结果汇总见表6。

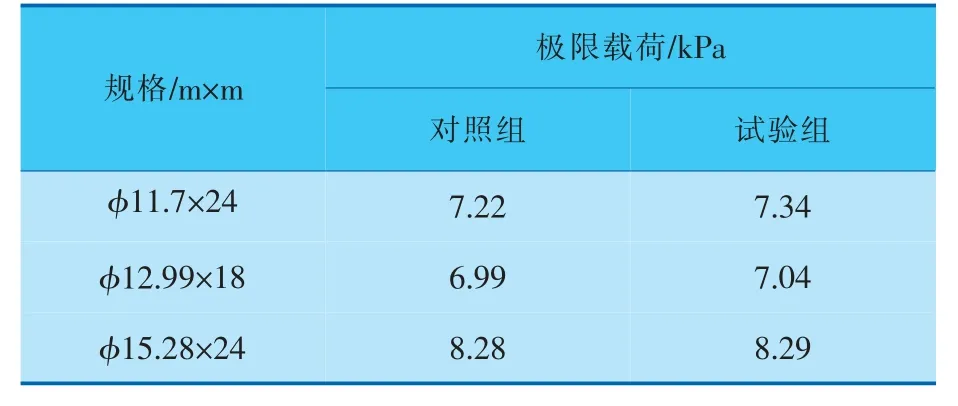
表6 对照组、试验组极限载荷计算结果汇总

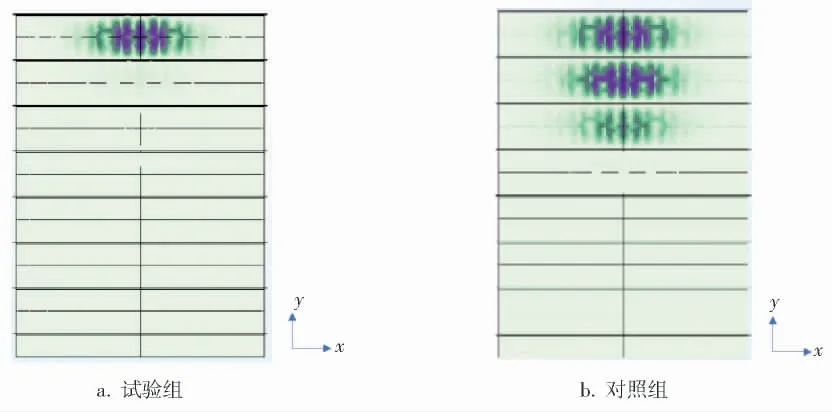
图10 φ12.99 m×18 m屈曲变形云图

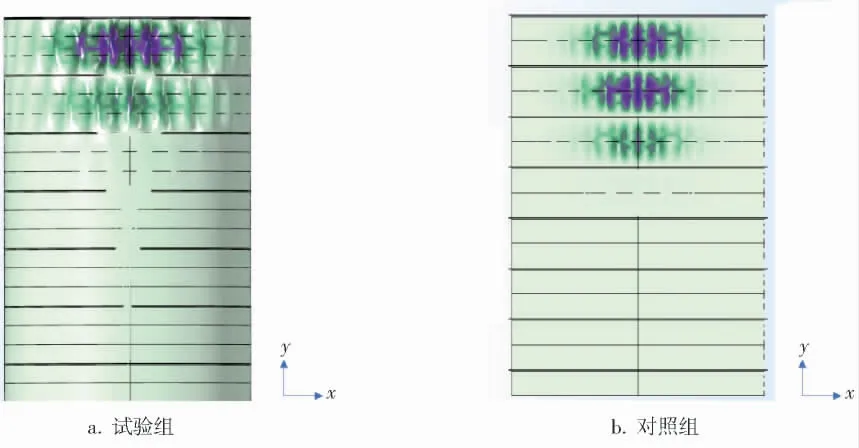
图11 φ15.28 m×24 m屈曲变形云图

通过上述分析可以看出，罐体的外压极限载荷与风载荷在高度变化上关系很小，罐体所能承受的外压载荷与罐体本身的特性息息相关，故在进行罐体设计时可以忽略风压在高度上数值的变化，以此方法进行罐体设计在提高计算效率的同时仍然能够保证罐体安全。

2.4 内压、风载荷共同作用下罐体的特征值屈曲分析

通常在静水压状态下，罐体能够承受更大的极限载荷。 现将通过对罐内不同高度的静水压同时承受外界风载荷共同作用的边界条件下对罐体进行屈曲分析，结果如图12～14所示。

图12 介质满罐（静液柱高8.4 m）状态下的屈曲模态

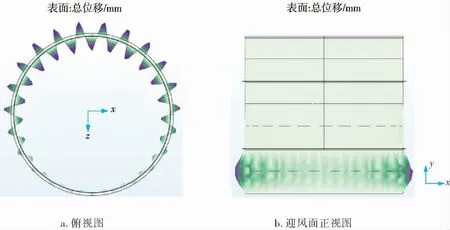
图13 静液柱高6.0 m状态下的屈曲模态

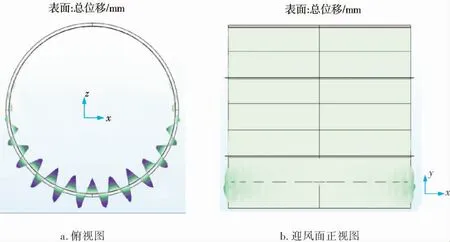
图14 静液柱高2.4 m状态下的屈曲模态

通过对罐体内储存不同液位高度的介质并承受外部风载荷的实际工况下，对罐体进行屈曲模态分析可得罐体载荷因子及其对应的极限载荷见表7。

表7 不同静水压高度下罐体对应的载荷因子及极限载荷

通过上述分析可知，罐体内部存在介质能够提高罐壁的极限屈曲载荷，栓接罐体内部存在介质能够提高罐体的极限屈曲载荷，这个值随着罐内介质高度的降低而降低，满罐与空罐所能承受的计算载荷相差约两倍。 另外，通过观察云图可以发现， 外部风载荷与内部静水压相互作用，罐体的屈曲发生在背风侧，并且发生屈曲变形的位置位于罐壁底层抗风圈与地面之间。

3 经验公式修正

为了寻找外压搪瓷拼装罐的经验计算公式与数值仿真模拟结果的线性关系，并对经验公式进行校正， 考虑罐体缺陷并基于屈曲分析结果，采用非线性屈曲分析计算出几种罐体规格对应的屈曲分析结果， 并将不同方法求解进行对比。利用等效分析方法将经验公式计算结果与仿真结果进行对比并计算得到的偏差见表8。

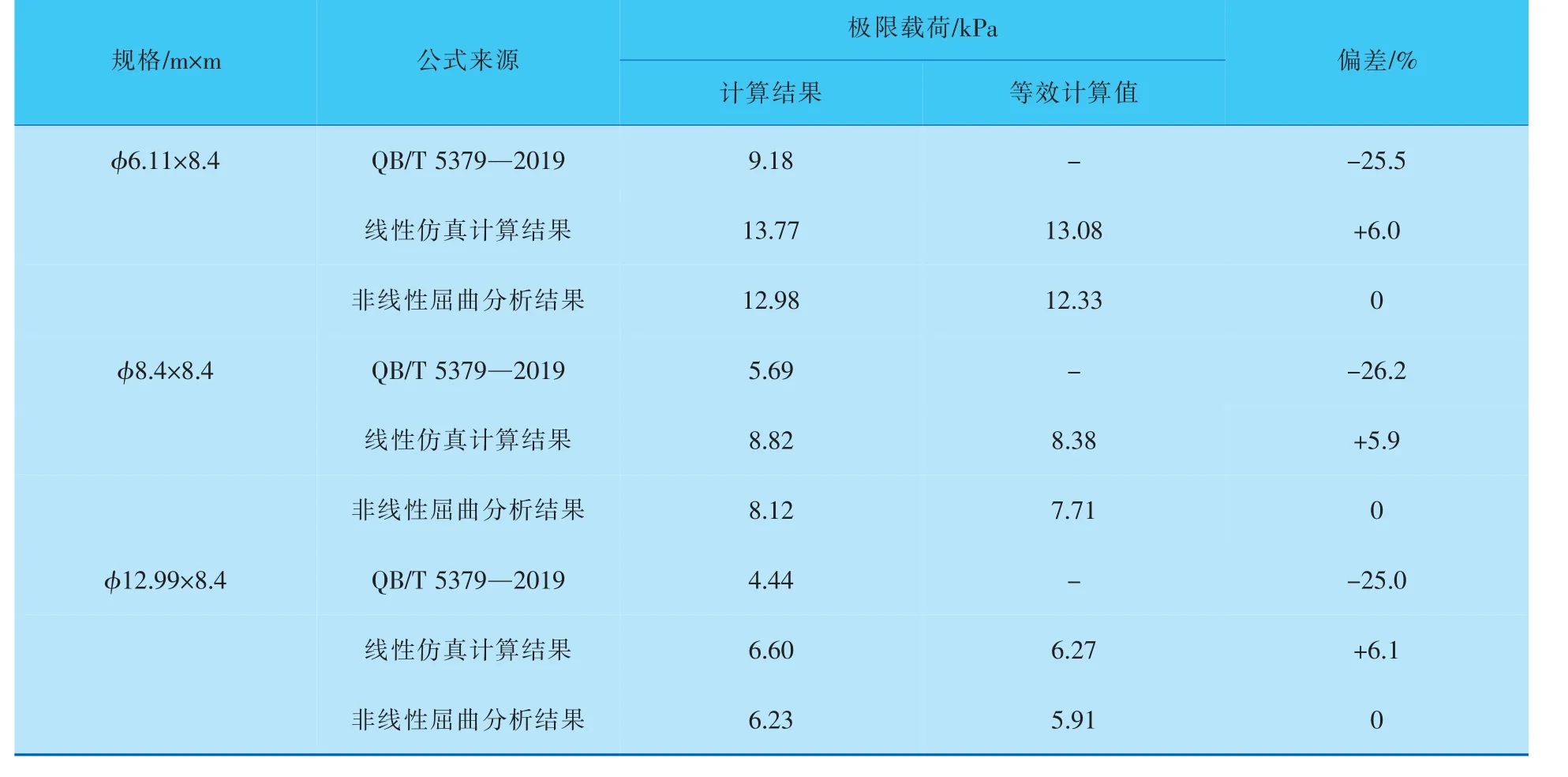
表8 不同计算方法得出罐体的极限载荷值及偏差值

对比上述数据发现：屈曲仿真分析结果高于经验公式的外压计算结果，偏差值在±25%浮动；而考虑了罐体缺陷的非线性屈曲分析与线性屈曲分析结果的偏差在±6%。 通过公式计算的各项参数，在经验公式中考虑了影响罐体变形的重要因素：壁厚、罐径、抗风圈安装位置、罐高，考虑全面，利用经验公式指导罐体设计合理可行，但计算结果与仿真分析研究结果相较偏于保守，建议经验设计公式取计算结果的1.25倍。

4 结论

4.1 在相同载荷下， 开孔板与未开孔板在相互拼装的状态下，发生最大屈曲变形的位置及变形趋势基本一致，若要计算开孔搪瓷钢板的极限屈曲载荷,可取未开孔钢板的95%。

4.2 在承受外压的状态下,螺栓主要承受剪切且远小于螺栓的许用值，通过数值模拟，相较于其他服役工况，罐体在空罐状态下最容易受到外压载荷造成屈曲变形。

4.3 罐体最危险的工况是罐体处于空罐状态下，且承受外界风载荷容易导致罐体发生屈曲变形。对于承受风载荷发生变形的原因主要是风载荷引起的，发生形变的位置主要分布在迎风面±60°附近，其中0°位置是屈曲最严重的位置，沿着两侧递减。

4.4 罐体所能承受的极限外压与罐体的板厚、抗风圈安装位置、罐体直径、搪瓷钢板材料强度有较大关系，因此利用经验公式和仿真计算式可以忽略风压在高度方向的变化，并且经验公式计算结果偏保守，利用经验公式进行罐体设计可取计算值的1.25倍。