应用裂缝-油藏耦合技术的油藏水井压裂参数优化数值模拟

李庆庆 王国丞 孙 爽 鲁世君 王 舸

（长庆油田分公司第五采油厂采油工艺研究所）

如果地质条件适合开采矿藏资源，施工难度就会大幅度下降，施工条件也会明显变好，采集得到的油中水的比例也会随之上升。 为了保证增加石油开采的产量，会在这些石油矿藏区域内施行裂缝-油藏耦合技术， 参数的不同会极大程度地影响技术实施的成功率。 为降低工程风险和工程实施的难度，需要对其进行数值模拟，并优化相关参数。

在现有的油藏开采方法中，文献［1］根据室内实验与矿产资料的数据，以定量定性的时变规律为核心，得到了一个基于驱替通量的石油开采数值模拟方法，在概念模型中，可以分析不同的参数对开发效果的影响，并保证储层的油量分布不会降低含水量的调控策略。 文献［2］需要通过油藏的储层参数进行油水位移分布的测试，在空隙网络中得到碳酸盐样品的模型参数，并分析孔喉结构下的渗流模型，在水驱油藏开发中，实现储层物性的变化， 并依据具体的模型进行计算。文献［3］是一种以有限元法为核心的混合数值离散化耦合模拟方法，将矿场数据作为偏差值的流动特性，将动态裂缝的致密性水力压裂动态信息进行了全隐式的求解，在忽略模型压力与渗流环境的条件下，保证双孔应力的隐式表征，完成对产能的改变模拟实验。

笔者结合以上文献， 设计了一种应用裂缝-油藏耦合技术的油藏水井压裂参数优化数值模拟方法。

1 基于裂缝-油藏耦合技术设计油藏水井压裂参数优化数据模拟方法

1.1 计算油藏水井压裂应力

通过渗透力可以改变径向流变的流动能力，在原生裂缝与次生裂缝中存在一定的时间区别，作为构造裂缝的主要动力［4］。 需要首先分析油藏水井裂缝的3种主要方式（图1）。

图1 油藏水井裂缝形式

如图1所示，在这3种裂缝中，开口型的破裂主要是由于两个正反方向的相互作用力的影响，是一种张性的开裂现象；滑动型裂缝则是由于正反两个方向的相互作用力导致的滑动位移，是一种剪切破裂的天然裂缝；撕裂型裂缝同样是张性裂缝，但是其剪切滑动的力相对较大，并且力的方向并不是正好相反［5，6］。依据这3种裂缝方式，可以得到井壁周边的孔道主应力，应力的计算公

式为：

其中，F1和F1′分别为井壁处受到一个方向的力与受到其反向的力；F2表示射孔位其中一个方向的力，F3表示一定夹角后另一个方向的力；α1和α2则表示轴向的最大与最小应力［7］。 此时可以计算开口型、滑动型和撕裂型3类应力Fk、Fh、Fs：

式中 dp——摩擦系数；

fp——孔道周边流体压力；

Hi——地层倾角；

mk——裂面余弦；

ni——主应力方向夹角［8，9］；

pi——泊松比；

Yn——垂向地应力；

αn——主应力的最大夹角；

γi——多空弹性系数；

ηn——弱面黏聚力；

δmax——压裂的最大开裂压力。

1.2 基于裂缝-油藏耦合技术建立油藏流体等效模型

使用有限体积法进行微分控制方程的离散处理，在六面体的控制单元中，可以单独设置一个单元的中心点（图2）。

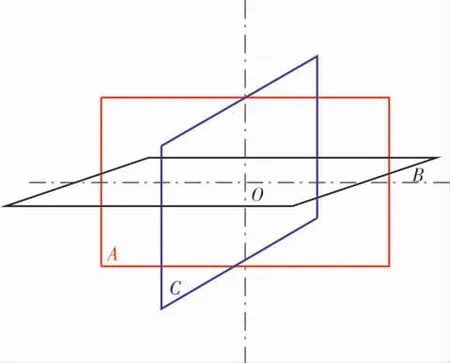
图2 控制单元结构图

如图2所示，在单元结构模型中，有1个中心点O，3个平面A、B、C分别穿过点O，并将其作为自身的中心点［10］。 在网格计算中，同样可以将不可压缩的黏性流体移动到管道中，在考核耦合作用的同时，将其与运动学条件相融合，得到法向速度的连续方程：

式中 dq——单位应力矢量分量；

fn——流体流动界面中的耦合交界处的法

向速度；

up——交界面的单一速度分量。

在描述内力场应力的过程中，将基础物理量作为一个应力矢量，可以得到基线方程为：

式中 pn——外域对内域的应力场矢量；

Δd（f）——物体内域和外域的外部法线矢量；

Δpi——微元体的平衡参数。

此时可以得到通过表层进入带空间的湿液变化方程的平均渗流速度vm为：

式中 np——任意形状的点位价态［11，12］；

nt——参照模型的等效骨架材料系数；

Vs——岩石参照构型的体积；

ρm——水流密度。

在这个公式的基础上，可以将油藏水井中压裂的耦合技术转换为流体的数学模型，并进行不同单元结构的划分，形成应力平衡下某单元有限元方程的格式矩阵，最后构成油藏流体的等效模型。

1.3 设置边界条件

在压裂机理中，起裂与延伸是两个不同的方向，因此可以将水井的压裂缝隙分为横向裂缝与纵向裂缝， 在计算裂缝长度与裂缝宽度的过程中，将地层破裂时井底的延伸压力转化为压裂施工的地层压力，即可得到破裂的压力曲线（图3）。

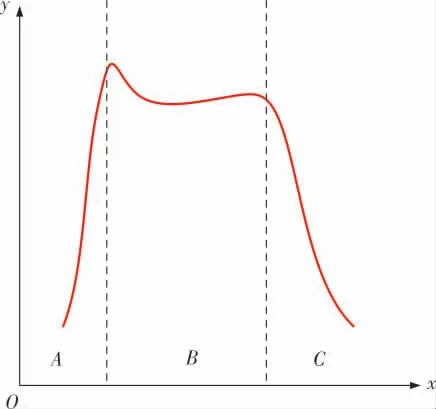
图3 油藏水井压裂的应力曲线

图3中横坐标为时间， 纵坐标为单位时间内的压力。 在油藏水井压裂的应力变化中，主要分为3个部分：A段内的破裂压力， 此过程中井底压力达到最大值时，破裂压力也为油藏水井压裂应力的最高点；B段主要是对油藏水井压裂延伸压力的扩展，此过程基本是一个水平直线，代表应力发生的变化幅度较小，基本没有变化［13，14］；C段是地层压力的减少步骤，此过程如图所示，应力会逐渐变小，直至与初始位置平衡。 依据此过程会直接得到有限元模型的边界条件，在下表面施加垂直方向的位移约束时， 可以模拟下部地层，对计算模型进行约束与分析。 并结合上表面的压力荷载定理，得到模型内部重力荷载、受力荷载等的初始应力。 最后在连续性方程、动量方程的基础上， 保证流体在平衡板切面上的流动特性，基于幂律流体的本构方程，得到剪切应力的稠度系数， 最终实现沿裂缝方向梯度压力的变化表达， 得到基于裂缝-油藏耦合技术的油藏水井压裂参数优化数值模拟的边界条件。

2 实验研究

2.1 建立有限元模型

将某油井的储油层作为本次实验的研究对象， 以测试文中设计的数值模拟方法的有效性，并获取更好的参数。 将计算模型中的最大主应力作为预测裂缝的方向，在压裂层中选择最初的单元制定解决方案，然后保证初始裂缝的水力油藏压裂流量， 通过瞬态分析的方法模拟裂缝状态。依据测试结果，设定油藏水井压裂的弹性模量为28.46 GPa，泊松比为0.37，初始地接应力为25.6、30.7、16.8 MPa，孔隙压力为14.3 MPa，孔隙度为0.145。 因此可以在这些参数的基础上，建立一个半径为0.01 m的几何模型， 得到油藏水井压裂的有限元模型如图4所示。

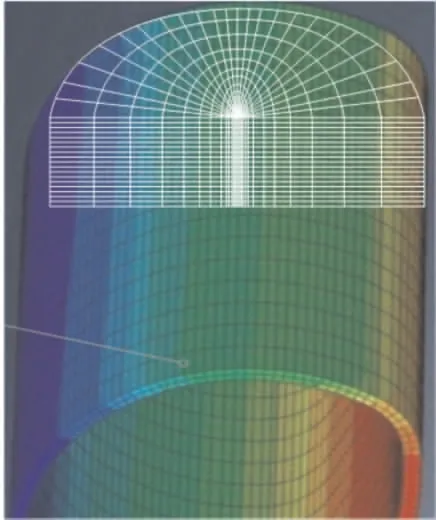
图4 油藏水井压裂的有限元模型

如图4所示，在一定半径、一定高度的圆柱形模型上划分单元结构并设置边界条件。 在模型中，假设地层岩缝中岩石的同性均质弹性体具备一定的网格条件，且井网布井方式通常采取五点法［15，16］。 使用ABAQUS软件划分地质体模型中的加密部分，在不同的步骤中，设置施工时间与累积量，以求取前置液的比例和平均砂比，得到的结果见表1。

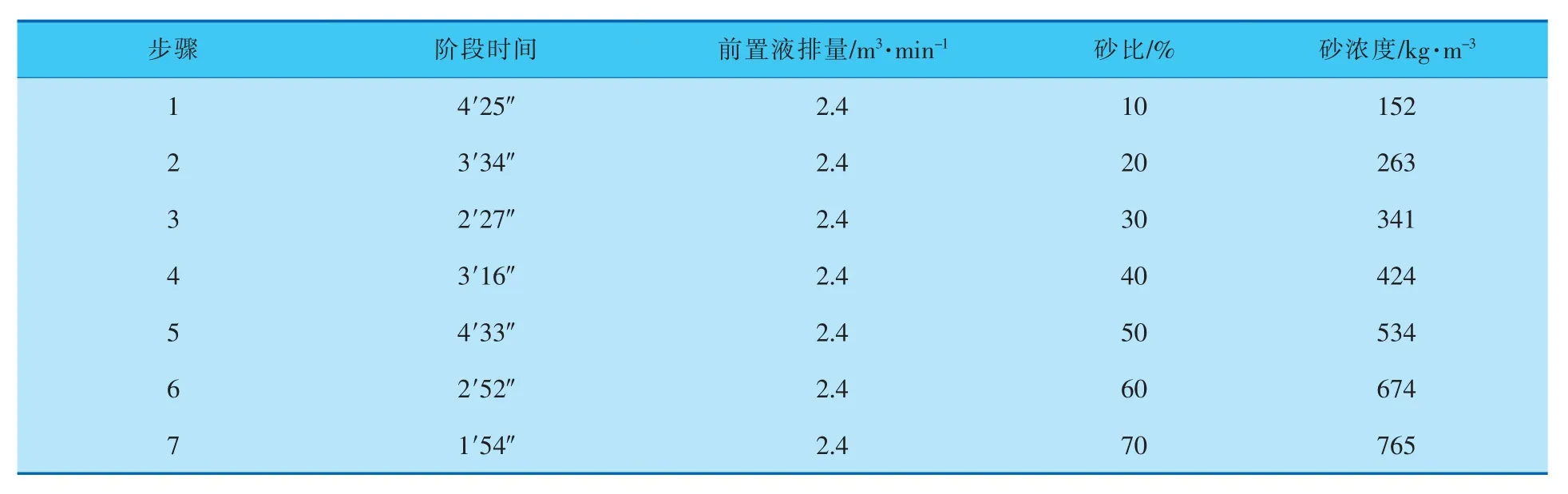
表1 前置液的比例和平均砂比

整理表1中的数据，可以得到7个阶段总共所需的施工时间为23′1″，平均砂比为40%，前置液比例约为36%， 此时可以进行水力压裂的数值模拟计算。

2.2 影响油藏水井压裂的参数分析

为研究不同参数对油藏水井压裂的影响，分别就压裂液黏度、压裂液注入量、支撑剂用量对所产生的裂缝长度与裂缝宽度的影响进行分析。

如图5所示，随着时间的流逝，裂缝长度与裂缝宽度均呈现增加的趋势，且压裂液黏度的变化对裂缝长度与宽度均会产生一定的影响，当压裂液黏度增加时， 裂缝长度的变化与其正相关，但是裂缝宽度的变化趋势则与其负相关。

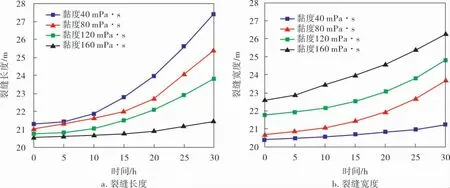
图5 压裂液黏度对裂缝尺寸的影响

如图6 所示，当压裂液注入量分别为2.4、2.6 m3/min时， 对裂缝长度不会产生过多的影响，但是当压裂剂注入量增长为2.8、3.0 m3/min时，裂缝长度与注入量成正比；而裂缝宽度的变化则与之不同，当压裂剂注入量为2.6 m3/min时，裂缝宽度变化的速度达到最大。

图6 压裂液注入量对裂缝尺寸的影响

如图7所示，当支撑剂用量为1、2 m3时，对裂缝长度的变化有一定的正向变化，但是当支撑剂用量到达3、4 m3时， 裂缝长度不会因支撑剂用量的增加而产生变化。 在裂缝宽度的测试中，支撑剂用量基本不会对其产生影响。

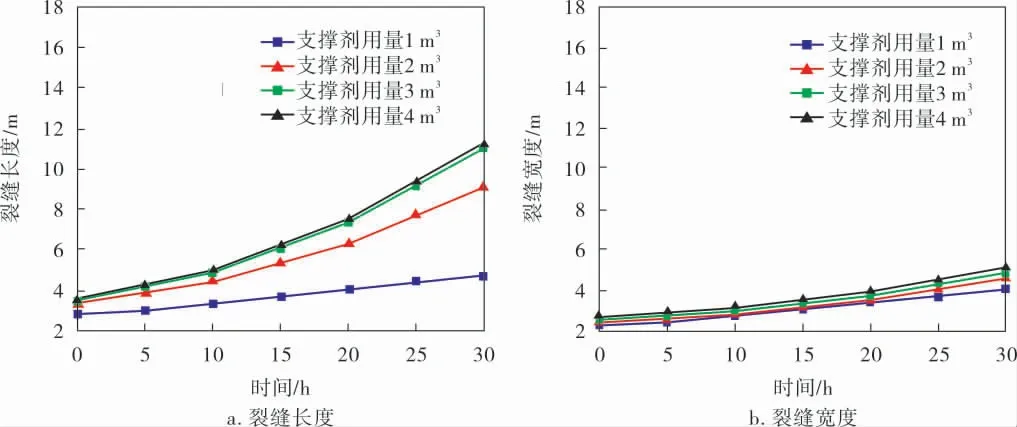
图7 支撑剂用量对裂缝尺寸的影响

3 结束语

笔者设计了一种裂缝-油藏耦合技术的油藏水井压裂参数优化数值模拟方法，为保证裂缝长度和宽度均达到理想状态，在建立了有限元分析模型后，对压裂液黏度、压裂液注入量和支撑剂用量进行分析，并得到其最优参数。 通过实验结果可知， 裂缝长度的变化与压裂液黏度呈正相关， 裂缝宽度的变化与压裂液黏度呈负相关，表明压裂液的黏度对控制裂缝形成和扩展具有不同影响； 当压裂剂注入量增长为2.8、3.0 m3/min时，裂缝长度与注入量成正比，当压裂剂注入量为2.6 m3/min时， 裂缝宽度变化的速度达到最大，表明在一定范围内，适当增加压裂剂的注入量可以有效地增加裂缝的长度，实现期望的裂缝宽度变化；当支撑剂用量为1、2 m3时，对裂缝长度的变化有一定的正向变化，但是当支撑剂用量到达3、4 m3时， 裂缝长度不会因支撑剂用量的增加而产生变化，表明在一定范围内增加支撑剂的用量可以对裂缝长度产生一定的正向变化，但一定范围内的支撑剂用量变化对裂缝宽度影响较小。 超过一定数值后，进一步增加支撑剂用量对裂缝长度和宽度没有显著影响。 通过文中的数值模拟方法，可以大幅度节省计算资源，并得到相同效果的等效模拟程度， 该方法对于处于中后期开发、水力压裂程度较大的油藏矿井具备较为实用的应用前景。