高海拔地区水力旋流器旋液分离过程CFD模拟与结构优化
2023-10-27王晓静张靖媛
王晓静 张靖媛
(天津大学化工学院)
我国青海地区有一百多个盐湖, 其中的钾、钠、镁、锂、碘、铯等矿产资源可以被用于多种工农业场合。 据统计,我国察尔汗盐湖地区氯化钾储量高达1.45亿吨,占全国储量的97%,目前该地钾肥年产量占国内市场40%以上[1~3]。 然而我国现有钾资源仅可利用不到70年[4],受到资源储量和开采程度的限制,到2020年察尔汗盐湖地区已不适宜继续扩大柴达木东部钾资源的开采量[5],因此改进生产过程是提高钾盐提取率的必然选择。目前, 察尔汗盐湖地区有多种钾肥生产工艺,包括反浮选-冷结晶法、冷分解-正浮选法,兑卤-控速结晶工艺等[6,7]。 在钾肥的生产过程中,氯化钾冷结晶器会产出带有氯化钾晶体微粒的冷结晶器溢流液,分离出这些晶体微粒是提高氯化钾产率的新思路。 首先回收氯化钾微粒可以直接增加收率, 其次分离出的细晶还可投放回结晶器内,作为晶核促进结晶过程的进行,因此回收氯化钾结晶具有很高的价值。 针对该问题,提出使用水力旋流技术来进行氯化钾冷结晶器溢流液的浓缩回收。
多年来,科研人员对水力旋流器的工作原理进行了深入研究。 CHU L Y等通过设计正交实验研究了结构改造对水力旋流器性能的影响,开发了一种带有翼形核心的新型水力旋流器[8,9];LIU Y C 等对三相水力旋流器结构提出了改进建议[10];王立洋等对液-液水力旋流器的分离效率与进口流速、油组分浓度、旋流器级数之间存在的关系进行了研究[11];刘永平等分析了粒径分布和结构尺寸对旋 流器分离性能的影响[12,13];刘培坤等提出了一种新型可调底流口旋流器[14];NARASIMHA M等使用LES湍流模型对水力旋流器进行了多相流数值模拟,并用伽马射线析像验证 了 模 拟 与 实 验 的 相 似 度[15];MURTHY Y R和BHSDKAR K U模拟了水力旋流器的固-液分离过程,得出了切割粒度随旋流器结构变化的规律[16];XING L等利用CFD-PBM方法研究了入口形式对液-液旋流器分离性能的影响[17]。 随着CFD技术的发展,利用数值模拟方法调整各项结构参数是水力旋流器结构改进的大势所趋。
笔者使用CFD技术研究了水力旋流器结构参数与操作参数对其流动特性和分离性能的影响,并给出了优化结果。 在计算过程中,特别考虑了青海察尔汗盐湖作为高海拔地区具有特殊的地理条件,将当地大气压与重力加速度作为初始条件代入计算。
1 水力旋流器
1.1 工作原理
水力旋流器是生产中最常用的分离设备,具有结构简单、占地空间小、运行平稳的优点。其分离原理为利用物料高速旋转产生的离心力场使存在密度差的物料沿径向分离, 在水力旋流器运行稳定后,旋流腔内产生内外旋流,轻相随着内旋流从上部的溢流口流出、 重相随外旋流从底流口流出,其内部流动过程示意图如图1所示。
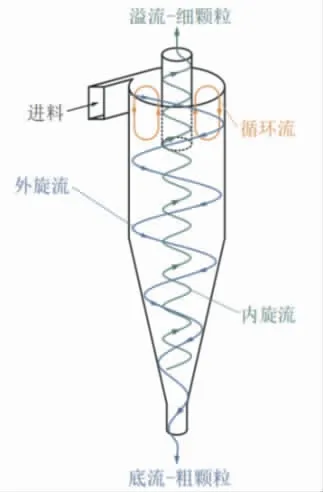
图1 水力旋流器内流体流动示意图
1.2 水力旋流器结构参数
直筒段筒径Dc是影响水力旋流器分级粒度的主要因素,筒径越大,分级粒度越粗。 氯化钾冷结晶器溢流液中的氯化钾颗粒粒径在0~100 μm之间,经查阅水力旋流器设计标准,发现筒径为150 mm时分离粒径一般在30~74 μm之间, 筒径为200 mm时分离粒径一般在30~100 μm之间,筒径为250 mm时分离粒径一般在40~100 μm之间,这3种水力旋流器均可满足项目分离要求。 水力旋流器其余部分尺寸参数一般按照通用标准旋流器进行选择:
a.入口直径为(0.15~0.25)×Dc;
b.溢流口直径为(0.2~0.3)×Dc;
c.底流口直径为(0.07~0.10)×Dc;
d.溢流管插入深度为(0.5~0.8)×Dc;
e.柱段长度为(0.7~2.0)×Dc。
本研究所用水力旋流器模型结构如图2所示,具体结构参数见表1。
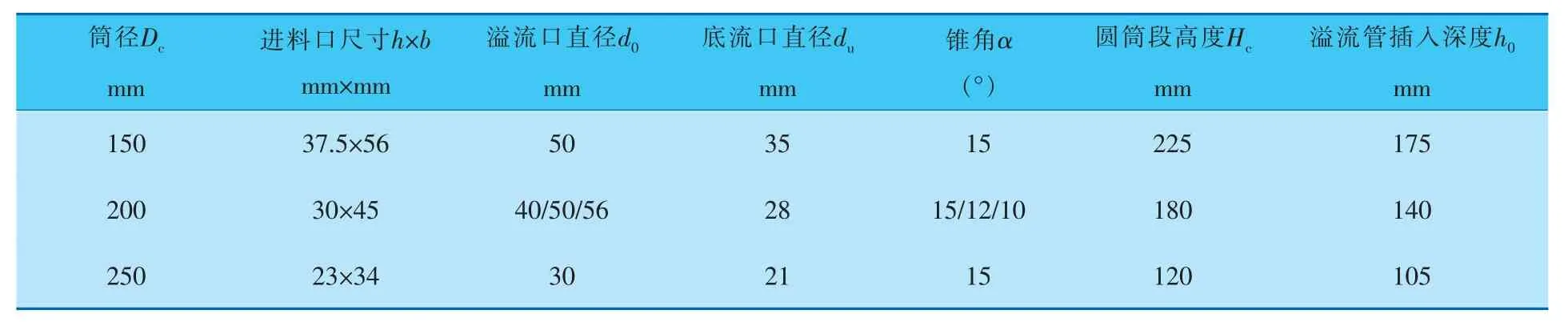
表1 水力旋流器尺寸参数

图2 水力旋流器几何模型
2 模型建立及网格无关性验证
2.1 计算模型设定
CFD计算中常用到的多相流模型有VOF模型、Mixture模型和Eulerian模型。 通常VOF模型被用于模拟两相及以上互不相融流体的流动过程,Mixture模型与Eulerian模型均可被用于解决含有离散相的多相流问题, 其中Eulerian模型虽然计算精度高,但计算过程过于复杂,对计算机性能要求较高, 故文中计算采用Mixture多相流模型。
合理选择湍流模型可以提高计算结果的准确性。 k-ε模型是目前应用最广的湍流模型,但其推导过程基于各向同性的涡黏性假设,在预测各向异性的复杂湍流流动时会有较大的误差,RSM模型摒弃涡黏性假设,直接求解雷诺应力微分方程,能更好地预测水力旋流器内复杂的各向异性流动过程,因此本文预采用RSM湍流模型。
2.2 边界条件及介质物性参数
计算使用3D模型,采用瞬态双精度求解器及SIMPLE压力速度耦合算法,入口条件设置为速度入口,溢流口和底流口均设置为压力出口,出口直接连通大气, 对流项分别采用PREETO! 与QUICK格式进行离散,壁面采用非滑移条件。
在氯化钾冷结晶器溢流液分离过程CFD模拟中,设置的物性参数如下:
a.连续相为饱和MgCl2溶液,密度1 180 kg/m3,黏度0.002 Pa·s。
b.离散相为KCl晶体颗粒,粒径在0~100 μm之间,其密度为1 980 kg/m3,质量分数为10%。
c.高海拔地区下重力加速度为9.786 m/s2,大气压强为72.4 kPa;平原地区重力加速度为9.810 m/s2,大气压强为101.325 kPa。
2.3 网格独立性验证
用Solidworks对水力旋流器三维建模后导入Mesh软件进行非结构化网格划分。 为减小网格数量对计算精度的影响,在正式模拟计算前需要对网格数量进行独立性验证。 因流量对网格数量变化较为敏感,故以Dc=200 mm、d0=40 mm、入口速度为5 m/s的计算模型为例,对在不同网格数量下水力旋流器流动过程进行CFD数值模拟, 并将所得溢流流量与底流流量的变化趋势进行对比,结果如图3所示。

图3 网格独立性验证结果
可以看出,网格数量达到58万之后,溢流流量与底流流量与网格数量为200万时极为接近,说明此时网格数量满足计算精度要求,因此选择网格数量为58万。
3 结果分析
3.1 公式计算
水力旋流器对固相的分离效率Es定义为底流口固相质量流量与入口固相质量流量之比,即:
式中 Mi——入口的固相质量流量,kg/s;
Mu——底流口的固相质量流量,kg/s。
压降Δp为水力旋流器入口与出口压力之差,即:
式中 pi——入口压力,MPa;
po——出口压力,MPa。
3.2 直筒段筒径选择
首先需选择适宜大小的直筒段筒径用于优化计算,在入口流速为5 m/s的条件下对筒径分别为150、200、250 mm的水力旋流器的分离过程进行模拟, 所得分离效率与KCl晶体粒径之间的关系如图4所示。可以看出,筒径为200 mm的水力旋流器对粒径在100 μm以下颗粒的分离效率高于其余两种, 原因是Dc=200 mm的水力旋流器内部离心强度高于Dc=250 mm的水力旋流器, 所以对固定粒径颗粒的分离效率更高,原本Dc=150 mm时离心强度最高、分级粒度最小,但5 m/s的入口流速对150 mm 的水力旋流器来说过高,所以30 μm以下的颗粒还没来得及被分离就已经从溢流口离开旋流器, 导致其分离效率反而低于Dc=200 mm的水力旋流器,由此可以看出Dc=150 mm的水力旋流器的明显缺点是处理能力较小。 综上分析, 采用200 mm的水力旋流器用于模拟工作。由图4看出,Dc=200 mm时水力旋流器对40 μm以上的颗粒分离效率接近100%,所以为清晰地看出各项结构参数对分离效率的影响,后续模拟工作只分析各项参数对10~50 μm粒径范围内颗粒分离效率的影响。
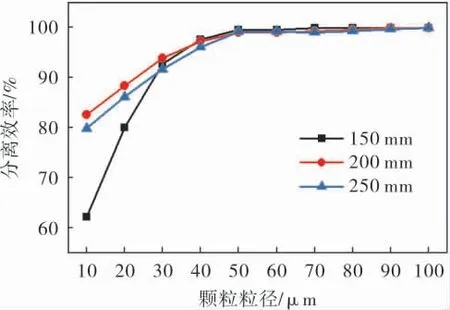
图4 不同筒径下水力旋流器的分离效率
3.3 溢流口直径对水力旋流器性能的影响
在入口流速为5 m/s的条件下对溢流口直径分别为40、50、56 mm的水力旋流器的固-液分离过程进行CFD数值模拟, 并在圆柱段和锥段的相交截面作速度场与压力场分布对比曲线,对溢流口直径对水力旋流器内部流动情况及分离性能的影响进行分析。
3.3.1 溢流口直径对速度分布的影响
图5为不同溢流口直径下水力旋流器的速度分布对比图。 由图5可以看出,切向速度的值从壁面到轴心先逐渐增大到一极大值后再迅速减小。溢流口直径大小变化时,从水力旋流器壁面到距中心轴约0.03 m位置之间的流体流速极为接近,说明在此区域内流体流速基本不受溢流口直径影响,但在0.03 m以内的区域,溢流口直径增大时切向速度与轴向速度明显减小。

图5 溢流口直径对速度分布的影响
3.3.2 溢流口直径对压力分布与压降的影响
图6表示了溢流口直径变化对水力旋流器静压力分布的影响。 可以看出随着溢流口直径的增大,旋流器内静压力显著降低,轴心附近的负压小幅度升高。 此外,轴心附近水平方向上负压范围随溢流管直径的增加而增大。
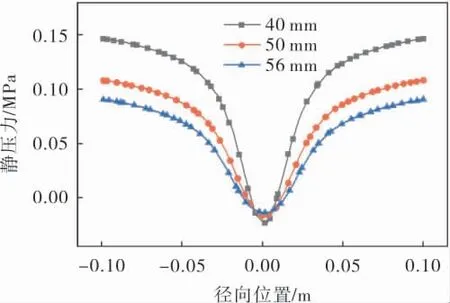
图6 溢流口直径对压力场的影响
图7为不同溢流口直径对应的水力旋流器压降, 可以看出水力旋流器压降随溢流口直径的增大而显著下降。 这是因为溢流口直径增加时旋流器内流体切向与轴向流速降低,流动能耗也降低。
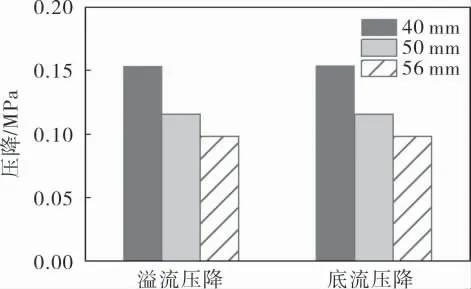
图7 溢流口直径对压降的影响
3.3.3 溢流口直径对分离效率的影响
溢流口直径对颗粒分离效率的影响如图8所示,可以看出,在给定入口流速下,水力旋流器对颗粒的分离效率会随溢流口直径的增大而减小,且减小趋势在粒径30 μm以下的颗粒上表现的更加显著。 主要原因是切向速度的大小决定着离心力的大小, 溢流口直径增大时轴心附近流体的切向速度减小,颗粒受到的离心力降低,所以分离效率也减小。 其次,溢流口直径变大,就会使更多的流体从溢流口排出, 自然会有更多颗粒由溢流口离开旋流器,从底流口排出的颗粒占比降低。

图8 溢流口直径对分离效率的影响
由以上分析可以看出,溢流口直径增加后水力旋流器的压降明显降低,而溢流口直径增大虽然会降低颗粒分离效率, 但仅对粒径在30 μm以下的颗粒有较明显影响。 因此最终选择溢流口直径为56 mm, 此时水力旋流器可以在保持整体分离效率较高的条件下有较低的能耗。
3.4 入口流速对水力旋流器性能的影响
入口流速决定了水力旋流器内离心强度与处理量大小。 分别在入口流速为5、7、9、11 m/s的条件下进行CFD数值模拟, 并对比分析流速对水力旋流器性能的具体影响,速度与压力分布均在圆柱段与锥段的交界截面取值。
3.4.1 入口流速对速度分布的影响
图9所示为不同入口流速对应的水力旋流器切向与轴向速度分布曲线。 可以看出,随着入口流速的上升, 切向与轴向速度增幅与降幅均增大。观察图8b可以发现在入口流速为11 m/s时,轴向速度在几个位置出现了强烈波动,表现出了不稳定性, 说明当入口流速大于等于11 m/s时水力旋流器难以维持稳定的运行。

图9 入口流速对速度分布的影响
3.4.2 入口流速对压力分布与压降的影响
图10为旋流器内压力场随入口流速的变化对比曲线,可以看出随着入口流速的增加,水力旋流器靠近壁面附近的压力大幅升高,轴心附近的压力略微降低。
不同入口流速下对应的水力旋流器压降如图11所示,可以看出水力旋流器压降会随流速的增大而大幅上升。 这是因为流速增加后,同一时间内通过旋流器的流体流量增大,更大量的流体在旋流器更高速的运行,消耗了更多能量,压降就大幅提高。

图11 入口流速对压降的影响
3.4.3 入口流速对分离效率的影响
入口流速从5 m/s增大到11 m/s时,水力旋流器对不同粒径的颗粒分离效率的影响不同,如图12所示。粒径为10 μm时,颗粒分离效率随流速的增大反而减小;粒径在20 μm时,流速由5 m/s增大到7 m/s时颗粒分离效率增大,流速再继续增大分离效率就开始减小;粒径在30 μm时,流速由5 m/s增大到9 m/s时颗粒分离效率持续增大,增大至11 m/s后分离效率减小; 粒径在40 μm以上时,颗粒的分离效率随流速增大而增大。 出现以上现象的主要原因是流速增大会使离心力增大,有助于颗粒被离心至壁面,分离效率提高。 但流速过大会缩短流体在水力旋流器内的停留时间,导致小颗粒还未来得及被离心至外侧就已经随内旋流从溢流口流出,就出现分离效率随流速增大而减小的现象。 对于40 μm及以上的大颗粒来说,大流速对应的流体停留时间已经足够其被离心分离,所以分离效率只会因流速增大导致的离心力增大而增大。 可以合理推测,流速不断增加的过程中,任意粒径大小的颗粒的分离效率总是呈现先增大后减小的趋势。

图12 入口流速对分离效率的影响
入口流速越大,水力旋流器单位时间的处理量越大。 所以应在不致使颗粒总体分离效率下降的前提下尽量选择大流速以同时提高处理量与分离效率。由以上分析可知,流速为11 m/s时粒径在40 μm以下颗粒的分离效率均出现明显的下降,所以最适宜的流速应为9 m/s。
3.5 锥角对水力旋流器性能的影响
锥角会显著影响水力旋流器的性能。 常见的小锥角水力旋流器锥度一般在10~15°之间,分别选择锥角为10、12、15°,研究锥角变化对水力旋流器的流动特性和分离性能的影响,其中速度与压力分布的取值截面依然为柱锥段的交界面。
3.5.1 锥角对速度分布的影响
图13为锥角对水力旋流器速度分布的影响。可以看出,随着锥角从15°降为10°,水力旋流器的切向速度值小幅度减小,说明锥角对切向速度有较小的影响。 从图13b中可以看出,在轴心附近锥角减小轴向速度增大。
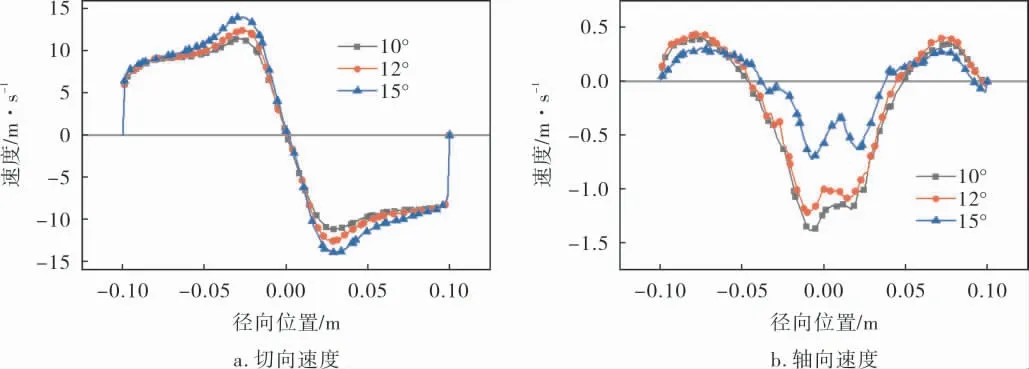
图13 锥角对速度分布的影响
3.5.2 锥角对压力分布与压降的影响
锥角变化对水力旋流压力分布的影响如图14所示,锥角由15°变化到10°的过程中,水力旋流器壁面附近的压力明显减小。
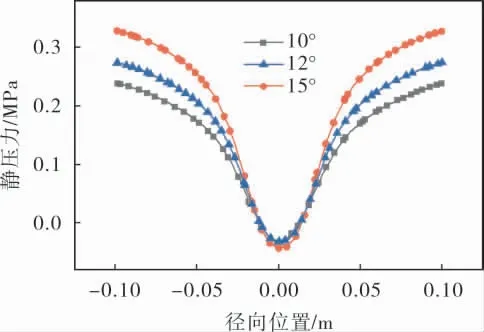
图14 锥角对压力场的影响
图15为锥角分别为10、12、15°时水力旋流器的压降。 可以看出水力旋流器压降随着锥角的减小而下降,结合图13可以得出结论,锥角减小降低了流体的总体流速,使流动过程中的能量损失降低,说明减小锥角有助于降低水力旋流器的能耗。

图15 锥角对压降的影响
3.5.3 锥角对分离效率的影响
锥角对水力旋流器分离效率的影响如图16所示,锥角由15°减小为10°后,粒径在10~30 μm范围内的颗粒分离效率明显增大, 粒径在10 μm附近的颗粒分离效率提高约15%。 这是因为减小锥角会使水力旋流器的锥段增长,这使流体有了更长的停留时间,颗粒就有了充足的时间在离心力的作用下运动到外旋流并从底流口排出。
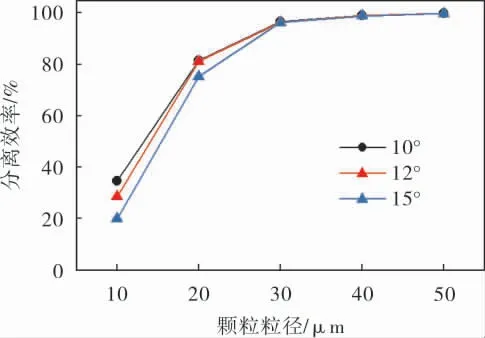
图16 锥角对分离效率的影响
锥角为10°时,旋流器对粒径在20 μm以上的颗粒的分离效率可达80%以上, 达到了较好的分离效果,并且此时水力旋流器压降较低,仅有0.26 MPa,所以10°为所选水力旋流器最佳锥角。
3.6 高海拔对水力旋流器性能的影响
前文为高海拔条件下的模拟结果,将优化后的水力旋流器在平原条件下的工作状况进行CFD模拟,并与前文结果进行对比,研究海拔改变对水力旋流器运行过程是否有影响。
3.6.1 高海拔对速度分布的影响
图17为水力旋流器在大气压强72.4 kPa的高海拔地区与大气压强101.325 kPa的平原地区的速度分布差异。 可以看出海拔变化对切向速度基本无影响, 只对轴心位置的轴向速度有微弱影响,海拔升高后,轴心附近的轴向速度绝对值有极小幅度的增大。 原因是重力加速度是向下运动的加速度、向上运动的减速度,轴心附近为向上运动的内旋流,表现出了随重力加速度的小幅度减小而略微增大的现象。
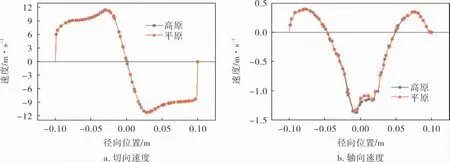
图17 高海拔对速度分布的影响
3.6.2 高海拔对压力分布与压降的影响
图18是水力旋流器内静压力分布在平原和高原的对比图。 可以看出,静压力分布基本不随海拔的变化而改变。

图18 高海拔对压力场的影响
图19为水力旋流器在平原和高原的压降值。可以看出,平原地区与高原地区压降基本相同。
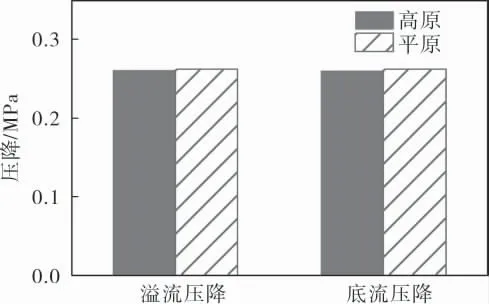
图19 高海拔对压降的影响
3.6.3 高海拔对分离效率的影响
由海拔变化前后水力旋流器的分离效率对比图(图20)可以看出,海拔变化对颗粒分离效率影响极小, 只在粒径大小在30 μm附近时高原的分离效率相较平原有极小幅度的增大,原因可能是重力加速度的减小减弱了流体在水力旋流器内部的轴向运动,让混合流在旋流器内部的停留时间有小幅度的增加,分离效率就有了微小的增大,但由于重力加速度的变化幅度很小,所以分离效率的变化不明显。
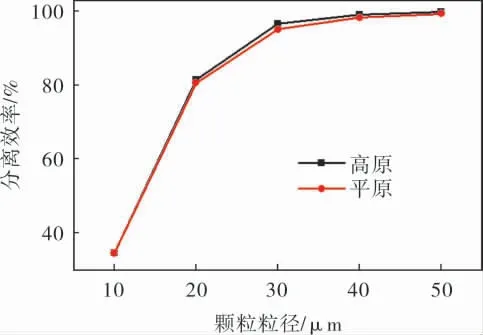
图20 高海拔对分离效率的影响
综合以上分析,海拔高度变化对水力旋流器的固液分离过程影响非常微小,在水力旋流器选型时不必顾虑海拔高低对其流动过程及分离性能的影响。
4 结论
对于在青海盐湖的钾肥生产过程中产生的KCl冷结晶器溢流液, 提出了使用水力旋流技术进行固液分离的方法, 采用CFD方法研究了溢流口直径、入口流速、锥角和海拔等因素对水力旋流器性能的综合影响,并特地将青海盐湖的高原地理条件作为初始条件考虑,得出了以下结论:
a.增大溢流口直径会使水力旋流器的分离效率与压降明显降低;
b.增加入口流速会使颗粒的分离效率先上升后下降,使水力旋流器的能耗单调上升;
c.锥角减小有助于提升水力旋流器的分离效率,还可以降低水力旋流器的压降;
d.海拔高度变化对水力旋流器的固液分离过程影响极小;
e.模拟计算后得出的最佳结构参数与操作参数分别为Dc=200 mm、d0=56 mm、锥角α=10°、入口流速为9 m/s,在此条件下水力旋流器可以在较大处理量及低能耗下对20 μm以上颗粒达到80%以上的分离效率,此时压降为0.26 MPa。
