近场动力学最小二乘和有限元耦合方法研究

郑庆胜, 张树翠*, 孙可明 李 凯, 张欣刚

(1.青岛理工大学 理学院,青岛 266520; 2.青岛市地下非常规能源开发工程研究中心,青岛 266520)

1 引言

材料和结构的损伤及破坏涉及连续到不连续变形的过程,是计算固体力学领域长期存在的难题之一。以传统连续介质力学为基础的数值模型和方法在求解固体材料和结构渐进破坏全过程尤其是复杂不连续问题(如多裂纹扩展和分叉等)时存在困难[1-3]。近场动力学PD(peridynamic)是由Silling等[4,5]提出的非局部连续理论,该理论采用积分方程取代微分方程,允许位移场出现间断,能够在统一的框架下求解连续和非连续问题。目前主要有键基、常规态基和非常规态基近场动力学三种PD模型。键基PD存在固定泊松比的限制,常规态基PD虽然没有泊松比的限制但不包括应力应变的概念,非常规态基PD的力密度向量由应力和应变向量表示,并可以应用传统的本构模型,但存在零能模式[6]。随后,Madenci等[7]基于PD理论发展出了近场动力学微分算子,建立起了微分方程和积分方程之间的桥梁。作为推导近场动力学微分算子的替代方法,近场动力学最小二乘[8]基于最小二乘法和Taylor级数展开推导近场动力学微分算子,而不需要在每个点构造近场动力学函数。

相比于有限元法,PD的计算效率较慢,且在施加边界条件方面存在困难。为了结合PD在处理裂纹扩展问题和FEM计算效率高、便于施加边界条件的优势,许多学者进行了FEM和PD耦合的研究。Liu等[9]提出将FEM区域和PD区域通过界面单元耦合在一起,但需要在界面单元内嵌入PD结点计算耦合力并将其映射到有限元结点。Lubineau等[10]采用解析的方法,提出了一个包含局部和非局部连续的统一模型,通过采用渐变函数实现局部和非局部模型在混合区域的平滑过渡。章青等[11]提出了通过力耦合的近场动力学与有限元混合建模的隐式分析方法,该方法不需要设置重叠区域,交界面上的有限元结点除了与该单元的其他有限元结点发生作用,还通过杆单元与半径为r范围内的其他物质点发生作用。Zaccariotto等[12]提出了一种简单有效的FEM单元和PD网格耦合方法,并且不需要设置耦合区域。Liu等[13]扩展了Zaccariotto等[12]的方法,将其应用于非常规态基PD与FEM耦合。Liu等[14]提出了耦合近场动力学最小二乘和FEM的方法,并用于模拟准静态裂纹扩展,但需要在每个PD结点引入映射矩阵。

本文在文献[12,13]的研究基础上,将该方法应用于近场动力学最小二乘和有限元耦合。该方法的优势在于不需设置重叠区域,不必在界面单元内嵌入PD结点,也不用引入额外的映射矩阵,数值实现简便直接,稍加改造即可扩展到已有的有限元程序中,不含零能模式,并且包含了应力和应变的概念。

2 近场动力学最小二乘与有限元耦合方法

2.1 近场动力学最小二乘

在二维空间中,基于近场动力学相互作用的概念、最小二乘法和Taylor级数展开,由物质点x与其近场范围Hx内的其他物质点x′的相互作用,其中Hx由近场范围尺寸δ确定,如图1所示,得到上至二阶导数的近场动力学积分形式的表达式[8]

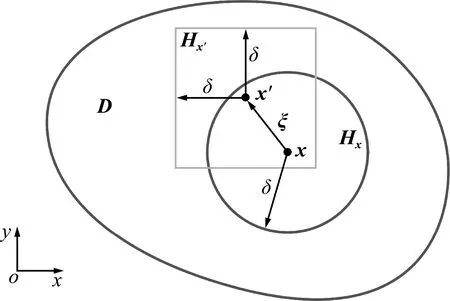
图1 物质点的相互作用域(族)Fig.1 Interaction domain (family) of material points

(1)

式中ω(|ξ|)为反映物质点间相互作用程度的权函数,可以根据导数向量阶数的不同而不同。A为形状矩阵,具体表达式参考文献[8]。r为空间变量向量,可以表示为

(2)

式中ξ=x′-x,x′∈Hx。

式(1)中等号右侧前三项ω(|ξ|)A-1r对应于近场动力学微分算子中的近场动力学函数[7],即

(3)

传统连续介质力学中的运动方程为

(4)

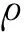
σ(x,t)=λtr(u)I[u+(u)T]

(5)

·σ(x,t)2u(x,t)+(λ)·u(x,t)

(6)

基于近场动力学积分形式的导数表达式,可以将式(5,6)写为积分形式

μ(u′-u)⊗d+μd⊗(u′-u)dVx′]

(7)

和

(8)

式中u(x′)和u(x)分别简记为u′和u,向量d和矩阵D定义为

(9)

2.2 刚度矩阵和质量矩阵耦合

为了将近场动力学最小二乘和FEM进行耦合,首先将裂纹区域和裂纹可能扩展区域划分为PD区域,其他区域划分为FEM区域。对求解区域进行统一离散,在PD区域的结点称为PD结点,在FEM区域的结点则称为FEM结点,PD结点会与其族范围内的其他结点产生相互作用,而FEM结点仅会与该单元中的结点产生相互作用。PD和FEM的界面区域的单元称为混合单元,其特点是同一单元中同时含有PD结点和FEM结点。本文以一维情况为例对两者的耦合过程进行描述。

一维杆的离散和区域划分情况如图2所示,PD结点的近场范围δ取为2l。

图2 一维杆的耦合模型Fig.2 1D coupled model of a bar

(10)

式中A和l分别为杆单元的横截面积和长度,a=EA/l。

(11)

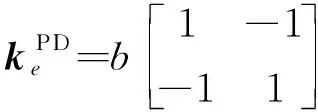
(12)

式中b=(2E/Aδ2l)VxVx′。

(13)

以上三种单元的单元刚度矩阵组装得到整体刚度矩阵。对于图2所示的一维模型,整体刚度矩阵K不是对角阵,也不是对称阵。其第4行和第5行的元素为

(14)

由式(14)可知,通过该方法得到的整体刚度矩阵中,每一行的非零元素个数是包含自身结点在内的相互作用的结点数目,如图2中5号结点与3号、4号、6号和7号结点产生相互作用,则第五行中这些结点编号对应位置为非零元素。

质量矩阵的耦合方法与刚度矩阵的耦合方法类似。该方法可以与一致质量矩阵和集中质量矩阵进行耦合,本文FEM区域的质量矩阵采用一致质量矩阵。

(15)

(16)

(17)

与刚度矩阵类似,用该方法得到的整体质量矩阵也是非对称矩阵。对于图2所示的一维模型,整体质量矩阵M可写为三对角阵,其主对角元素为

diag(M)=[2c,4c,4c,4c,d,d,…]

(18)

上对角元素前四个为c,其余为零。下对角元素为前三个为c,其余为零。

该耦合方法的整体刚度矩阵和整体质量矩阵的计算过程如下。

(1) 根据求解区域的PD和FEM的区域划分情况,得到FEM单元和混合单元以及FEM结点和PD结点的信息。

(2) 先计算所有FEM单元和混合单元的单元刚度矩阵和单元质量矩阵,并组装到整体刚度矩阵和整体质量矩阵。在此计算中将混合单元视为FEM单元。

(3) 整体刚度矩阵和整体质量矩阵的修正,将步骤(2)得到的整体刚度矩阵和整体质量矩阵中PD结点对应行的数值设置为零。

(4) 对所有的PD结点进行循环,计算当前PD结点与其族内所有结点相互作用的单元刚度矩阵并组装到整体刚度矩阵中,并最终得到该耦合方法的整体刚度矩阵和整体质量矩阵。

2.3 断裂准则

PD中应用比较广泛的断裂准则为临界伸长率准则,当物质点之间键的伸长率超过临界值时,键就会断裂,物质点之间的相互作用消除。物质点之间键的伸长率定义为[1,15]

s=(|ξ+η|-|ξ|)/|ξ|

(19)

(20)

式中sc为临界键伸长率,根据文献[15],两个物质点之间的微模量为

(21)

式中C(ξ)表示为

(22)

对于足够大的均质体的各向同性膨胀,每个键的伸长率s都相同,则有η=sξ,式(22)可以写为

(23)

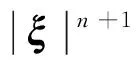
(24)

对于平面应力问题ν=1/3和平面应变问题ν=1/4,式(24)可以恢复为键基近场动力学的临界伸长率表达式。

一点处的局部损伤定义为[1,15]

(25)

2.4 求解方法

利用得到的整体刚度矩阵和整体质量矩阵,最终得到整体动力学方程

(26)

式中M和K分别为整体质量矩阵和整体刚度矩阵,F和δ分别为载荷向量和位移向量。

对于静态问题,不考虑加速度,式(26)可以写为

Kδ=F

(27)

采用Newmark方法[16]对动态问题进行求解,本文参数选择为γ=0.5,β=0.25。对于静态问题则进行直接求解。

3 数值算例

为了验证本文耦合方法的有效性和准确性,对一维和二维的静态和动态问题进行研究。

3.1 一维问题

3.1.1 静态问题

两种数值方法之间的耦合可能会在计算模型中产生ghost forces[10,13]。对该耦合方法的ghost forces进行测试需要给出正则化的绝对和相对误差,定义如下

(28)

一维杆的几何和区域划分如图3所示,杆长L=1 m,横截面积A=4×10-4m2,弹性模量E=200 GPa,杆的左端固定,右端承受集中力F=10 kN。求解区域离散成20个单元,含有10个FEM结点和11个PD结点,单元长度Δx=50 mm,每个PD结点的近场范围δ=3Δx。

图3 一维杆的几何、区域划分和边界条件Fig.3 Geometry,region division and boundary conditions of 1D bar

该问题的解析解为

u(x)=F/(AE)x=1.25×10-4x

(29)

式(28)得到该模型的绝对和相对误差分别为1.0007×10-18和1.3431×10-14。数值解与解析解的结果对比如图4所示。可以看出,数值解与解析解吻合非常好,并且不受ghost forces问题的影响。

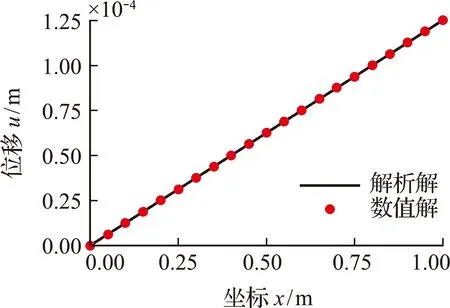
图4 杆的轴向位移Fig.4 Axial displacements along the bar

3.1.2 动态问题

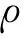
u(x,0)=εx,ε=0.001

(30)

初始速度为零。该问题的解析解为[17]

(31)

求解区域划分为1000个单元,含有500个FEM结点和501个PD结点,单元长度Δx=1 mm,每个PD结点的近场范围δ=3Δx。时间步长Δt=1×10-6s,结束时间t=0.005 s。

杆的中点(x=0.5L)和右端点(x=L)的位移-时间曲线如图5所示。数值解与解析解吻合非常好,成功捕捉到了杆的轴向振动。

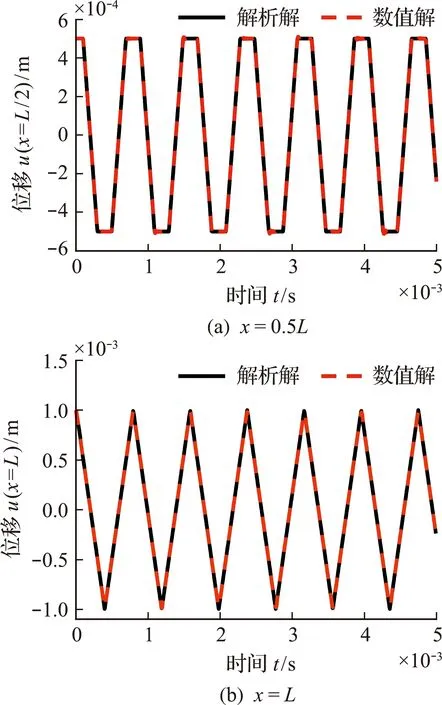
图5 位移-时间曲线Fig.5 Displacement variation with time

3.2 二维问题

3.2.1 静态问题

如图6所示,板左端固定,右端载荷P=10 MPa,板的边长L=W=1 m,厚度h=1 mm,弹性模量E=72 GPa,泊松比ν=0.22。 区域划分如图6所示,将其离散成40401个单元,单元长度Δx=5 mm,每个PD结点的近场范围δ=3Δx。

图6 板的几何和边界条件Fig.6 Geometry and boundary conditions of the plate

沿板中轴线的应力曲线与FEM的对比结果如图7所示。两者结果一致性较好。

图7 沿中轴线的应力对比Fig.7 Stress comparison along the central axis

3.2.2 动态问题

图8 含有预制裂纹的板Fig.8 A plate with a pre-existing crack

该耦合方法裂纹的扩展结果与文献[19]对比如图9所示。首先,裂纹沿水平方向扩展,在扩展了约15 mm后,裂纹开始分叉。该耦合方法成功捕捉到了裂纹的分叉行为,与文献[19]裂纹扩展路径吻合较好。

(注:(a～c)由本文耦合方法得到)图9 裂纹扩展路径Fig.9 Crack propagation path

4 结 论

本文对近场动力学最小二乘和有限元耦合方法进行了研究。该耦合方法数值实现简单直接,结合了近场动力学最小二乘处理非连续问题和有限元处理连续问题的优势,没有零能模式,并且包含了应力和应变的概念。边界区域设置为FEM区域,方便边界条件的施加,裂纹及其可能扩展区域设置为PD区域,用于裂纹扩展的模拟。通过对一维和二维的静态和动态问题研究验证了该耦合方法的有效性和准确性。基于近场动力学最小二乘在微分方程和积分方程之间的桥梁作用,该耦合方法也可以用于其他问题的求解,如耦合场问题等。