各向异性对平板裂纹扩展路径的影响研究

张向奎, 申国哲, 许 博, 郑国君, 胡 平, 李伟东*

(1.大连理工大学 人工智能学院,大连 116024;2.大连理工大学 汽车工程学院,大连 116024)

1 引言

断裂路径的数值模拟是一个持续存在且亟需解决的力学难题。经典连续介质力学并不适合用来求解断裂不连续问题,其原因在于不连续情况下应力张量空间导数会出现奇异性。传统有限元方法以经典连续介质力学理论为基础,在处理不连续问题时需要重新划分网格或者借助附加的失效准则才能进行求解,而且需要预先知道裂纹存在的位置,无法进行准确的裂纹路径预测。为改进传统有限元方法的不足,提出内聚力单元和扩展有限元法用于裂纹扩展路径分析。然而,内聚力单元同样需要预先得知裂纹的扩展路径,而且具有较强的网格依赖性;扩展有限元法需要引入复杂的断裂准则,无法应用于多裂纹扩展的情况。

Silling[1]提出的近场动力学PD(Peridynamics)理论是一种非局部作用理论,不仅满足连续介质力学理论中所有的基本平衡定律,而且由于其运动方程采用空间积分形式代替经典连续介质力学理论中的偏微分方程,因此在无需额外断裂准则的情况下也能够模拟裂纹的萌生、扩展和多裂纹分支等过程[2]。在近场动力学理论中,认为一个物体是由许多物质点构成的,每个物质点都通过键与邻域内的其他物质点相连,考虑两个物质点之间的键力而摒弃了经典连续介质力学理论中的应力和应变概念。目前,近场动力学理论发展迅速,广泛用于各种材料的断裂问题。

绝大部分工程材料都是各向异性的,由于其强度和刚度跟材料方向相关,因此裂纹扩展路径也要比各向同性材料更为复杂。Kilic等[3]采用键基近场动力学理论预测了带有中心裂纹的复合材料层合板的渐进损伤过程。Hu等[4]针对单向纤维增强复合材料提出了一种键基近场动力学计算模型,可用来分析任意纤维方向的纤维增强复合材料的损伤行为。Oterkus等[5]应用键基近场动力学理论实现了机械载荷和热载荷作用下的纤维增强复合材料损伤过程的分析。Ghajari等[6]提出了一种基于键基近场动力学理论的二维正交各向异性材料模型,用于预测复杂各向异性材料的动态裂纹扩展问题。Hu等[7]通过引入面内法向、面内剪切、横向法向和横向剪切键,提出了一种新的正交各向异性键基近场动力学模型。但这些近场动力学模型的材料参数均受到一定限制。

为了解除材料参数的限制,学者们又提出了各种扩展键基近场动力学模型。Diana等[8]在微极近场动力学框架下提出了一种原始的正交各向异性面内线弹性模型,获得了以四个独立参数为特征的正交各向异性平面键基模型,该模型可用于分析受到均匀和不均匀变形的各种二维柯西正交各向异性材料的力学行为。陈瑞[9]提出了一种改进的正交各向异性单向板键基近场动力学模型,考虑了物质点旋转和剪切变形,能够用来分析正交各向异性单向板在准静态载荷作用下的变形和动态载荷作用下的裂纹扩展问题。Zhang等[10]提出了一种新的二维常规态基正交各向异性近场动力学模型,引入了四个材料参数,定义了三种临界拉伸,能够应用于二维正交各向异性材料的弹性和断裂分析。Hattori等[11]提出了一种可用于模拟各向异性材料的非常规态基近场动力学公式,可用于分析二维各向异性材料的裂纹扩展行为,但是非常规态基具有固有的零能模式和数值不稳定性,容易导致错误的结果。Tian等[12]提出了一种新的各向异性公式,可用于分析二维正交各向异性薄板的弹性、损伤和断裂行为,但是该模型只定义了三个独立的弹性常数,另一个材料参数需要预先设定。

基于近场动力学理论进行一般各向异性材料的裂纹扩展路径研究,目前尚未进行。本文首先以微梁键[13-15]为基础,通过类比经典连续介质力学理论中弹性矩阵的变换关系,提出了微模量的一般各向异性表达式,从而使微梁键具有各向异性;接着,通过插值建立了一般各向异性平面模型的近场动力学应变能密度,并基于应变能密度互等原理求出一般各向异性近场动力学本构模型参数;最后,通过实际案例分析了各向异性对平板裂纹扩展路径的影响。

2 一般各向异性近场动力学板模型

2.1 各向异性微梁键

在边长为2δ的正方形板单元上有一个由点xi和其相邻点xj组成的微梁键ij,如图1所示。图1共有三个坐标系,即材料坐标系12、板单元的局部坐标系XYZ和微梁键的局部坐标系xyz。β为微梁键坐标系x轴与板单元坐标系X轴的夹角,ϑ为微梁键坐标系x轴与材料坐标系1轴的夹角,ζ为材料坐标系1轴与板单元坐标系X轴的夹角。

图1 微梁键及坐标系Fig.1 Micro-beam bond and coordinate systems

为使微梁键具有各向异性,PD微梁键的微模量应该随着角度的变化而连续变化,本文采用类比经典连续介质力学理论中两个坐标系之间弹性矩阵的变换关系来表示各向异性微梁键的两个微模量。在经典连续介质力学理论中,微梁键坐标系和材料坐标系之间弹性矩阵的变换关系可表示为

(1)

式中

(2)

由式(1)得

Qxx=Q11cos4ϑ+2Q12sin2ϑcos2ϑ+

4Q16sinϑcos3ϑ+Q22sin4ϑ+

4Q26sin3ϑcosϑ+4Q66sin2ϑcos2ϑ

(3)

Qss=Q11sin2ϑcos2ϑ-2Q12sin2ϑcos2ϑ-

2Q16(cos2ϑ-sin2ϑ)sinϑcosϑ+

Q22sin2ϑcos2ϑ+Q66(cos2ϑ-sin2ϑ)2+

2Q26(cos2ϑ-sin2ϑ)sinϑcosϑ

(4)

式中Qxx为轴向刚度,Qss为剪切刚度。因此,可定义微梁键的微模量为

4c16sinϑcos3ϑ+c22sin4ϑ+

4c26sin3ϑcosϑ+4c66sin2ϑcos2ϑ

2c16(cos2ϑ-sin2ϑ)sinϑcosϑ+

c22sin2ϑcos2ϑ+c66(cos2ϑ-sin2ϑ)2+

2c26(cos2ϑ-sin2ϑ)sinϑcosϑ

(5)

2.2 各向异性PD板应变能密度

微梁键对点xi贡献的面内微势能可以表示为

(6)

(7)

kij=ξ-3×

(8)

式中kij为微梁键刚度矩阵,uij为面内位移矢量。点xi的应变能密度可写为

(9)

定义图1的正方形板单元中4个节点的位移向量为

(I=1,2,3,4)

(10)

板单元面内任意一点的位移向量U={UVΘZ}T可通过插值得

U=N(p,q)Ue

(11)

插值函数N(p,q)由文献[13]给出。在单元局部坐标系下,微梁键端点的位移矢量可表示为

(12)

结合式(11,12),可得

Uij=Ue,

(13)

因此,在微梁键局部坐标系下的微梁键端点位移向量可写为

uij=TUij=TUe

(14)

式中β为微梁键坐标系x轴与板单元坐标系X轴的夹角。最终,可得板单元上任意一点的应变能密度为

(15)

2.3 各向异性PD板本构参数求解

考虑板的法向旋转角度,基于最小势能原理的变分方程可表示为

(16)

式中

(17)

因此,板内任意一点处的应变能密度可写为

(18)

让应变能密度相等,联立式(15,18),可求得微梁键的本构参数为

(19)

2.4 退化至各向同性PD板模型

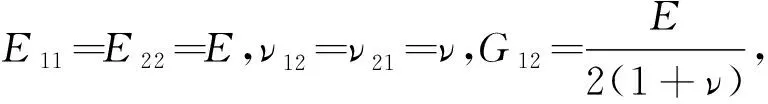
(20)

将式(20)代入式(5)可得

(21)

3 断裂准则

临界微势能可以表示为

wu(β,ζ)=wu2+(wu1-wu2)cos6(β-ζ)

(22)

式中β为微梁键坐标系x轴与板单元坐标系X轴的夹角,ζ为材料坐标系1轴与板单元坐标系X轴的夹角。随着夹角ζ的变化而变化,考虑ζ=0和ζ=π/2时材料的断裂能等于断裂面上断裂所有的键所做的总功,可得

cos6β}t|ξ|dβdξdz

cos6(β-π/2)}t|ξ|dβdξdz

(23)

化简可得

(24)

ζ=0和ζ=π/2时材料的断裂能可以定义为

(25)

4 各向异性对裂纹路径的影响

本文以带预制切口的平板受面内拉伸载荷时的裂纹扩展为例,重点研究各向异性参数对平板裂纹扩展路径的影响规律。

用于裂纹扩展路径研究的预制切口平板尺寸及边界情况如图2所示。平板采用均匀四边形单元离散,单元平均尺寸为1.0 mm,近场域大小取单元尺寸的3倍,时间步长取Δt=1×10-8s,加载于平板上下边缘的载荷在整个模拟过程中保持恒定不变。

图2 预制切口平板的尺寸及边界情况Fig.2 Dimensions and boundary conditions of a pre-notched rectangular plate

平板为各向同性材料时,裂纹扩展路径的仿真结果与实验结果对比如图3所示,其中平板弹性模量为E=72 GPa,材料密度为ρ=2440 kg/m3,泊松比为ν=1/3,断裂能释放率为Gc=135 J/m2。结果表明,仿真结果与实验结果具有良好的对应性。

图3 各向同性预制切口板的裂纹扩展路径对比Fig.3 Crack propagation path of the isotropic pre-notched plate

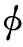
4.1 r对裂纹扩展路径的影响

为了研究r对裂纹扩展路径的影响,保持E1=72 GPa及其他材料参数和边界条件均不变,不同r值下预制裂纹板的最终裂纹扩展路径如图4～图7所示。

图4 E2=70 GPa, r=1.0286时预制切口板的裂纹扩展路径Fig.4 Crack propagation path of the pre-notched plate with E2=70 GPa and the r=1.0286

图6 E2=65 GPa, r=1.1077时预制切口板的裂纹扩展路径Fig.6 Crack propagation path of the pre-notched plate with E2=65 GPa and the r=1.1077

图7 E2=55 GPa, r=1.3090时预制切口板的裂纹扩展路径Fig.7 Crack propagation path of the pre-notched plate with E2=55 GPa and the r=1.3090

结果表明,随着E2的不断减小,各向异性不断增强时,裂纹扩展路径的分叉角度越来越小,当各向异性超过一定阈值时,分叉角度趋于0,此时裂纹扩展路径沿着弹性模量较大值的方向进行。

4.2 ζ对裂纹扩展路径的影响

取E1=72 GPa,E2=68 GPa及其他材料参数不变,材料坐标系1轴与板单元坐标系X轴的夹角ζ不断变化时,预制裂纹板的最终裂纹扩展路径如图8～图11所示。

图8 ζ=30°时预制切口板的裂纹扩展路径Fig.8 Crack propagation path of the pre-notched plate with ζ=30°

图9 ζ=45°时预制切口板的裂纹扩展路径Fig.9 Crack propagation path of the pre-notched plate with ζ=45°

图10 ζ=60°时预制切口板的裂纹扩展路径Fig.10 Crack propagation path of the pre-notched plate with ζ=60°

图11 ζ=90°时预制切口板的裂纹扩展路径Fig.11 Crack propagation path of the pre-notched plate with ζ=90°

结果表明,随着ζ的不断变化,裂纹扩展路径随之发生偏转,但是当ζ正好偏转90°时,虽然分叉角度略有增大(图11与图5相比),但是裂纹扩展路径又恢复为上下对称形式。

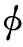
图12 =85°时预制切口板的裂纹扩展路径Fig.12 Crack propagation path of the pre-notched plate with =85°

图13 =75°时预制切口板的裂纹扩展路径Fig.13 Crack propagation path of the pre-notched plate with =75°

图14 =60°时预制切口板的裂纹扩展路径Fig.14 Crack propagation path of the pre-notched plate with =60°

图15 =40°时预制切口板的裂纹扩展路径Fig.15 Crack propagation path of the pre-notched plate with =40°

5 结 论

(1) 基于微梁键理论的一般各向异性近场动力学平板模型,由于没有任何材料参数上的限制,可以很好地模拟各向异性材料的动态断裂问题。

(2) 主轴各向异性差异性越大,其裂纹分叉性能越低,材料更趋向于沿着主轴方向断裂。

(3) 对于各向异性材料来说,材料主轴方向及主轴间夹角对结构的裂纹扩展路径方向具有不可忽略的作用。