基于Python-Abaqus的自适应网格重划分算法实现及其应用

徐亚飞, 肖映雄, 吴宇航

(湘潭大学 土木工程与力学学院,湘潭 411105)

1 引言

在有限元计算中,影响其结果准确程度的因素很多,如单元类型的选取和网格的疏密等。对于给定的实际问题,当选取了合适单元类型后,则需根据问题特点和计算精度设置网格的疏密。如对应力集中问题,需要采用自适应网格才能获得满足给定精度的数值解。自适应网格技术,包括自适应加密或自适应网格重划,相应的自适应有限元方法可减轻计算精度与计算量的矛盾[1-5]。目前,在自适应有限元方面也取得了大量的研究成果,如文献[6,7]为膜结构极小曲面找形和自由振动问题提出了相应的自适应有限元方法;文献[8,9]设计了基于局部误差控制标准的p型自适应有限元法,并应用于混凝土骨料模型的数值模拟;文献[10]提出了一种基于自适应网格加密和人工神经网络的有限元降阶模型;文献[11]提出了变截面变曲率梁振型的有限元后处理超收敛拼片恢复方法,获得了相应的网格自适应分析方法。各类新型自适应方法为解决实际工程问题提供了高效计算方案。

一般而言,可在Abaqus软件平台上通过GUI操作进行有限元计算与模拟,但当需要多次和反复进行时,或者需要重复改动某些参数和改动原来在GUI中不能改动的参数时,迫切需要利用Python对Abaqus进行二次开发。利用Python语言可以利用Abaqus脚本接口绕过Abaqus/CAE的图形用户界面GUI,直接对Abaqus内核进行操作。目前,在Abaqus二次开发及应用方面,已有很多研究成果[12-17]。二次开发技术还运用到了其他相关的领域中,如研究裂纹的扩展[18],在金属切削仿真中防止网格的畸变[19]。基于Python编写的脚本可以Abaqus直接运行,可方便修改有限元模型和相关参数,提高建模效率和避免返工。

本文采用以前学者发展的网格重划分算法,利用Python-Abaqus进行有限元建模和模拟,从数值上分析了误差控制标准对计算结果的影响,实现了自适应求解全过程。所编Python脚本可绕过Abaqus/CAE的图形用户界面GUI,直接对Abaqus内核进行操作,从而实现从几何建模、网格剖分到自适应有限元求解的自动化处理。然后,将所编Python脚本应用于含有凹角或孔洞的非光滑物理区域、材料常数不连续和应力集中等几类典型问题的有限元分析中。结果表明,基于Abaqus网格重划技术的自适应方法对求解带奇性解的实际问题是非常有效的,通过迭代可获取最优网格,近似解可达到要求的求解精度。Python二次开发自适应计算与模拟,可方便多次修改模型和参数,实现全流程脚本控制,提高建模效率。

2 自适应网格重划算法及其实现

在实际应用中,由于无法事先决定网格的疏密分布,只能凭经验在梯度可能较大的部位进行网格加密/重划,使得网格加密/重划带有一定的盲目性。为了克服这种困难,需要采用自适应网格技术,其可将误差估计与有限元网格的生成和改正有机结合起来,力求用较少的单元获得预期的精度要求。对于一个特定的网格,在精确解未知的情况下,需要采用后验误差估计的方法来定量评价离散误差的大小,以便指示下一步的网格划分。在求得给定网格下有限元位移解和应力解后,采用应力恢复等方法构造出改正的应力解。研究表明,改正前的有限元应力解和改正后的应力解之差可用来估计有限元的误差。这种基于后验误差估计的自适应方法已广泛应用于各种实际问题的求解中,具有很好的普适性。

本节考虑基于后验误差估计的自适应网格重划算法,利用Python-Abaqus进行建模和模拟分析,实现自适应有限元求解全过程。

2.1 一般的自适应网格重划算法

自适应网格重划可以改善有限元计算结果的精度。一般如遇以下几种情形则需要采用自适应网格重划技术,(1) 事先不确定有限元网格需要怎样的细化来达到给定的计算精度要求; (2) 很难在感兴趣的区域(如应力集中)附近事先设计一个足够细化的网格; (3) 事先不知道网格需要细化的位置,如塑性区域的形成。下面给出自适应网格重划算法[1]的一般描述。

设Th是求解域Ω的任意四边形网格剖分,记单元数为Ne,其中,h为Th上所有剖分单元的最大尺寸。对给定的线性或非线性力学问题,假设在当前网格Th下,利用有限元法求解得到近似位移场{u}h、应变场{ε}h和应力场{σ}h。设原问题的精确位移场为{u},相应的应变场和应力场分别为{ε}和{σ}。定义误差{eu}={u}-{u}h,{eε}={ε}-{ε}h以及{eσ}={σ}-{σ}h。为了获取无量纲的相对误差度量,分别引入误差和精确解的能量范数,

(1)

(2)

(3)

(i=1,2,…,Ne)(4)

定义如下形式的单元误差指标,

(i=1,2,…,Ne)(5)

若ξi≤1对所有单元均成立,则当前网格已是最优,自适应计算结束;否则,按式(6)计算新的单元尺寸,

(对ξi>1)(6)

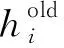
在实际应用中,应力精确解{σ}一般未知,可通过磨平技术得到改善后的近似解{σ*}代替{σ},进而计算误差范数。为保证{σ*}与相应的离散应力场{σ}h的预测值一致,需要满足

(7)

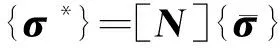
(8)

由此可得

(9)

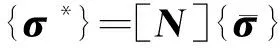
评注对于四边形等参元,由于Gauss积分点为超收敛点,其上的应力近似解比其他部位要具有更高的精度。在实际应用中,可以利用精度较高的Gauss积分点的应力值来改正节点应力值,再利用磨平技术(如绕节点加权平均),得到改善后的节点应力值{σ*}。

上述介绍的是计算应力近似解{σ*}的一种简单方法,精度更高的方法可采用文献[20]提出的应力恢复投影法(patch recovery technique of Z-Z method)或SPR方法[2]。

2.2 自适应有限元算法Python-Abaqus实现

Abaqus提供了自适应网格重划算法的GUI操作,但当需要多次、反复进行计算与模拟,且需要一些更高级的技巧来实现Abaqus中原来没有的一些功能或者需要重复改动某些参数,可以利用Python对Abaqus进行二次开发,编制相应的Python脚本,进而可直接在脚本中进行添加新功能或修改参数等,非常方便地实现自适应网格重划、完成有限元计算或模拟。

在Abaqus中,要实现自适应网格重划算法,需要选取下述三个重要指标。

(1) 误差指标变量。在分析中选取什么误差指标变量来实施自适应网格重划,需要考虑以下三个因素来进行选择, ① 误差指标的特征,② 分析模型场函数的类型, ③ 载荷的性质。

在Abaqus中,常用误差指标变量有单元能量密度(element energy density;ENDENERI)、密塞斯应力(Mises stress;MISESRI)、等效塑性应变(equivalent plastic strain;PEEQERI)、塑性应变(plastic strain;PEERI)、蠕变(creep strain;CEERI)、热流(Heat flux;HFLERI)和电势梯度等。本文主要选取单元能量密度和密塞斯应力作为误差指标变量。

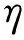
结合2.1节的一般自适应网格重划算法和Abaqus中给定的上述三个重要指标,可以得到自适应有限元算法流程,如图1所示。

图1 自适应有限元算法流程Fig.1 Flow chart of adaptive finite element algorithm

利用Python语言,自行编制了如图1所示自适应有限元算法的脚本文件。Python脚本实现网格重划与自适应计算的优点, (1) 可自行修改和重复性操作,且所需代码较少,如可灵活修改误差变量、重划网格的方法及误差目标等关键参数,非常方便; (2) 可实现各种循环操作以及数据存储等的自动化处理; (3) 可绕过Abaqus/CAE的GUI,直接对Abaqus内核进行操作,如可直接调用Abaqus的核心模块adaptivityProcesses()实现自适应网格重划及后续计算,避开了在不同对话框和标签页下输入数据等繁琐操作。

3 数值试验及结果分析

将所编Python脚本应用于含有凹角或孔洞的非光滑物理区域、材料常数不连续和应力集中等几类典型问题的有限元分析中,以考察全流程Python脚本的适应性和网格重划算法的有效性。

算例1(含圆孔的无限大薄板问题) 如图2所示,设长L=20 cm,宽W=10 cm,圆孔的圆心位于薄板的中心,半径R=1 cm,弹性模量E=2.1 GPa,泊松比ν=0.3,取单位厚度,均布荷载为q=10 kN/cm2。利用对称性,取模型的1/4作为研究对象,对应的有限元计算模型如图3所示。

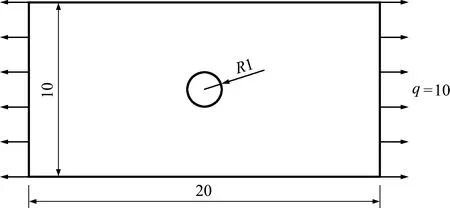
图2 带孔薄板Fig.2 Rectangular plate with a small hole

图3 有限元计算模型Fig.3 Finite element model

利用所编Python脚本进行分析,重点分析不同误差控制标准对计算结果的影响。自适应加密区域按不限定区域即自由划分,数值结果总结如下。

图4 圆孔上的应力数值解与精确解比较Fig.4 Comparisons for the numerical solutions and the exact solution of the stress on the circular hole

图5 当=1%时对应的初始网格和最终网格Fig.5 Initial mesh and the final mesh when =1%

图6 当=1%时对应的初始网格和最终网格Fig.6 Initial mesh and the final mesh when =1%

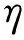
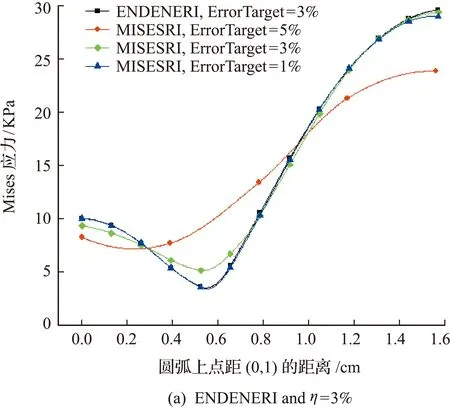
图7 两种不同误差控制标准下计算结果比较Fig.7 Comparisons of the computational results under two different error control standards

本文继续将所编Python脚本应用于含有凹角或孔洞的非光滑物理区域、材料常数不连续和应力集中等问题的有限元分析中,以进一步考察算法的有效性和Python脚本的适应性。

图8 开孔非规则薄板Fig.8 Irregular thin plate with holes

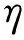
图9 当=1%时,自适应迭代初始网格和最终网格Fig.9 Initial mesh and the final mesh when =1%

图10 当=1%时,开孔非规则薄板应力云图Fig.10 Stress nephograms of irregular thin plate with openings when is equal to 1%

(双连拱隧道问题[22]) 考虑某双连拱隧道,其基本结构如图11所示。假设围岩及结构支护体系材料为均匀各向同性的线弹性材料,对应的材料参数列入表1。为较好地模拟隧道的受力情况,需要对外围边界条件进行近似处理,即左右边界取离隧道中心距离为60 m,上下边界取距离隧道中心距离为40 m。按平面应变问题分析隧道围岩和衬彻等在自重作用下的变形和应力分布。

图11 双连拱隧道结构Fig.11 Double arch tunnel structure

表1 材料参数Tab.1 Material parameters

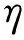
图12 初始网格和自适应迭代得到的最终网格重划Fig.12 Initial mesh and the final mesh obtained by adaptive iteration

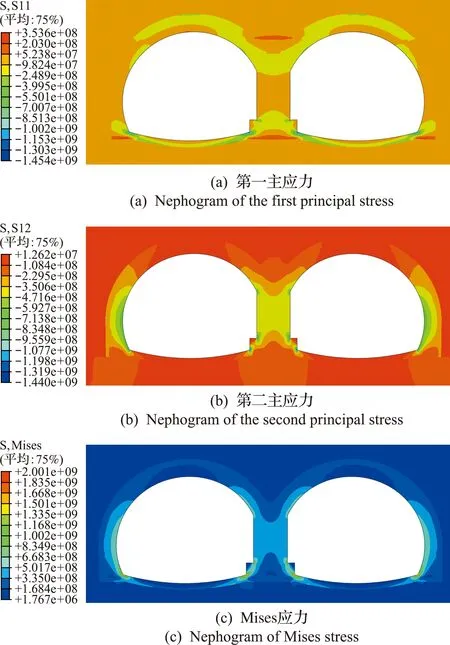
图13 满足精度要求的应力云图Fig.13 Stress nephograms of meeting the given accuracy

从上述算例的数值试验结果可知,本文所编全流程Python脚本对求解含有凹角或孔洞的非光滑物理区域、材料常数不连续和应力集中等问题都是非常有效的。按照不限区域方式实施自适应网格重划,对处理实际问题也是非常方便,均能在奇性解附近自动加密网格,进一步验证了算法的有效性和Python脚本的适应性。另外,对多介质问题,还可以对每一种介质单独设置自适应网格重划方式及选取不同的误差控制标准,应用灵活方便。在Python脚本中,可直接添加新模型以及修改相关参数,从而方便地实现对不同问题的自适应有限元计算或模拟。

4 结 论

自适应有限元法是求解含有凹角或孔洞等的非光滑物理区域、材料常数不连续和应力集中等实际工程问题的有效数值方法之一。在利用Abaqus进行自适应网格重划与模拟时,若创建的模型复杂或存在大量重复操作时,二次开发则更具优势。本文目的是将已有的网格重划分算法与Python脚本有机结合进行二次开发,编写相应的自适应有限元程序,通过直接对Abaqus内核进行操作,可实现从几何建模、网格剖分、定义材料属性、加载和有限元求解到查看计算结果的自动化处理,即实现全流程脚本控制。本文重点分析了误差控制标准的选取对计算结果的影响,并通过几类典型问题验证了Python脚本的适应性及方法的有效性。

本文做了有限的数值试验,当功能强大的Abaqus与Python相结合,其功能将更加强大。本文算例主要考虑的是二维单介质或多介质线弹性问题,相应的自适应网格划分已经非常复杂。而在实际工程应用中,更多的是非线性问题,将自适应网格重划方法扩展到非线性问题意义更大,也更能发挥有限元方法的通用性优势。针对非线性问题的仿真和分析,一方面,需要进一步测试Python脚本的适应性和有效性;另一方面,还需要利用Abaqus提供的其他自适应网格技术,如ALE自适应网格进行Python编程,以提高诸如大变形问题的仿真分析效率。