不同重力场下颗粒冲击过程的离散元分析

于 杰, 罗 枭, 赵婷婷, 张 祺*,3

(1.太原理工大学 机械与运载工程学院,太原 030024;2.太原理工大学 土木工程学院,太原 030024;3.中国科学院 物理研究所,北京 100080)

1 引言

颗粒介质冲击现象在自然界和工业中广泛存在,如风沙运动中的颗粒床碰撞、海滩脚印的形成和月球飞行器的着陆等。在冲击过程中,颗粒床同时表现出固体状态和流体状态并相互演化,此时颗粒介质的力学行为是多重状态的组合,使得颗粒冲击的研究不再是一个简单的问题。对颗粒介质冲击动力学过程及相应力学行为的研究,会加深对颗粒介质冲击相关的复杂自然现象的理解(如陨石撞击星球表面),具有重大的科学意义和广泛的应用背景。在试验方面,Uehara等[1]最早开展了低速浅冲击试验,结果表明冲击深度与冲击颗粒下落的总高度呈1/3次幂律关系。此外,大量试验研究表明冲击物的形状[2]、性质[3]、冲击角度[4]、颗粒床厚度和容器边界[5]等因素均会对冲击物的穿透深度和冲击坑形态产生影响。在模拟方面,Ciamarra等[6]最早进行了二维圆盘冲击模拟并提出了颗粒冲击的三个阶段。Wang等[7]开展了不同冲击角度的二维冲击模拟,结果表明当冲击角度小于临界值(约30°),停止时间随冲击速度线性增加。也有学者就颗粒冲击的力学模型[8]、溅起颗粒动力学[9]和其他方面问题进行研究。如在缓冲性能方面,王嗣强等[10]基于连续函数包络的超二次曲面单元构造了非球形颗粒,结果表明相比具有尖锐顶点和平面的颗粒,表面光滑的球形颗粒具有更好的缓冲效果。上述的研究工作都是在地球重力环境下进行的,在地面上观察到的颗粒介质丰富的运动行为叠加了颗粒自身性质与重力因素的影响,而对于颗粒介质的本征行为还没有得到充分的研究。

在不同重力场中,颗粒介质会表现出不同的特性。如Wang等[11]在零重力环境双室颗粒气体系统偏析过程的数值模拟表明,零重力环境中的偏析与激励强度Γ无关。Peng等[12]采用悬壁筒仓来消除Janssen效应,发现在微重力环境下,重力驱动的Beverloo公式不再适用,可利用孔洞附近的压力替代重力产生颗粒流动。在颗粒冲击方面,Colwell等[13]的微重力冲击实验表明喷射物锥角的速度和冲击物的能量呈1/2次的幂律关系。Altshuler等[14]进行了不同重力加速度下静止物体侵入颗粒介质动力学的系统试验和模拟,发现静止在颗粒床上的物体的最终穿透深度与重力加速度无关。Ji等[15]通过数值模拟发现,在月球重力下,着陆器的冲击力峰值和穿透深度随其速度和质量的增加而增大。此外,也有学者对微重力下的颗粒冲击成坑过程[16]进行了研究。总体来说,对微重力下颗粒介质行为的研究刚刚起步,且对冲击物运动特征的研究还较少。

目前常见的实现微重力环境的技术有落塔、抛物线飞机和失重火箭等,但构建微重力环境消耗巨大,且持续时间较短。离散元法是研究颗粒介质[17]和岩土工程[18]的一种成熟手段,利用离散元法控制重力加速度的变化,可以弥补实验技术手段的不足。所以,本文采用离散元方法(DEM)建立颗粒床在球体冲击物作用下的数值模型,在不同重力加速度条件下,对颗粒冲击过程进行数值计算,探究重力加速度对颗粒冲击过程的影响,揭示不同重力加速度下冲击物的运动特征变化。

2 颗粒介质冲击过程的离散元模型

2.1 颗粒间的非线性接触模型

采用球体颗粒单元及其非线性接触模型计算颗粒间的相互作用力,对颗粒介质的冲击过程进行数值模拟。

表1 颗粒的接触模型Tab.1 Contact force model of particles

对于多分散颗粒系统,离散元模拟的时间步长应小于瑞利波传播最小颗粒半球面需要的时间,可取为

(1)

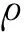
2.2 颗粒介质冲击过程的离散元模型与试验对比

为验证离散元模型的有效性,对颗粒层厚度为H1的球体冲击缓冲过程进行数值模拟,并与季顺迎等[19,20]地球重力下的试验结果和模拟结果进行对比。模拟计算和真实试验设置的条件一致,令冲击物的直径D=5 cm,圆筒容器高度H2=30 cm,颗粒单元在圆筒中随机生成,颗粒总数由颗粒厚度H1决定,所有颗粒在重力作用下达到稳定平衡状态。在离散元计算中颗粒单元的直径在[4.0 mm,5.0 mm]内随机分布,其均值为4.5 mm。球形冲击物直径为D,初速度为v0,其质心位置距颗粒层表面的高度为H3,颗粒介质冲击的离散元模型如图1所示。本文离散元模拟使用的主要计算参数列入表2。

图1 H1=0.5 cm时,冲击力变化过程的试验结果[19]和模拟结果[20]与本文离散元计算值对比Fig.1 Experimental results[19] and simulation results[20] of the impact force for H1=0.5 cm compared with the simulation results of this paper

图1所示为当颗粒厚度为H1=0.5 cm时,模拟计算得到的底板冲击力时程曲线。当颗粒厚度H1=0.5 cm时,模拟计算得到的底板冲击力峰值和冲击力持续时间都与试验结果大致相同。离散元模拟得到底板冲击力结果较为稳定,而试验结果的波动现象较为明显。这是由于在试验测量中,圆筒的底板产生了一定的振动,因此出现了较为明显的波动现象,而在本文的离散元模拟中,底板设置为刚性板,导致底板受到的冲击力震荡幅度不明显。如图2所示,季顺迎的试验结果[19]和模拟结果[20]与本文离散元模拟结果得到的底板冲击力峰值的变化趋势是相同的,呈现随颗粒厚度的增加底板冲击力峰值从大变小并趋于稳定的过程。综上所述,虽然离散元计算结果与试验值在数值上有一定的差距,但其在冲击力随颗粒厚度的变化趋势上是一致的,表明本文使用的离散元模型可以合理地模拟地球重力环境下颗粒冲击过程。

图2 不同颗粒厚度下试验结果[19]和模拟结果[20]与本文离散元计算获得的底板最大冲击力Fig.2 Experimental results[19] and simulation results[20] compared with the maximum impact loads obtained from the discrete element calculations under various granular thicknesses

3 不同重力加速度下颗粒介质的冲击过程

在上述模型的基础上进一步探究不同重力加速度对颗粒介质冲击过程的影响。为了减少边界对冲击过程的影响,设置冲击物的直径为0.026 m,圆筒直径为0.38 m,颗粒数量为2×105个,冲击颗粒距离床的初始高度小于1×10-6m,其他参数均使用表2的数值。在圆筒容器中随机生成颗粒并给予其一定的初始速度,颗粒系统在重力的作用下达到平衡状态。同时,为了避免模拟试验的随机性,在各组重力加速度下给予颗粒不同的初速度来构建3种不同的颗粒床,对不同冲击速度的冲击结果进行统计平均。

3.1 冲击物的穿透深度

图3所示为重力加速度等于5.49 m/s2时,不同冲击速度下冲击物垂直方向的位移z随时间的变化曲线。其中,将颗粒床的初始表面高度设置为坐标零点,向下为正方向。可以看出,冲击物在接触颗粒床后迅速减速,之后冲击物逐渐穿透颗粒床,最终冲击物会停留在一个固定的深度,将冲击物最底点到颗粒床表面的距离定义为穿透深度d。当冲击物的垂直速度第一次减少到零后,虽然飞溅的颗粒会碰撞到冲击物,但冲击物的垂直位移的变化非常微小。定义冲击物与床面接触瞬间到垂直速度首次为零瞬间为持续碰撞时间tc。随着冲击速度的增大,冲击物的穿透深度d增大,而当冲击速度大于5 m/s后,持续碰撞时间是一个固定的值。不同重力下颗粒介质的冲击过程同地球重力下的结果类似[6],可分为3个阶段,如图4所示(从左至右重力加速度分别为1.64 m/s2,5.49 m/s2和9.81 m/s2),第一阶段为冲击阶段,颗粒冲击物接触颗粒床,颗粒床压缩同时只有少量颗粒弹出,不同重力加速度下的穿透深度和弹出颗粒大致相同,说明重力加速度对冲击阶段的影响较小;第二阶段为穿透阶段,颗粒冲击物持续穿透颗粒床,同时,冲击物在阻力作用下速度减小到0 m/s;第三阶段为坍塌阶段,颗粒床在重力作用下坍塌,最终形成稳定的冲击坑形貌。

图3 在5.49 m/s2重力加速度下,不同冲击速度下颗粒冲击物位移随时间的变化曲线Fig.3 Curves of impactor displacement versus time for different impact velocities at 5.49 m/s2 gravitational acceleration

图4 v0=15 m/s时,不同阶段的颗粒床切片图Fig.4 Slice of the particle bed at different stages at v0=15 m/s

图5 冲击物的最终穿透深度随重力加速度和冲击速度的变化,内插图为系数α和β随重力加速度的变化Fig.5 Penetration depth of the impactor varies with the accelera-tion of gravity and the impact velocity,the inset shows the varia-tion of the coefficients α and β with the acceleration of gravity

图6 颗粒冲击物的穿透深度随总下降高度的变化(插图分别为冲击速度10 m/s下,重力加速度为1.638 m/s2和11.4777 m/s2的颗粒床稳定后的冲击坑形态的切片图)Fig.6 Variation of penetration depth of the particle impactor with total drop height(Insets show the stabilised impact crater morpho-logy of the particles at impact velocities of 10 m/s and gravita-tional accelerations of 1.638 m/s2 and 11.4777 m/s2 respectively)

3.2 冲击物的减速穿透过程

图7所示为冲击速度v0=5 m/s时,不同重力加速度条件下冲击物的速度随位移的变化,为了避免颗粒床构型的影响,本文采用同一种颗粒床构型。如图8所示,冲击物的减速穿透过程分为两个阶段,第一阶段为冲击物位移小于冲击物半径R时,冲击物剧烈减速至大约冲击速度的27%(主要受颗粒床构型影响)左右,重力加速度对此阶段无影响;第二阶段为冲击物位移大于冲击物半径R时,冲击物速度减小得较为缓慢,冲击物随着穿透深度的加深,速度逐渐减小到零,并且重力加速度越小,冲击物的速度减少越缓慢,穿透深度越深。造成这个现象的原因有两种,一是Brzinski等[22]提出的对于球形冲击物,必须根据冲击物位移z是否大于冲击物半径R来考虑摩擦力的形式,即摩擦力与冲击物横截面面积成正比,当冲击物位移大于冲击物半径时,横截面面积恒定;二是归因于从惯性阻力状态向摩擦阻力状态的转变[21],即随着穿透的进行,超过一定的穿透深度时,准静态穿透阻力超过动态阻力。对于减速穿透过程,重力加速度对冲击过程的影响表现在冲击物穿透深度大于冲击物直径的阶段。

图7 冲击速度为5 m/s时,冲击物速度随冲击物位移的变化Fig.7 Variation of impactor velocity with impactor displacement at impact velocity of 5 m/s

图8 持续碰撞时间tc随冲击速度和重力加速度的变化(插图为t0和重力加速度的拟合)Fig.8 Variation of sustained collision time tc with impact velocity and gravitational acceleration (Inset shows the fit of t0 and gravitational acceleration)

3.3 持续碰撞时间

4 结 论

本文用离散元方法对颗粒介质冲击过程进行了数值分析,通过与球体冲击的试验结果进行对比验证,表明当前离散元方法适用于模拟颗粒介质的冲击过程。在此基础之上,进一步研究了不同冲击速度和不同重力加速度对冲击物运动特征的影响,主要结论如下。

(1) 在所有重力加速度下,冲击物的穿透深度d与冲击速度v0的关系可以用Poncelet模型表达,重力加速度越低,重力的约束效果越弱,颗粒床的惯性应力和粘性阻力系数越小。d与冲击物下落的总高度H表现为d～Hn的幂律关系,当H<10 m时,d与H的幂率标度为0.322,而H>10 m时,d与H的幂率标度下降到0.211。

(2) 冲击物的减速穿透过程分为两个阶段,重力加速度对穿透深度小于冲击物半径的范围无影响,此时,由相对速度决定的动态阻力起主要作用。当冲击物穿透深度大于冲击物半径时,重力加速度越小,冲击物减速越慢,穿透深度越深。

(3) 不论重力加速度如何,当冲击速度v0>5 m/s时,冲击物的持续碰撞时间tc与冲击速度v0无关,并且同重力加速度的-1/2次呈正比例关系。